用户: Cybcat/神秘具体问题

1极大安全组

有人询问, 假设在一个 $5\times 5$ 的方格共计 $25$ 个格子中选出一些构成一个子集. 如果满足子集中的格子没有五个在同一行, 没有五个在同一列, 且没有五个在同一条对角线 (左上到右下, 右上到左下, 共两条) 上, 就称这个子集为一个安全组. 那么极大安全组的总数是多少呢? 经过编程运算, 我们得到如下结果:

合计 $4577$ 个极大安全组. 按照不在子集中的格子数量分类:

有 $5$ 个格子未选中的情况有 $48$ 个, 有 $6$ 个格子未选中的情况有 $1216$ 个, 有 $7$ 个格子未选中的情况有 $2432$ 个, 有 $8$ 个格子未选中的情况有 $872$ 个, 有 $9$ 个格子未选中的情况有 $9$ 个.

出于好奇我们也计算了 $4\times 4$ 的情况.

合计 $290$ 个极大安全组. 按照不在子集中的格子数量分类:

有 $4$ 个格子未选中的情况有 $10$ 个, 有 $5$ 个格子未选中的情况有 $112$ 个, 有 $6$ 个格子未选中的情况有 $160$ 个, 有 $7$ 个格子未选中的情况有 $8$ 个.

最后我们具有表格. 它记录了每个安全组中未被选中的格子从二进制转化为十进制的结果. (见页末) (从一个具体十进制数出发, 转化为二进制后补充前导 $0$ 至 $16,25$ 位, 然后按照字典序填入即可)

这个问题是怎么来的呢? 因为最近流行一类叫某某废物 bingo 的游戏, 例如下面这个

是人	这辈子没出过银河系	会呼吸	心率低于 $10^{800}$BPM	身高低于 $90$ 万米
有 DNA	有骨骼	有心肌细胞	有肺泡	有肺动脉
有毛细血管	有左心房	有右心室	有肾小管	有肽链
有羟基	有羧基	有碳原子	有氧原子	有质子
有中子	有电子	有中微子	有胶子	有夸克

或者

认为度量空间中开球闭包是闭球	认为可数的无挠 Abel 群自由	认为仿射簇乘积的 Zariski 拓扑是乘积拓扑	认为拓扑连通分支既是开集也是闭集	认为紧 Hausdorff 空间都可度量化
认为高维 Borel 集的投影仍是 Borel 集	算不清曲线模空间的相交数或者忘记自同构	算不清流形上的 Laplace 算子	认为 Banach 空间的闭子空间具有直和补	认为 Noether 整环 Krull 维数有限
认为几乎处处收敛一定依测度收敛	认为连续可导函数在某点正导数则邻域内单增	认为可导函数的导数连续点总具有正测度或者正 Hausdorff 维数	无法正确默写一般的 Hirzebruch–Riemann–Roch 定理	分不清或记错四个 Jacobi $\theta$ 函数
分不清投射内射, 平坦和忠实平坦对象	无法正确计算较小的球面同伦群	计算 Riemann 曲率度量分不清上下指标或者计算结果差一个正负	认为可分 Banach 空间都有 Schauder 基	算不清楚 $t$-分布的密度函数或高阶矩
算不清射影空间中超曲面的 Hodge 数	无法正确对应 Dynkin 图, 根系和半单李代数	认为矩阵的算子范数是特征值绝对值的最大值	忘记或记错 Sobolev 空间之间相互嵌入的条件	认为可分拓扑空间的子空间可分

然后按照自己个人的情况标记格子, 如果连出一行或者一列或者一条对角线就是废物. 所以我们提出了安全组和极大安全组的概念, 以检查不废物的极端情况应该是什么.

2手机图案密码

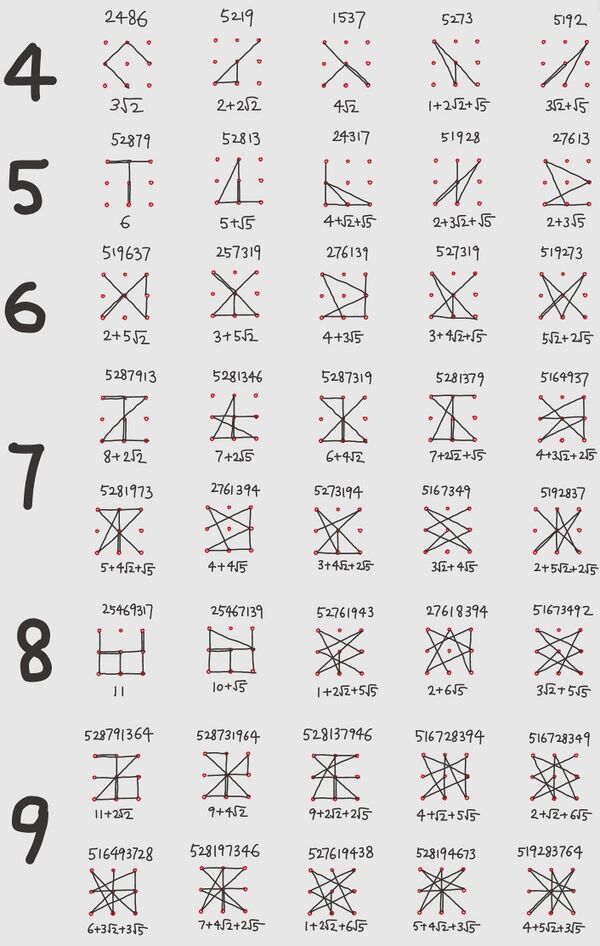
设置手机图案密码需要使用者在 $3\times 3$ 的正方形点阵中连接若干个点 (九个点按照数字键盘的顺序记作 1 到 9), 得到分段线性的路径作为密码. 通过按顺序记录路径所包含线段的端点对应的数字我们可以唯一刻画这条路径. 例如 12639457 对应: 又例如洛书的 492357816 对应(也可以选择按照 $\left[\begin{array}{ccc}4& 9& 2\\ 3& 5& 7\\ 8& 1& 6\end{array}\right]$ 数字从小到大顺序连接格点, 得到的将是上述图案的某种对称)

按照密码要求, 端点序列需要满足下面的三个条件:

•	序列包含的端点至少有四个.
•	序列包含的端点不能重复.
•	某个格点如果在路径上, 那么它必须在第一次被该路径经过时成为端点.

最后一条规则虽然限制了密码, 但是保证了这样记录的密码被路径作为折线唯一决定.

为了解释最后一条规则, 我们展示这样的例子: 46852, 4682 等都是不合法的密码, 而 45682 是合法的密码. 因为 2 第一次被路径经过是在 4 到 6 的线段, 因此端点 5 必须出现在 46 之间. 而后因为端点不能重复的规则, 从 8 到 2 的过程中虽然路径经过了 5 但是它不是端点. 类似地, 54682, 4175382 等都是合法的密码.

好, 那么关于密码的有趣事实我们列举如下:

•	首先, 包含端点数为 $4,5,6,7,8,9$ 的密码数量分别为 $1624,7152,26016,72912,140704,140704$. 不难检查, 一个密码如果合法地经过了八个端点, 它总能合法地抵达第九个. 合法密码的总数量为 $389112$.
•	如果只考虑不含 $0$ 的各数码不重复的 $4,5,6,7,8,9$ 位的正整数, 那么数量分别为 $3024,15120,60480,181440,362880,362880$, 于是合法的密码对应的正整数分别占其中的 $53.7\%,47.3\%,43.0\%,40.2\%,38.8\%,38.8\%$. 总的来说, $985824$ 个正整数中有 $39.5\%$ 是密码.
•	其次, 我们来关心密码的欧氏长度, 这些位数的密码长度所在的区间分别为$$\begin{array}{r}[3,3\sqrt{5}\approx 6.71],[4,4\sqrt{5}\approx 8.94],[5,5\sqrt{2}+2\sqrt{5}\approx 11.54],\\ [6,5\sqrt{2}+3\sqrt{5}\approx 13.78],[7,2+5\sqrt{2}+3\sqrt{5}\approx 15.78],\\ [8,4+5\sqrt{2}+3\sqrt{5}\approx 17.78].\end{array}$$很明显任何密码长度都形如 $a+b\sqrt{2}+c\sqrt{5}$ 其中 $a,b,c$ 都是非负整数, 而且注意到 $1,\sqrt{2},\sqrt{5}$ 在 $\mathbb{Q}$ 线性无关, 所以这个表示方法唯一.
•	最短密码的长度没什么好说的, 各位数的最短的密码分别具有 $80,104,128,112,112,40$ 种可能性. 而最长密码就比较有意思了, 分别只具有 $16,16,8,16,16,8$ 种可能性. ∘首先是长度 $4$ 和 $5$ 的各 $16$ 种都很容易明白, 毕竟 $\sqrt{5}$ 就是沿着 183492761 的顺序或者反过来走, 这样除了 $5$ 以外的八个数开头每个有两种 (顺序). ∘接下来是长度 $6$, 从此长度开始, 最长的密码都从 5 开始, 这可能违反一些人的直觉. 典型例子是 519273, 其他都是其对称, 从角开始, 相邻的角结束, 所以总共有 $8$ 种. 对于长度 $7$, 典型的例子是 5192734,5192738. 很明显就是在 $6$ 的基础上延一个 $\sqrt{5}$. 于是对于 $6$ 的每种情况都对应 $7$ 的两种情况, 所以是 $16$ 种. 展示如下: ∘接下来长度 $8$ 较为复杂, 有两种典型, 51927346, 51928376. 前者是长度 $7$ 者延一个 $2$, 后者则是某种重新排布, 其他情况都是对称, 不难检查共计 $16$ 种. 而长度 $9$ 的则是以 519283764 为典型, 是长度 $8$ 后者再延申 $2$, 其他情况都是对称, 总计 $8$ 种. 展示如下: 值得一提的是, 最长的 $4,5,6,7,8$ (部分 $8$) 都能通过从格点 1 或者 5 出发直接贪心 (每次连接最远的不违反规则的顶点) 得到, 而最长的 $9$ (和部分 $8$) 需要微调. 至于它直观上是不是最长的, 通过比对洛书密码长度是 $2+2\sqrt{2}+4\sqrt{5}\approx 13.77$ 而看起来也很长的 516729438 则是左式的$$\sqrt{2}+7\sqrt{5}\approx 17.07<17.78\approx 4+5\sqrt{2}+3\sqrt{5}.$$ ∘第二长的密码也很有意思, 分别有 $8,16,16,8,16,16$ 个, 长度如下列出$$\begin{array}{rl}3\sqrt{2}+\sqrt{5}\approx 6.48& <6.71\approx 3\sqrt{5}\\ 3\sqrt{2}+2\sqrt{5}\approx 8.71& <8.94\approx 4\sqrt{5}\\ 5\sqrt{5}\approx 11.18& <11.54\approx 5\sqrt{2}+2\sqrt{5}\\ 2+5\sqrt{2}+2\sqrt{5}\approx 13.54& <13.78\approx 5\sqrt{2}+3\sqrt{5}\\ 7\sqrt{5}\approx 15.65& <15.78\approx 2+5\sqrt{2}+3\sqrt{5}\\ 3+4\sqrt{2}+4\sqrt{5}\approx 17.60& <17.78\approx 4+5\sqrt{2}+3\sqrt{5}\end{array}$$对应的 $4,5,7,9$ 位的典型为 5192; 51673, 51927; 5192837; 527381946, 528194376. 只展示 $9$ 位的图像: ∘此外我们还统计了所有给定欧氏距离 $d$ 以及点的数量 $n$ 后, 能在方阵 $D_4$ 对称性下唯一确定的密码, 如下展示: 刚好每个 $n$ 对应的这样 $d$ 的数量都是五的倍数, 所以排列工整.
•	接下来就是长度的统计信息,

目录

	表格 1, 极大安全组按照二进制编码, 转十进制储存.
	Mordell, 搬运了 Helmut Richter 的 Mordell 方程解的表格.