用户: Kokic/正则表达式与矩阵

1起始的物语

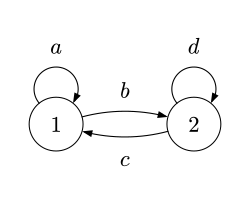
字母表 $\Sigma =\{a,b,c,d\}$ 上具两个状态的自动机

其箭头可写为如下正则表达式

$$\begin{array}{rl}1⟶1& :(a+b{d}^{\ast }c{)}^{\ast }\\ 1⟶2& :(a+b{d}^{\ast }c{)}^{\ast }b{d}^{\ast }\\ 2⟶1& :d^{\ast }c(a+b{d}^{\ast }c{)}^{\ast }\\ 2⟶2& :d^{\ast }+d^{\ast }c(a+b{d}^{\ast }c{)}^{\ast }b{d}^{\ast }\end{array}$$

注 1.1. 右侧的表达式是直观的, 例如 $(a+b{d}^{\ast }c{)}^{\ast }$ 匹配如下字符串

"", "a", "abc", "abdc", "aa", "aabc", "aabdc", ...

详细来说, 即

•	$(a+b{d}^{\ast }c{)}^{\ast }$ 表示匹配空或多次 $a+b{d}^{\ast }c$
•	$a+b{d}^{\ast }c$ 表示匹配 $a$ 或 $b{d}^{\ast }c$
•	$b{d}^{\ast }c$ 表示匹配 $bc$, $bdc$, $bddc$, $\cdots$ ($d$ 零次或多次)

再记 $\alpha =(a+b{d}^{\ast }c{)}^{\ast }$, 因此得到 [1.2]$$A^{\ast }=\left(\begin{array}{cc}\alpha & \alpha b{d}^{\ast }\\ d^{\ast }c\alpha & d^{\ast }+d^{\ast }c\alpha b{d}^{\ast }\end{array}\right)$$

随后, 由于 $A^{-1}=(1-A{)}^{\ast }$, 展开计算得

注 1.2. 此处 $A^{\ast }$ 是沿用了闭包的记号 ${\square }^{\ast }$ 而非指伴随矩阵.

$$\begin{array}{rl}{A}^{-1}& =(1-A{)}^{\ast }\\ & ={\left(\begin{array}{cc}1-a& -b\\ -c& 1-d\end{array}\right)}^{\ast }\\ & =\left(\begin{array}{cc}(1-a+b(1-d{)}^{\ast }c{)}^{\ast }& \cdots \\ \cdots & \cdots \end{array}\right)\\ & =\frac{1}{ad-bc}\left(\begin{array}{cc}d& -b\\ -c& a\end{array}\right)\end{array}$$

这个过程比经典方法更自然. 不仅如此, 对于更大的方阵$$M=\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)\in {\text{Mat}}_{n\times n}(R)$$其中 $n>2$, 这仍然正确.

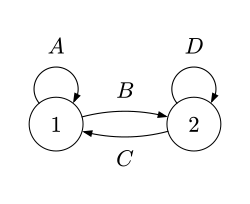
矩阵作为状态间的箭头

相应的记 $Q=(A+B{D}^{\ast }C{)}^{\ast }$, 有$$M^{\ast }=\left(\begin{array}{cc}Q& QB{D}^{\ast }\\ D^{\ast }CQ& D^{\ast }+D^{\ast }CQB{D}^{\ast }\end{array}\right)$$

可以正确地求得 $M^{-1}$.

2定义

Kleene 代数的一个重要例子是所谓的正则语言集 ${\text{Reg}}_{\Sigma }$, 固定有限字母表 $\Sigma$, 可定义如下

•	空集 $\varnothing$ 是正则语言 (加法单位).
•	只包含空字符串的集合 $\{ϵ\}$ 是正则语言 (乘法单位).
•	对于 $a\in \Sigma$, $\{a\}$ 是正则语言.
•	对于正则语言 $A$, $B$. $A\cup B$, $A{\times }_{\Sigma }B$ 和 $A^{\ast }$ 是正则语言.
•	$\Sigma$ 上不存在其它正则语言.

这里 $A{\times }_{\Sigma }B$ 基本就是 $A\times B=\{(a,b):a\in A,b\in B\}$, 但将配对 $(a,b)$ 视为字符串拼接 $ab$. 闭包 $A^{\ast }$ 定义为满足如下性质的最小集合.

•	匹配空. 即 $ϵ\in A^{\ast }$.
•	对拼接封闭. 即 $A{\times }_{\Sigma }A{\times }_{\Sigma }\cdots {\times }_{\Sigma }A\subset A^{\ast }$.

现在定义 Kleene 代数 $(K,+,\times ,{\square }^{\ast },0,1)$. 一言以蔽之, Kleene 代数即为半环 $(K,+,\times )$ 且有偏序结构 [2.1] $(K,\le )$ 并带上 Kleene 星运算 ${\square }^{\ast }$, Kleene 星运算或曰字符闭包满足如下闭包公理

$$\begin{array}{c}\forall a\in K,1+a{a}^{\ast }\le a^{\ast }\\ \forall a\in K,1+a^{\ast }a\le a^{\ast }\\ \forall a,x\in K\text{s.t.}ax\le x⟹a^{\ast }x\le x\\ \forall a,x\in K\text{s.t.}xa\le x⟹x{a}^{\ast }\le x\end{array}$$

注 2.1. 依通常定义, 即 $a\le b⟺\exists x\in K,a+x=b$.

我们重新指出, 给定有限字母表 $\Sigma$, 六元组 $({\text{Reg}}_{\Sigma },\cup ,{\times }_{\Sigma },{\square }^{\ast },\varnothing ,\{ϵ\})$ 构成 Kleene 代数.

回顾 起始的物语, 其正是如下事实的冰山一角

命题 2.2. Kleene 代数上的方阵与矩阵运算连同字符闭包运算一起构成另一个 Kleene 代数.

$$\begin{array}{c}{\text{Mat}}_{n\times n}(K)\text{over}(K,{+}_K,{\times }_K,{\square }_K^{\ast },0_K,1_K)\\ \Downarrow \\ ({\text{Mat}}_{n\times n}(K),+,\times ,{\square }^{\ast },0,1)\end{array}$$

3例子

对于 $M=\left(\begin{array}{ccc}1& 0& 0\\ 3& 9& 1\\ 7& 2& 9\end{array}\right)$, 现在来计算 $M^{-1}$. 首先算出$$1-M=\left(\begin{array}{ccc}0& 0& 0\\ -3& -8& -1\\ -7& -2& -8\end{array}\right)$$将其分解成$$A=\left(\begin{array}{c}0\end{array}\right),B=\left(\begin{array}{cc}0& 0\end{array}\right),C=\left(\begin{array}{c}-3\\ -7\end{array}\right),D=\left(\begin{array}{cc}-8& -1\\ -2& -8\end{array}\right)$$

立即计算出 $D^{\ast }=\left(\begin{array}{cc}-\frac{9}{79}& -\frac{1}{79}\\ & \\ -\frac{2}{79}& \frac{9}{79}\end{array}\right)$, $Q=(A+B{D}^{\ast }C{)}^{\ast }=((0)+(0){)}^{\ast }=(1)$, 其他部分类似. 最后可以得到$$M^{-1}=\left(\begin{array}{ccc}1& 0& 0\\ & & \\ -\frac{20}{79}& \frac{9}{79}& -\frac{1}{79}\\ & & \\ -\frac{57}{79}& -\frac{2}{79}& \frac{9}{79}\end{array}\right)$$