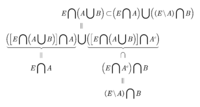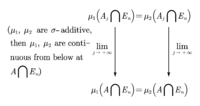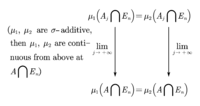4. Caratheodory theorem

(待修改! ) Given a semi-algebra $S \subset ℑ (Ω)$ over $Ω$ and an additive function $μ : S ⟶$ $R_{+}$ $\cup {+ \infty}$ , we prove that there exist a unique extension $ν : A (S) ⟶ R_{+} \cup {+ \infty}$ which is additive in the last note. In this note, our goal is that prove the following fact $σ -additive μ : S ⟶ R_{+} \cup {+ \infty} ⇓ ↓ extension σ -additive ν : A (S) ⟶ R_{+} \cup {+ \infty} ⇓ ↓ extension σ -additive π : F (A) ⟶ R_{+} \cup {+ \infty}$

##### Step 1

Definition

Given an algebra $A \subset ℑ (Ω)$ over $Ω$ and a function $ν : A ⟶ R_{+} \cup {+ \infty}$ , we define $π * : ℑ (Ω) A ⟶ R + \cup + \infty \mapsto E i \in A i ⩾ 1 c o v e r A i n f i ⩾ 1 \sum ν (E i ) $ Definition

Given $C \subset ℑ (Ω)$ where $C$ contain the empty set $\emptyset$ and we say a function $μ : C ⟶ R_{+} \cup {+ \infty}$ is an outer measure on $C$ if

- $μ (\emptyset) = 0$ - $E \subset F$ and $E$ , $F \in C$ $⟹$ $μ (E) ⩽ μ (F)$ - $E \in C$ and ${E_{i} \in C}_{i ⩾ 1} cover E$ $⟹$ $μ (E) ⩽ \sum_{i ⩾ 1} μ (E_{i})$

Claim

$π^{*}$ is an outer measure.

- Take ${E_{i} = \emptyset}_{i ⩾ 1}$ , then

$π * (\emptyset) ⩽ b y d e f . i ⩾ 1 \sum ν (E i ) = i ⩾ 1 \sum ν (\emptyset) = 0 $

Therefore $π^{*} (\emptyset) = 0$ since the codomain of $π^{*}$ is nonnegative.

- Let $E \subset F$ and ${F_{i} \in A}_{i ⩾ 1} cover F$ , it is clear that ${F_{i} \in A}_{i ⩾ 1} cover E$ . Set $F = {{F_{i} \in A}_{i ⩾ 1} ∣ ∣ ∣ {F_{i} \in A}_{i ⩾ 1}$ $cover F}$ and $E = {{E_{i} \in A}_{i ⩾ 1} ∣ ∣ ∣ {E_{i} \in A}$ $_{i ⩾ 1}$ $cover E}$ . It is clear that $F \subset E$ , then

$π * (E) = E i \in A i ⩾ 1 \in E i n f i ⩾ 1 \sum ν (E i ) ⩽ F i \in A i ⩾ 1 \in F i n f i ⩾ 1 \sum ν (F i ) = π * (F) $

- Take a sequence ${E_{i} \in C}_{i ⩾ 1} cover E$ , we assume that $π^{*} (E_{i}) < + \infty$ for all $i$ (note that if $π^{*} (E_{i}) = + \infty$ for some $i$ , then the inequality holds trivially), $π^{*} (E_{i}) = {H_{k} \in A}_{k ⩾ 1} cover E_{i} inf \sum_{k ⩾ 1} ν (H_{k}) < + \infty$ . Fix $ϵ > 0$ , there always exist a sequence ${H_{i, k} \in A}_{i, k ⩾ 1} cover E_{i}$ such that

$π^{*} (E_{i}) ⩽ i ⩾ 1 \sum ν (H_{i, k}) ⩽ π^{*} (E_{i}) + \frac{ϵ}{2 ^{i}}$

Also, ${H_{i, k} \in A}_{i, k ⩾ 1} cover E$ since ${E_{i}} cover E$ . Then $π * (E) ⩽ i, k \sum ν (H i, k ) ⩽ i ⩾ 1 \sum (π * (E i ) + 2 i ϵ ) ⩽ i ⩾ 1 \sum π * (E i ) + ϵ $ holds for any $ϵ > 0$ . So $π^{*} (E) ⩽ \sum_{i ⩾ 1} π^{*} (E_{i})$ .

##### Step 2

We define a family of subsets $M \subset ℑ (Ω)$ , $A \in M$ if $\forall$ $E \in Ω$ satisfy $π^{*} (E) = π^{*} (E ⋂ A) + π^{*} (E ⋂ A^{c})$ We claim that

- $A \subset M$

- $M$ is a $σ$ -algebra

Observation $π^{*} (E) ⩽ π^{*} (E ⋂ A) + π^{*} (E ⋂ A^{c})$ since $E \subset (E ⋂ A) ⋃ (E ⋂ A^{c})$ .

So, if we want to prove that $A \in M$ where $A \in A$ , it sufficient to show that $π^{*} (E) ⩾ π^{*} (E ⋂ A) + π^{*} (E ⋂ A^{c})$ for $\forall$ $E \in Ω$ . Not loss the generality, we may assume that $π^{*} (E) < + \infty$ since the inequality holds trivially while $π^{*} (E) = + \infty$ . Given $ϵ > 0$ , we can find ${E_{i} \in A}_{j ⩾ 1} cover E$ such that

$π^{*} (E) ⩽ i ⩾ 1 \sum ν (E_{i}) ⩽ π^{*} (E) + ϵ$ We obtain $π^{*} (E ⋂ A) ⩽ i ⩾ 1 \sum ν (E_{j} ⋂ A)$ since $E_{i} ⋂ A \in A$ and $E ⋂ A \subset ⋃_{i ⩾ 1} (E_{i} ⋂ A)$ . Similarly, we obtain $π^{*} (E ⋂ A^{c}) ⩽ i ⩾ 1 \sum ν (E_{j} ⋂ A^{c})$ Therefore, $π * (E ⋂ A) + π * (E ⋂ A c) ⩽ i ⩾ 1 \sum (ν (E i ⋂ A) + ν (E i ⋂ A c)) = i ⩾ 1 \sum ν (E j ) ⩽ π * (E) + ϵ $ holds for any $ϵ > 0$ . So we have $π^{*} (E) ⩾ π^{*} (E ⋂ A) + π^{*} (E ⋂ A^{c})$ and hence $A \subset M$ . It is clear that $Ω \in M$ since $π^{*} (E) = π^{*} (E) + π^{*} (\emptyset) =$ $π^{*} (E ⋂ Ω) +$ $π^{*} (E ⋂ Ω^{c})$ .

Assume that $A \in M$ , then (by the definition of $M$ ) we have $π^{*} (E) =$ $π^{*} (E ⋂ A) + π^{*} (E ⋂ A^{c})$ holds for every $E$ . By the symmetry of $A$ and $A^{c}$ , $A^{c} \in M$ .

Given $(A_{j})_{j ⩾ 1} \in M$ , we need to show that $(A_{j})_{j ⩾ 1} \in M$ $⟹$ $⋃_{j ⩾ 1} A_{j} \in M$ .

Remark The property $(A_{j})_{j ⩾ 1}$ $\in M$ $⟹$ $⋂_{j ⩾ 1} A_{j} \in M$ is equal to $(A_{j})_{j ⩾ 1}$ $\in$ $M$ $⟹$ $⋃_{j ⩾ 1} A_{j} \in M$ .

First, we show that $A$ , $B \in M$ $⟹$ $A ⋃ B \in M$ . It sufficient to show the in-equality $π^{*} (E) ⩾ π^{*} (E ⋂ (A ⋃ B)) + π^{*} (E ⋂ (A ⋃ B)^{c})$ holds for $\forall$ $E \in Ω$ . Since $A$ , $B \in M$ , we have $π^{*} (E) = π^{*} (E ⋂ A) + π^{*} (E \ A)$ and $π^{*} (E \ A) = π^{*} ((E \ A) ⋂ B) + π^{*} ((E \ A) \ B)$ Take the second formula into the first one we obtain $π∗(E)=π∗(E⋂A)+π∗((E\A)⋂B)+π∗((E\A)\B)=π∗(E⋂A)+π∗((E\A)⋂B)+π∗(E\(A⋃B))=π∗(E⋂A)+π∗((E\A)⋂B)+π∗(E⋂(A⋃B)c)$ Then it sufficient to show that $π^{*} (E ⋂ A) + π^{*} ((E \ A) ⋂ B) ⩾ π^{*} (E ⋂ (A ⋃ B))$ By the property of $π^{*}$ , it sufficient to show that $E ⋂ (A ⋃ B) \subset (E ⋂ A) ⋃ ((E \ A) ⋂ B)$ Actually,

Next, we show that $M$ is closed by countable union (i.e. $A_{j} \in M$ $⟹$ $A$ $=$ $⋃_{j ⩾ 1} A_{j} \in M$ ).

It sufficient to show the following inequality $π^{*} (E) ⩾ π^{*} (E ⋂ A) + π^{*} (E \ A)$ But we know that $M$ is closed by finite union $π * (E) = π * (E ⋂ (j = 1 ⋃ n A j )) + π * (E \A ⋃ E \j = 1 ⋃ n A j ) ⩾ π * (E ⋂ (j = 1 ⋃ n A j )) + π * (E \A) $ We take $F1F2Fn=A1=A2\A1⋮=An\(A1⋃⋯⋃An−1)$ Then $⋃_{j = 1}^{n} A_{j} = ⋃_{j = 1}^{n} F_{j}$ and it is clear that $F_{j} ⋂ F_{k} = \emptyset$ for any $j$ and $k$ where $j \neq = k$ and $Fj(M is closed by ( )c and finite union)=Aj\(A1⋃⋯⋃Aj−1)=Aj⋂(A1⋃⋯⋃Aj−1)c∈M$ Therefore, $π^{*} (E) ⩾ π^{*} (E ⋂ j = 1 \sum n F_{j}) + π^{*} (E \ A)$ Claim $π^{*} (E ⋂ j = 1 \sum n F_{j}) = j = 1 \sum n π^{*} (E ⋂ F_{j})$ By induction

$1 ⟩$ $n = 1$ , the equality holds trivially

$2 ⟩$ Assume that the equality holds for $n > 1$

$3 ⟩$ for $n + 1$ , we have $π * (E ⋂ j = 1 \sum n + 1 F j ) = π * ((E ⋂ j = 1 \sum n + 1 F j ) ⋂ F n + 1 ) + π * ((E ⋂ j = 1 \sum n + 1 F j ) ⋂ F n + 1 c ) = π * (E ⋂ F n + 1 ) + π * (E ⋂ j = 1 \sum n F j ) = π * (E ⋂ F n + 1 ) + j = 1 \sum n π * (E ⋂ F j ) = j = 1 \sum n + 1 π * (E ⋂ F j ) $

We rewrite the inequality $π^{*} (E) ⩾ π^{*} (E ⋂ \sum_{j = 1}^{n} F_{j}) + π^{*} (E \ A)$ to $π^{*} (E) ⩾ j = 1 \sum n π^{*} (E ⋂ F_{j}) + π^{*} (E \ A)$

$π^{*} (E) ⩾ j ⩾ 1 \sum π^{*} (E ⋂ F_{j}) + π^{*} (E \ A)$

Since the inequality is correct for any $n$ , the following inequality can be hold. Therefore, $π * (E) (b y t h e p r o p e r t y o f π *) ⩾ j ⩾ 1 \sum π * (E ⋂ F j ) + π * (E \A) ⩾ π * (E ⋂ (j ⩾ 1 ⋃ F j )) + π * (E \A) = π * (E ⋂ A) + π * (E \A) $ It completed the proof that $M$ is a $σ$ -algebra.

We now know that

- $A \subset M$ - $M$ is a $σ$ -algebra

Then we obtain the fact $F (A) \subset M$ .

##### Step 3

The restriction $π^{*} ∣_{M} : M ⟶ R_{+} \cup {+ \infty}$ is a extension of $ν$ which define on the algebra $A$ and is $σ$ -additive.

- $π^{*} (A) ⩽ ν (A)$ where $A \in A$

Set ${E_{j}}_{j ⩾ 1} = {A, \emptyset, \emptyset, . . .} cover A$ , then $π^{*} (A) ⩽ \sum_{j ⩾ 1} ν (E_{j}) = ν (A)$ .

- $ν (A) ⩽ \sum_{j ⩾ 1} ν (E_{j})$ where ${E_{j} \in A}_{j ⩾ 1} cover A$ and $A \in A$

We take $F1F2Fn=E1=E2\E1⋮=En\(E1⋃⋯⋃En−1)$ It is clear that $(F_{j})_{j ⩾ 1} \in A$ and $⋃_{j ⩾ 1} F_{j} = ⋃_{j ⩾ 1} E_{j}$ , $F_{j} ⋂ F_{k} = \emptyset$ for any $j$ and $k$ where $j \neq = k$ . Therefore, ${F_{j} \in A}_{j ⩾ 1} cover A$ . We conclude $ν (A) (ν i s σ - a d d i t i v e) (F j ⋂ A \subset E j ) = ν (j ⩾ 1 \sum F j ⋂ A) = j ⩾ 1 \sum ν (F j ⋂ A) ⩽ j ⩾ 1 \sum ν (E j ) $ This inequality holds for all covering of $A$ , so $ν (A) ⩽ E j \in A j ⩾ 1 c o v e r A i n f j ⩾ 1 \sum ν (E j ) = π * (A) $

- $π^{*} ∣_{M}$ is $σ$ -additive

Take $(A_{j})_{j ⩾ 1} \in M$ such that $A_{j} ⋂ A_{k} = \emptyset$ for all $j$ and $k$ where $j \neq = k$ . we conclude that $π^{*} (j ⩾ 1 \sum A_{j}) ⩽ j ⩾ 1 \sum π^{*} (A_{j}) (is clear)$ and $π^{*} (j ⩾ 1 \sum A_{j}) ⩾ π^{*} (j = 1 \sum n A_{j}) = j = 1 \sum n π^{*} (A_{j}) (is clear)$ Then we can take $n$ to be $+ \infty$ , and we get the inequality $π^{*} (j ⩾ 1 \sum A_{j}) ⩾ j ⩾ 1 \sum π^{*} (A_{j})$ Consequently, $π^{*} ∣_{M}$ is an extension of $ν$ and is $σ$ -additive.

##### Step 4

**Goal** Given two functions $μ_{1}$ , $μ_{2} : F (A) ⟶ R_{+} \cup {+ \infty}$ such that $μ_{1} ∣_{A} = μ_{2} ∣_{A}$ . If $Ω$ is $σ$ -finite with respect to $μ_{1}$ and $μ_{2}$ , then $μ_{1} = μ_{2}$ .

Remark Given a set $Ω$ , we say that $Ω$ is $σ$ -finite with respect to $ν_{1} ∣_{A} :$ $A ⟶ R_{+} \cup {+ \infty}$ if for any increasing converges sequence ${E_{j} \in A}_{j ⩾ 1} ⟶ Ω$ , $μ_{1} (E_{j}) < + \infty$ for all $j$ .

Definition

Given a set $Ω$ and $G \subset ℑ (Ω)$ , we say that $G$ is a monotone class if

- ${A_{j} \in G}_{j ⩾ 1} ⟶ A$ is an increasing converges sequence $⟹$ $A \in G$ - ${A_{j} \in G}_{j ⩾ 1} ⟶ A$ is an decreasing converges sequence $⟹$ $A \in G$

Assertion If $(G_{α})_{α \in I} \subset ℑ (Ω)$ is a family of monotone classes where $I$ is an index set. Then $⋂_{α \in I} G_{α}$ is a monotone class (is easy to see).

Given a class $C \subset ℑ (Ω)$ , we define $M (C) : = α ⋂ G_{α}, C \subset G_{α} for all α$ and $M (C)$ is the smallest monotone class which contain $C$ .

Remark $M (C) \neq = \emptyset$ since $ℑ (Ω)$ is a monotone class itself ,so this definition make sense.

<a id="lemma">Lemma</a> Given an algebra $A \subset ℑ (Ω)$ , we have the equality $M (A) = F (A)$ Given an increasing converges sequence ${E_{j} \in A}_{j ⩾ 1} ⟶ Ω$ and fix $E_{n}$ , we define $B_{n} : = {E \in F (A) ∣ ∣ ∣ ∣ μ_{1} (E ⋂ E_{n}) = μ_{2} (E ⋂ E_{n})}$ $1 ⟩$ $A \subset B_{n}$

Take an element $A \in A$ , $μ_{1} (A ⋂ E_{n}) = μ_{2} (A ⋂ E_{n})$ since $A ⋂ E_{n} \in A$ .

$2 ⟩$ $B_{n}$ is a monotone class

Given ${A_{j} \in B_{n}}_{j ⩾ 1} ⟶ A$ an increasing converges sequence, then

$A \in F (A)$ since $A = ⋃_{j ⩾ 1} A_{j}$ , then we have $A \in B_{n}$ .

Similarly, Given ${A_{j} \in B_{n}}_{j ⩾ 1} ⟶ A$ an decreasing converges sequence, then

So $B_{n}$ is a monotone class.

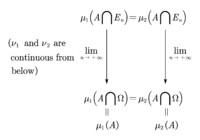
Therefore, $M \subset B_{n}$ . By using [the lemma](#lemma) we have $F (A) \subset B_{n}$ , but, by the construction of $B_{n}$ , $B_{n} \subset F (A)$ . Consequently, $B_{n} = F (A)$ Given $A \in F (A)$ , then $A \in B_{n}$ , we have the following diagram

名字空间

视图

4. Caratheodory theorem