2. Fundamental Groupoid

Path connected component ${\pi }_0$

Definition 2.1. Let $X\in \mathsf{Top}$.

•	A map $\gamma :I\to X$ is called a path from $\gamma (0)$ to $\gamma (1)$.
•	We let ${\gamma }^{-1}$ denote the path from $\gamma (1)$ to $\gamma (0)$ defined by ${\gamma }^{-1}(t)=\gamma (1-t)$.
•	We let $i_{x_0}:I\to X$ denote the constant map to $x_0\in X$.

[h]

Figure 1. A path $\gamma$ in a topological space $X$ and its inverse ${\gamma }^{-1}$

Let us introduce an equivalence relation on $X$ by$$x_0\sim x_1⟺\exists \text{a path from x0 to x1}.$$We denote the quotient space by$${\pi }_0(X)=X/\sim$$which is the set of path connected components of $X$.

Theorem 2.2. ${\pi }_0$ defines a covariant functor from $h\mathsf{Top}$ to $\mathsf{Set}$.

Proof. Exercise.

$\square$

Corollary 2.3. If $X,Y$ are homotopy equivalent, then ${\pi }_0(X)={\pi }_0(Y)$.

Proof. Applying Proposition 1.19 to the functor ${\pi }_0:h\mathsf{Top}\to \mathsf{Set}$.

$\square$

Path category / fundamental groupoid

Definition 2.4. Let $\gamma :I\to X$ be a path. We define the path class of $\gamma$ by$$[\gamma ]=\{\tilde{\gamma }:I\to X|\gamma \simeq \tilde{\gamma }\mathrm{rel}\partial I=\{0,1\}\}.$$

[h]

Figure 2. In a path class, $F:\gamma \simeq \tilde{\gamma }\mathrm{rel}\partial I$

$[\gamma ]$ is the class of all paths that can be continuously deformed to $\gamma$ while fixing the endpoints.

Definition 2.5. Let ${\gamma }_1,{\gamma }_2:I\to X$ such that ${\gamma }_1(1)={\gamma }_2(0)$. We define the composite path$${\gamma }_2\star {\gamma }_1:I\to X$$by$${\gamma }_2\star {\gamma }_1(t)=\{\begin{array}{ll}{\gamma }_1(2t)& 0\le t\le 1/2\\ {\gamma }_2(2t-1)& 1/2\le t\le 1,\end{array}$$

[h]

Figure 3. Composition of paths

Proposition 2.6. Let $f_1,f_2,g_1,g_2$ be paths, such that $f_i(1)=g_i(0)$, $[f_1]=[f_2]$, $[g_1]=[g_2]$. Then $$[g_1\star f_1]=[g_2\star f_2].$$

Proof. We illustrate the proof in the following figure, where $F:f_1\simeq f_2$ and $G:g_1\simeq g_2$.

[h]

$\square$

We conclude that $\star$ is well-defined for path classes$$\begin{array}{c}[g\star f]:=[g]\star [f].\end{array}$$

Proposition 2.7 (Associativity). Let $f,g,h:I\to X$ such that $f(1)=g(0)$ and $g(1)=h(0)$. Then$$\begin{array}{c}([h]\star [g])\star [f]=[h]\star ([g]\star [f]).\end{array}$$

Proof. We illustrate the proof in the following figure:

$\square$

Proposition 2.8 (Identity). Let $\gamma :I\to X$ with endpoints $\gamma (0)=x_0$ and $\gamma (1)=x_1$. Then$$[\gamma ]\star [i_{x_0}]=[\gamma ]=[i_{x_1}]\star [\gamma ].$$

Proof. We only show the first equality, which follows from the figure below: $\square$

Definition 2.9. Let $X\in \mathsf{Top}$. We define a category ${\Pi }_1(X)$ as follows:

•	$\mathrm{Obj}({\Pi }_1(X))=X$.
•	${\mathrm{Hom}}_{{\Pi }_1(X)}(x_0,x_1)$=path classes from $x_0$ to $x_1$.
•	$1_{x_0}=[i_{x_0}]$.

The propositions above imply that ${\Pi }_1(X)$ is a well-defined category. ${\Pi }_1(X)$ is called the path category or fundamental groupoid of $X$.

Groupoid

Definition 2.10. A small category where all morphisms are isomorphisms is called a groupoid. All groupoids form a category $\mathsf{Grpd}$.

Example 2.11. A group $G$ can be regarded as a groupoid $\underline{G}$ with

•	$\mathrm{Obj}(\underline{G})=\{\star \}$ consists of a single object.
•	${\mathrm{Hom}}_{\underline{G}}(\star ,\star )=G$ and composition is given by the group multiplication.

Thus we have a fully faithful functor $\mathsf{Grp}\to \mathsf{Grpd}$.

Recall that ${\gamma }^{-1}$ is the inverse of $\gamma$.

Theorem 2.12. Let $\gamma :I\to X$ with endpoints $\gamma (0)=x_0$ and $\gamma (1)=x_1$. Then$$[\gamma ]\star [{\gamma }^{-1}]=[1_{x_1}],\text{and}[{\gamma }^{-1}]\star [\gamma ]=[1_{x_0}].$$In other words, all morphism in ${\Pi }_1(X)$ are isomorphisms and thus ${\mathbf{\Pi }}_1(\mathbf{X})$ is a groupoid.

Proof. Let ${\gamma }_u:I\to X$ such that ${\gamma }_u(t)=\gamma (tu)$, for any $u\in I$. The following figure gives the homotopy ${\gamma }^{-1}\star \gamma \simeq 1_{x_0}$:

$\square$

Exercise 2.13. Use the following figure to give another homotopy ${\gamma }^{-1}\star \gamma \simeq 1_{x_0}$ for Theorem  2.12.

Let $\mathcal{C}$ be a groupoid, and define the set$${\Pi }_0(\mathcal{C})=\mathrm{Obj}(\mathcal{C})/\sim ,$$where $A\sim B$ if and only if $\exists f:A\to B$ in $\mathcal{C}$. We can view ${\Pi }_0(\mathcal{C})$ as a (discrete) category whose objects are its elements with only identity morphisms. Then $\mathcal{C}\to {\Pi }_0(\mathcal{C})$ defines a functor from $\mathsf{Grpd}$ to $\mathsf{Set}$ (the analogue of path connected components). We say $\mathcal{C}$ is path connected if ${\Pi }_0(\mathcal{C})$ is a single point.

Proposition 2.14. $X$ is path connected if and only if ${\Pi }_1(X)$ is path connected.

Proof. Exercise.

$\square$

Definition 2.15. Let $\mathcal{C}$ be a groupoid. We define the automorphism group of an object $A\in \mathrm{Obj}(\mathcal{C})$ to be$${\mathrm{Aut}}_{\mathcal{C}}(A):={\mathrm{Hom}}_{\mathcal{C}}(A,A).$$Note that this indeed forms a group.

For any $f:A\to B$, it induces a group isomorphism$$\begin{array}{rl}{\mathrm{Ad}}_f:{\mathrm{Aut}}_{\mathcal{C}}(A)& \to {\mathrm{Aut}}_{\mathcal{C}}(B)\\ g& \to f\circ g\circ f^{-1}.\end{array}$$In terms of diagrams,

This naturally defines a functor$$\begin{array}{rl}\mathcal{C}& \to \mathsf{Grp}\text{by assigning}A\mapsto {\mathrm{Aut}}_{\mathcal{C}}(A),f\mapsto {\mathrm{Ad}}_f.\end{array}$$Specialize this to topological spaces, we find a functor$$\begin{array}{c}{\Pi }_1(X)\to \mathsf{Grp}.\end{array}$$

Definition 2.16. Let $x_0\in X$, the group$${\pi }_1(X,x_0):={\mathrm{Aut}}_{{\Pi }_1(X)}(x_0)$$is called the fundamental group of the pointed space $(X,x_0)$.

Theorem 2.17. Let $X$ be path connected. Then for any $x_0,x_1\in X$, we have a group isomorphism$${\pi }_1(X,x_0)\cong {\pi }_1(X,x_1).$$

Proof. Consider the functor ${\Pi }_1(X)\to \mathsf{Grp}$ described above. Since $X$ is path connected and ${\Pi }_1(X)$ is a groupoid, any two points $x_0$ and $x_1$ are isomorphic in ${\Pi }_1(X)$. By Proposition 1.19, ${\pi }_1(X,x_0)\cong {\pi }_1(X,x_1)$.

$\square$

In the path connected case, we sometimes simply denote by ${\pi }_1(X)$ the fundamental group of $X$ without mentioning the reference point via the understanding of Theorem 2.17.

Let $f:X\to Y$ be a continuous map. It defines a functor$$\begin{array}{rl}{\Pi }_1(f):{\Pi }_1(X)& \to {\Pi }_1(Y)\text{by assigning}x\mapsto f(x),[\gamma ]\mapsto [f\circ \gamma ].\end{array}$$

Proposition 2.18. ${\Pi }_1$ defines a functor$${\Pi }_1:\mathsf{Top}\to \mathsf{Grpd},$$that sends $X$ to ${\Pi }_1(X)$.

Proof. Exercise.

$\square$

Proposition 2.19. Let $f,g:X\to Y$ be maps which are homotopic by $F:X\times I\to Y$. Let us define path classes$${\tau }_x=[F{|}_{x\times I}]\in {\mathrm{Hom}}_{{\Pi }_1(Y)}(f(x),g(x)),x\in X$$as illustrated in the figure below:Then ${\tau }_F:=\{{\tau }_x:x\in X\}$ defines a natural transformation$${\tau }_F:{\Pi }_1(f)⟹{\Pi }_1(g).$$

Proof. Let $r:I\to X$ with $r(0)=x_0$ and $r(1)=x_1$. We need to show that the following diagram is commutative at the level of path classes:The composition $F\circ (r\times I)$ gives the following homotopy:which implies $[g\circ r]\star [{\tau }_{x_0}]=[{\tau }_{x_1}]\star [f\circ r]$ as required.

$\square$

This proposition can be summarized by the following diagram.The next theorem is a formal consequence of the above proposition

Theorem 2.20. Let $f:X\to Y$ be a homotopy equivalence. Then$${\Pi }_1(f):{\Pi }_1(X)\to {\Pi }_1(Y)$$is an equivalence of categories. In particular, it induces a group isomorphism$${\pi }_1(X,x_0)\cong {\pi }_1(Y,f(x_0)).$$

Proof. Let $g:Y\to X$ represent the inverse of $f$ in $h\mathsf{Top}$. Applying ${\Pi }_1$ to the homotopy $f\circ g\simeq 1_Y$ and $g\circ f\simeq 1_X$, we find natural transformations from ${\Pi }_1(f)\circ {\Pi }_1(g)$ and ${\Pi }_1(g)\circ {\Pi }_1(f)$ to identity functors. These natural transformations must be natural isomorphisms since ${\Pi }_1(X)$ and ${\Pi }_1(Y)$ are groupoids. Thus the first statement follows. The second statement follows from Proposition 1.26.

$\square$

Proposition 2.21. Let $X,Y\in \mathsf{Top}$. Then we have a canonical isomorphism of categories$${\Pi }_1(X\times Y)\cong {\Pi }_1(X)\times {\Pi }_1(Y).$$In particular, for any $x_0\in X,y_0\in Y$, we have a group isomorphism$${\pi }_1(X\times Y,x_0\times y_0)\cong {\pi }_1(X,x_0)\times {\pi }_1(Y,y_0).$$

Proof. Exercise.

$\square$

Example 2.22. For a point $X=\text{pt}$, ${\pi }_1(\text{pt})=0$ is trivial. It it not hard to see that ${\mathbb{R}}^n$ is homotopy equivalent to a point. It follows that$${\pi }_1({\mathbb{R}}^n)=0,\forall n\ge 0.$$

Example 2.23. As we will prove in Section 3 and Section 6,$${\pi }_1(S^1)=\mathbb{Z},\text{and}{\pi }_1(S^n)=0,\forall n>1.$$

Example 2.24. Let $T^n=(S^1{)}^n$ be the $n$-dim torus. Then$${\pi }_1(T^n)={\mathbb{Z}}^n.$$

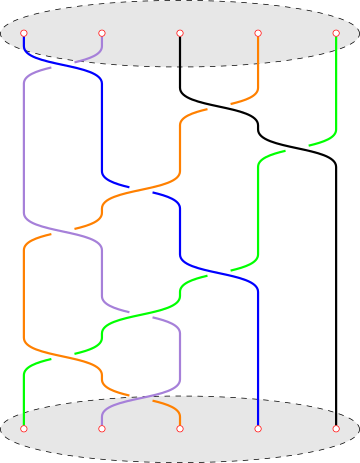
Example 2.25 (Braid groups). Artin’s braid group ${\mathrm{Br}}_n$ of $n$ strings can be realized as mapping class group (symmetry group) of a disk of $n$ punctures. It has the following finite presentation: $$\begin{array}{rcl}{\mathrm{Br}}_n=⟨b_1,\dots ,b_{n-1}\mid & b_i{b}_j{b}_i=b_j{b}_i{b}_j& \forall |j-i|=1,\\ & b_j{b}_i=b_i{b}_j& \forall |j-i|>1⟩.\end{array}$$Braid groups can be also realized as fundamental groups.

Let $X\in \mathsf{Top}$. The $n^{\mathrm{th}}$ (ordered) configuration space of $X$ is the set of $n$ pairwise distinct points in $X$: $${\mathrm{Conf}}_n(X):=\{\underline{x}=(x_1,\dots ,x_n)\in X^n\mid x_i\ne x_j,\forall i\ne j\}.$$There is a natural action of the permutation group $S_n$ on ${\mathrm{Conf}}_n(X)$ given by $$\begin{array}{rl}{S}_n\times {\mathrm{Conf}}_n(X)& ⟶{\mathrm{Conf}}_n(X)\\ (\sigma ,\underline{x})& ⟼\sigma (\underline{x})=(x_{\sigma (1)},x_{\sigma (2)},\dots ,x_{\sigma (n)}).\end{array}$$The unordered configuration space of $X$ is the orbit space of this action: $${\mathrm{UConf}}_n(X)={\mathrm{Conf}}_n(X)/S_n.$$

A classical result says $${\mathrm{Br}}_n\cong {\pi }_1({\mathrm{UConf}}_n({\mathbb{R}}^2))\cong {\pi }_1({\mathrm{UConf}}_n(D^2)).$$

Moreover, elements in this (fundamental) group can be visulized as braids in ${\mathbb{R}}^3$ as follows. Fix $n$ distinct points $Z_1,\cdots ,Z_n$ in ${\mathbb{R}}^2$. A geometric braid is an $n$-tuple $\Psi =({\psi }_1,\dots ,{\psi }_n)$ of paths $${\psi }_i:[0,1]\to {\mathbb{R}}^2\times I\subset {\mathbb{R}}^3$$such that

•	${\psi }_i(0)=Z_i\times \{0\}$;
•	${\psi }_i(1)=Z_{\sigma (i)}\times \{1\}$ for some permutation $\sigma$ of $\{1,\dots ,n\}$;
•	$\{{\psi }_1(t),\dots ,{\psi }_n(t)\}$ are distinct points in ${\mathbb{R}}^2\times \{t\}$, for any $0\le t\le 1$.

The product of geometric braids follows the same way as product of paths (in the fundamental group). The isotopy class of all braids on ${\mathbb{R}}^3$ with the product above form the braid group. See Figure 4 for a braid$$b_1{b}_3{b}_4{b}_2^{-1}{b}_1{b}_3{b}_2^{-1}{b}_1{b}_2^{-1}.$$

[ht]

Figure 4. Classical braids