2. 拓扑空间与连续映射 (II)
2.1积空间
在这一节中, 我们从两个拓扑空间 和 出发, 构造它们笛卡儿积 上的一个拓扑. 在定义结束之后我们就能够说 的标准拓扑就是 与自己的 “笛卡儿积” 上的积拓扑.
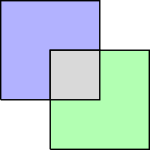
令 与 为拓扑空间. 设 是 的开集, 是 的开集. 如果我们希望在 上定义拓扑, 自然而然地我们希望 应该是这个拓扑的开集. 但是有一点微妙的地方应该注意, 子集族不能构成一个拓扑. 如果我们直观地将形如 的子集叫做 “开箱子 (openbox)”1 的话, 那么开箱子的并不一定是开箱子 (图 1).
图 1: 开箱子的并不是开箱子, 但交是
为了弥补这一点, 我们强行定义积拓扑的开集为一堆开箱子的并. 即: 为开, 如果存在一族 的开集 , 一族 的开集 , 使得 .
按照这个定义, 开集的并一定是开集. 我们来验证两个开集的交是开集: 设则仍然是开箱子的并.
我们约定, 今后若无特别申明, 若 , 为拓扑空间, 记号 总代表笛卡儿积上的积拓扑, 并称它为积空间.
积空间 上有两个自然的投影映射这两个映射都是连续的. 它们满足如下泛性质.
命题 2.1.1 (积空间的泛性质). 令 , , 为拓扑空间. 令 , 为连续映射. 则存在唯一连续映射 , 使得 与 成立.
证明. 定义 . 为了证明 连续, 只需证明 为开集, 其中 是 的开集, 是 的开集. 今有因 , 连续, 及 为开. 因此 , 为开.
2.1.2 (抽象的废话). 设 , 和 是三个拓扑空间. 按照上面的操作, 我们可以定义 以及 上面的积拓扑. 我们一定会默许地认为这两个空间是 “显然地” 同胚的. 我们也可以按照上面的构造, 定义三个空间的积空间 , 并且认为 以及 都 “显然地” 与 同胚. 在数学里, 我们常常会碰到这样 “平凡” 的问题. 而使用 “泛性质” 则能够让我们不必分析具体的构造而断言 “平凡” 的问题有确定的回答.
具体到上述问题, 我们来考虑一个大交换图在这个图里, , 与 都是由泛性质诱导的. 通过 “图上追踪”, 我们能够验证 , 对 都成立. 因此由 的泛性质的唯一性, 我们知道必有 . 类似可以验证 .
在这个论证过程中, “什么严肃的数学都没有发生”, 我们不需要进行思考. 因此这样的论证叫做 “抽象的废话”. 关于抽象废话的标准教材是 S. Mac Lane 的书 “数学工作者必知的范畴学”.
2.2基与子基
在积拓扑的构造中, 开箱子起到了决定性的作用. 使用一些具有特别特性的集合来构造开集在拓扑中十分常见. 我们因此从中抽出一个特别的概念: 拓扑基.
令 为集合. 令 为 的一个子集族. 我们称 是 上的一个拓扑基, 如果它满足如下属性:
对任何 , 存在 , 使得 . | |
若 , 则存在一族 中元素 , 使得 . |
比如, 在积拓扑的定义中, 开箱子的全体虽然不构成拓扑, 但构成了一个拓扑基.
如果 是一个集合, 是 上的一个拓扑基, 我们定义由 决定的拓扑如下: 的子集 叫做开集, 如果它是 中一族元素的并. 按照定义, 开集的并是开集; 拓扑基定义的第一条性质保证了 是开集; 取 , 我们知道空集是开集. 最后, 拓扑基定义的第二个条件保证了两个开集的交也是开集, 事实上, 如果 , , , 其中 , 则是开集.
如果 是一个拓扑空间, 是 的一个拓扑基. 如果 决定的拓扑就是 , 那么我们就说 生成了 .
例 2.2.1.
1. | 开箱子生成了两个空间的积拓扑. |
2. | 如果 是度量空间, 那么 的一切开球 生成了度量拓扑. 事实上, 选择 便足矣. |
3. | 若 是 一族子集. 令根据集合相交的约定, , 是 上的一个拓扑基. 我们称 是 的一个拓扑子基. 注意, 任何 的子集族都可以看作某个拓扑的子基. |
2.3始拓扑
令 是集合, 是一族拓扑空间, 是一族映射. 定义以 为子基生成的拓扑叫做集合 关于映射 的始拓扑.
命题 2.3.1. 记号如上. 赋予 始拓扑. 则对任何拓扑空间 , 任何映射 , 连续的必要且充分条件是对任何 , 是连续映射.
这是命题 2.2.2 的直接推论. 令 , , 我们可以说 的始拓扑是令 都连续的最粗的拓扑.
使用始拓扑可以很方便地定义任意多个空间的积拓扑. 设 是一族拓扑空间. 我们定义 的积拓扑为投影映射 的始拓扑. 于是命题 2.3.1 推出如下积拓扑的泛性质.
命题 2.3.2. 令 为一族拓扑空间. 赋予 积拓扑. 令 为一族连续映射. 则存在唯一连续映射 , 使得 . 这映射 通常用记号 来代表.
今后, 除非特别申明, 但凡使用记号 , 我们总是使用积拓扑.
注意, 如果我们展开始拓扑的定义, 那么积拓扑的一组基是一种特殊的开箱子:其中 是开集, 但是只有有限个 不等于 . 我们把这样的开箱子叫做 “好箱子”. 只选择好箱子做基而抛弃了其它箱子似乎不太自然. 但是命题 2.3.2 告诉我们实际上如果我们希望乘积映射 对任何 都连续的话, 我们只能使用好开箱子做基.
使用一切开箱子做基也决定了一个拓扑, 叫做 “箱拓扑”. 箱拓扑是一般拓扑学里常见的反例, 但是对于我们的课程并不重要.
2.4空间上的空间
令 为一个拓扑空间. 一个 上的空间 (space over ), 或 -空间 (-space), 是指偶对 , 其中 为拓扑空间, 为一个连续映射.
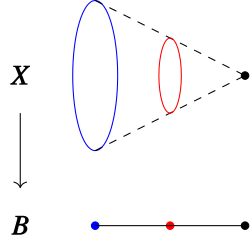
我们可以想象一个 -空间为一族空间 , 其中 (叫做点 的纤维 (fiber)), 并且 “随着 连续变化” (图 2).
图 2: 一族连续变化的椭圆
采取此观点时, 一般习惯性将 叫做底空间 (base space), 叫做全空间 (total space), 并且我们在黑板上一般用竖着的箭头来表示.
例 2.4.1 (平凡 -空间). 令 为任一拓扑空间. 则积空间 可以看作一个 -空间. 同胚于积空间的 -空间叫做平凡 -空间. 平凡 -空间的特点是所有的纤维都是 , 并且它们的 “相对位置” 没有产生变化.
例 2.4.2 (Möbius 带). 图 3 描述了著名的 Möbius 带 .
图 3: Möbius 带
即使我们没有明显地写出它在 中的方程 2, 读者应该能够想象出它的子空间拓扑结构. 图中的黑线是一个与 同胚的空间. 将 上一个点 “沿着竖线移动” 可以定义出一个从 到 的连续映射. 映射 的任何一个纤维都同胚于闭区间 , 但是我们今后会证明, 不同胚于 , 也就是说 不是一个平凡的 -空间.
例 2.4.3. 令 , 令以及令 . 则 是一个 -空间. 对于 , 是多项式的根的全体. 因此, 这个 -空间 “描述了” 当参数 “连续变化” 时, 的根如何随着 相应地变化.
如果 , 是两个 -空间. 一个从 到 的 连续 -映射是指一个连续映射 , 满足 . 因此, 连续 -映射恰好是那些保持纤维 (即把 映入 ) 的连续映射.
如果 是一族 -空间. 则我们定义 关于 的纤维积 (fiber product) 如下. 作为集合, 它是令 为 在子集 的限制. 我们赋予关于 的始拓扑.
注意. 记号过于繁琐, 在没有歧义时, 我们通常只使用记号两个 -空间 , 的纤维积通常用记号 , 或者更简略的 来表示.
如果我们把每个 看作 “一族由 参数化的连续变化的空间” , 那么纤维积则对应了 “逐个纤维取积空间” .
当 是一个点的时候, 纤维积就是通常的积空间.
如果 是一个 -空间, 那么 就诱导了连续 -映射 这个映射被形象地叫做对角线映射 (diagonal map).
设 是一个 -空间. 设 是另一个 -空间. 令 . 则我们有如下交换图:注意, 如果 , 则有 . 因此, 如果我们将 看作 -空间, 叫做 -空间 (通过 ) 的底变换 (base change).
2.5Hausdorff 空间
我们一直在讨论空间和映射的定义. 现在我们来介绍一个 “拓扑性质”. 我们称一个拓扑空间 是 Hausdorff 空间, 如果对任何 上的两个不同点 , 存在 的邻域 , 的邻域 , 使得 .
读者应该能够验证下面的断言.
命题 2.5.1.
1. | Hausdorff 空间的单点子空间都是闭集. |
2. | 与 Hausdorff 空间同胚的空间是 Hausdorff 的. |
3. | 度量空间是 Hausdorff 空间. |
4. | 离散空间是 Hausdorff 空间. |
5. | Hausdorff 空间的子空间也是 Hausdorff 空间. |
6. | Sierpiński 空间不是 Hausdorff 空间. |
命题 2.5.3. 令 为连续映射. 设 为 Hausdorff 空间. 则是 的闭子集.
本节所学概念与例子
- 积拓扑 product topology
- 拓扑基 basis for a topology
- 拓扑子基 subbasis
- 始拓扑 initial topology
- -空间 -space
- 纤维 fiber
- Möbius 带
- 纤维积 fiber product
- 底变换 base change
- 对角线映射 diagonal map
- Hausdorff 空间 Hausdorff space
2.6习题
2.6.1 (序列的极限). 令 为拓扑空间. 令 是 中的一列点. 我们称 收敛于 (或者 是 的一个极限), 记做 , 如果对任何 的邻域 , 存在 , 使得 .
1. | 举例说明在一般的拓扑空间中, 一个序列可以有多于一个极限. |
2. | 证明在 Hausdorff 空间中, 序列的极限有至多一个极限. |
2.6.2 (第一可数空间). 拓扑空间 叫做 第一可数 (first countable), 如果下述性质成立: 对任何 , 存在一族 的邻域 , 使得任何 的邻域 都包含某个 .
1. | 证明度量空间是第一可数的. |
2. | 设 为第一可数, 为拓扑空间之间映射. 证明 连续的必要充分条件是: 对任意 , 任意收敛于 的 上序列 , 都有 . |
2.6.3 (第二可数空间). 一个拓扑空间 叫做第二可数 (second countable) 的, 如果它有一个拓扑基 , 且 是个可数集合.
1. | 判断下列空间是否第二可数
| ||||||||||
2. | 证明下述 Lindelöf 定理: 若 第二可数, 是 的开覆盖, 则存在 的可数子集 , 使得 . |
2.6.4 (非分歧映射). 连续映射 叫做非分歧的 (unramified map), 如果对任意 , 都存在它的邻域 , 使得 是单射.
1. | 若 非分歧, 则对任意 , 是 的离散子空间. |
2. | 映射 有离散的纤维, 但它不是非分歧的. |
3. | 为非分歧的必要且充分条件是对角映射 是开嵌入. |
2.6.5 (局部同胚). 连续映射 叫做局部同胚 (local homeomorphism) (或 平展映射 (étale map)), 如果任何 都有邻域 , 使得 是 的开子空间, 且 是同胚.
1. | 局部同胚是开映射. |
2. | |
3. | 证明 是局部同胚的必要且充分条件是 是非分歧的开映射 (见 1.6.7, 2.6.4). 我们将在习题 5.8.3 提供一个不是局部同胚的非分歧满射的例子. |
2.6.6 (分离映射). 连续映射 叫做分离映射 (separated map), 如果对角线映射 是闭嵌入. 特别地, 如果 是单点集合, 那么 分离当且仅当 为 Hausdorff 空间.
1. | 证明下列断言等价.
| ||||||||
2. | 设 以及 是两个连续映射.
| ||||||||
3. | 若 是一族分离映射, 则典则映射 是分离映射. 特别地, Hausdorff 空间的积空间是 Hausdorff 空间. | ||||||||
4. | 若 是分离映射. 令 为连续映射, 则底变换 是否一定是分离映射? | ||||||||
5. | 若连续映射 的所有纤维都是 Hausdorff 空间, 是否一定分离? |
2.6.7 (Zariski 拓扑). 集合 的子集 叫做 Zariski 闭集, 如果存在 中多项式 , 使得 . 如果 的补集是 Zariski 闭集, 那么我们称 是 Zariski 开集.
1. | 的 Zariski 开集构成了一个拓扑, 称为 Zariski 拓扑. |
2. | 对于 , 我们可以把 看作 的线性子空间. 验证 的 Zariski 拓扑与它从 那里继承的 Zariski 子空间拓扑是一样的. |
3. | “俨开集 (distinguished open)” , 其中 , 构成了 上 Zariski 拓扑的一个拓扑基. |
4. | 令 为 中多项式. 证明映射关于定义域和靶空间 Zariski 拓扑连续. |
5. | 上的 Zariski 拓扑是否 的 Zariski 拓扑的积拓扑? |
2.6.8 (H. Furstenberg 关于素数无限性的拓扑证明 3). 对整数 , 定义 . 以 为子基决定的集合 上的一个拓扑 .
1. | 证明每个 关于拓扑 既开又闭. |
2. | 证明有限子集在拓扑 下非开. |
3. | 证明 . 由此推出有无限个素数. |
2.6.9 (Hilbert 空间 ). 令 为一切满足的映射 构成的集合.
1. | 定义验证 是 的度量. |
2. | 证明 与 是连续映射. [因此 是一个拓扑向量空间 (topological vector space).] |
3. | 证明 是第二可数 Hausdorff 空间. |
4. | 证明 Hilbert 方块 在 中内部为空. |
5. | 证明 同胚于积空间 . |
脚注
1. | “开” 在这里是形容词, 不是动词. |
2. | 图 3 所画的 是从 到 的映射的像. 黑色的 是 子空间 的像. |
3. | On the infinitude of primes. American Mathematical Monthly. 62 (5): 353. 1955. |