作业: 曲线曲面积分的计算

课堂补充

A1)	给定 $\sigma$-有限的测度空间 $(X,\mathcal{A},\mu )$, 正可测函数 $\rho$ 几乎处处有界, 我们课上证明了 $\nu =\rho \mu$ 是 $(X,\mathcal{A})$ 上 $\sigma$-有限的测度. $f$ 是 $(X,\mathcal{A},\mu )$ 上的可测函数. 证明, $f\rho \in L^1(X,\mathcal{A},\mu )$ 当且仅当 $f\in L^1(X,\mathcal{A},\nu )$ ($L^1$ 表示它可积分) . 进一步, 在此情形下, 我们有$${\int }_{X}f(x)d\nu (x)={\int }_{X}f(x)\rho (x)d\mu (x).$$(提示: 证明遵循标准操作的步骤: 1) 对 $f(x)=1_A$ 验证, 其中 $A\in \mathcal{A}$) . 2) 对阶梯函数验证. 3) 通过取上升的简单函数逼近正函数 $f$ 对正函数验证. 4) 对于一般的函数, 将函数的实部和虚部拆成正负部分并利用线性完成证明. )
A2)	我们在 ${\mathbb{R}}^2$ 上给 Lebesgue 测度 $m_2$. 考虑投影映射$${\pi }_1:{\mathbb{R}}^2\to \mathbb{R},(x,y)\mapsto x.$$证明, ${\mathbb{R}}^1$ 上的 Lebesgue 测度 ${\pi }_{1\ast }{m}_2$ 不是 $\sigma$-有限的,
A3)	假设 $n⩾2$, $f\in C^{\infty }({\mathbb{R}}^{n-1})$, 我们用如下的方式来参数化其图像 ${\Gamma }_f$: $$\Phi :{\mathbb{R}}^{n-1}\to {\mathbb{R}}^n,x\mapsto (x,f(x)).$$证明, $$\det \left({}^t\mathrm{Jac}(\Phi )\cdot \mathrm{Jac}(\Phi )\right)=1+|\nabla f{|}^2.$$
A4)	(换元积分公式, 条件更弱) 如果 $\Phi :{\Omega }_1\to {\Omega }_2$ 是同胚 (即该映射及其逆都是连续的) 并且 $\Phi$ 是连续可微的, 对任意的可积函数 $f(y)\in L^1({\Omega }_2,dy)$, 我们有$${\int }_{{\Omega }_2}f(y)dy={\int }_{{\Omega }_1}(f\circ \Phi )(x)|J_{\Phi }(x)|dx.$$
A5)	假设 $M\subset {\mathbb{R}}^n$ 是 $n-1$-维的子流形, 考虑投影映射$$\pi :M\to {\mathbb{R}}^{n-1},(x_1,\cdots ,x_{n-1},x_n)\mapsto (x_1,\cdots ,x_{n-1}).$$令$$\mathrm{Sing}(\pi )=\{x\in M|\mathrm{rank}d\pi (x)<n-1\}.$$证明, $\pi (\mathrm{Sing}(\pi ))\subset {\mathbb{R}}^{n-1}$ 是零测集 (用 ${\mathbb{R}}^{n-1}$ 上的 Lebesgue 测度来看) . 对于 $x^{\prime }=(x_1,\cdots ,x_{n-1})\in {\mathbb{R}}^{n-1}$, 我们定义直线$$L_{x^{\prime }}=\{(x_1,\cdots ,x_{n-1},t)|t\in \mathbb{R}\}={\pi }^{-1}(x^{\prime })\subset {\mathbb{R}}^n.$$证明, $$\pi (\mathrm{Sing}(\pi ))=\{x^{\prime }\in {\mathbb{R}}^{n-1}|\text{直线}{L}_{x^{\prime }}\text{与}M\text{相切}\}.$$其中, $L_{x^{\prime }}$ 与 $M$ 相切指的是存在 $p\in M$, 使得 $p\in L_{x^{\prime }}$ 并且 $T_p{L}_{x^{\prime }}\subset T_{p}M$.
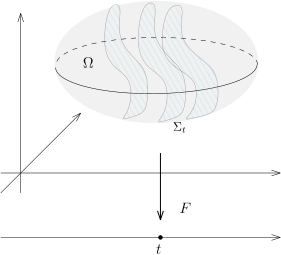
A6)	(一个 “扭曲” 的 Fubini) $\Omega \subset {\mathbb{R}}^n$ 是开集, $F:U\to \mathbb{R}$ 是光滑映射. 假设对任意的 $x\in U$, $dF(x)\ne 0$ (从而, ${\Sigma }_t=F^{-1}(t)$ 是余 $1$ 维子流形) . 那么, 对任意的 $U$ 上的可积函数 $f$, 我们有$${\int }_{\Omega }f(x)dx={\int }_{\mathbb{R}}\left({\int }_{{\Sigma }_t}\frac{f}{|\nabla F|}d{\sigma }_t\right)dt,$$其中, $d{\sigma }_t$ 是 ${\Sigma }_t$ 上的子流形测度.

积分的计算 (换元积分公式)

我们有比较常用的坐标变换 (主要是前两种) :

1.	极坐标 $(r,\phi )\mapsto (x,y)=(r\cos \phi ,r\sin \phi )$;
2.	球坐标 $(r,\theta ,\phi )\mapsto (x,y,z)=(r\sin \theta \cos \phi ,r\sin \theta \sin \phi ,r\cos \theta )$;
3.	双曲坐标 (Rindler 坐标) $(t,x)\mapsto (T,X)=(x\sinh t,x\cosh t)$, 其中 $\sinh t=\frac{e^t-e^{-t}}{2},\cosh t=\frac{e^t+e^{-t}}{2}$;
4.	抛物坐标 $(u,v)\mapsto (x,y)=(u^2-v^2,2uv)$;
5.	椭圆坐标 $(u,v)\mapsto (x,y)=(c\cosh u\cos v,c\sinh u,\sin v)$, $c>0$ 是常数.

B1)	计算体积或者面积 (如果需要对参数分类讨论, 那么请至少处理一种情形) 1. 双纽线 $(x^2+y^2{)}^2=2a^2(x^2-y^2)$ 围成的面积. 2. 曲线 $(x^3+y^3{)}^2=x^2+y^2$ 的内部区域面积. 3. 曲线 $\frac{x^3}{a^3}+\frac{y^3}{b^3}=\frac{x^2}{h^2}+\frac{y^2}{k^2}$ 与坐标轴 $x=0,y=0$ 围成的面积. 4. 曲线 $(2x+y{)}^4=x^2-2y^2$ 围成的面积. 5. 曲线 $(\frac{x}{a}+\frac{y}{b}{)}^5=\frac{x^2{y}^2}{c^4}$ ($x>0,y>0$) 围成的面积. 6. 曲面 $(x^2+y^2+z^2{)}^3=\frac{a^6{z}^2}{x^2+y^2}$ 所围立体图形的体积. 7. 曲面 $(\frac{x^2}{a^2}+\frac{y^2}{b^2}{)}^2+\frac{z^4}{c^4}=1$ 内部的体积. 8. 曲面 $(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}{)}^4=\frac{xyz}{abc}$ ($x,y,z>0$) 所围立体图形的体积. 9. $(\frac{x}{a}+\frac{y}{b}{)}^2+(\frac{z}{c}{)}^2=1$ 所围立体图形的体积. 10. 曲面 $z=x^2+y^2,z=2(x^2+y^2),xy=a^2,xy=2a^2,x=2y,2x=y$ ($x>0,y>0$) 所围立体图形的体积.
B2)	设物体的质量由密度函数 $\rho$ 给出, 那么在区域 $V$ 内的总质量为 ${\int }_V\rho (x)dx$, $V$ 的质心坐标 $({\bar{x}}_1,\cdots ,{\bar{x}}_n)$ 由下式确定: $$\begin{array}{r}{\bar{x}}_i=\frac{{\int }_V{x}_i\rho (x)dx}{{\int }_V\rho (x)dx}.\end{array}$$ 1. 计算球 $x^2+y^2+z^2⩽2az$ 的质量及质心坐标, 其中密度函数 $\rho (x,y,z)=\frac{k}{\sqrt{x^2+y^2+z^2}}$, $k>0$ 是常数. 2. 求由抛物面 $x^2+y^2=2az$ 及球面 $x^2+y^2+z^2=3a^2$ 围成的均质 ($\rho \equiv 1$) 物体的质心坐标.
B3)	假设 $\rho$ 是 ${\mathbb{R}}^3$ 上非负可积的函数 (如果一个物体的质量函数是 $\rho$ 的话) , 它所对应的引力势能 $\Phi (x)$ 和引力场 $G(x)$ 由下式给出: $$\begin{array}{r}\Phi (x)=-{\int }_{{\mathbb{R}}^3}\frac{\rho (y)}{|x-y|}dy,G(x)=-\nabla \Phi (x)\end{array}$$我们假设区域 $V\subset {\mathbb{R}}^3$ 是开区域, ${\rho }_0>0$ 是常数, $$\begin{array}{r}\rho (x)=\{\begin{array}{ll}{\rho }_0,& x\in V\\ 0,& x\in {\mathbb{R}}^3\setminus V\end{array}\end{array}$$试计算如下情形下的 $\Phi (x)$ 和 $G(x)$: 1. $V=\{x\in {\mathbb{R}}^3:|x{|}^2<R^2\}$ 是球体. 2. $V=\{x=(x_1,x_2,x_3)\in {\mathbb{R}}^3:x_1^2+x_2^2<R^2,0<x_3<h\}$ 是圆柱体. * 3. $V=\{x=(x_1,x_2,x_3)\in {\mathbb{R}}^3:x_3^2>\frac{h^2}{R^2}(x_1^2+x_2^2),0<x_3<h\}$ 是圆锥体. * (* 请注意, 后两问极其困难, 请勿直接尝试)
B4)	(Newton 壳层 (shell) 定理: 关于球对称密度分布的引力) 假设$$\begin{array}{r}\rho (x)=\{\begin{array}{ll}f(|x|),& r<|x|<R;\\ 0,& |x|>R\text{ 或 }|x|<r.\end{array}\end{array}$$其中 $f$ 是在 $[r,R])$ 上定义的非负可积函数. 证明: 1. 对球外一点 ($|x|>R$) 产生的引力与球的所有质量集中于球心的质点产生的引力一样. 2. 球壳对球壳内任何一点 ($|x|<r$) 产生的引力 (合力) 为零.

曲面／曲线／子流形上的积分计算

C1)

计算下列的曲线积分: 1. 计算 ${\mathbb{R}}^3$ 中曲线 $C$ 的长度, 其中参数曲线 $C$ 由 $t\mapsto (a\cos (t),b\sin (t),bt)$ 给出, 其中 $t\in [0,2\pi ]$; 计算 ${\int }_C\frac{z^2}{x^{+}{y}^2}ds$, 其中 $ds$ 为 $C$ 上的子流形测度. 2. 假设 $C$ 是 ${\mathbb{R}}^3$ 中 $x^2+y^2+z^2=a^2$ 与 $x+y+z=0$ 所截出的曲线, 试计算 ${\int }_{C}xyds$. 3. $C$ 是参数曲线 $(a(t-\sin t),a(1-\cos t))$, 其中 $t\in [0,2\pi ]$. 计算积分 ${\int }_C{y}^{2}ds$. 4. 平面上的曲线 $C$ 在极坐标系下的方程为 $r=f(\theta )$, 其中 $f$ 是连续可微的, $\alpha \theta \beta$. 证明, $C$ 的长度为$${\int }_{\alpha }^{\beta }\sqrt{|f(\theta ){|}^2+|f^{\prime }(\theta ){|}^2}d\theta .$$

C2)

计算下列的曲面积分: 1. 试计算 $x^2+y^2+z^2=a^2$ 与 $x^2+y^2=ax$ 相交得到的曲线在球面上围出的面积. 2. 试计算参数曲面 $\Sigma$ 的面积, 其中 $\Sigma$ 如下定义: $$[0,2\pi ]\times [0,2\pi ]\to {\mathbb{R}}^3,(\vartheta ,\phi )\mapsto ((b+a\cos \vartheta )\cos \phi ,(b+a\sin \vartheta )\sin \phi ,a\sin \vartheta ),$$其中, 我们要求 $0<a<b$. 3. $C$ 是参数曲线 $(a(t-\sin t),a(1-\cos t))$, 其中 $t\in [0,2\pi ]$. 将 $C$ 在 ${\mathbb{R}}^3$ 中绕着 $x$ 轴旋转一周得到的曲面是 $\Sigma$, 试计算 $\Sigma$ 的面积. 4. $C$ 是平面上的抛物线段 $x=y^2$, 其中 $x\in [0,a]$. 将 $C$ 在 ${\mathbb{R}}^3$ 中绕着 $x$ 轴旋转一周得到的曲面是 $\Sigma$, 试计算 $\Sigma$ 的面积. 5. $\Sigma$ 是锥面 $z^2=x^2+y^2$ 被柱面 $x^2+y^2=2ax$ 所截下的部分, 计算曲面积分 ${\int }_{\Sigma }{x}^2{y}^2+y^2{z}^2+z^2{x}^{2}d\sigma$. 6. $\Sigma$ 是 ${\mathbb{R}}^3$ 中的柱面 $x^2+y^2=a^2$, 其中 $z\in [0,h]$, 计算曲面积分 ${\int }_{\Sigma }{x}^4+y^{4}d\sigma$. 7. $\Sigma$ 是 ${\mathbb{R}}^3$ 中的半球面 $x^2+y^2+z^2=1$, 其中 $z⩾0$, 计算曲面积分 ${\int }_{\Sigma }x+y+zd\sigma$. 8. $\Sigma$ 是 ${\mathbb{R}}^3$ 中的球面 $x^2+y^2+z^2=1$, 计算曲面积分 ${\int }_{\Sigma }{x}^{2}d\sigma$. 9. $\Sigma$ 是 ${\mathbb{R}}^3$ 中的球面上小帽子 $x^2+y^2+z^2=1$, $z⩾h>0$, 计算曲面积分 ${\int }_{\Sigma }\frac{1}{z}d\sigma$. 10. $\Sigma$ 是 ${\mathbb{R}}^3$ 中的参数曲面: $(u,v)\mapsto (u\cos v,u\sin v,v)$, 其中 $(u,v)\in [0,a]\times [0,2\pi ]$. 计算曲面积分 ${\int }_{\Sigma }zd\sigma$. 11. $\Sigma$ 是 ${\mathbb{R}}^3$ 中的球面 $x^2+y^2+z^2=1$, $f$ 是 $\mathbb{R}$ 上的连续函数. 证明, $${\int }_{\Sigma }f(ax+by+cz)d\sigma =2\pi {\int }_{-1}^{1}f((a^2+b^2+c^2{)}^{\frac{1}{2}}t)dt.$$

寄语. In my free time I do differential and integral calculus.

— Karl Marx