抽象积分理论的一些具体例子与讨论 给定测度空间 ( X , A , μ ) f : X → [ 0 , + ∞ ] ∫ X fd μ : = 0 ⩽ φ ⩽ f φ ∈ E ( X ) sup ∫ X φ d μ . f : X → C ∫ X ∣ f ∣ d μ < ∞ f
我们先看一个例子:
假设 X = Z ⩾ 1 = { 1 , 2 , ⋯ , n , ⋯ } A = P ( X ) X σ μ : Z ⩾ 1 → [ 0 , ∞ ] , A ↦ μ ( A ) = ∣ A ∣. ( Z ⩾ 1 , P ( Z ⩾ 1 , μ ) ) f : Z ⩾ 1 → C , n ↦ f ( n ) , A = P ( X ) f n = 1 ∑ ∞ ∣ f ( n ) ∣ < ∞ ∫ Z ⩾ 1 fd μ = n = 1 ∑ ∞ f ( n ) .
类似于上学期我们所学的关于级数收敛或者反常积分的判别法, 我们对于积分的收敛性 (即一个函数是否可积分) 有如下的判别准则:
f h ( X , A , μ ) h ∣ f ( x ) ∣ ⩽ h ( x ) f
证明. 令
B = { x ∈ X ∣ ∣ f ( x ) > g ( x ) } , 按照命题中的要求,
μ ( B ) = 0 . 我们令
f 1 ( x ) = f ( x ) 1 B c ( x ) , 那么, 对所有的
x ∈ X , 我们都有
∣ f 1 ( x ) ∣ ⩽ h ( x ) . 作为正函数, 我们自然有
∫ X ∣ f 1 ∣ d μ ⩽ ∫ X ∣ h ∣ d μ < ∞. 所以
f 1 ( x ) 是可积的. 为了说明
f ( x ) 是可积分的, 我们比较
∣ f ( x ) ∣ 与
∣ f 1 ( x ) ∣ : 对于任意的
x , 都有
∣ f 1 ( x ) ∣ ⩽ ∣ f ( x ) ∣ , 所以
∫ X ∣ f 1 ∣ d μ ⩽ ∫ X ∣ f ∣ d μ . 这两个函数只在零测集
B 上有差别. 按照积分的定义, 我们有
∫ X ∣ f ∣ d μ : = 0 ⩽ φ ⩽ ∣ f ∣ φ ∈ E ( X ) sup ∫ X φ d μ . 对于简单函数而言, 我们在一个零测集上改变函数值 (全改为零) 是不影响它的积分的, 这可以用简单函数的积分定义直接看出, 所以, 我们总是可以假设上面积分定义中的函数
φ 在
B 上取零. 此时,
φ ∈ E ( X ) 并且
0 ⩽ φ ⩽ ∣ f ∣ 意味着
φ ∈ E ( X ) 并且
0 ⩽ φ ⩽ ∣ f 1 ∣ , 这说明
∫ X ∣ f 1 ∣ d μ = ∫ X ∣ f ∣ d μ . 这就给出了命题的证明.
尽管我们现在还没有足够好的工作计算积分 (目前只会计算简单函数的积分! ) , 但是通过这个比较的判别法, 我们可以判断函数的可积性. 下面的几个例子很有启发性:
1)
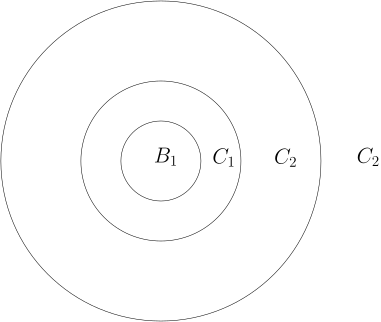
给定 R n f x ∈ R n f ∣ f ( x ) ∣ ⩽ 1 + ∣ x ∣ n + ε C , ε > 0 f
根据上面的判断法则, 我们只要证明函数 f ( x ) = 1 + ∣ x ∣ n + ε C R n B R = { x ∈ R n ∣ ∣ ∣ x ∣ ⩽ R } C k = B 2 k + 1 − B 2 k R n = B 1 ∪ C 1 ∪ C 2 ∪ ⋯ ∪ C k ∪ ⋯
尽管我们现在还不能计算这些环面或者球面的体积, 但是, 由于 B 1 C 1 4 a m ( C 1 ) + m ( B ) ⩽ a C k C 1 R n → R n , x ↦ 2 k x , m ( C k ) = ( 2 k ) n m ( C 1 ) ⩽ 2 kn a . C k f ( x ) = 1 + ∣ x ∣ n + ε C ⩽ 1 + ∣ 2 k ∣ n + ε C ⩽ ∣ 2 k ∣ n + ε C . h ( x ) = C 1 B 1 + k = 1 ∑ ∞ ∣ 2 k ∣ n + ε C 1 C k . f ( x ) ⩽ h ( x ) h ∫ R n h d m = C m ( B 1 ) + k = 1 ∑ ∞ ∣ 2 k ∣ n + ε C m ( C k ) ⩽ C m ( B 1 ) + k = 1 ∑ ∞ ∣ 2 k ∣ n + ε C 2 kn a = C m ( B 1 ) + C a k = 1 ∑ ∞ 2 k ε 1 .
2)
我们考虑 R f ( x ) = x sin ( x ) f f ∣ ∣ x sin ( x ) ∣ ∣
下面的命题很有用, 它的证明也很值得学习:
f ( X , A , μ )
证明. 我们上次课证明了 1)
⇒ 2). 反之, 假设
∫ X fd μ = 0 . 对每个自然数
n , 我们考虑集合
A n = { x ∈ X ∣ ∣ f ( x ) ⩾ n 1 } . 根据定义, 我们自然有
f ( x ) ⩾ n 1 1 A n ( x ) . 所以, 我们有如下积分不等式:
0 = ∫ X fd μ ⩾ ∫ X n 1 1 A n d μ = n 1 μ ( A n ) . 从而对所有
n ⩾ 1 ,
μ ( A n ) = 0 . 然而, 由于
f 是正函数, 我们显然有
{ x ∣ f ( x ) = 0 } = { x ∣ f ( x ) > 0 } = n ⩾ 1 ⋃ A n . 所以,
μ ({ x ∣ f ( x ) = 0 }) = 0 , 即
f 几乎处处为零.
在 R 1 m f : R 1 → C Lebesgue 可积的 . 我们可以探讨我们刚刚建立的抽象积分理论与上学期 Riemann 积分的联系. 为了简单期间, 我们在下面的定理中假设 f
假定 f [ a , b ] f 是 Lebesgue 可测的并且其 Lebesgue 积分恰为其 Riemann 积分.
证明.
我们利用 Darboux 上下和来逼近函数的积分. 为此, 任取 [ a , b ] I = [ x 0 , x 1 ] ∪ [ x 1 , x 2 ] ∪ ⋯ ∪ [ x n − 1 , x n ] x 0 = a x n = b x 0 < x 1 < ⋯ < x n M k = x ∈ [ x k − 1 , x k ] sup f ( x ) , m k = x ∈ [ x k − 1 , x k ] inf f ( x ) . F I ( x ) = k = 1 ∑ n M k 1 [ x k − 1 , x k ] , F I ( x ) = k = 1 ∑ n m k 1 [ x k − 1 , x k ] . ∫ [ a , b ] F I d m , ∫ [ a , b ] F I d m I
我们现在选取特殊分划: 对任意的
n , 分划
I n 对应为区间
[ a , b ] 的
2 n 等分. 此时, 我们将对应的简单函数
F I n ( x ) 和
F I n ( x ) 简记为
F n 和
F n . 很明显, 我们就得到两个单调的序列
{ F n } n ⩾ 1 和
{ F n } n ⩾ 1 . 由于有界单调数列一定有极限, 所以, 存在可测函数
F 和
F , 使得
F n ↘ F , F n ↗ F . 由于
F n ⩾ F n , 所以
F ⩾ F . 按照 Riemann 积分的定义, 上和的极限等于下和的极限 (都等于该函数的积分) , 即
n → ∞ lim ∫ [ a , b ] F n d m = n → ∞ lim ∫ [ a , b ] F n d m . 根据 Beppo Levi 定理, 我们就有
∫ [ a , b ] F d m = ∫ [ a , b ] F d m = Riemann 积分 ∫ a b f ( x ) d x . 所以, (利用积分的线性, 即将证明)
∫ [ a , b ] F − F = 0. 从而, 由于
F = F ⩾ 0 , 所以, 在一个零测集之外, 我们有
F = F , 几乎处处 . 另外, 按照定义, 我们还有
F ⩾ f ⩾ F 这说明, 在差一个零测度的子集意义下 (要用到测度的完备性, 我们不去追究这个细节) , 我们有
F = f = F . 所以, 上述的论证说明了
f 是可测的并且它的 Riemann 积分与 Lebesgue 积分是一致的.
如果 f [ a , b ]
Beppo Levi 定理的应用: Fatou 引理与 Lebesgue 控制收敛定理 我们上周课程最后讲到了 Beppo Levi 定理以及一个技术性的逼近定理 (存在上升的简单函数列逼近正可测函数) . 利用这个两个结论, 我们有很多有趣有意义的推论:
f g ( X , A , μ ) a , b ∈ R ⩾ 0 ∫ X a f + b g d μ = a ∫ X fd μ + b ∫ X g d μ .
证明. 我们选取单调上升的简单函数序列
{ f i } i ⩾ 1 和
{ g i } i ⩾ 1 , 使得它们分别逐点收敛到
f 和
g . 所以,
{ a f i + b g i } i ⩾ 1 也是单调上升的简单函数序列并且逐点收敛到
a f + b g . 根据积分的对于简单函数的线性, 对每个
i , 我们有
∫ X a f i + b g i d μ = a ∫ X f i d μ + b ∫ X g i d μ . 令
i → ∞ , 由 Beppo Levi 定理, 左右两端分别收敛到推论中要证明等式的左右两端.
Beppo Levi 定理的一个重要推论是 Fatou 引理:
{ f i } i ⩾ 1 ( X , A , μ ) ∫ X i → ∞ lim inf f i d μ ⩽ i → ∞ lim inf ∫ X f i d μ , x ∈ X ( i → ∞ lim inf f i ) ( x ) = i → ∞ lim inf f i ( x ) { f i } i ⩾ 1 f x i → ∞ lim f i ( x ) = f ( x ) ∫ X fd μ ⩽ i → ∞ lim inf ∫ X f i d μ .
Fatou 引理叙述中的不等式一般而言不能取到等号, 同学们可以 (作业) 构造函数列 { f i } i ⩾ 1 f ∫ X fd μ < i → ∞ lim inf ∫ X f i d μ .
证明之前, 有必要回忆 “下极限” 的概念: 给定实数序列
{ a i } i ⩾ 1 , 序列
{ i ⩾ p inf a i } p ⩾ 1 是递增的. 我们定义
i → ∞ lim inf a i = p → ∞ lim ( i ⩾ p inf a i ) . 证明. 令
f ( x ) = p → ∞ lim inf f p ( x ) . 我们定义函数列
{ g p ( x ) } p ⩾ 1 , 其中
g p ( x ) = i ⩾ p inf f i ( x ) . 那么,
{ g p ( x ) } p ⩾ 1 为上升的正函数序列并且逐点地收敛到
f ( x ) . 根据 Beppo Levi 定理, 我们有
p → ∞ lim ∫ X g p d μ = ∫ X fd μ . 然而, 根据
g p ( x ) 的定义, 对每个
x ∈ X , 我们有
g p ( x ) ⩽ f p ( x ) . 从而,
∫ X g p d μ ⩽ ∫ X f p d μ . 这表明
p → ∞ lim ∫ X g p d μ = p → ∞ lim inf ∫ X g p d μ ⩽ p → ∞ lim inf ∫ X f p d μ . 上面不等式左边就是
∫ X fd μ , 这就完成了 Fatou 引理第一部分的证明. 第二部分是第一部分的直接推论.
给定测度空间 ( X , A , μ ) L 1 ( X , A , μ ) ± ∞ − 1 × ± ∞
这是线性子空间: 对于任意的 f , g ∈ L 1 ( X , A , μ ) α , β ∈ C ∣ f ∣ ∣ g ∣ ∣ α ∣∣ f ∣ + ∣ β ∣∣ g ∣ x ∈ X ∣ α f ( x ) ∣ + ∣ β g ( x ) ∣ ⩽ ∣ α ∣∣ f ( x ) ∣ + ∣ β ∣∣ g ( x ) ∣ , α f + β g ∈ L 1 ( X , A , μ )
考虑几乎处处为零的函数空间N = { f ∈ L 1 ( X , A , μ ) ∣ ∣ f 几乎处处为零 } . N L 1 ( X , A , μ ) f , g ∈ N A B f ∣ ∣ A c ≡ 0 g ∣ ∣ B c ≡ 0 α , β ∈ C α f + β g ∣ ∣ ( A ∪ B ) c ≡ 0. A ∪ B α f + β g ∈ N
我们定义 L 1 ( X , A , μ ) L 1 ( X , A , μ ) = L 1 ( X , A , μ ) / N . L 1 ( X , A , μ )
对于 f ∈ L 1 ( X , A , μ ) [ f ] ⊂ L 1 ( X , A , μ ) f ∈ [ f ] L 1 ( X , A , μ ) [ f ] = 0 f ∈ N [ f ] = N f ∣ f ∣ f ∈ L 1 ( X , A , μ ) f = 0 ∫ X ∣ f ∣ d μ = 0
我们现在终于可以证明积分算子的线性了:
L 1 ( X , A , μ ) C ∫ X − d μ : L 1 ( X , A , μ ) → C , f ↦ ∫ X fd μ , C f ∈ L 1 ( X , A , μ ) ∣ ∫ X fd μ ∣ ⩽ ∫ X ∣ f ∣ d μ .
证明. 我们已经证明了 L 1 ( X , A , μ ) C f , g ∈ L 1 ( X , A , μ )
1)
如果 f g a , b ⩾ 0 ∫ X a f + b g d μ = a ∫ X fd μ + b ∫ X g d μ .
2)
f g a = 1 b = − 1 ∫ X f − g d μ = ∫ X fd μ − ∫ X g d μ . h = f − g h h = h + − h − h + + g = h − + f . ∫ X h + d μ + ∫ X g d μ = ∫ X h − d μ + ∫ X fd μ . ∫ X h d μ ∫ X h d μ = ∫ X h + d μ − ∫ X h − d μ , ∫ X f − g d μ = ∫ X h d μ = ∫ X h + d μ − ∫ X h − d μ = ∫ X fd μ − ∫ X g d μ .
3)
f g a , b ∈ R ⩾ 0 ∫ X a f + b g d μ = ∫ X ( a f + + b g + ) − ( a f − + b g − ) d μ = ∫ X ( a f + + b g + ) d μ − ∫ X ( a f − + b g − ) d μ = a ∫ X f + d μ + b ∫ X g + d μ − a ∫ X f − d μ − b ∫ X g − d μ .
4)
f g a , b ∈ R ∫ X fd μ = ∫ X f + d μ − ∫ X f − d μ = − ( ∫ X f − d μ − ∫ X f + d μ ) = − ∫ X fd μ . a b
5)
f g a , b ∈ C f g a b
至此, 我们完整地证明了积分的线性. 为了证明定理中的不等式, 选取复数
e i θ 0 , 使得
e i θ 0 ∫ X fd μ = ∣ ∣ ∫ X fd μ ∣ ∣ . 根据积分的线性, 我们有
∣ ∣ ∫ X fd μ ∣ ∣ = ∫ X e i θ 0 fd μ . 所以, 函数
e i θ 0 f 的虚数部分对积分没有贡献, 从而
∫ X e i θ 0 fd μ = ∫ X Re ( e i θ 0 f ) d μ ⩽ ∫ X Re ( e i θ 0 f ) + d μ ⩽ ∫ X ∣ f ∣ d μ . 最后一步, 我们用到了
Re ( e i θ 0 f ) + ⩽ ∣ f ∣ , 这是显然的.
一旦有了积分的线性, 我们就可以方便地证明很多命题了
(积分的区域可加性) 给定测度空间 ( X , A , μ ) f X f 支集 supp f supp f = { x ∈ X ∣ ∣ f ( x ) = 0 } . supp f ⊂ A ∈ A ∫ X fd μ ∫ A fd μ A , B ∈ A A ∩ B = ∅ f ⋅ 1 A f ⋅ 1 B ∫ A ∪ B f = ∫ A fd μ + ∫ B fd μ .
证明. 由于
∣ f ⋅ 1 A ∣ ⩽ ∣ f ∣ , 所以
f ⋅ 1 A 可积. 推论中的等式就是对
f ⋅ 1 A + f ⋅ 1 B 的积分应用线性.
在零测集上改变函数的值不会影响其积分, 也就是说, 如果 f 1 , f 2 ∈ L 1 ( X , A , μ ) f 1 = f 2 几乎处处, 那么∫ X f 1 d μ = ∫ X f 2 d μ .
证明. 按照要求,
f = f 1 − f 2 几乎处处是
0 , 所以其积分为
0 , 从而
0 = ∫ X fd μ = ∫ X f 1 − f 2 d μ = ∫ X f 1 d μ − ∫ X f 2 d μ . 映射∥ ⋅ ∥ L 1 ( X , A , μ ) : L 1 ( X , A , μ ) → R ⩾ 0 , [ f ] ↦ ∫ X ∣ f ∣ d μ , L 1 范数 , 对于 f ∈ L 1 ( X , A , μ ) ∥ f ∥ L 1 ( L 1 ( X , A , μ ) , ∥ ⋅ ∥ L 1 )
证明. 首先, 对于等价类
[ f ] 中的任何两个代表元
f 1 , f 2 ∈ [ f ] , 它们几乎处处相等, 所以
∣ f 1 ∣ = ∣ f 2 ∣ 几乎处处, 从而,
∥ [ f ] ∥ L 1 = ∫ X ∣ f 1 ∣ d μ = ∫ X ∣ f 2 ∣ d μ . 这表明映射是良好定义的. 另外, 我们知道
∣ ∣ ∫ X ∣ f ∣ d μ ∣ ∣ = 0 等价于在
L 1 ( X , A , μ ) 中
f = 0 . 所以,
∥ f ∥ L 1 = 0 等价于在
L 1 ( X , A , μ ) 中
f = 0 . 对于任意的
a , b ∈ C 和
a , b ∈ L 1 ( X , A , μ ) , 根据积分的线性, 我们有
∥ a f + b g ∥ L 1 = ∫ X ∣ ∣ a f + b g ∣ ∣ d μ ⩽ ∫ X ∣ a ∣∣ f ∣ + ∣ b ∣∣ g ∣ d μ = ∣ a ∣∥ f ∥ L 1 + ∣ b ∣∥ g ∥ L 1 . 这就说明了
∥ ⋅ ∥ L 1 是范数.
我们将证明 ( L 1 ( X , A , μ ) , ∥ ⋅ ∥ L 1 )
(子空间上的积分) 假定 Y ∈ A A ∣ ∣ Y = { A ∈ A ∣ A ⊂ Y } σ ι : Y → X , y ↦ y , A ∣ ∣ Y = ι ∗ A μ 限制到 A ∣ Y 上得到一个测度 μ ∣ ∣ Y A ∩ Y ⊂ A ∣ Y μ ∣ ∣ Y ( A ∩ Y ) = μ ( A ∩ Y ) ( Y , A ∣ ∣ Y , μ ∣ ∣ Y ) Y Y X X X
我们还必须做出如下的澄清 : 当 X = R n Y 1 μ ∣ ∣ Y 0
我们现在可以证明积分理论中最重要的收敛定理了, 它的应用渗透到近代分析的每个角落:
假定测度空间 ( X , A , μ ) { f i } i ⩾ 1 f N ∈ A x ∈ N c i → ∞ lim f i ( x ) = f ( x ) h ∈ L 1 ( X , A , μ ) i ∣ f i ( x ) ∣ ⩽ h ( x ) N i ∈ A x ∈ ( N i ) c ∣ f i ( x ) ∣ ⩽ h ( x ) i → ∞ lim ∫ X ∣ f i − f ∣ d μ = 0. i → ∞ lim ∫ X f i d μ = ∫ X fd μ .
证明. 我们要应用 Beppo Levi 定理. 首先, 定义正函数序列 { g i } i ⩾ 1 g i ( x ) = 2 h ( x ) − k ⩾ i sup ∣ f ( x ) − f k ( x ) ∣. { g i } i ⩾ 1 2 h x ∈ / N i → ∞ lim g i ( x ) = 2 h ( x )
我们考虑集合
N ∪ i ⩾ 1 ⋃ N i , 这是一个零测集. 在
X − N ∪ i ⩾ 1 ⋃ N i 上, 我们有
g i ( x ) ⩾ 0 , g i ( x ) → 2 h ( x ) . 利用 Beppo Levi 定理, 我们知道
i → ∞ lim ∫ X ( 2 h ( x ) − k ⩾ i sup ∣ f ( x ) − f k ( x ) ∣ ) d μ = i → ∞ lim ∫ X g i d μ = 2 ∫ X h d μ . 在方程的两边同时减掉
2 ∫ X h d μ , 我们就得到
i → ∞ lim ∫ X k ⩾ i sup ∣ f ( x ) − f k ( x ) ∣ d μ = 0. 我们只要简单地去掉
sup 就证明了 Lebesgue 控制收敛定理.
在 Lebesgue 控制收敛定理的证明过程中, 我们得到了更强的结论: i → ∞ lim ∫ X k ⩾ i sup ∣ f ( x ) − f k ( x ) ∣ d μ = 0.
下面的两个推论有着众多的应用, 我们会在作业和考试中展现它们:
假定参数空间 Ω Ω R n ( X , A , μ ) f : X × Ω → C , ( x , t ) ↦ f ( x , t ) ,
1)
对每个固定的 t ∈ Ω x ↦ f ( x , t )
2)
对几乎处处的 x t ↦ f ( x , t ) t 0 ∈ Ω N x ∈ N c t ↦ f ( x , t ) t 0 ∈ Ω
3)
存在正函数 h ∈ L 1 ( X , A , μ ) t ∈ Ω ∣ f ( x , t ) ∣ ⩽ h ( x ) x N t x ∈ / N t ∣ f ( x , t ) ∣ ⩽ h ( x )
那么, 函数F : Ω → C , t ↦ F ( t ) = ∫ X f ( x , t ) d μ ( x ) t 0
证明. 由于
∣ f ( x , t ) ∣ ⩽ h ( x ) , 所以对于固定的
t ,
f ( x , t ) 是可积的, 从而函数
F ( t ) 是良好定义的. 我们来证明
F 在
t 0 处的连续性. 为此, 任取点列
t k → t 0 , 我们希望证明
∫ X f ( x , t k ) d μ ( x ) → ∫ X f ( x , t 0 ) d μ ( x ) . 这就是 Lebesgue 控制收敛定理的内容, 因为我们可以选取
h 作为控制函数.