25. 最速降线问题, 积分中值定理

最速降线问题

从点 $(x,f(x))$ 到 $(x+\Delta x,f(x+\Delta x))$ 的距离是 $\sqrt{1+f^{\prime }(x{)}^2}\Delta x$. 根据重力势能到动能的转化 (能量守恒) , 我们知道$$\frac{1}{2}m{v}^2=-mGf(x).$$在 $(x,f(x))$ 处, 小球的速度应该是 $\sqrt{-2Gf(x)}$, 所以从 $(x,f(x))$ 到 $(x+\Delta x,f(x+\Delta x))$ 所需要的时间是$$\Delta t=\frac{\sqrt{1+f^{\prime }(x{)}^2}\Delta x}{\sqrt{-2Gf(x)}}$$这样, 如果曲线 ${\gamma }_s$ 由函数 $f_s(x)=f(x,s)$ 给出, 即$${\gamma }_s:x\in [0,a]\mapsto (x,f_s(x)).$$小球经过整个曲线需要的时间为$$T(s)={\int }_0^a\sqrt{\frac{1+f^{\prime }(x,s{)}^2}{-2Gf(x,s)}}dx.$$其中, $f^{\prime }$ 指的是对 $f(x,s)$ 的 $x$ 变量求导数. 为了保证曲线的两个端点是固定的, 我们还要求$$f(0,s)\equiv 0,f(a,s)\equiv -h.$$对于最速降线 $f_0$ 而言, 我们必然有$$\frac{d}{ds}T(s){|}_{s=0}=0.$$为此, 我们假设 $L(f,f^{\prime })=\sqrt{\frac{1+f^{\prime }(x,s{)}^2}{-2Gf(x,s)}}$, 即在函数$$L(X,V)=\sqrt{\frac{1+V^2}{-2GX}}$$中代换变量 $X=f$, $V=f^{\prime }$. 此时, 我们有 (我们总是假设足够的光滑性使得积分与导数可以交换) : $$\begin{array}{rl}\frac{d}{ds}T(s)& ={\int }_0^a\frac{d}{ds}(L(f_s,f_s^{\prime }))dx\\ & ={\int }_0^a(\frac{dL}{dX})(f_s,f_s^{\prime })\frac{d}{ds}f(x,s)+(\frac{dL}{dV})(f_s,f_s^{\prime })\frac{d}{ds}{f}^{\prime }(x,s)dx\end{array}$$最后一项中, 我们利用两个导数可以交换 (下学期) , 所以 $\frac{d}{ds}{f}^{\prime }(x,s)={\left(\frac{d}{ds}f(x,s)\right)}^{\prime }$. 令 $s=0$ 并记 $f=f_0$, 我们就有$$\begin{array}{rl}\frac{d}{ds}T(s){|}_{s=0}& ={\int }_0^a(\frac{dL}{dX})(f,f^{\prime })\frac{d}{ds}f(x,0)+(\frac{dL}{dV})(f,f^{\prime }){\left(\frac{d}{ds}f(x,s){|}_{s=0}\right)}^{\prime }dx\\ & ={\int }_0^a\left((\frac{dL}{dX})(f,f^{\prime })-\frac{d}{dx}(\frac{dL}{dV})(f,f^{\prime })\right)\frac{df(x,0)}{ds}dx.\end{array}$$最后一步分部积分的过程中, 我们用到了 $f(0,s)\equiv 0$, $f(a,s)\equiv -h$, 从而$$\frac{d}{ds}f(0,s)\equiv 0,\frac{d}{ds}f(a,s)\equiv 0.$$另外, 对任意的函数 $g$ ($g(0)=g(a)=0$) , 我们通过定义 $f(x,s)=f(x)+sg(x)$ 就可以使得$$\frac{d}{ds}f(x,s){|}_{s=0}=g(x).$$所以, 通过选取$$g(x)=\phi (x)[(\frac{dL}{dX})(f,f^{\prime })-\frac{d}{dx}(\frac{dL}{dV})(f,f^{\prime })],$$我们就得到了 $f$ 必须满足的方程 (这被称作是 Euler-Lagrange 方程) : $$(\frac{dL}{dX})(f,f^{\prime })-\frac{d}{dx}\left(\left(\frac{dL}{dV}\right)(f,f^{\prime })\right)=0.$$假设上述方程成立, 那么$$\begin{array}{rl}\frac{d}{dx}\left((V\frac{dL}{dV}-L)(f,f^{\prime })\right)& =\frac{d}{dx}\left(f^{\prime }\frac{dL}{dV}(f,f^{\prime })-L(f,f^{\prime })\right)\\ & =f^{\prime \prime }\frac{dL}{dV}(f,f^{\prime })+f^{\prime }\frac{d}{dx}\left(\frac{dL}{dV}(f,f^{\prime })\right)-f^{\prime }\frac{dL}{dX}(f,f^{\prime })-f^{\prime \prime }\frac{dL}{dV}(f,f^{\prime })\\ & =0.\end{array}$$这表明, 存在常数 $C$, 使得$$(V\frac{dL}{dV}-L)(f,f^{\prime })\equiv C$$按照定义, 我们有$$\frac{dL}{dX}=G\frac{(1+V^2{)}^{\frac{1}{2}}}{(-2GV{)}^{\frac{3}{2}}},\frac{dL}{dV}=\frac{V}{(-2GX(1+V^2){)}^{\frac{1}{2}}}.$$所以, $$\frac{(f^{\prime }{)}^2}{(-2Gf(1+(f^{\prime }{)}^2){)}^{\frac{1}{2}}}-\sqrt{\frac{1+(f^{\prime }{)}^2}{-2Gf}}=C,\iff f(1+(f^{\prime }{)}^2)=-C_1.$$我们令 $f(x)=-g(x)$, 那么, 我们就有$$g^{\prime }(x)=\sqrt{\frac{C_1-g}{g}}$$如果把 $g$ 看作参数, $x=x(g)$, 那么, 根据反函数的导数的计算, 我们有$$\frac{dx}{dg}=\sqrt{\frac{g}{C_1-g}}$$从而, 作为原函数, 我们有$$x(t)=\int \sqrt{\frac{t}{C_1-t}}dt.$$为了能积分出这个函数, 我们做变量替换$$t=C_1{\sin }^2\theta ,$$从而, $$x(\theta )=2C_1\int \tan \theta \cdot \cos \theta \cdot \sin \theta d\theta =C_1(\theta -\frac{1}{2}\sin (2\theta )).$$这样子, 我们就得到了这条曲线的参数方程 (原函数差一个常数 $C_2$) $$\theta \mapsto (\frac{C_1}{2}(2\theta -\sin (2\theta ))+C_2,-\frac{C_1}{2}(1-\cos (2\theta )))$$重新参数化之后, 我们得到一条曲线$$\gamma :[{\theta }_1,{\theta }_2]\to {\mathbb{R}}^2,\theta \mapsto (c(\theta -\sin \theta )+C,-c(1-\cos \theta ))$$这种曲线叫做被称作是摆线或者旋轮线. 我们注意到, 初始时刻 $y({\theta }_1)=0$, 所以, $\cos {\theta }_1=1$, 这表明 ${\theta }_1=2k\pi$, $C=-2ck\pi$, 通过再次调整 $\theta \mapsto \theta -2k\pi$, 我们可以假设 ${\theta }_1=0$, $C=0$, 所以我们要找的参数曲线为$$\gamma :[0,\Theta ]\to {\mathbb{R}}^2,\theta \mapsto (c(\theta -\sin \theta ),-c(1-\cos \theta ))$$从而, $$c(\Theta -\sin \Theta )=a,-c(1-\cos \Theta )=-h$$可以确定 $\Theta \in [0,\frac{\pi }{2}]$ 和 $c$.

命题 25.1 (等时性, Huygens). 考虑摆线$$\gamma :[0,\frac{\pi }{2}]\to {\mathbb{R}}^2,\theta \mapsto (c(\theta -\sin \theta ),-c(1-\cos \theta )).$$

那么, 从任意一点 $\gamma ({\theta }_0)$ 出发的小球滚动到 $\gamma (\pi )=(c\pi ,-2c)$ 的时间都是一样的.

证明. 实际上, 小球在 $\gamma (\theta )$ 到 $\gamma (\theta +\Delta \theta )$ 处要经过的距离为: $$\Delta =|{\gamma }^{\prime }(\theta )|\Delta \theta =c\sqrt{2-2\cos \theta }\Delta \theta$$小球的速度为: $$v=\sqrt{2Gc(\cos {\theta }_0-\cos \theta )}.$$所以, 从 $\gamma ({\theta }_0)$ 滑到底一共需要$$\begin{array}{rl}T({\theta }_0)& =\sqrt{\frac{c}{G}}{\int }_{{\theta }_0}^{\pi }\sqrt{\frac{1-\cos \theta }{\cos {\theta }_0-\cos \theta }}d\theta \\ & =\sqrt{\frac{c}{G}}{\int }_{{\theta }_0}^{\pi }\frac{\sin \left(\frac{\theta }{2}\right)}{\sqrt{{\cos }^2\left(\frac{{\theta }_0}{2}\right)-{\cos }^2\left(\frac{\theta }{2}\right)}}d\theta \end{array}$$我们可以令 $s=\cos \left(\frac{\theta }{2}\right)$ 进行换元积分, 据此, 得到 $T({\theta }_0)\equiv \pi \sqrt{\frac{c}{G}}$.

$\square$

积分中值定理

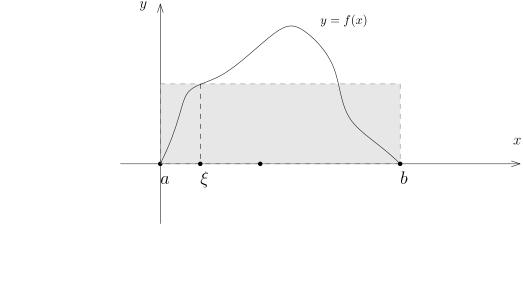
定理 25.2 (第一积分中值定理). $[a,b]$ 是有界闭区间, $f,g\in \mathcal{R}([a,b])$ 是实值 Riemann 可积函数. 我们假设对任意的 $x\in [a,b]$, $g(x)⩾0$. 令$$m=\underset{x\in I}{\inf }f(x),M=\underset{x\in I}{\sup }f(x).$$那么, 存在 $\ell \in [m,M]$, 使得$${\int }_a^{b}fg=\ell {\int }_a^{b}g.$$特别地, 如果进一步要求 $f$ 是连续函数, 那么存在 $\xi \in [a,b]$, 使得$${\int }_a^{b}fg=f(\xi ){\int }_a^{b}g.$$

证明. 由于 $m⩽f(x)⩽M$, 根据 $g⩾0$ 以及积分保持不等号的性质, 我们有$$m{\int }_a^{b}g⩽{\int }_a^{b}fg⩽M{\int }_a^{b}g.$$如果 ${\int }_a^{b}g\ne 0$, 显然存在 $\ell \in [m,M]$ 使得命题成立; 如果 ${\int }_a^{b}g=0$, 由于 $g⩾0$, 所以 $g$ 在一个零测集之外恒为 $0$, 从而 $fg$ 在一个零测集之外都是 $0$, 从而 ${\int }_a^{b}fg=0$, 所以 $\ell$ 可以任意选.

如果 $f$ 是连续的, 所以 $f$ 在 $[a,b]$ 可以取到最大值 $M$ 和最小值 $m$, 即有 $x_1,x_2\in [a,b]$, 使得 $f(x_1)=m$, $f(x_2)=M$, 根据连续函数的中值定理, 存在 $x_1$ 与 $x_2$ 之间的数 $\xi$, 使得 $f(\xi )=\ell$.

$\square$

推论 25.3. 假设 $f$ 是连续函数, 那么存在 $\xi \in [a,b]$, 使得 ${\int }_a^{b}f=f(\xi )(b-a)$.

证明. 只要取 $g\equiv 1$ 即可.

$\square$