75. 有界区域上 Sobolev 空间的扩张与限制至子流形

我们现在给出 Sobolev 函数的局部刻画. 假设 $\Omega$ 是有界光滑带边的区域 ($\overline{\Omega }$ 是紧集) , $\mathcal{U}=\{U_j{\}}_{j⩽N}$ 是 $\overline{\Omega }$ 的一个开覆盖, $\{{\chi }_j{\}}_{j⩽N}$ 是相应的一族单位分解.

命题 75.1. 给定 $u\in {\mathcal{D}}^{\prime }(\Omega )$, 那么如下等价:

1)	$u\in H^1(\Omega )$;
2)	对任意的 $j⩽N$, ${\chi }_j\cdot u\in H^1(\Omega )$.

证明. 先证明 $1)\Rightarrow 2)$: 很明显, 我们有$$\Vert {\chi }_{j}u{\Vert }_{L^2}⩽C\Vert u{\Vert }_{L^2},$$根据分布求导的 Leibniz 公式, 我们有$$\Vert \nabla ({\chi }_{j}u){\Vert }_{L^2}=\Vert (\nabla {\chi }_j)u+{\chi }_j\nabla u{\Vert }_{L^2}⩽C\left(\Vert u{\Vert }_{L^2}+\Vert \nabla u{\Vert }_{L^2}\right).$$所以, 这个方向是成立的.

再证明 $2)\Rightarrow 1)$: 由于$$u=\sum _{j⩽N}{\chi }_j\cdot u,$$是有限个 $H^1(\Omega )$ 中元素的线性组合, 所以落在 $H^1(\Omega )$ 中.

$\square$

注记. 这个命题对于空间 $H_0^1(\Omega )$ 也成立: 假设 $\{{\phi }_p{\}}_{p⩾1}\subset C_0^{\infty }(\Omega )$, 使得 $\underset{p\to \infty }{\lim }{\phi }_p\stackrel{H^1}{=}u$, 那么, $$\underset{p\to \infty }{\lim }{\chi }_j\cdot {\phi }_p\stackrel{H^1}{=}{\chi }_j\cdot u.$$证明是平凡的.

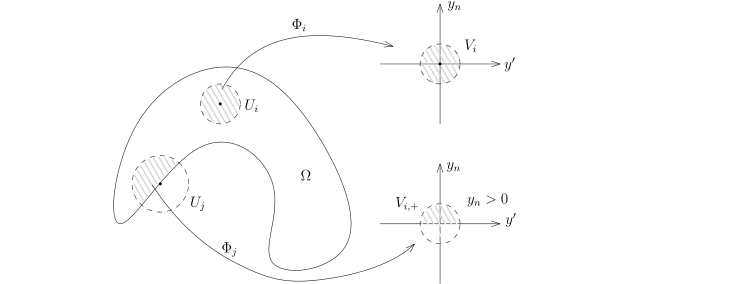
对于 $x\in \overline{\Omega }$, 我们选取包含 $x$ 的一个开的小球 $U$, 这些开集覆盖了 $\overline{\Omega }$. 对于 $x\in \partial \Omega$, 我们要求 $U$ 选取的足够小, 使得存在微分同胚$$\Phi :U\to V\subset {\mathbb{R}}^{n-1}\times \mathbb{R},x\mapsto (y^{\prime },y_n)=({\Phi }^{\prime }(x),{\Phi }_n(x)),$$其中, $V$ 是 ${\mathbb{R}}_y^n$ 中的开球, 并且

•	$\Phi (U\cap \Omega )=V_{+}=V\cap \{y^{\prime },y_n)|y_n>0\}$;
•	$\Phi (x)$ 的 $y_n$ 坐标是 $0$.

此时, $\Phi (U\cap \partial \Omega )\subset \{y_n=0\}$ 被实现为 ${\mathbb{R}}^n$ 的超平面.

从这些开集中, 我们可以选取 $\overline{\Omega }$ 的一个有限开覆盖 $\{U_j{\}}_{j⩽N}$, 与之对应的 $\Phi$ 我们记做是 ${\Phi }_j$. 我们注意到, 这些 $U_j$ 们分两种, 一种是边界点给出的, 另一种是内点给出的 (与边界不相交) .

利用与 $\{U_j{\}}_{j⩽N}$ 相适应的单位分解 $\{{\chi }_j{\}}_{j⩽N}$, 对任意的 $u\in H^1(\Omega )$ 和 $u_0\in H_0^1(\Omega )$, 我们知道 ${\chi }_j\cdot u\in H^1(\Omega )$, ${\chi }_j\cdot u_0\in H_0^1(\Omega )$, 通过复合, 我们得到了 $({\chi }_j\cdot u)\circ {\Phi }_j^{-1}$ 和 $({\chi }_j\cdot u_0)\circ {\Phi }_j^{-1}$, 这都是 $V_j$ 或者 $V_{j,+}$ 上的函数. 我们不妨研究 $u$ 和 $V_{j,+}$ 的情形 (其余类似) . 我们现在来说明$$({\chi }_j\cdot u)\circ {\Phi }_j^{-1}\in H^1(V_{j,+}).$$以下我们用 $U_{j,+}$ 表示 $U_j\cap \Omega$. 根据换元积分公式, 我们有$${\int }_{V_{j,+}}{\left|({\chi }_j\cdot u)\circ {\Phi }_j^{-1}(y)\right|}^{2}dy={\int }_{U_{j,+}}{\left|({\chi }_j\cdot u)(x)\right|}^2|\mathrm{Jac}({\Phi }_j)(x)|dx.$$由于上述 Jacobi 行列式是有界的, 所以$${\int }_{V_{j,+}}{\left|({\chi }_j\cdot u)\circ {\Phi }_j^{-1}(y)\right|}^{2}dy⩽C{\int }_{U_{j,+}}{\left|({\chi }_j\cdot u)(x)\right|}^{2}dx.$$另外, 根据链式求导公式, 我们有$$\left|{\partial }_k\left(({\chi }_j\cdot u)\circ {\Phi }_j^{-1}(y)\right)\right|=\left|\sum _{\ell ⩽n}{\partial }_{\ell }({\chi }_j\cdot u)\cdot {\partial }_k\left({\Phi }_j^{-1}{}_{\ell }\right)\right|⩽C\left|\nabla ({\chi }_j\cdot u)\right|.$$所以, 重复上面的计算就知道$${\int }_{V_{j,+}}{\left|\nabla \left(({\chi }_j\cdot u)\circ {\Phi }_j^{-1}(y)\right)\right|}^{2}dy⩽C{\int }_{U_{j,+}}{\left|\nabla ({\chi }_j\cdot u)(x)\right|}^{2}dx.$$综合上面的不等式, 实际上我们证明了$$({\chi }_j\cdot u)\circ {\Phi }_j^{-1}\in H^1(V_{j,+})\iff {\chi }_j\cdot u\in H^1(U_{j,+}).$$

通过限制, 显然有连续线性映射$$\mathrm{Res}:H^1\left({\mathbb{R}}^n\right)\to H^1\left(\Omega \right).$$利用上述关于 Sobolev 函数的局部描述, 我们可以构造扩张映射:

引理 75.2 (从 $H^1(\Omega )$ 到 $H^1({\mathbb{R}}^n)$ 扩张). 限制映射$$\mathrm{Res}:H^1\left({\mathbb{R}}^n\right)\to H^1\left(\Omega \right)$$是连续的满的线性映射击并且存在连续线性的扩张映射$$\mathrm{Ext}:H^1\left(\Omega \right)\to H^1\left({\mathbb{H}}^n\right)$$使得$$\mathrm{Res}\circ \mathrm{Ext}={\mathrm{id}}_{H^1(\Omega )}.$$

注记. 上述扩张映射未必是唯一的, 它依赖于局部坐标描述的选取等等, 请参考证明.

证明. 我们把上述构造的覆盖 $\mathcal{U}=\{U_j{\}}_{j⩽N}$ 分成两个部分$$\mathcal{U}={\mathcal{U}}^{\prime }\cup {\mathcal{U}}^{\prime \prime }=\{U_{j^{\prime }}^{\prime }{\}}_{j^{\prime }⩽N^{\prime }}\cup \{U_{j^{\prime \prime }}^{\prime \prime }{\}}_{j^{\prime \prime }⩽N^{\prime \prime }}.$$其中, ${\mathcal{U}}^{\prime }$ 中的开集和边界不相交, ${\mathcal{U}}^{\prime \prime }$ 中的开集和边界相交. 那么, 对任意的 $u\in H^1(\Omega )$, 我们有$$u=\sum _{j^{\prime }⩽N^{\prime }}{\chi }_{j^{\prime }}^{\prime }u+\sum _{j^{\prime \prime }⩽N^{\prime \prime }}{\chi }_{j^{\prime \prime }}^{\prime \prime }u.$$我们只要能对每个 ${\chi }_{j^{\prime }}^{\prime }u$ 和 ${\chi }_{j^{\prime \prime }}^{\prime \prime }u$ 进行延拓即可.

首先, 由于 ${\chi }_{j^{\prime }}^{\prime }u$ 的支集在 $\Omega$ 中, 所以我们用 $0$ 进行延拓即可. 下面研究 ${\chi }_{j^{\prime \prime }}^{\prime \prime }u$, 为了书写简洁, 我们仍然用 ${\chi }_{j}u$ 表示这个函数, 那么, $$v_j=({\chi }_{j}u)\circ {\Phi }_j^{-1}\in H^1(V_{j,+}).$$在构造这些覆盖的时候, 我们总是可以要求 $V_j$ 是对称的, 即 $V_j=V_{j,+}\cup \left(-V_{j,+}\right)$. 对于 $v_j$ 而言, 我们可以用之前构造的对称的扩张 ${\mathrm{Ext}}_{{}_{\mathrm{sym}}}(v_j)$. 此时, 由于 $\mathrm{supp}(v_j)\subset V_{j,+}$, 所以, $$\mathrm{supp}\left({\mathrm{Ext}}_{{}_{\mathrm{sym}}}(v_j)\right)\subset V_j={\Phi }_j(U_j)$$并且是 $H^1$ 的函数. 那么, $$\widetilde{u_j}=\left({\mathrm{Ext}}_{{}_{\mathrm{sym}}}(v_j)\right)\circ {\Phi }_j^{-1}$$是支集在 $U_j$ 中的具有紧支集的 $H^1(U_j)$ 中的函数, 我们可以再把它延拓到 ${\mathbb{R}}^n$ 上去.

由于上述的覆盖是事先选定的, 所以, 上述构造的算子是线性的 (每一步都是确定的) .

$\square$

作为推论, 我们有

推论 75.3 (用全空间上的光滑函数逼近的 $H^1(\Omega )$). 对任意的 $u\in H^1(\Omega )$, 存在 $\{\phi {\}}_{k⩾1}\subset C_0^{\infty }({\mathbb{R}}^n)$, 使得 $u$ 可以被 $\{{\phi }_k{|}_{\Omega }{\}}_{k⩾1}$ 逼近: $$\underset{k\to \infty }{\lim }{\Vert {\phi }_k{|}_{\Omega }-u\Vert }_{H^1(\Omega )}=0.$$

证明. 首先, 在全空间中, 我们能够找到 $\{\phi {\}}_{k⩾1}\subset C_0^{\infty }({\mathbb{R}}^n)$, 使得$$\underset{k\to \infty }{\lim }{\Vert {\phi }_k-\mathrm{Ext}(u)\Vert }_{H^1({\mathbb{R}}^n)}=0.$$所以, $$\underset{k\to \infty }{\lim }{\Vert {\phi }_k{|}_{\Omega }-\mathrm{Ext}(u){|}_{\Omega }\Vert }_{H^1(\Omega )}=0.$$而 $\mathrm{Ext}(u){|}_{\Omega }=u$, 这就给出了证明.

$\square$

我们现在来定义 $H^{\frac{1}{2}}(\partial \Omega )$ 空间.

一种可行的方式是利用局部覆盖: 我们上面构造了一族关于 $\overline{\Omega }$ 的覆盖, 我们现在只考虑那些和 $\partial \Omega$ 相交的覆盖, 不妨还记作是 $\mathcal{U}=\{U_j{\}}_{j⩽N}$, 那么, 对每个 $j⩽N$, 我们有微分同胚$${\varphi }_j:U_j\cap (\partial \Omega )\to V^{\prime }\subset {\mathbb{R}}^{n-1}.$$这是之前的 ${\Phi }_j$ 在 $U_j\cap \partial \Omega$ 上的限制. 假设 $u\in L^2(\partial \Omega )$, 利用与 $\mathcal{U}$ 相适应的单位分解 $\{{\chi }_j{\}}_{j⩽}$, 我们就有$$u=\sum _{j⩽N}{\chi }_j\cdot u=\sum _{j⩽N}{u}_j,$$其中 $\mathrm{supp}(u_j)\subset U_j\cap \partial \Omega$.

那么, 当我们说 $u\in H^{\frac{1}{2}}(\partial \Omega )$ 指的是对任意的 $j⩽N$, 函数 $u_j\circ {\varphi }_j^{-1}$ 作为 $V_j^{\prime }$ 上的函数是 $H^{\frac{1}{2}}$ 的, 这里, 因为 $\mathrm{supp}(u_j\circ {\varphi }_j^{-1})\subset V_j^{\prime }$, 所以, 我们可以通过延拓把 $u_j\circ {\varphi }_j^{-1}$ 看作是 ${\mathbb{R}}^{n-1}$ 上的函数, 这就可以谈论 $u_j\circ {\varphi }_j^{-1}$ 是否是 $H^{\frac{1}{2}}$ 的. 在此基础上, 我们定义$$\Vert u{\Vert }_{H^{\frac{1}{2}}(\partial \Omega ),\mathcal{U}}=\sum _{j⩽N}\Vert u_j\circ {\varphi }_j^{-1}{\Vert }_{H^{\frac{1}{2}}({\mathbb{R}}^{n-1})}.$$当然, 这样定义的 $\Vert u{\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}$ 依赖于覆盖 $\mathcal{U}$ 以及单位分解的选取. 我们不难证明 (习题) , 如果采取另一种覆盖 $\mathcal{U}$ 和单位分解, 新定义出来的范数与这种定义是等价的, 所以, 它们所定义的收敛 (拓扑) 概念是一致的.

我们现在采取另一种方式来定义 $H^{\frac{1}{2}}(\partial \Omega )$ 并且证明上面定义的范数与将要定义的范数是等价的 (这就给出了 $\Vert u{\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}$ 不依赖于覆盖 $\mathcal{U}$ 以及单位分解的选取的一种证明) . 这个定义依赖于我们已经证明过的命题: 当 Sobolev 指标 $0<s<1$ 时, $u\in L^2({\mathbb{R}}^n)$, 那么 $u\in H^s({\mathbb{R}}^n)$ 当且仅当$$\int {\int }_{{\mathbb{R}}^n\times {\mathbb{R}}^n}\frac{|u(x)-u(y){|}^2}{|x-y{|}^{n+2s}}dxdy<\infty .$$其中, 我们$$\Vert u{\Vert }_{H^s({\mathbb{R}}^n)}^2\approx \Vert u{\Vert }_{L^2({\mathbb{R}}^n)}^2+\int {\int }_{{\mathbb{R}}^n\times {\mathbb{R}}^n}\frac{|u(x)-u(y){|}^2}{|x-y{|}^{n+2s}}dxdy.$$

定义 75.4. 我们用 $d\sigma$ 表示 $\partial \Omega$ 上的曲面测度. 对于任意的 $u\in L^2(\partial \Omega )$, 如果如下的积分是有限的 (注意到 $\dim \partial \Omega =n-1$) : $$\int {\int }_{\partial \Omega \times \partial \Omega }\frac{|u(x)-u(y){|}^2}{|x-y{|}^n}d\sigma (x)d\sigma (y)<\infty ,$$我们就说 $u\in H^{\frac{1}{2}}(\partial \Omega )$. 对于 $u\in H^{\frac{1}{2}}(\partial \Omega )$, 我们定义范数$$\Vert u{\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}^2=\Vert u{\Vert }_{L^2(\partial \Omega )}^2+\int {\int }_{\partial \Omega \times \partial \Omega }\frac{|u(x)-u(y){|}^2}{|x-y{|}^n}d\sigma (x)d\sigma (y).$$我们可以很容易地验证三角不等式, 从而, 我们得到了一个范数.

对任意的 $\delta >0$, 很明显, 这个范数的定义等价于$$\Vert u{\Vert }_{H^{\frac{1}{2}}(\partial \Omega ),\delta }^2=\Vert u{\Vert }_{L^2(\partial \Omega )}^2+\int {\int }_{\partial \Omega \times \partial \Omega }\frac{|u(x)-u(y){|}^2}{|x-y{|}^n}{1}_{|x-y|<\delta }d\sigma (x)d\sigma (y).$$(差一个大约是 ${\delta }^{-(n+1)}$ 的常数)

利用单位分解我们还可以定义这种范数的局部版本: $$\text{vertiii}{u}_{H^{\frac{1}{2}}(\partial \Omega ),\mathcal{U}}^2=\sum _{j⩽N}\Vert {\chi }_j\cdot u{\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}^2,$$我们首先证明 $\text{vertiii}{\cdot }_{H^{\frac{1}{2}}(\partial \Omega ),\mathcal{U}}$ 与范数 $\Vert \cdot {\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}$ 是等价的.

我们选取 $\partial \Omega$ 的开覆盖 $\mathcal{U}$, 我们要求对任意的 $U\in \mathcal{U}$, 都有 $\mathrm{diam}(U)<\frac{1}{2}\delta$ (直径) . 此时, 我们有$$\Vert u{\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}^2⩽\sum _{j⩽N}\Vert {\chi }_j\cdot u{\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}^2.$$另外, $$\begin{array}{rl}& \int {\int }_{\partial \Omega \times \partial \Omega }\frac{|{\chi }_j(x)u(x)-{\chi }_j(y)u(y){|}^2}{|x-y{|}^n}d\sigma (x)d\sigma (y)\\ ⩽& 2\int {\int }_{\partial \Omega \times \partial \Omega }\frac{|{\chi }_j(x){|}^2|u(x)-u(y){|}^2}{|x-y{|}^n}d\sigma (x)d\sigma (y)+2\int {\int }_{\partial \Omega \times \partial \Omega }\frac{|{\chi }_j(x)-{\chi }_j(y){|}^2}{|x-y{|}^n}|u(y){|}^{2}d\sigma (x)d\sigma (y)\\ ⩽& 2\int {\int }_{\partial \Omega \times \partial \Omega }\frac{|u(x)-u(y){|}^2}{|x-y{|}^n}d\sigma (x)d\sigma (y)+C\int {\int }_{\partial \Omega \times \partial \Omega }\frac{1}{|x-y{|}^{n-2}}|u(y){|}^{2}d\sigma (x)d\sigma (y).\end{array}$$在上面的估计中, 根据 Lagrange 中值定理, 我们用 $C|x-y|$ 来控制了 ${\chi }_j(x)-{\chi }_j(y)$ (这里用到了截断函数的光滑性, $u$ 没有这种光滑性) .

所以, $$\Vert {\chi }_j\cdot u{\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}^2⩽C\Vert u{\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}^2+C{\int }_{\partial \Omega }|u(y){|}^2\left({\int }_{\partial \Omega }\frac{1}{|x-y{|}^{n-2}}d\sigma (x)\right)d\sigma (y).$$

练习. 证明, 存在常数 $C$, 使得对任意的 $y$, 我们都有$${\int }_{\partial \Omega }\frac{1}{|x-y{|}^{n-2}}d\sigma (x)⩽C.$$

据此, $$\Vert {\chi }_j\cdot u{\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}⩽C\Vert u{\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}^2.$$因此范数 $\text{vertiii}{\cdot }_{H^{\frac{1}{2}}(\partial \Omega ),\mathcal{U}}$ 与范数 $\Vert \cdot {\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}$ 是等价的. 我们下面说明它们都与下面已经定义的范数等价: $$\Vert u{\Vert }_{H^{\frac{1}{2}}(\partial \Omega ),\mathcal{U}}=\sum _{j⩽N}\Vert u_j\circ {\varphi }_j^{-1}{\Vert }_{H^{\frac{1}{2}}({\mathbb{R}}^{n-1})}.$$

为此, 只要对任意的 $j$, 证明$$\Vert u_j\circ {\varphi }_j^{-1}{\Vert }_{H^{\frac{1}{2}}({\mathbb{R}}^{n-1})}\approx \Vert u_j{\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}$$即可. 这里, $\mathrm{supp}(u_j)\subset U_j\cap \Omega$ 是紧的. 通过将覆盖加细, 我们总是可以假设局部上 $\partial \Omega$ 是函数的图像.

我们利用微分同胚$${\varphi }_j:U_i\cap (\partial \Omega )\to V^{\prime }\subset {\mathbb{R}}^{n-1}.$$其中, ${\varphi }_j$ 是 ${\Phi }_j$ 在 $\partial \Omega$ 上的限制. 实际上, 我们有$$\begin{array}{rl}\Vert u_j{\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}^2& =\int {\int }_{{\varphi }_j^{-1}(V^{\prime })\times {\varphi }_j^{-1}(V^{\prime })}\frac{|u_j(x)-u_j(x^{\prime }){|}^2}{|x-x^{\prime }{|}^n}d\sigma (x)d\sigma (x^{\prime })\\ & \approx \int {\int }_{V^{\prime }\times V^{\prime }}\frac{{\left|\left(u_j\circ {\varphi }_j^{-1}\right)(y)-\left(u_j\circ {\varphi }_j^{-1}\right)(y^{\prime })\right|}^2}{{\left|{\varphi }_j^{-1}(y)-{\varphi }_j^{-1}(y^{\prime })\right|}^n}dyd{y}^{\prime }\end{array}$$在上一个约等于号中, 我们实际上先把测度用函数图像的形式表达, 然后利用再乘上坐标变换的 Jacobi 矩阵. 这些操作只是在 $dy$ 之前乘了一个上下有界的正的函数, 所以我们有上面的约等于号. 另外, 由于 ${\varphi }_j^{-1}$ 是微分同胚, 所以$$\left|{\varphi }_j^{-1}(y)-{\varphi }_j^{-1}(y^{\prime })\right|\approx \left|y-y^{\prime }\right|.$$据此, 我们知道$$\Vert u_j{\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}^2\approx \int {\int }_{V^{\prime }\times V^{\prime }}\frac{{\left|\left(u_j\circ {\varphi }_j^{-1}\right)(y)-\left(u_j\circ {\varphi }_j^{-1}\right)(y^{\prime })\right|}^2}{{\left|y-y^{\prime }\right|}^{n-1+2\times \frac{1}{2}}}dyd{y}^{\prime }\approx \Vert u_j\circ {\varphi }_j^{-1}{\Vert }_{H^{\frac{1}{2}}({\mathbb{R}}^{n-1})}.$$这就证明了两个范数的等价性.

特别地, 我们利用范数$$\Vert u{\Vert }_{H^{\frac{1}{2}}(\partial \Omega ),\mathcal{U}}=\sum _{j⩽N}\Vert ({\chi }_j\cdot u)\circ {\varphi }_j^{-1}{\Vert }_{H^{\frac{1}{2}}({\mathbb{R}}^{n-1})},$$可以很方便地证明 $H^{\frac{1}{2}}(\partial \Omega )$ 的完备性: 假设 $\{u_p{\}}_{p⩾1}\subset H^{\frac{1}{2}}(\partial \Omega )$ 是 Cauchy 列, 那么, 按照定义, 对任意的 $j⩽N$, $\{({\chi }_j\cdot u_p)\circ {\varphi }_j^{-1}{\}}_{p⩾1}\subset H^{\frac{1}{2}}({\mathbb{R}}^{n-1})$ 是 Cauchy 列, 所以, 对每个 $j$, 存在具有紧支集的 $v_j\in H^{\frac{1}{2}}(V^{\prime })$, 使得$$\underset{p\to \infty }{\lim }{\Vert ({\chi }_j\cdot u_p)\circ {\varphi }_j^{-1}-v_j\Vert }_{H^{\frac{1}{2}}({\mathbb{R}}^{n-1})}=0.$$我们令$$u=\sum _{j⩽N}{v}_j\circ {\varphi }_j.$$利用 $\Vert \cdot {\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}$ 这个范数, 很明显每个 $v_j\circ {\varphi }_j$ 都落在 $H^{\frac{1}{2}}(\partial \Omega )$ 中, 所以, $u\in H^{\frac{1}{2}}(\partial \Omega )$. 仍然利用这个范数, 我们就有$$\begin{array}{rl}\Vert u_p-u{\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}& ⩽\sum _{j⩽N}\Vert {\chi }_j\cdot u_p-v_j\circ {\varphi }_j{\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}\\ & \approx \sum _{j⩽N}\Vert \left({\chi }_j\cdot u_p\right)\circ {\varphi }_j^{-1}-v_j{\Vert }_{H^{\frac{1}{2}}({\mathbb{R}}^{n-1})}\to 0\end{array}$$从而, 我们证明了

命题 75.5. 函数空间 $\left(H^{\frac{1}{2}}(\Omega ),\Vert \cdot {\Vert }_{H^{\frac{1}{2}(\Omega )}}\right)$ 是完备内积空间, 其中, 我们用如下物理空间上的内积$${\left(u_1,u_2\right)}_{H^{\frac{1}{2}}(\partial \Omega )}^2=(u_1,u_2{)}_{L^2(\partial \Omega )}+\int {\int }_{\partial \Omega \times \partial \Omega }\frac{\left(u_1(x)-u_2(y)\right)\left(\overline{u_1(x)}-\overline{u_2(y)}\right)}{|x-y{|}^n}d\sigma (x)d\sigma (y).$$其中, $u_1,u_2\in H^{\frac{1}{2}}(\Omega )$.

我们现在来定义限制 (迹) 映射:

定理 75.6. 假设 $n⩾1$, $\Omega \subset {\mathbb{R}}^n$ 是有界带边区域. 那么, 限制映射$$\mathrm{Res}:\mathcal{D}({\mathbb{R}}^n)⟶C^{\infty }(\partial \Omega )$$可以唯一地延拓成连续线性映射$$\mathrm{Res}:H^1(\Omega )⟶H^{\frac{1}{2}}(\partial \Omega )$$使得如下的图表是交换的: $$0\to H_0^1(\Omega )\stackrel{\iota }{⟶}{H}^1(\Omega )\stackrel{\mathrm{Res}}{⟶}{H}^{\frac{1}{2}}\left(\partial \Omega \right)\to 0,$$也就是说 $\mathrm{Res}$ 是满射并且对任意的 $u\in H^1(\Omega )$, $\mathrm{Res}(u)=0$ 当且仅当 $u\in H_0^1(\Omega )$.

证明. 由于我们之前已经证明了 $\mathcal{D}({\mathbb{R}}^n)\cap H^1(\Omega )$ 是 $H^1(\Omega )$ 的稠密子空间, 所以, 我们只要证明存在常数 $C>0$, 使得对任意的光滑函数 $u\in \mathcal{D}({\mathbb{R}}^n)$, 我们有如下的不等式$$\Vert u{|}_{\partial \Omega }{\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}⩽C\Vert u{\Vert }_{H^1(\Omega )}.$$首先, 利用单位分解, 我们把 $u$ 写成$$u=\sum _{j⩽N}{\chi }_j\cdot u=\sum _{j⩽N}{u}_j.$$如果 $\mathrm{supp}(u_j)\cap \partial \Omega =\varnothing$, 那么它对限制映射没有贡献. 所以, 我们可以假设所有的 $\mathrm{supp}(u_j)$ 都与边界相交. 对于一个特定的 $u_j$, 我们知道$$u_j{|}_{\partial \Omega }\circ {\varphi }_j^{-1}=\left(u_j\circ {\Phi }_j\right){|}_{y_n=0}.$$所以, $$\begin{array}{rl}\Vert u_j{|}_{\partial \Omega }{\Vert }_{H^{\frac{1}{2}}(\partial \Omega )}& =\Vert u_j{|}_{\partial \Omega }\circ {\varphi }_j^{-1}{\Vert }_{H^{\frac{1}{2}}({\mathbb{R}}^{n-1})}=\Vert \left(u_j\circ {\Phi }_j\right){|}_{y_n=0}{\Vert }_{H^{\frac{1}{2}}({\mathbb{R}}^{n-1})}\\ & ⩽C\Vert u_j\circ {\Phi }_j{\Vert }_{H^1({\mathbb{H}}^n)}⩽C^{\prime }\Vert u_j{\Vert }_{H^1(\Omega )}⩽C^{\prime \prime }\Vert u{\Vert }_{H^1(\Omega )}.\end{array}$$对 $j$ 求和, 我们就得到了要证明的不等式. 特别地, 这就构造了连续的限制映射$$\mathrm{Res}:H^1(\Omega )⟶H^{\frac{1}{2}}(\partial \Omega ).$$正合列的单射部分是平凡的, 我们现在证明如果 $\mathrm{Res}(u)=0$, 那么 $u\in H_0^1(\Omega )$: 实际上, 我们有$$\mathrm{Res}({\chi }_j\cdot u)={\chi }_j\mathrm{Res}(u)=0.$$所以, 只要对 $u_j$ 证明即可. 此时, 考虑 $u_j\circ {\Phi }_j^{-1}$, 它可以被 $\{{\phi }_p{\}}_{p⩾1}\subset C_0^{\infty }({\mathbb{H}}^n)$ 在 $H^1({\mathbb{H}}^n)$ 中逼近, 所以, $\{{\phi }_p\circ {\Phi }_j{\}}_{p⩾1}$ 在 $H^1(\Omega )$ 中逼近 $u_j$. 这说明 $u_j\in H_0^1(\Omega )$, 所以, $$u=\sum _{j⩽N}{u}_j\in H_0^1(\Omega ).$$最后一个关于 $\mathrm{Res}$ 的满射性也可以同样的证明: 对任意的 $f\in H^{\frac{1}{2}}(\Omega )$, 我们把它写成$$f=\sum _{j⩽N}{\chi }_j\cdot f=\sum _{j⩽N}{f}_j.$$我们只要对任意的 $j$, 找到一个 $u_j\in H^1(\Omega )$, 使得 $u_j{|}_{\partial \Omega }=f_j$ 即可.

由于 $f_j\in H^{\frac{1}{2}}(\partial \Omega \cap U_j)$, 我们要转化到 $V_j^{+}$ 上考虑问题, 那么, $f_j\circ {\varphi }_j^{-1}\in H^{\frac{1}{2}}(V_j)$. 根据半空间上的限制定理, 我们知道存在 $u\in H^1(V_j)$ 并且 $\mathrm{supp}(u)\in H^1(V_j)$, 使得 $u{|}_{y_n=0}=f_j\circ {\varphi }_j^{-1}$, 所以, $u_j=u\circ {\Phi }_j$ 即为所求.

$\square$

这个定理的证明可以原封不动地用来证明:

定理 75.7. 假设 $n⩾1$, $k⩾1$ 是整数, $\Omega \subset {\mathbb{R}}^n$ 是有界带边区域. 那么, 限制映射$$\mathrm{Res}:\mathcal{D}({\mathbb{R}}^n)⟶C^{\infty }(\partial \Omega )$$可以唯一地延拓成连续线性映射$$\mathrm{Res}:H^k(\Omega )⟶H^{k-\frac{1}{2}}(\partial \Omega )$$我们还有如下的正合列: $$0\to H_0^k(\Omega )\stackrel{\iota }{⟶}{H}^k(\Omega )\stackrel{\mathrm{Res}}{⟶}{H}^{k-\frac{1}{2}}\left(\partial \Omega \right)\to 0.$$