Riemann 积分的性质 给定有界闭区间 [ a , b ] C ( [ a , b ] ) R ( [ a , b ] ) C ( [ a , b ] ) ∥ ⋅ ∥ ∞ ∥ f ∥ ∞ = x ∈ [ a , b ] sup ∣ f ( x ) ∣. ∫ a b : C ( [ a , b ] ) ⟶ R , f ↦ ∫ a b f . f , g ∈ C ( [ a , b ] ) ∣ ∣ ∫ a b f − ∫ a b g ∣ ∣ ⩽ ∫ a b ∣ f − g ∣ ⩽ ∫ a b ∥ f − g ∥ ∞ = ( b − a ) d ∞ ( f , g ) . f n → f C ( [ a , b ] ) n → ∞ lim ∫ a b f n = ∫ a b f .
存在 f n , f ∈ C ( [ a , b ] ) x ∈ [ a , b ] n → ∞ f n ( x ) → f ( x ) n → ∞ lim ∫ a b f n = ∫ a b f .
我们上一次课证明了关于 Riemann 积分的 Lebesgue 定理: f ∈ R ( [ a , b ] ) f
f : I → J ⊂ R g : J → R V g ∘ f f : I → C ∣ f ( x ) ∣ ⩾ δ > 0 f 1
证明. 这是因为如果 f x 0 g ∘ f x 0 g ∘ f f
对于
f : I → C , 我们按照实部和虚部分解, 有
f = f 1 + i f 2 , 此时,
f 1 和
f 2 都是可积的. 那么
f 1 = ( f 1 ) 2 + ( f 2 ) 2 f 1 − i ( f 1 ) 2 + ( f 2 ) 2 f 2 , 是可积的.
f : [ a , b ] → R ⩾ 0 ∫ a b f = 0 { x ∈ [ a , b ] ∣ f ( x ) = 0 }
证明. 如果 ∫ a b f = 0 { x ∈ [ a , b ] ∣ ∣ f ( x ) = 0 } x 0 f ( x 0 ) = 0 { x ∈ [ a , b ] ∣ ∣ f ( x ) = 0 } f x 0 f ( x 0 ) = 0 f ( x 0 ) > 0 δ ε x ∈ ( x 0 − δ , x 0 + δ ) f ( x ) ⩾ ε φ ( x ) φ ( x ) = { ε , 0 , x ∈ ( x 0 − δ , x 0 + δ ) , x ∈ / ( x 0 − δ , x 0 + δ ) . f : [ a , b ] → R ⩾ 0 f ⩾ φ ∫ a b f ⩾ ∫ a b φ ⩾ ε δ
反过来, 我们假设 { x ∈ [ a , b ] ∣ ∣ f ( x ) = 0 } f ⩾ 0 φ ( x ) ⩾ 0 φ ( x ) ⩽ f ( x ) ∫ a b ( f − φ ) ⩽ ε
由于
0 ⩽ φ ( x ) ⩽ f ( x ) , 所以
{ x ∈ [ a , b ] ∣ ∣ φ ( x ) = 0 } ⊂ { x ∈ [ a , b ] ∣ ∣ f ( x ) = 0 } , 从而是零测集. 由于
φ 是阶梯函数, 所以
{ x ∈ [ a , b ] ∣ ∣ φ ( x ) = 0 } 是有限集合, 所以
∫ a b φ = 0 . 根据
φ 和
f 之间的关系, 我们有
∫ a b f = ∫ a b ( f − φ ) + ∫ a b φ ⩽ ε + 0. 令
ε → 0 , 我们就证明了
∫ a b f = 0 .
另外一个推论讲的是在一个零测集上改变一个函数的值不会改变这个函数的积分:
f , g ∈ R ( [ a , b ] ) { x ∈ [ a , b ] ∣ ∣ f ( x ) = g ( x ) } ∫ a b f = ∫ a b g
证明. 根据线性, 我们只需要证明, 如果
{ x ∈ [ a , b ] ∣ ∣ f ( x ) = 0 } 是零测集, 那么,
∫ a b f = 0 . 为此, 我们可以用上下积分的定义 (它们都等于函数的积分) : 对任意的
x , 存在阶梯函数
φ , 使得
φ ( x ) ⩾ f ( x ) , ∀ x ∈ [ a , b ] ; ε + ∫ a b f ⩾ ∫ a b φ . 根据
f 的性质, 我们知道
{ x ∈ [ a , b ] ∣ ∣ φ ( x ) < 0 } 是零测集. 由于
φ ( x ) 是阶梯函数, 所以
{ x ∈ [ a , b ] ∣ ∣ φ ( x ) < 0 } 是零测集只能是有限点集, 从而存在一个分划
σ , 其中
σ = { a 0 < a 1 < ⋯ < a n } , 使得对每个
i ⩾ 1 ,
φ ∣ ∣ ( a i − 1 , a i ) 是非负的常数. 特别地, 我们有
∫ a b φ ⩾ 0 ⇒ ∫ a b f ⩾ − ε . 令
ε → 0 , 我们就得到
∫ a b f ⩾ 0 ; 同理, 我们有
∫ a b f ⩽ 0 . 这就证明了命题.
我们现在离开 Lebesgue, 再回到 Newton-Leibniz 公式的场合. 利用这个公式, 我们可以给出积分余项的 Taylor 展开公式:
考虑区间 I = [ a , b ] m + 1 f ∈ C m + 1 ( I ) m ∈ Z ⩾ 0 f ( b ) = k = 0 ∑ m k ! ( b − a ) k f ( k ) ( a ) + ∫ a b m ! ( b − x ) m f ( m + 1 ) ( x ) d x .
证明. 对
m = 0 , 这就是 Newton-Leibniz 公式; 对于一般的
m , 我们进行归纳: 假设命题对
m 是成立的, 即
f ( b ) = k = 0 ∑ m k ! ( b − a ) k f ( k ) ( a ) + ∫ a b m ! ( b − x ) m f ( m + 1 ) ( x ) d x , 所以, 利用 Newton-Leibniz 公式, 我们有
f ( b ) = k = 0 ∑ m k ! ( b − a ) k f ( k ) ( a ) + ∫ a b m ! ( b − x ) m f ( m + 1 ) ( x ) d x = k = 0 ∑ m k ! ( b − a ) k f ( k ) ( a ) + ∫ a b m ! ( b − x ) m ( f ( m + 1 ) ( a ) + ∫ a x f ( m + 2 ) ( y ) d y ) d x = k = 0 ∑ m + 1 k ! ( b − a ) k f ( k ) ( a ) + ∫ a b m ! ( b − x ) m ( ∫ a x f ( m + 2 ) ( y ) d y ) d x . 我们对最后一项用分部积分公式 (注意到边界项是零) :
f ( b ) = k = 0 ∑ m + 1 k ! ( b − a ) k f ( k ) ( a ) − ∫ a b ( ( m + 1 )! ( b − x ) m + 1 ) ′ ( ∫ a x f ( m + 2 ) ( y ) d y ) d x = k = 0 ∑ m + 1 k ! ( b − a ) k f ( k ) ( a ) + ∫ a b ( m + 1 )! ( b − x ) m + 1 ( ∫ a x f ( m + 2 ) ( y ) d y ) ′ d x 由于
f ( m + 2 ) ( x ) 是连续函数, 所以
∫ a x f ( m + 2 ) ( y ) d y 是
f ( m + 2 ) 的原函数, 从而,
( ∫ a x f ( m + 2 ) ( y ) d y ) ′ = f ( m + 2 ) ( x ) , 这就完成了归纳证明.
反常积分的概念 如果一个函数不是定义在一个有界闭区间上, 我们也可以定义积分, 这就是所谓的反常积分. 给定函数 f : [ a , b ) → R b + ∞ b − ∈ [ a , b ) f [ a , b − ] b − < b b − → b lim ∫ a b − f ( x ) d x f [ a , b ) (反常) 可积 并记∫ a b f ( x ) d x = b − → b lim ∫ a b − f ( x ) d x . f [ a , b ) b < ∞ ( a , b ]
在开区间 ( a , b ) a b c ∈ ( a , b ) f ( a , c ] [ c , b ) f ( a , b ) 反常可积 .
根据极限的线性, 我们知道在一个区间 I R
我们对定义用如下的几个例子加以解释:
1)
考虑函数 f ( x ) = sin x [ 0 , ∞ ) x n = 2 nπ n → ∞ lim ∫ 0 x n f ( x ) d x = n → ∞ lim 0 = 0. y n = 2 nπ + 2 π n → ∞ lim ∫ 0 y n f ( x ) d x = n → ∞ lim 1 = 1. b − → ∞ lim ∫ 0 b − f ( x ) d x
2)
考虑函数 f ( x ) = sin x ( − ∞ , ∞ ) R → ∞ lim ∫ − R R f ( x ) d x = R → ∞ lim 0 = 0. ( a , b ) ε → 0 + lim ∫ a + ε b − ε f ( x ) d x
我们来研究几个最为经典的例子, 它们展现了函数衰减/增长的速度对 (反常) 积分收敛性的影响 . 大家应该熟记这些计算和结论:
1)
∫ 1 ∞ x α α
当 α = − 1 M > 1 ∫ 1 M x α = α + 1 1 ( M α + 1 − 1 ) . M → ∞ α < − 1 α = − 1
2)
∫ 0 1 x α α ( 0 , 1 ]
当 α = − 1 ε > 0 ∫ ε 1 x α = α + 1 1 ( 1 − ε α + 1 ) . ε → 0 α > − 1 α = − 1
3)
∫ 2 ∞ x log x 1 d x
对任意的 M > 2 ∫ 2 M x log x 1 d x = ∫ 2 M log x 1 d log x = log log M − log log 2. M → ∞
4)
∫ 100 ∞ x log x log log x 1 M > 100 ∫ 100 M x log x log log x 1 d x = ∫ 100 M log log x 1 d log log x = log log log M − log log log ( 100 ) . M → ∞
5)
∫ 2 ∞ x log α ( x ) 1 α > 1
对任意的 M > 2 ∫ 2 M x log α ( x ) 1 d x = ∫ 2 M log α ( x ) 1 d log x = − α + 1 1 ( ( log M ) α − 1 1 − ( log 2 ) α − 1 1 ) . M → ∞ ( α − 1 ) ( l o g 2 ) α − 1 1
6)
在假设函数 f [ 0 , ∞ ) x → ∞ f → 0
比如说, 我们构造如下的函数: 对任意的 n ∈ Z ⩾ 1 f ( x ) = n , x ∈ [ n − n 3 1 , n ] . f ( x ) ≡ 0 ∫ 0 ∞ f = n = 1 ∑ ∞ n 2 1 x → ∞ lim f ( x ) = 0
关于不定积分, 我们有如下的收敛判别法 (不令人惊讶) :
f F I f : I → R F : I → R J ⊂ I f F J x ∈ I ∣ ∣ f ( x ) ∣ ∣ ⩽ F ( x ) . F I f I
面积法 作为积分的基本应用, 我们用所谓的面积方法来研究级数的大小. 我们大多假设 f ( x ) f [ 1 , n ] f = k = 1 ∑ n − 1 f ( k ) 1 [ k , k + 1 ] ( x ) , f = k = 1 ∑ n − 1 f ( k + 1 ) 1 [ k , k + 1 ] ( x ) . f ⩽ f ⩽ f ∫ 1 n f ⩽ ∫ 1 n f ⩽ ∫ 1 n f . k = 1 ∑ n − 1 f ( k ) ⩽ ∫ 1 n f , k = 2 ∑ n f ( k ) ⩾ ∫ 1 n f . ∫ 1 n k = 1 ∑ ∞ f ( k )
1)
1 ⩽ n ⩽ N ∑ n α = α + 1 N α + 1 − 1 + O ( N α ) α > 0 M > 0 ∣ ∣ N α ∑ 1 ⩽ n ⩽ N n α − α + 1 N α + 1 − 1 ∣ ∣ ⩽ M . f ( x ) = x α 1 ⩽ n ⩽ N ∑ n α 1 ⩽ n ⩽ N ∑ n α ⩽ ∫ 1 N + 1 x α d x = α + 1 ( N + 1 ) α + 1 − 1 . 1 ⩽ n ⩽ N ∑ n α − α + 1 N α + 1 − 1 ⩽ α + 1 ( N + 1 ) α + 1 − N α + 1 . ( N + 1 ) α + 1 − N α + 1 ⩽ C N α C 1 + 2 ⩽ n ⩽ N ∑ n α ⩾ 1 + ∫ 1 N x α d x = 1 + α + 1 N α + 1 − 1 . 1 ⩽ n ⩽ N ∑ n α − α + 1 N α + 1 − 1 ⩽ 1 = O ( N α ) .
2)
关于 k = 1 ∑ n log k
利用函数 f ( x ) = log x k = 1 ∑ n log k ⩾ ∫ 1 n log x = n log n − n + 1. k = 1 ∑ n log k ⩽ ∫ 2 n + 1 log x = ( n + 1 ) log ( n + 1 ) − n + 1 − 2 log 2. ( n + 1 ) log ( n + 1 ) − n + 1 − log 4 ⩽ n log n − n + 1 + log n ( 1 + n 1 ) n + 1 ⩽ 4 n n n log n − n + 1 ⩽ k = 1 ∑ n log k ⩽ n log n − n + 1 + log n . e ⩽ n n e n n ! ⩽ e n .
3)
Euler 常数 γ
定义数列 a n = 1 + 2 1 + 3 1 + ⋯ + n 1 − log n γ = n → ∞ lim ( 1 + 2 1 + 3 1 + ⋯ + n 1 − log n ) . x − 1 1 + 2 1 + 3 1 + ⋯ + n 1 ⩾ ∫ 1 n + 1 x d x = log ( n + 1 ) . 1 + 2 1 + 3 1 + ⋯ + n 1 ⩽ 1 + ∫ 1 n x d x = log ( n ) + 1. 1 + 2 1 + 3 1 + ⋯ + n 1 log ( n ) log ( 1 + n 1 ) ⩽ 1 + 2 1 + 3 1 + ⋯ + n 1 − log n ⩽ 1
然而, 这不足以说明 γ a n a n − log ( 1 + n 1 ) = k = 1 ∑ n ( k 1 − ∫ k k + 1 x d x ) = k = 1 ∑ n ∫ k k + 1 ( k 1 − x 1 ) d x . { a n } n ⩾ 1
我们将在作业题中证明a n − γ = O ( n 1 ) .
根据这个计算, 我们还知道1 − 2 1 + 3 1 − 4 1 + ⋯ + ( − 1 ) n − 1 n 1 + ⋯ = log 2.
人们猜想 γ
log 2 log 2 log 2
Wallis 积分与 Stirling 公式: 三角函数积分的一个应用 历史上, Wallis 研究过如下的定积分I n = ∫ 0 2 π sin n x d x . I 0 = 2 π I 1 = 1 sin x ⩽ 1 { I n } n ⩾ 1 { I n } n ⩾ 1 I n + 2 − I n = ∫ 0 2 π sin n x ( − cos 2 x ) d x = − n + 1 1 ∫ 0 2 π cos x d ( sin n + 1 x ) = − n + 1 sin n + 1 ( x ) cos x ∣ ∣ 0 2 π − n + 1 1 I n + 2 ∫ 0 2 π sin n + 2 x d x . I n + 2 = n + 2 n + 1 I n . I 2 p = 2 2 p ( p ! ) 2 ( 2 p )! 2 π , I 2 p + 1 = ( 2 p + 1 )! 2 2 p ( p ! ) 2 . { I n } n ⩾ 1 n + 2 n + 1 = I n I n + 2 ⩽ 1. n → ∞ lim I n I n + 1 = 1 I 2 p I 2 p + 1 = 2 ( 2 p + 1 ) π { x n } n ⩾ 1 x n = π 2 n I n . x n x n + 2 = n ( n + 2 ) n + 1 ⩾ 1 x 2 p x 2 p + 1 = 2 p + 1 2 p , n → ∞ lim x n = 1 I n ∼ 2 n π , 即 n → ∞ lim 2 n π I n = 1. Wallis 积分的渐进公式 .
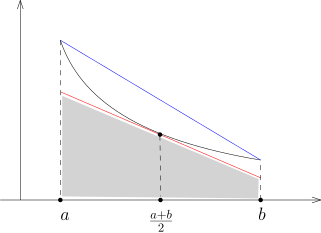
我们现在用 Wallis 积分的计算来推导 Stirling 公式: 考虑数列 { a n } n ⩾ 1 a n = n n + 2 1 e n n ! . n → ∞ lim a n = 2 π log a n + 1 a n = log ( e 1 ( 1 + n 1 ) n + 2 1 ) = ( n + 2 1 ) log ( 1 + n 1 ) − 1. log ( a n + 1 a n ) > 0 x 1 [ a , b ] Γ Γ 2 a + b Γ a b
通过观察面积, 我们知道2 1 ( a 1 + b 1 ) ( b − a ) > ∫ a b x 1 > 2 a + b 1 ( b − a ) . b = n + 1 a = n log a n + 1 a n > 0 { a n } n ⩾ 1 2 ( 2 p + 1 ) I 2 p + 1 = 2 ( 2 p + 1 ) ( 2 p + 1 )! 2 2 p ( p ! ) 2 → π . π = n → ∞ lim ( 2 n )! n ( n ! ) 2 2 2 n = n → ∞ lim a 2 n 2 a n 2 . a n n → ∞ lim a n = n → ∞ lim n n + 2 1 e n n ! = 2 π . n ! ∼ 2 πn ( e n ) n .