10.2. 未知参数的点估计

系数 ${\beta }_0$ 与 ${\beta }_1$ 的点估计

最小二乘估计 (least squares estimation, LSE) 是对线性回归模型 (10.1.1) 中的未知参数 ${\beta }_0,{\beta }_1$ 进行点估计的经典方法. 在最小二乘估计中, 我们考虑如下最优化问题: $$\underset{{\beta }_0,{\beta }_1}{\min }\frac{1}{2}\sum _{i=1}^n{\left(Y_i-{\beta }_0-{\beta }_1{x}_i\right)}^2,$$(10.2.1)在求解 (10.2.1) 时我们把各个 $Y_i$ 看作定值, 则求得的最优解可看作 $Y_1,\dots ,Y_n$ 的函数. 我们将 (10.2.1) 的最优解记为 ${\hat{\beta }}_0$ 与 ${\hat{\beta }}_1$, 它们就是 ${\beta }_0$ 与 ${\beta }_1$ 的最小二乘点估计量. 我们先介绍如何求解最优化问题 (10.2.1), 再对 (10.2.1) 给出的点估计的合理性进行解释.

首先注意到, 最优化问题 (10.2.1) 中对 ${\beta }_0$ 与 ${\beta }_1$ 的取值未做出其它约束, 故可以考虑对目标函数$$S({\beta }_0,{\beta }_1)=\frac{1}{2}\sum _{i=1}^n{\left(Y_i-{\beta }_0-{\beta }_1{x}_i\right)}^2$$求偏导得到驻点, 再验证驻点是否是最小值点. $S({\beta }_0,{\beta }_1)$ 的偏导数由$$\begin{array}{rl}\frac{\partial S({\beta }_0,{\beta }_1)}{\partial {\beta }_0}=& -\sum _{i=1}^n\left(Y_i-{\beta }_0-{\beta }_1{x}_i\right),\\ \frac{\partial S({\beta }_0,{\beta }_1)}{\partial {\beta }_1}=& -\sum _{i=1}^n{x}_i\left(Y_i-{\beta }_0-{\beta }_1{x}_i\right)\end{array}$$给出, 而 $S({\beta }_0,{\beta }_1)$ 的海塞矩阵 (Hessian matrix) 则为$$\mathbf{H}({\beta }_0,{\beta }_1)=\left[\begin{array}{cc}\frac{{\partial }^{2}S({\beta }_0,{\beta }_1)}{\partial {\beta }_0^2}& \frac{{\partial }^{2}S({\beta }_0,{\beta }_1)}{\partial {\beta }_0\partial {\beta }_1}\\ \frac{{\partial }^{2}S({\beta }_0,{\beta }_1)}{\partial {\beta }_1\partial {\beta }_0}& \frac{{\partial }^{2}S({\beta }_0,{\beta }_1)}{\partial {\beta }_1^2}\end{array}\right]=\left[\begin{array}{cc}n& n\overline{x}\\ n\overline{x}& {\sum }_{i=1}^n{x}_i^2\end{array}\right]$$而由于 $x_1,\dots ,x_n$ 不都等于同一个值, 故$$\det \mathbf{H}({\beta }_0,{\beta }_1)=n\sum _{i=1}^n{x}_i^2-n^2{\overline{x}}^2=n\sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2>0,$$再注意到 $\mathbf{H}({\beta }_0,{\beta }_1)$ 的两个对角元均为正数, 可得 $\mathbf{H}({\beta }_0,{\beta }_1)$ 为正定矩阵, 因此 $S({\beta }_0,{\beta }_1)$ 是一个强凸的可微函数, 由多元微积分知识可知, $S({\beta }_0,{\beta }_1)$ 仅存在唯一一个驻点, 且该驻点就是它的最小值点. 由此可得最优化问题 (10.2.1) 的最优解满足方程组$$\begin{array}{rl}n{\hat{\beta }}_0+\left(\sum _{i=1}^n{x}_i\right){\hat{\beta }}_1& =\sum _{i=1}^n{Y}_i,\\ \left(\sum _{i=1}^n{x}_i\right){\hat{\beta }}_0+\left(\sum _{i=1}^n{x}_i^2\right){\hat{\beta }}_1& =\sum _{i=1}^n{x}_i{Y}_i,\end{array}$$(10.2.2)该方程组也被称为 normal equations ¹. 解 normal equations 可得$$\begin{array}{rl}{\hat{\beta }}_0& =\overline{Y}-{\hat{\beta }}_1\overline{x},\\ {\hat{\beta }}_1& =\frac{{\sum }_{i=1}^n{x}_i{Y}_i-n\overline{x}\cdot \overline{Y}}{{\sum }_{i=1}^n{x}_i^2-n{\overline{x}}^2}=\frac{{\sum }_{i=1}^n\left(x_i-\overline{x}\right)Y_i}{{\sum }_{i=1}^n{\left(x_i-\overline{x}\right)}^2},\end{array}$$(10.2.3)其中我们记$$\overline{x}=\frac{1}{n}\sum _{i=1}^n{x}_i,\overline{Y}=\frac{1}{n}\sum _{i=1}^n{Y}_i.$$式 (10.2.3) 给出的 ${\hat{\beta }}_0$ 与 ${\hat{\beta }}_1$ 即为 ${\beta }_0$ 与 ${\beta }_1$ 的最小二乘估计量. 习惯上, 我们还会引入如下记号: $$\begin{array}{rl}{S}_{xx}=& \sum _{i=1}^n(x_i-\overline{x}{)}^2,\\ S_{xY}=& \sum _{i=1}^n\left(x_i-\overline{x}\right)Y_i=\sum _{i=1}^n\left(x_i-\overline{x}\right)(Y_i-\overline{Y}),\end{array}$$(10.2.4)则 ${\hat{\beta }}_1$ 可表示为$${\hat{\beta }}_1=\frac{S_{xY}}{S_{xx}}.$$值得注意的是, ${\hat{\beta }}_1$ 与 ${\hat{\beta }}_0$ 均可看 $Y_1,\dots ,Y_n$ 的线性函数. 在得到回归系数的点估计值以后, 我们可以进一步对回归函数在任意 $x$ 处的取值进行点估计: $$\hat{\mu }(x)={\hat{\beta }}_0+{\hat{\beta }}_{1}x=\overline{Y}+{\hat{\beta }}_1(x-\overline{x}).$$特别地, 我们记$${\hat{Y}}_i=\hat{\mu }(x_i)={\hat{\beta }}_0+{\hat{\beta }}_1{x}_i,i=1,\dots ,n.$$此外, 我们将$$e_i=Y_i-{\hat{Y}}_i=Y_i-({\hat{\beta }}_0+{\hat{\beta }}_1{x}_i)$$称为第 $i$ 个残差 (residual).

接下来, 我们对最小二乘估计的合理性进行解释.

最小二乘估计作为最大似然估计. 在一开始的线性回归模型 (10.1.1) 中, 我们并未指定随机误差 $\epsilon$ 的分布具有怎样的形式, 而只是限定其期望为 $0$ 且方差有限. 而在许多场合下, 为了方便用概率论工具对最小二乘估计进行定量研究, 我们会进一步假定 $\epsilon$ 服从正态分布 $\mathcal{N}(0,{\sigma }^2)$, 此时可以证明, 最小二乘估计 ${\hat{\beta }}_0,{\hat{\beta }}_1$ 也是 ${\beta }_0,{\beta }_1$ 的最大似然估计: 注意到 $\epsilon \sim \mathcal{N}(0,{\sigma }^2)$ 时, 有 $Y_i\sim \mathcal{N}({\beta }_0+{\beta }_1{x}_i,{\sigma }^2)$, 故 $(Y_1,\dots ,Y_n)$ 的联合概率密度函数为$$f(\mathbf{y};{\beta }_0,{\beta }_1,{\sigma }^2,\mathbf{x})=\prod _{i=1}^n\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{(y_i-{\beta }_0-{\beta }_1{x}_i{)}^2}{2{\sigma }^2}\right),$$其中记 $\mathbf{x}=(x_1,\dots ,x_n)$, $\mathbf{y}=(y_1,\dots ,y_n)$. 而将 $f(\mathbf{y};{\beta }_0,{\beta }_1,{\sigma }^2,\mathbf{x})$ 当中的 $\mathbf{x}$ 与 $\mathbf{y}$ 固定, 并把未知参数 ${\beta }_0,{\beta }_1,{\sigma }^2$ 作为自变量, 即可得到似然函数 $L({\beta }_0,{\beta }_1,{\sigma }^2;\mathbf{x},\mathbf{y})$. 相应的对数似然函数为$$\ln L({\beta }_0,{\beta }_1,{\sigma }^2;\mathbf{x},\mathbf{y})=-\frac{1}{2{\sigma }^2}\sum _{i=1}^n{\left(y_i-{\beta }_0-{\beta }_1{x}_i\right)}^2-\frac{n}{2}\ln (2\pi {\sigma }^2),$$(10.2.5)而关于 ${\beta }_0$ 与 ${\beta }_1$ 的对数似然方程则为$$\begin{array}{rl}0& =\frac{\partial \ln L({\beta }_0,{\beta }_1,{\sigma }^2;\mathbf{x},\mathbf{y})}{\partial {\beta }_0}=\frac{1}{{\sigma }^2}\sum _{i=1}^n(y_i-{\beta }_0-{\beta }_1{x}_i),\\ 0& =\frac{\partial \ln L({\beta }_0,{\beta }_1,{\sigma }^2;\mathbf{x},\mathbf{y})}{\partial {\beta }_1}=\frac{1}{{\sigma }^2}\sum _{i=1}^n{x}_i(y_i-{\beta }_0-{\beta }_1{x}_i).\end{array}$$立刻可看出上述方程组与 normal equations (10.2.2) 具有相同的形式. 由此可得如下结论: 当随机误差 $\epsilon$ 服从正态分布 $\mathcal{N}(0,{\sigma }^2)$ 时, ${\beta }_0$ 与 ${\beta }_1$ 的最大似然估计量就是最小二乘估计量.

(${}^{\star }$) 最小二乘估计作为最佳无偏线性估计. 我们还可以从最佳无偏线性估计的角度解释最小二乘估计的合理性. 设 $(x_1,Y_1),\dots ,(x_n,Y_n)$ 为一组样本, 考虑 ${\beta }_0$ 与 ${\beta }_1$ 的关于 $Y_1,\dots ,Y_n$ 具有线性形式的点估计量: $${\hat{\beta }}_1=\sum _{i=1}^n{a}_i{Y}_i,{\hat{\beta }}_0=\sum _{i=1}^n{b}_i{Y}_i,$$其中 $a_1,\dots ,a_n$ 与 $b_1,\dots ,b_n$ 为待定系数, 且要求它们具有无偏性. 我们希望在线性与无偏性的约束下, 找到使得均方误差$$\begin{array}{rl}{\mathrm{MSE}}_{{\beta }_1}({\hat{\beta }}_1)=& \mathbb{E}\left[({\hat{\beta }}_1-{\beta }_1{)}^2\right]\text{与}{\mathrm{MSE}}_{{\beta }_0}({\hat{\beta }}_0)=\mathbb{E}\left[({\hat{\beta }}_0-{\beta }_0{)}^2\right]\end{array}$$对任意的 ${\beta }_0,{\beta }_1$ 与 ${\sigma }^2>0$ 均能取到最小值的系数 $a_1,\dots ,a_n$ 与 $b_1,\dots ,b_n$. 为了后面推导的方便, 我们罗列如下事实:

1.	$Y_1,\dots ,Y_n$ 相互独立.
2.	$\mathbb{E}[Y_i]={\beta }_0+{\beta }_1{x}_i$, $\mathrm{Var}(Y_i)={\sigma }^2$.

首先考虑 ${\beta }_1$ 的最佳无偏线性估计. ${\hat{\beta }}_1={\sum }_{i=1}^n{a}_i{Y}_i$ 的无偏性要求$${\beta }_1=\mathbb{E}\left[\sum _{i=1}^n{a}_i{Y}_i\right]={\beta }_0\cdot \sum _{i=1}^n{a}_i+{\beta }_1\cdot \sum _{i=1}^n{a}_i{x}_i,\forall {\beta }_0,{\beta }_1$$由 ${\beta }_0$ 与 ${\beta }_1$ 的任意性, 可得到$$\sum _{i=1}^n{a}_i=0,\sum _{i=1}^n{a}_i{x}_i=1.$$接下来我们将均方误差 ${\mathrm{MSE}}_{{\beta }_1}({\hat{\beta }}_1)$ 进行展开, 并注意到 ${\hat{\beta }}_1$ 的无偏性, 可得$$\begin{array}{rl}{\mathrm{MSE}}_{{\beta }_1}({\hat{\beta }}_1)=& \mathrm{Var}({\hat{\beta }}_1)=\mathrm{Var}\left(\sum _{i=1}^n{a}_i{Y}_i\right)\\ =& \sum _{i=1}^n{a}_i^2\mathrm{Var}(Y_i)={\sigma }^2\sum _{i=1}^n{a}_i^2.\end{array}$$因此 ${\beta }_1$ 的最佳线性无偏估计的系数 $a_1,\dots ,a_n$ 为如下带约束最优化问题的解: $$\begin{array}{r}\underset{a_1,\dots ,a_n}{\min }\frac{1}{2}\sum _{i=1}^n{a}_i^2\text{s.t.}\sum _{i=1}^n{a}_i=0,\sum _{i=1}^n{a}_i{x}_i=1.\end{array}$$上述问题是一个典型的凸优化问题, 可以用拉格朗日乘子法求出最优解: 该问题的拉格朗日函数为$$\mathcal{L}(a_1,\dots ,a_n,\mu ,\lambda )=\frac{1}{2}\sum _{i=1}^n{a}_i^2+\mu \sum _{i=1}^n{a}_i+\lambda \left(\sum _{i=1}^n{a}_i{x}_i-1\right).$$故最优性条件为$$\begin{array}{rl}0=& \frac{\partial \mathcal{L}(a_1,\dots ,a_n,\mu ,\lambda )}{\partial a_i}=a_i+\mu +\lambda x_i,\\ 0=& \sum _{i=1}^n{a}_i,0=\sum _{i=1}^n{a}_i{x}_i-1.\end{array}$$上述方程组的解为$$a_i=\frac{x_i-\overline{x}}{{\sum }_j{x}_j^2-n{\overline{x}}^2},\mu =\frac{\overline{x}}{{\sum }_j{x}_j^2-n{\overline{x}}^2},\lambda =-\frac{1}{{\sum }_j{x}_j^2-n{\overline{x}}^2}.$$不难发现由上述系数 $a_1,\dots ,a_n$ 给出的线性估计量就是 ${\beta }_1$ 的最小二乘估计量. 同理可证明 ${\beta }_0$ 的最佳线性估计量就是最小二乘估计量, 相关的计算与验证过程交给读者完成.

注 10.2.1. (${}^{\star }$) Normal equations (10.2.2) 有非常直观的几何解释. 设 $(x_1,Y_1),\dots ,(x_n,Y_n)$ 为一组样本, 仍将 $Y_1,\dots ,Y_n$ 看作是定值, 则 $\mathbf{Y}=(Y_1,\dots ,Y_n)$ 可看作 ${\mathbb{R}}^n$ 当中的一个点或一个向量. 记 $\mathbf{x}=(x_1,\dots ,x_n)$, 并用 $1$ 表示分量均为 $1$ 的 $n$ 维向量. 令$$V=\left\{{\beta }_{0}1+{\beta }_1\mathbf{x}\mid {\beta }_0,{\beta }_1\in \mathbb{R}\right\},$$则当 $\mathbf{x}$ 的元素不全相等时, $V$ 构成了 ${\mathbb{R}}^n$ 的一个二维子空间, 而最优化问题 (10.2.1) 则可以等价表示为$$\underset{\mathbf{z}\in V}{\min }\frac{1}{2}\Vert \mathbf{Y}-\mathbf{z}{\Vert }^2,$$其中 $\Vert \cdot \Vert$ 表示欧氏空间 ${\mathbb{R}}^n$ 当中的标准 ${\ell }_2$ 范数. 换句话说, 求解 ${\beta }_0$ 与 ${\beta }_1$ 的最小二乘估计量, 等价于在子空间 $V$ 中找到一个点 (我们将其记为 $\hat{\mathbf{Y}}$) 使得它与 $\mathbf{Y}$ 的距离最小. 由欧氏空间的几何关系, 不难理解这个与 $\mathbf{Y}$ 的距离最小的点 $\hat{\mathbf{Y}}$ 应当使得 $\mathbf{Y}-\hat{\mathbf{Y}}$ 与二维子空间 $V$ 正交 (见图 1). 由于 $\{1,\mathbf{x}\}$ 是子空间 $V$ 的一组基, 可知 $\mathbf{Y}-\hat{\mathbf{Y}}$ 与 $V$ 正交当且仅当 $\mathbf{Y}-\hat{\mathbf{Y}}$ 与 $1$ 和 $\mathbf{x}$ 均正交, 即$$\begin{array}{rl}0=& 1^{\mathsf{T}}\left(\mathbf{Y}-\hat{\mathbf{Y}}\right),\\ 0=& {\mathbf{x}}^{\mathsf{T}}\left(\mathbf{Y}-\hat{\mathbf{Y}}\right).\end{array}$$将 $\hat{\mathbf{Y}}={\hat{\beta }}_{0}1+{\hat{\beta }}_1\mathbf{x}$ 代入并进行化简, 可得$$\begin{array}{rl}0=& \sum _{i=1}^n(Y_i-{\hat{\beta }}_0-{\hat{\beta }}_1{x}_i),\\ 0=& \sum _{i=1}^n{x}_i(Y_i-{\hat{\beta }}_0-{\hat{\beta }}_1{x}_i),\end{array}$$上述方程组正是 normal equations.

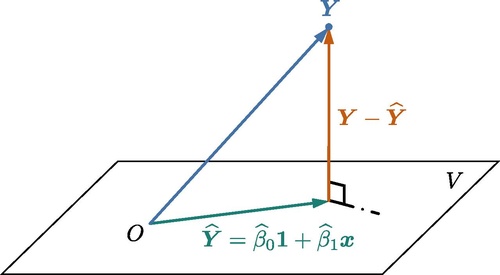图 1. Normal equations 几何直观示意图.

最小二乘估计的偏差与均方误差

本小节中, 我们对 ${\beta }_0$ 与 ${\beta }_1$ 的最小二乘估计的偏差与均方误差进行分析. 设自变量 $x$ 与因变量 $Y$ 之间的确服从 (10.1.1) 给出的线性回归模型. 注意到 $\mathbb{E}[Y_i]={\beta }_0+{\beta }_1{x}_i$, 可得$$\begin{array}{rl}\mathbb{E}\left[{\hat{\beta }}_1\right]=& \mathbb{E}\left[\sum _{i=1}^n\frac{x_i-\overline{x}}{S_{xx}}{Y}_i\right]\\ =& \sum _{i=1}^n\frac{x_i-\overline{x}}{S_{xx}}({\beta }_0+{\beta }_1{x}_i)\\ =& \frac{{\beta }_0}{S_{xx}}\sum _{i=1}^n\frac{x_i-\overline{x}}{S_{xx}}+\frac{{\beta }_1}{S_{xx}}\sum _{i=1}^n\left(x_i^2-x_i\overline{x}\right)\\ =& \frac{{\beta }_1}{S_{xx}}\left(\sum _{i=1}^n{x}_i^2-n{\overline{x}}^2\right)={\beta }_1,\end{array}$$其中利用了 ${\sum }_{i=1}^n(x_i-\overline{x})=0$, 故 ${\hat{\beta }}_1$ 是 ${\beta }_1$ 的一个无偏估计量. ${\hat{\beta }}_1$ 的均方误差也就等于其方差, 为$$\begin{array}{rl}\mathrm{Var}({\hat{\beta }}_1)=& \mathrm{Var}\left(\sum _{i=1}^n\frac{(x_i-\overline{x})Y_i}{S_{xx}}\right)\\ =& \sum _{i=1}^n\frac{(x_i-\overline{x}{)}^2}{S_{xx}^2}\mathrm{Var}(Y_i)\\ =& \frac{{\sum }_{i=1}^n(x_i-\overline{x}{)}^2}{S_{xx}^2}\cdot {\sigma }^2=\frac{{\sigma }^2}{S_{xx}}.\end{array}$$

对于 ${\hat{\beta }}_0$ 则有$$\begin{array}{rl}\mathbb{E}\left[{\hat{\beta }}_0\right]=& \mathbb{E}\left[\overline{Y}-{\hat{\beta }}_1\overline{x}\right]=({\beta }_0+{\beta }_1\overline{x})-{\beta }_1\overline{x}={\beta }_0,\end{array}$$其中利用了 $\mathbb{E}\left[\overline{Y}\right]={\beta }_0+{\beta }_1\overline{x}$ 以及 ${\hat{\beta }}_1$ 的无偏性, 故可得 ${\hat{\beta }}_0$ 是无偏的. 而 ${\hat{\beta }}_0$ 的均方误差也就等于其方差, 为$$\begin{array}{rl}\mathrm{Var}({\hat{\beta }}_0)=& \mathrm{Var}\left(\overline{Y}-{\hat{\beta }}_1\overline{x}\right)\\ =& \mathrm{Var}\left(\sum _{i=1}^n\left(\frac{1}{n}-\frac{x_i-\overline{x}}{S_{xx}}\overline{x}\right)Y_i\right)\\ =& \sum _{i=1}^n{\left(\frac{1}{n}-\frac{x_i-\overline{x}}{S_{xx}}\overline{x}\right)}^2\mathrm{Var}(Y_i)\\ =& {\sigma }^2\sum _{i=1}^n{\left(\frac{1}{n}-\frac{x_i-\overline{x}}{S_{xx}}\overline{x}\right)}^2,\end{array}$$而$$\begin{array}{rl}\sum _{i=1}^n{\left(\frac{1}{n}-\frac{x_i-\overline{x}}{S_{xx}}\overline{x}\right)}^2=& \sum _{i=1}^n\left(\frac{1}{n^2}+\frac{{\overline{x}}^2}{S_{xx}^2}(x_i-\overline{x}{)}^2-\frac{2\overline{x}}{n}(x_i-\overline{x})\right)\\ =& \frac{1}{n}+\frac{{\overline{x}}^2}{S_{xx}}\sum _{i=1}^n(x_i-\overline{x}{)}^2-\frac{2\overline{x}}{n}\sum _{i=1}^n(x_i-\overline{x})\\ =& \frac{1}{n}+\frac{{\overline{x}}^2}{S_{xx}},\end{array}$$故$$\mathrm{Var}({\hat{\beta }}_0)={\sigma }^2\left(\frac{1}{n}+\frac{{\overline{x}}^2}{S_{xx}}\right).$$

最后, 我们对 ${\hat{\beta }}_0$ 与 ${\hat{\beta }}_1$ 的协方差进行计算: $$\begin{array}{rl}\mathrm{Cov}({\hat{\beta }}_0,{\hat{\beta }}_1)=& \mathrm{Cov}(\overline{Y}-{\hat{\beta }}_1\overline{x},{\hat{\beta }}_1)\\ =& \mathrm{Cov}\left(\frac{1}{n}\sum _{i=1}^n{Y}_i,\frac{1}{S_{xx}}\sum _{j=1}^n(x_j-\overline{x})Y_j\right)-\mathrm{Var}({\hat{\beta }}_1)\cdot \overline{x}\\ =& \frac{1}{n{S}_{xx}}\sum _{i,j=1}^n(x_j-\overline{x})\mathrm{Cov}(Y_i,Y_j)-\frac{{\sigma }^2\overline{x}}{S_{xx}}\\ =& \frac{1}{n{S}_{xx}}\sum _{i=1}^n(x_i-\overline{x}){\sigma }^2-\frac{{\sigma }^2\overline{x}}{S_{xx}}\\ =& -\frac{{\sigma }^2\overline{x}}{S_{xx}},\end{array}$$其中倒数第二步是由于 $Y_1,\dots ,Y_n$ 相互独立且 $\mathrm{Var}(Y_i)={\sigma }^2$.

需要指出, 上述推导均不需要假定 ${\epsilon }_1,\dots ,{\epsilon }_n$ 服从正态分布.

方差 ${\sigma }^2$ 的点估计

为了对线性回归模型 (10.1.1) 中随机误差 $\epsilon$ 的方差 ${\sigma }^2$ 进行估计, 我们注意到, 若估计量 ${\hat{\beta }}_0,{\hat{\beta }}_1$ 的值与 ${\beta }_0,{\beta }_1$ 的真值非常接近, 则直观上可以认为$$\begin{array}{rl}{\epsilon }_i=& Y_i-{\beta }_0-{\beta }_1{x}_i\\ \approx & Y_i-{\hat{\beta }}_0-{\hat{\beta }}_1{x}_i=e_i.\end{array}$$注意到随机误差 ${\epsilon }_i$ 不可观测但 $e_i$ 是一个可观测的统计量, 这提示着我们残差 $e_i$ 在对 ${\sigma }^2$ 的估计中将起到关键作用. 不难看出 $e_i$ 的期望为 $0$, 而为了计算 $e_i$ 的方差, 我们注意到$$\begin{array}{rl}{e}_i=& Y_i-(\overline{Y}-{\hat{\beta }}_1\overline{x})-{\hat{\beta }}_1{x}_i=Y_i-\overline{Y}-{\hat{\beta }}_1(x_i-\overline{x})\\ =& Y_i-\frac{1}{n}\sum _{j=1}^n{Y}_j-\frac{x_i-\overline{x}}{S_{xx}}\sum _{j=1}^n(x_j-\overline{x})Y_j\\ =& \left(1-\frac{1}{n}-\frac{(x_i-\overline{x}{)}^2}{S_{xx}}\right)Y_i-\sum _{j\ne i}\left(\frac{1}{n}+\frac{(x_i-\overline{x})(x_j-\overline{x})}{S_{xx}}\right)Y_j,\end{array}$$而由于 $Y_1,\dots ,Y_n$ 之间相互独立, 故$$\begin{array}{rl}\mathrm{Var}(e_i)=& {\left(1-\frac{1}{n}-\frac{(x_i-\overline{x}{)}^2}{S_{xx}}\right)}^2\mathrm{Var}(Y_i)+\sum _{j\ne i}{\left(\frac{1}{n}+\frac{(x_i-\overline{x})(x_j-\overline{x})}{S_{xx}}\right)}^2\mathrm{Var}(Y_j)\\ =& \left[1+{\left(\frac{1}{n}+\frac{(x_i-\overline{x}{)}^2}{S_{xx}}\right)}^2-2\left(\frac{1}{n}+\frac{(x_i-\overline{x}{)}^2}{S_{xx}}\right)\right]{\sigma }^2\\ & +\sum _{j\ne i}{\left(\frac{1}{n}+\frac{(x_i-\overline{x})(x_j-\overline{x})}{S_{xx}}\right)}^2{\sigma }^2\\ =& {\sigma }^2\left[1-2\left(\frac{1}{n}+\frac{(x_i-\overline{x}{)}^2}{S_{xx}}\right)+\sum _{j=1}^n{\left(\frac{1}{n}+\frac{(x_i-\overline{x})(x_j-\overline{x})}{S_{xx}}\right)}^2\right]\\ =& {\sigma }^2\left[1-\frac{2}{n}-\frac{2(x_i-\overline{x}{)}^2}{S_{xx}}+\sum _{j=1}^n\left(\frac{1}{n^2}+\frac{(x_i-\overline{x}{)}^2(x_j-\overline{x}{)}^2}{S_{xx}^2}+\frac{2(x_i-\overline{x})(x_j-\overline{x})}{n{S}_{xx}}\right)\right]\\ =& {\sigma }^2\left[1-\frac{2}{n}-\frac{2(x_i-\overline{x}{)}^2}{S_{xx}}+\frac{1}{n}+\frac{(x_i-\overline{x}{)}^2}{S_{xx}^2}\sum _{j=1}^n(x_j-\overline{x}{)}^2+\frac{2(x_i-\overline{x})}{n{S}_{xx}}\sum _{j=1}^n(x_j-\overline{x})\right]\\ =& {\sigma }^2\left(1-\frac{1}{n}-\frac{(x_i-\overline{x}{)}^2}{S_{xx}}\right),\end{array}$$其中最后一步利用了 ${\sum }_{j=1}^n(x_j-\overline{x}{)}^2=S_{xx}$ 以及 ${\sum }_{j=1}^n(x_j-\overline{x})=0$. 接下来, 我们令$${SS}_{\text{Res}}=\sum _{i=1}^n{\left(Y_i-{\hat{Y}}_i\right)}^2=\sum _{i=1}^n{e}_i^2,$$(10.2.6)并将其称为残差平方和 (residual sum of squares), 则有$$\mathbb{E}\left[{SS}_{\text{Res}}\right]=\sum _{i=1}^n{\sigma }^2\left(1-\frac{1}{n}-\frac{(x_i-\overline{x}{)}^2}{S_{xx}}\right)=(n-2){\sigma }^2.$$由此可得 ${\sigma }^2$ 的一个无偏估计量为$$\widehat{{\sigma }^2}=\frac{1}{n-2}{SS}_{\text{Res}}=\frac{1}{n-2}\sum _{i=1}^n{\left(Y_i-{\hat{\beta }}_0-{\hat{\beta }}_1{x}_i\right)}^2.$$(10.2.7)

残差平方和 ${SS}_{\text{Res}}$ 的一个更加便于计算的表达式为$${SS}_{\text{Res}}={SS}_{\text{T}}-{\hat{\beta }}_1{S}_{xY},\text{其中}{SS}_{\text{T}}=\sum _{i=1}^n{\left(Y_i-\overline{Y}\right)}^2,$$(10.2.8)${SS}_{\text{T}}$ 被称为校正平方和 (corrected sum of squares). 我们将上式的证明留作习题.

需要说明的是, $\widehat{{\sigma }^2}$ 的无偏性并不需要假定 $\epsilon$ 服从正态分布.

脚注

1.	^ 有的地方把 normal equations 译为 “正规方程组”, 但笔者认为这是错译, 这里的 normal 实际上是法向或正交的意思, 合适的译名应当为 “法方程组”. 感兴趣的读者可参阅注 10.2.1 的进一步解释.