9.3. 单个总体下的假设检验

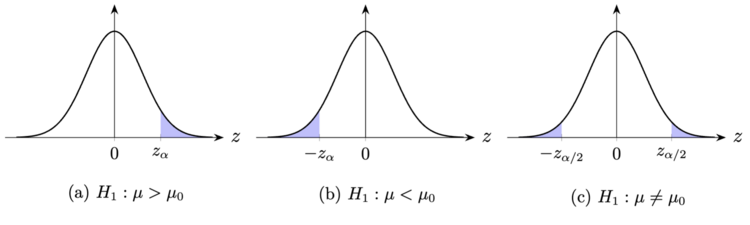
正态总体期望的假设检验

方差 ${\mathbf{\sigma }}^2$ 已知的情形. 设总体服从正态分布 $\mathcal{N}(\mu ,{\sigma }^2)$, 其中方差 ${\sigma }^2>0$ 已知, 我们考虑对未知的期望 $\mu$ 的取值进行假设检验. 相关的结果实际上已经由例 9.1.1 与例 9.1.2 算出来了, 表 1 对其进行了汇总; 图 1 给出了显著性水平为 $\alpha$ 时拒绝域的图示.

原假设 $H_0$	备择假设 $H_1$	检验统计量	拒绝域	$p$ 值
$\mu ={\mu }_0$	$\mu >{\mu }_0$	$Z=\frac{\overline{X}-{\mu }_0}{\sigma /\sqrt{n}}$	$z>z_{\alpha }$	$1-\Phi (z)$
$\mu ={\mu }_0$	$\mu <{\mu }_0$	$Z=\frac{\overline{X}-{\mu }_0}{\sigma /\sqrt{n}}$	$z<-z_{\alpha }$	$\Phi (z)$
$\mu ={\mu }_0$	$\mu \ne {\mu }_0$	$Z=\frac{\overline{X}-{\mu }_0}{\sigma /\sqrt{n}}$	$|z|>z_{\alpha /2}$	$2(1-\Phi (|z|))$

表 1. 方差 ${\sigma }^2$ 已知时, 正态总体期望 $\mu$ 的假设检验方法

图 1. 方差 ${\sigma }^2$ 已知时, 正态总体期望 $\mu$ 的假设检验拒绝域图示, 其中显著性水平为 $\alpha$.

方差 ${\mathbf{\sigma }}^2$ 未知的情形. 设总体服从正态分布 $\mathcal{N}(\mu ,{\sigma }^2)$, 其中期望 $\mu$ 与方差 ${\sigma }^2>0$ 均未知. 我们首先考虑如下假设检验问题: $$H_0:\mu ={\mu }_0,{\sigma }^2>0,H_1:\mu >{\mu }_0,{\sigma }^2>0,$$其中 ${\mu }_0$ 为一给定的实数. 不难看出此时的原假设为复合假设, 而 ${\sigma }^2$ 实际上可以看成一个多余参数 (nuisance parameter). 对于该问题, 我们考虑用$$T=\frac{\overline{X}-{\mu }_0}{\sqrt{S^2/n}}$$(9.3.1)作为单侧检验统计量. 该检验统计量的一个重要特点在于它满足条件 9.2.3: 无论多余参数 ${\sigma }^2$ 的实际取值如何, 在原假设 $H_0$ 下 $T$ 的分布总是不变的, 而且很容看出这个不变的分布就是 $t(n-1)$, 这意味着我们在计算 $p$ 值与临界值时可以直接套用原假设为简单假设时的公式. 由于备择假设中期望相对于原假设的偏离是正向的, 因此 $T$ 的取值越大则意味着相对于 $H_0$ 越显著的偏离. 当显著性水平为 $\alpha$ 时, 由临界值的计算式 ${\mathbb{P}}_{H_0}\left(T>c_{\alpha }\right)=\alpha$ 可求得 $c_{\alpha }=t_{\alpha }(n-1)$, 故拒绝域由$$t=\frac{\overline{x}-{\mu }_0}{\sqrt{s^2/n}}>t_{\alpha }(n-1)$$给出, 其中 $s^2=\frac{1}{n-1}{\sum }_{i=1}^n(x_i-\overline{x}{)}^2$ 为样本观测值 $x_1,\dots ,x_n$ 的样本方差. $p$ 值则由$$\hat{p}={\mathbb{P}}_{{\mu }_0}\left(T\ge t\right)=1-F_{n-1}^t\left(\frac{\overline{x}-{\mu }_0}{\sqrt{s^2/n}}\right)$$给出, 其中 $F_{n-1}^t$ 表示 $t(n-1)$ 的分布函数.

类似地, 若我们希望对期望 $\mu$ 进行双侧检验: $$H_0:\mu ={\mu }_0,{\sigma }^2>0,H_1:\mu \ne {\mu }_0,{\sigma }^2>0,$$则可以将 (9.3.1) 给出的 $T$ 作为双侧检验统计量. 当显著性水平为 $\alpha$ 时, 由临界值计算式 ${\mathbb{P}}_{H_0}\left(T>c_{\alpha }^u\right)={\mathbb{P}}_{H_0}\left(T<c_{\alpha }^l\right)=\alpha /2$ 可得$$c_{\alpha }^u=t_{\alpha /2}(n-1),c_{\alpha }^l=-t_{\alpha /2}(n-1),$$故拒绝域由$$|t|=\frac{|\overline{x}-{\mu }_0|}{\sqrt{s^2/n}}>t_{\alpha /2}(n-1)$$给出. $p$ 值表达式由$$\begin{array}{rl}\hat{p}=& 2\min \{{\mathbb{P}}_{{\mu }_0}(T\ge t),{\mathbb{P}}_{{\mu }_0}(T\le t)\}\\ =& 2\mathbb{P}(T\ge |t|)=2\left(1-F_{n-1}^t\left(\frac{|\overline{x}-{\mu }_0|}{\sqrt{s^2/n}}\right)\right)\end{array}$$给出.

上述利用 $t$ 分布检验统计量进行假设检验的方法被称为 $\mathbf{t}$ 检验法. 表 2 对相关的假设检验方法进行了汇总.

原假设 $H_0$	备择假设 $H_1$	检验统计量	拒绝域	$p$ 值
$\mu ={\mu }_0,{\sigma }^2>0$	$\mu >{\mu }_0,{\sigma }^2>0$	$T=\frac{\overline{X}-{\mu }_0}{\sqrt{S^2/n}}$	$t>t_{\alpha }(n-1)$	$1-F_{n-1}^t(t)$
$\mu ={\mu }_0,{\sigma }^2>0$	$\mu <{\mu }_0,{\sigma }^2>0$	$T=\frac{\overline{X}-{\mu }_0}{\sqrt{S^2/n}}$	$t<-t_{\alpha }(n-1)$	$F_{n-1}^t(t)$
$\mu ={\mu }_0,{\sigma }^2>0$	$\mu \ne {\mu }_0,{\sigma }^2>0$	$T=\frac{\overline{X}-{\mu }_0}{\sqrt{S^2/n}}$	$|t|>t_{\alpha /2}(n-1)$	$2(1-F_{n-1}^t(|t|))$

表 2. 方差 ${\sigma }^2$ 未知时, 正态总体期望 $\mu$ 的假设检验方法

配对样本的 $t$ 检验

配对样本的 $t$ 检验可以看成是单个正态总体期望的 $t$ 检验的特殊情形: 设总体不再是一个随机变量而是一个二维随机向量 $(X,Y)$, 而从该总体中抽样得到的样本是一组配对的随机变量 $(X_1,Y_1),\dots ,(X_n,Y_n)$, 且满足如下条件:

1.	$X-Y$ 服从正态分布 $\mathcal{N}({\mu }_D,{\sigma }_D^2)$, 其中 ${\mu }_D$ 与 ${\sigma }_D^2$ 均未知.
2.	每个 $(X_i,Y_i),i=1,\dots ,n$ 均与 $(X,Y)$ 同分布.
3.	随机向量 $(X_1,Y_1),\dots ,(X_n,Y_n)$ 之间相互独立. 换句话说, 任取 $n$ 个二元实值函数 $f_1,\dots ,f_n:{\mathbb{R}}^2\to \mathbb{R}$, 随机变量 $f_1(X_1,Y_1),\dots ,f_n(X_n,Y_n)$ 均相互独立.

注意上述条件中不要求 $X$ 与 $Y$ 相互独立. 上述配对形式的总体与样本的一个典型的应用场景如下: 为了比较两种方法之间的差异, 我们采取对比实验, 随机选取 $n$ 个对象并在这 $n$ 个对象上分别应用这两种方法, 随后观测两种方法在每个对象上各自给出的效果, 得到成对的样本数据; 此时 $X-Y$ 的期望 ${\mu }_D$ 即可看成是对两种方法效果差别的定量描述.

考虑如下假设检验问题: $$H_0:{\mu }_D={\Delta }_0,H_1:{\mu }_D\ne {\Delta }_0,$$其中 ${\Delta }_0$ 为某个给定的实数 ¹. 由于 $X_i-Y_i$ 均服从正态分布 $\mathcal{N}({\mu }_D,{\sigma }_D^2)$, 其中方差 ${\sigma }_D^2$ 未知, 故可以直接将针对单个正态总体期望的 $t$ 检验法套用过来: 令$$\overline{D}=\frac{1}{n}\sum _{i=1}^n(X_i-Y_i)$$以及$$S_D^2=\frac{1}{n-1}\sum _{i=1}^n(X_i-Y_i-\overline{D}{)}^2,$$则双侧检验统计量应取为$$T=\frac{\overline{D}-{\Delta }_0}{\sqrt{S_D^2/n}}.$$$T$ 在原假设 $H_0$ 下服从自由度为 $n-1$ 的 $t$ 分布, 此后依照上一节给出的 $t$ 检验步骤进行假设检验即可. 对于备择假设为 $H_1:{\mu }_D>{\Delta }_0$ 或 $H_1:{\mu }_D<{\Delta }_0$ 的单侧检验也可按类似方法处理.

正态总体方差的假设检验

设总体服从正态分布 $\mathcal{N}(\mu ,{\sigma }^2)$, 其中期望 $\mu$ 与方差 ${\sigma }^2$ 均未知. 我们先考虑如下假设检验问题: $$H_0:{\sigma }^2={\sigma }_0^2,H_1:{\sigma }^2\ne {\sigma }_0^2,$$其中 ${\sigma }_0^2$ 为一给定的常数. 注意上式中指明 $H_0$ 与 $H_1$ 时, 为了符号上的简单未将未知期望的取值范围 $\mu \in \mathbb{R}$ 明确写出来, $H_0$ 与 $H_1$ 实际上均为复合假设. 对于该假设检验问题, 可以考虑用$${\mathrm{X}}^2=\frac{(n-1)S^2}{{\sigma }_0^2}$$(9.3.2)作为双侧检验统计量. 虽然原假设是复合假设, 但该检验统计量在原假设下总是服从卡方分布 ${\chi }^2(n-1)$ 而与未知期望 $\mu$ 的取值无关, 故条件 9.2.3 成立, 我们可以套用原假设为简单假设时的公式来计算 $p$ 值与临界值. 当显著性水平为 $\alpha$ 时, 由临界值计算式$${\mathbb{P}}_{H_0}\left({\mathrm{X}}^2>c_{\alpha }^l\right)={\mathbb{P}}_{H_0}\left({\mathrm{X}}^2<c_{\alpha }^u\right)=\frac{\alpha }{2},$$可解得$$c_{\alpha }^l={\chi }_{1-\alpha /2}^2(n-1),c_{\alpha }^u={\chi }_{\alpha /2}^2(n-1),$$相应的拒绝域由$$\frac{(n-1)s^2}{{\sigma }_0^2}>{\chi }_{\alpha /2}^2(n-1)\text{或}\frac{(n-1)s^2}{{\sigma }_0^2}<{\chi }_{1-\alpha /2}^2(n-1)$$给出. 而 $p$ 值为$$\begin{array}{rl}\hat{p}=& 2\min \left\{\mathbb{P}\left({\mathrm{X}}^2\ge \frac{(n-1)s^2}{{\sigma }_0^2}\right),\mathbb{P}\left({\mathrm{X}}^2\le \frac{(n-1)s^2}{{\sigma }_0^2}\right)\right\}\\ =& 2\min \left\{1-F_{n-1}^{{\chi }^2}\left(\frac{(n-1)s^2}{{\sigma }_0^2}\right),F_{n-1}^{{\chi }^2}\left(\frac{(n-1)s^2}{{\sigma }_0^2}\right)\right\}\\ =& \{\begin{array}{rlrl}& 2F_{n-1}^{{\chi }^2}\left(\frac{(n-1)s^2}{{\sigma }_0^2}\right),& & \text{若}{F}_{n-1}^{{\chi }^2}\left(\frac{(n-1)s^2}{{\sigma }_0^2}\right)\le \frac{1}{2},\\ & 2-2F_{n-1}^{{\chi }^2}\left(\frac{(n-1)s^2}{{\sigma }_0^2}\right),& & \text{若}{F}_{n-1}^{{\chi }^2}\left(\frac{(n-1)s^2}{{\sigma }_0^2}\right)>\frac{1}{2},\end{array}\end{array}$$其中 $F_{n-1}^{{\chi }^2}$ 表示卡方分布 ${\chi }^2(n-1)$ 的分布函数.

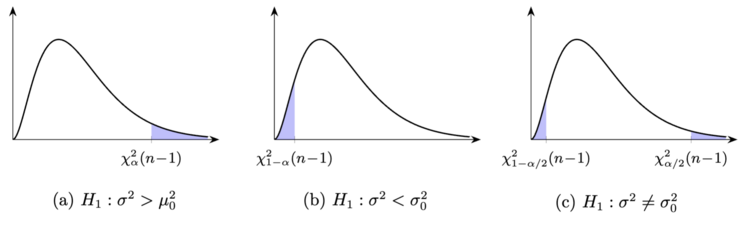
类似地, 若备择假设为 $H_1:{\sigma }^2>{\sigma }_0^2$ 或 $H_1:{\sigma }^2<{\sigma }_0^2$, 则仍可将 (9.3.2) 作为检验统计量, 只不过此时 $H_1$ 相对于 $H_0$ 的偏离是单向的, 故应将 ${\mathrm{X}}^2$ 作为单侧检验量来计算 $p$ 值或拒绝域. 相应的结果总结于表 3 中; 图 2 给出了拒绝域的图示.

$H_0$	$H_1$	检验统计量	拒绝域	$p$ 值
${\sigma }^2={\sigma }_0^2$	${\sigma }^2>{\sigma }_0^2$	$\frac{(n-1)S^2}{{\sigma }_0^2}$	$\frac{(n-1)s^2}{{\sigma }_0^2}>{\chi }_{\alpha }^2(n-1)$	$1-F_{n-1}^{{\chi }^2}\left(\frac{(n-1)s^2}{{\sigma }_0^2}\right)$
${\sigma }^2={\sigma }_0^2$	${\sigma }^2<{\sigma }_0^2$	$\frac{(n-1)S^2}{{\sigma }_0^2}$	$\frac{(n-1)s^2}{{\sigma }_0^2}<{\chi }_{1-\alpha }^2(n-1)$	$F_{n-1}^{{\chi }^2}\left(\frac{(n-1)s^2}{{\sigma }_0^2}\right)$
${\sigma }^2={\sigma }_0^2$	${\sigma }^2\ne {\sigma }_0^2$	$\frac{(n-1)S^2}{{\sigma }_0^2}$	$\begin{array}{rl}& \frac{(n-1)s^2}{{\sigma }_0^2}>{\chi }_{\alpha /2}^2(n-1)\text{ 或}\\ & \frac{(n-1)s^2}{{\sigma }_0^2}<{\chi }_{1-\alpha /2}^2(n-1)\end{array}$	$\begin{array}{rl}2\min \{F_{n-1}^{{\chi }^2}\left(\frac{(n-1)s^2}{{\sigma }_0^2}\right),& \\ 1-F_{n-1}^{{\chi }^2}\left(\frac{(n-1)s^2}{{\sigma }_0^2}\right)\}& \end{array}$

表 3. 期望 $\mu$ 未知时, 正态总体方差 ${\sigma }^2$ 的假设检验方法

图 2. 期望 $\mu$ 未知时, 正态总体方差 ${\sigma }^2$ 的假设检验拒绝域图示, 其中横坐标为 $(n-1)s^2/{\sigma }_0^2$, 显著性水平取为 $\alpha$.

比例的假设检验

设总体 $X$ 服从参数为 $p$ 的伯努利分布, 其中 $p$ 未知; 我们通常将参数 $p$ 解释为某种比例 (可参考第 8.2 节最后一小节的说法). 考虑如下假设检验问题: $$H_0:p=p_0,H_1:p\ne p_0.$$

当样本容量 $n$ 较小时, 我们可以考虑用 $p$ 值法: 以 $K={\sum }_{i=1}^n{X}_i$ 作为双侧检验统计量, 则在原假设 $H_0$ 下, $K$ 服从参数为 $(n,p_0)$ 的二项分布, 从而对于样本观测值 $x_1,\dots ,x_n$, 其 $p$ 值为$$\begin{array}{rl}\hat{p}=& 2\min \left\{{\mathbb{P}}_{p_0}\left(\sum _{i=1}^n{X}_i\ge \sum _{i=1}^n{x}_i\right),{\mathbb{P}}_{p_0}\left(\sum _{i=1}^n{X}_i\le \sum _{i=1}^n{x}_i\right)\right\}\\ =& 2\min \left\{1-\sum _{j=0}^{k-1}\left(\genfrac{}{}{0ex}{}{n}{j}\right)p_0^j(1-p_0{)}^{n-j},\sum _{j=0}^k(\genfrac{}{}{0ex}{}{n}{j})p_0^j(1-p_0{)}^{n-j}\right\}\\ =& 2\min \left\{\sum _{j=k}^n\left(\genfrac{}{}{0ex}{}{n}{j}\right)p_0^j(1-p_0{)}^{n-j},1-\sum _{j=k+1}^n(\genfrac{}{}{0ex}{}{n}{j})p_0^j(1-p_0{)}^{n-j}\right\},\end{array}$$其中我们记$$k=\sum _{i=1}^n{x}_i.$$若需要在 $H_0$ 与 $H_1$ 之间二选一, 则可比较 $p$ 值与事先设定的显著性水平 $\alpha$, 当 $p$ 值小于 $\alpha$ 时拒绝原假设, 否则接受原假设.

注 9.3.1. (${}^{\star }$) 利用分部积分, 可证明 $1\le j\le n-1$ 时, $$n\left(\genfrac{}{}{0ex}{}{n-1}{j-1}\right){\int }_0^p{t}^{j-1}(1-t{)}^{n-j}\mathrm{d}t-n(\genfrac{}{}{0ex}{}{n-1}{j}){\int }_0^p{t}^j(1-t{)}^{n-j-1}\mathrm{d}t=\left(\genfrac{}{}{0ex}{}{n}{j}\right)p^j(1-p{)}^{n-j},$$而$$n{\int }_0^p{t}^{n-1}\mathrm{d}t=\left(\genfrac{}{}{0ex}{}{n}{n}\right)p^n(1-p{)}^0,$$故 $1\le k\le n$ 时, 可得$$\begin{array}{rl}& \sum _{j=k}^n\left(\genfrac{}{}{0ex}{}{n}{j}\right)p^j(1-p{)}^{n-j}\\ =& \sum _{j=k}^{n-1}\left[n\left(\genfrac{}{}{0ex}{}{n-1}{j-1}\right){\int }_0^p{t}^{j-1}(1-t{)}^{n-j}\mathrm{d}t-n(\genfrac{}{}{0ex}{}{n-1}{j}){\int }_0^p{t}^j(1-t{)}^{n-j-1}\mathrm{d}t\right]\\ & +n{\int }_0^p{t}^{n-1}\mathrm{d}t\\ =& n\left(\genfrac{}{}{0ex}{}{n-1}{k-1}\right){\int }_0^p{t}^{k-1}(1-t{)}^{n-k}\mathrm{d}t\\ =& I_p(k,n-k+1),\end{array}$$其中$$I_x(a,b)=\frac{\Gamma (a+b)}{\Gamma (a)\Gamma (b)}{\int }_0^x{t}^{a-1}(1-t{)}^{b-1}\mathrm{d}t$$为不完全 Beta 函数 (incomplete beta function). 由此可将 $p$ 值表达式改写为$$\hat{p}=2\min \{I_{p_0}(k,n-k+1),1-I_{p_0}(k+1,n-k)\},$$从而 $\hat{p}<\alpha$ 给出的拒绝域可等价表示为$$I_{p_0}(k,n-k+1)<\frac{\alpha }{2}\text{或}1-I_{p_0}(k,n-k+1)<\frac{\alpha }{2}.$$我们可以进一步利用 Beta 分布的上分位数或 $F$ 分布的上分位数来表示拒绝域, 感兴趣的读者可参阅 [21] 第 3.8.3 节以及 [22] 第 27.2 节.

当样本容量 $n$ 足够大时, 利用中心极限定理可得$$\begin{array}{rl}{\mathbb{P}}_{p_0}\left(\sum _{i=1}^n{X}_i\ge k\right)=& {\mathbb{P}}_{p_0}\left(\sum _{i=1}^n{X}_i\ge k-\frac{1}{2}\right)\approx 1-\Phi \left(\frac{k-1/2-n{p}_0}{\sqrt{n{p}_0(1-p_0)}}\right),\end{array}$$其中第一步为连续性修正. 同理, $${\mathbb{P}}_{p_0}\left(\sum _{i=1}^n{X}_i\le k\right)\approx \Phi \left(\frac{k+1/2-n{p}_0}{\sqrt{n{p}_0(1-p_0)}}\right)=1-\Phi \left(\frac{-k-1/2+n{p}_0}{\sqrt{n{p}_0(1-p_0)}}\right),$$故$$\hat{p}\approx 2\left(1-\Phi \left(\frac{|k-n{p}_0|-1/2}{\sqrt{n{p}_0(1-p_0)}}\right)\right).$$而当给定显著性水平为 $\alpha$ 时, 相应的拒绝域可近似由$$\frac{|k-n{p}_0|-1/2}{\sqrt{n{p}_0(1-p_0)}}>z_{\alpha /2}$$给出.

对于备择假设为 $H_1:p<p_0$ 或 $H_1:p>p_0$ 的单侧检验问题, 仍可利用上述方法导出相应的 $p$ 值与拒绝域, 我们将具体的推导留给读者完成.

脚注

1.	^ 若取 ${\Delta }_0=0$, 则原假设即意味着被测试的两种方法的平均效果没有差别.