8.1. 区间估计与置信区间

设总体的分布函数为 $F(x;\theta )$, 其中未知参数 $\theta$ 的所有可能取值构成集合 $\Theta$, 且为简单起见, 设 $\Theta$ 是 $\mathbb{R}$ 上的一个区间. 在点估计问题中, 我们通过构造合适的统计量 $\hat{\theta }$, 基于获得的样本值来给出未知参数 $\theta$ 的单个估计值. 然而, 在某些实际问题中, 我们可能不仅需要进行点估计, 还希望基于样本对这个点估计的精度进行某种推断. 例如, 我们可能希望找到一个阈值, 使得点估计值与真实值的距离能够以大概率小于等于该阈值, 那么我们就可以用这个阈值来代表估计的精度. 由于真实的总体未知, 我们也只能基于样本值来给出这个阈值, 故这个阈值也对应于一个统计量. 将以上想法进行整理后, 我们就得到了如下问题: 应当如何构造点估计量 $\hat{\theta }$ 以及一个阈值统计量 $D=D(X_1,\dots ,X_n)$, 使得不等式$${\mathbb{P}}_{\theta }(|\hat{\theta }-\theta |\le D)\ge 1-\alpha$$对任意 $\theta \in \Theta$ 成立, 其中 $\alpha$ 是一个事先定好的足够小的实数. 不难看出上述问题也等价于如何构造统计量 $\underline{\theta }=\underline{\theta }(X_1,\dots ,X_n)$ 与 $\overline{\theta }=\overline{\theta }(X_1,\dots ,X_n)$, 使得$${\mathbb{P}}_{\theta }\left(\right[\underline{\theta },\overline{\theta }]\ni \theta )\ge 1-\alpha ,\forall \theta \in \Theta ,$$(8.1.1)其中 $\alpha$ 是一个事先定好的足够小的实数. 换句话说, 我们希望找到一个依赖于样本的区间 $[\underline{\theta },\overline{\theta }]$, 使得无论总体的真实参数 $\theta$ 是什么, 这个区间能够覆盖住真实参数 $\theta$ 的概率至少为 $1-\alpha$. 我们把这一类问题称为区间估计 (interval estimation) 问题, 而将满足条件 (8.1.1) 的端点为统计量的区间 $[\underline{\theta },\overline{\theta }]$ 称为 $\theta$ 的置信区间 (confidence interval), 并把 $1-\alpha$ 叫作该置信区间的置信水平 (confidence level) ¹. 我们还经常将 $\underline{\theta }$ 与 $\overline{\theta }$ 分别称为置信下限与置信上限 (lower/upper confidence limit).

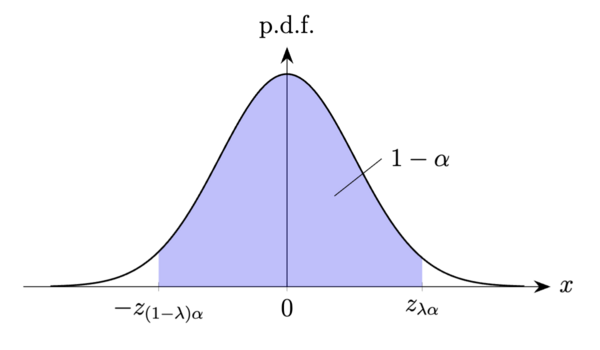
对于置信水平为 $1-\alpha$ 的置信区间 $[\underline{\theta },\overline{\theta }]$, 我们可以认为 $1-\alpha$ 衡量了区间估计的可靠性, 而 $\overline{\theta }-\underline{\theta }$ 则衡量了区间估计的精度. 不难理解可靠性与精度之间是存在一定矛盾的, 一般来说, 在样本容量 $n$ 受限的情形下, 我们不可能把区间估计的可靠性与精度都同时提升到一个很高的水平. 在经典的频率学派区间估计理论中, 我们采取的方案是先给定可靠性的一个下限 (也即确定置信水平), 在保证这个下限的前提下尽量提升区间估计的精度 ². 换句话说, 在针对给定的 $\alpha$ 求解置信区间 $[\underline{\theta },\overline{\theta }]$ 时, 我们会在保证其置信水平至少为 $1-\alpha$ 的前提下, 尽量让该区间的宽度 $\overline{\theta }-\underline{\theta }$ 取得越小越好. 通常, 这将迫使我们让 $[\underline{\theta },\overline{\theta }]\ni \theta$ 的概率尽可能地下探到 $1-\alpha$ (但不得低于 $1-\alpha$); 特别是, 当总体 $X$ 是连续型随机变量时, 我们通常就按要求$$\underset{\theta \in \Theta }{\inf }{\mathbb{P}}_{\theta }\left(\right[\underline{\theta },\overline{\theta }]\ni \theta )=1-\alpha$$来求置信区间.

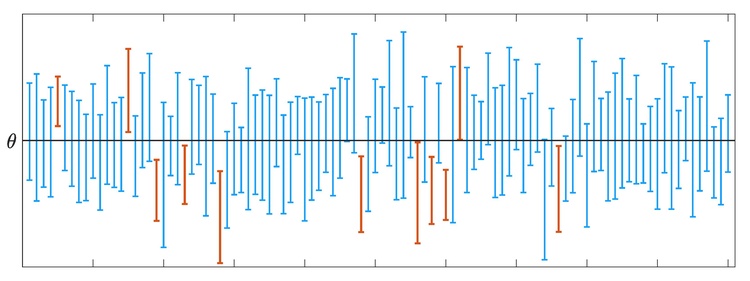
需要注意的是, 式 (8.1.1) 当中出现的参数 $\theta$ 是被作为一个确定性的量处理的, 也就是说, 我们目前是以频率学派的视角来对待区间估计问题的, 而这也要求我们在理解 (8.1.1) 的含义时需要格外小心. 特别是, 我们不能认为式 (8.1.1) 体现了未知参数 $\theta$ 的统计规律 (因为 $\theta$ 是一个确定性的量). 一种解释 (8.1.1) 含义的方式如下: 设总体的参数为某个确定性的 $\theta$, 而我们通过从这个总体中反复地抽样, 按照统计量 $\underline{\theta }$ 与 $\overline{\theta }$ 来大量重复上述置信区间的构造流程 (比方说重复 $M$ 次), 从而获得 $M$ 个置信区间的结果. 由于每次抽样获得的样本值是不同的, 这 $M$ 个区间也互不相同. 则平均而言, 在这大量的区间估计给出的结果中, 把参数真值 $\theta$ 覆盖住的区间所占的比例将至少为 $1-\alpha$; 可参考图 1 给出的图示.

图 1. 固定总体参数 $\theta$, 对某个置信水平为 $90\%$ 的置信区间构造流程重复 100 次的实验结果. 图中每个 “工” 字图形表示一个区间估计的结果, 蓝色表示该区间覆盖住了参数真值, 而红色表示该区间没能覆盖住参数真值. 当重复次数进一步提升并趋于无穷时, 蓝色区间所占比例将趋于 $90\%$.

例 8.1.1 (方差已知时正态总体期望的区间估计). 设总体 $X$ 服从正态分布 $\mathcal{N}(\mu ,{\sigma }^2)$, 其中方差 ${\sigma }^2$ 已知而期望 $\mu$ 未知, $X_1,\dots ,X_n$ 为总体 $X$ 的一组样本, 我们希望对期望 $\mu$ 进行区间估计, 找出其置信水平为 $1-\alpha$ 的一个置信区间.

注意到样本均值 $\overline{X}=\frac{1}{n}{\sum }_{i=1}^n{X}_i$ 服从正态分布 $\mathcal{N}(\mu ,{\sigma }^2/n)$, 因而$$\frac{\overline{X}-\mu }{\sqrt{{\sigma }^2/n}}\sim \mathcal{N}(0,1).$$可以看出随机变量 $(\overline{X}-\mu )/\sqrt{{\sigma }^2/n}$ 的分布已不再依赖于未知参数 $\mu$. 现任取 $\lambda \in \left]0,1\right[$, 依照标准正态分布上分位数的定义以及正态分布的对称性, 可得 (见图 2)$${\mathbb{P}}_{\mu }\left(-z_{(1-\lambda )\alpha }\le \frac{\overline{X}-\mu }{\sqrt{{\sigma }^2/n}}\le z_{\lambda \alpha }\right)=1-\alpha .$$对上式进行变形, 得到$${\mathbb{P}}_{\mu }\left(\left[\overline{X}-z_{\lambda \alpha }\frac{\sigma }{\sqrt{n}},\overline{X}+z_{(1-\lambda )\alpha }\frac{\sigma }{\sqrt{n}}\right]\ni \mu \right)=1-\alpha .$$由此可得, 形如$$\left[\overline{X}-z_{\lambda \alpha }\frac{\sigma }{\sqrt{n}},\overline{X}+z_{(1-\lambda )\alpha }\frac{\sigma }{\sqrt{n}}\right].$$的随机区间均为 $\mu$ 的置信水平为 $1-\alpha$ 的置信区间. 但在所有这些置信区间中, 令 $\lambda =1/2$ 可以使置信区间的宽度达到最小, 因而我们通常就将$$\left[\overline{X}-z_{\alpha /2}\frac{\sigma }{\sqrt{n}},\overline{X}+z_{\alpha /2}\frac{\sigma }{\sqrt{n}}\right]$$(8.1.2)作为 $\mu$ 的置信水平为 $1-\alpha$ 的置信区间.

图 2. 正态总体的方差已知时, 利用枢轴量 $(\overline{X}-\mu )/\sqrt{{\sigma }^2/n}$ 求解期望的置信区间.

注 8.1.2. 例 8.1.1 考虑的是总体服从正态分布的情形. 而若总体不服从正态分布但其方差 ${\sigma }^2$ 已知, 且样本容量 $n$ 足够大, 则由中心极限定理可得 $(\overline{X}-\mu )/\sqrt{{\sigma }^2/n}$ 近似服从标准正态分布, 此时我们可以依照例 8.1.1 的步骤对期望 $\mu$ 的置信区间进行近似求解, 并最终得到其置信水平为 $1-\alpha$ 的置信区间可以近似由式 (8.1.2) 给出.

注 8.1.3. 对于某些场合, 我们可能只是想估计出未知参数 $\theta$ 的一个上界, 并在保证一定可靠性的前提下让这个上界尽可能接近参数的真值. 换句话说, 给定 $\alpha$, 我们只需找到一个尽量小的统计量 $\overline{\theta }$ 使得$${\mathbb{P}}_{\theta }\left(\theta \le \overline{\theta }\right)\ge 1-\alpha$$(8.1.3)即可. 我们将满足 (8.1.3) 的统计量 $\overline{\theta }$ 称作置信水平为 $1-\alpha$ 的单侧置信上界 (one-sided upper confidence bound). 对于单侧置信上界, 其估计精度可以直接由它的大小来衡量, 即单侧置信上界越小则估计精度越高. 同理也可定义单侧置信下界 (one-sided lower confidence bound) 的概念. 此外, 我们也将形如$$\left]-\infty ,\overline{\theta }\right]\text{或}\left[\underline{\theta },+\infty \right[$$的置信区间称作单侧置信区间 (one-sided confidence interval).

以例 8.1.1 考虑的情形为例, 给定置信水平 $1-\alpha$, 则未知参数 $\mu$ 的两个单侧置信区间可以分别取为$$\left]-\infty ,\overline{X}+z_{\alpha }\frac{\sigma }{\sqrt{n}}\right]\text{与}\left[\overline{X}-z_{\alpha }\frac{\sigma }{\sqrt{n}},+\infty \right[$$(注意上式中用到的上分位数为 $z_{\alpha }$ 而非 $z_{\alpha /2}$).

我们可以将例 8.1.1 的区间估计步骤进行推广, 得到求解置信区间的一个较为一般的方法:

1.	构造一个依赖于样本 $X_1,\dots ,X_n$ 与参数值 $\theta$ 的随机变量 $h(X_1,\dots ,X_n;\theta )$, 使得 $h(X_1,\dots ,X_n;\theta )$ 的分布不再与未知参数有关 (换句话说, $h(X_1,\dots ,X_n;\theta )$ 在取不同的 $\theta$ 时所服从的分布都是相同的). 我们将该随机变量 $h(X_1,\dots ,X_n;\theta )$ 称作一个枢轴量 (pivotal quantity). 在例 8.1.1 当中, 枢轴量即为 $(\overline{X}-\mu )/\sqrt{{\sigma }^2/n}$.
2.	找出两个合适的常数 $l$ 与 $u$, 使得$${\mathbb{P}}_{\theta }\left(l\le h(X_1,\dots ,X_n;\theta )\le u\right)\ge 1-\alpha .$$特别是, 若 $h(X_1,\dots ,X_n;\theta )$ 为连续型随机变量, 则找出满足$${\mathbb{P}}_{\theta }\left(l\le h(X_1,\dots ,X_n;\theta )\le u\right)=1-\alpha$$的常数 $l,u$. 在例 8.1.1 当中, 由于枢轴量服从标准正态分布, 故可以取 $l=-z_{(1-\alpha )\lambda },u=z_{\lambda \alpha }$. 而取 $\lambda =1/2$ 可以使得最终构造出来的置信区间宽度最小.
3.	尝试将不等式 $l\le h(X_1,\dots ,X_n;\theta )\le u$ 等价地变形为如下形式: $$\underline{\theta }(X_1,\dots ,X_n)\le \theta \le \overline{\theta }(X_1,\dots ,X_n).$$若这样的等价变形可行, 则可知 $\theta$ 的一个置信水平为 $1-\alpha$ 的置信区间为$$\left[\underline{\theta }(X_1,\dots ,X_n),\overline{\theta }(X_1,\dots ,X_n)\right].$$

我们将上述求解置信区间的方法称作枢轴量法. 需要注意的是, 枢轴量法并非万能, 其中枢轴量的构造对于总体分布的形式较为复杂的情形往往是比较困难的.

注 8.1.4. 若总体的未知参数为 $\theta \in \Theta$ (它可以是标量也可以是多维向量), 而我们想对 $\eta =g(\theta )$ 进行区间估计, 其中 $g:\Theta \to \mathbb{R}$ 为一个实值函数, 则此时 $\eta$ 的置信水平为 $1-\alpha$ 的置信区间 $\left[\underline{\eta },\overline{\eta }\right]$ 需满足如下条件: $${\mathbb{P}}_{\theta }\left(\left[\underline{\eta },\overline{\eta }\right]\ni g(\theta )\right)\ge 1-\alpha ,\forall \theta \in \Theta ,$$其中区间端点 $\underline{\eta },\overline{\eta }$ 仍要求为统计量. 此时依然可以考虑用枢轴量法构造置信区间, 不过我们会要求枢轴量的形式为 $h(X_1,\dots ,X_n;g(\theta ))$, 也就是说它只和 $X_1,\dots ,X_n$ 与 $g(\theta )$ 有关; 另一方面, 我们仍然要求 $h(X_1,\dots ,X_n;g(\theta ))$ 的分布与 $\theta$ 无关. 此时通过$${\mathbb{P}}_{\theta }\left(l\le h(X_1,\dots ,X_n;g(\theta ))\le u\right)\ge 1-\alpha$$即可构造 $\eta =g(\theta )$ 的置信区间.

上述情形的一个特例是总体存在多个未知标量参数 $\theta ,{\lambda }_1,\dots ,{\lambda }_k$, 而我们想对其中一个未知标量参数 $\theta$ 进行区间估计. 此时其余的参数 $\mathbf{\lambda }=({\lambda }_1,\dots ,{\lambda }_k)$ 被称为多余参数 (nuisance parameter, 其它中文称谓还包括冗余参数、讨厌参数、干扰参数等). 存在多余参数 $\mathbf{\lambda }$ 时, $\theta$ 的置信水平为 $1-\alpha$ 的置信区间 $\left[\underline{\theta },\overline{\theta }\right]$ 则需满足如下条件: $${\mathbb{P}}_{\theta ,\mathbf{\lambda }}\left(\left[\underline{\theta },\overline{\theta }\right]\ni \theta \right)\ge 1-\alpha ,\forall \theta \in \Theta ,\mathbf{\lambda }\in \Lambda ,$$其中 $\Theta$ 为 $\theta$ 的取值范围, $\Lambda$ 为多余参数 $\mathbf{\lambda }$ 的取值范围. 对于存在多余参数的情形, 若要用枢轴量法求 $\theta$ 的置信区间, 则要求枢轴量 $h(X_1,\dots ,X_n;\theta )$ 只和 $X_1,\dots ,X_n$ 与 $\theta$ 有关而与 $\mathbf{\lambda }$ 无关, 但同时要求 $h(X_1,\dots ,X_n;\theta )$ 的分布与 $\theta$ 和 $\mathbf{\lambda }$ 均无关. 此时由$${\mathbb{P}}_{\theta ,\mathbf{\lambda }}\left(l\le h(X_1,\dots ,X_n;\theta )\le u\right)\ge 1-\alpha$$构造的 $\theta$ 的置信区间则可用于多余参数 $\mathbf{\lambda }$ 未知的情形.

在接下来的几节中, 我们将针对几类常见的区间估计问题, 介绍其置信区间的求解流程. 我们只给出 (双侧) 置信区间的构造流程, 但读者可自行推导相应的单侧置信上界与单侧置信下界.

脚注

1.	^ 注意到若 $1-\alpha$ 是 $[\underline{\theta },\overline{\theta }]$ 的置信水平, 那么任何小于等于 $1-\alpha$ 的正实数也都是 $[\underline{\theta },\overline{\theta }]$ 的置信水平. 有些场合为了表意上的确切, 当给定置信区间而谈论其置信水平时, 我们是指满足 (8.1.1) 的 $1-\alpha$ 当中最大的那个值.
2.	^ 这套区间估计的范式是由统计学家 Jerzy Neyman 首先建立的.