2.6. 伯努利过程

本节中, 我们基于伯努利过程来阐述二项分布、几何分布与泊松分布的来源、意义和联系.

定义 2.6.1. 设 $X_1,X_2,\dots$ 为一列随机变量, $p\in (0,1]$. 我们称随机变量列 $(X_n{)}_{n=1}^{\infty }$ 为一参数为 $p$ 的伯努利过程 (Bernoulli process), 若 $X_1,X_2,\dots$ 相互独立, 且每个 $X_n$ 服从参数为 $p$ 的伯努利分布, 即$$\mathbb{P}(X_n=1)=p,\mathbb{P}(X_n=0)=1-p.$$

给定一伯努利过程 $(X_n{)}_{n=1}^{\infty }$, 我们进一步定义$$N_0=0,N_n=\sum _{k=1}^n{X}_k,n=1,2,3,\dots$$并用递归的方式定义$$\begin{array}{rl}{T}_1& =\min \{n\in {\mathbb{N}}_{+}\mid N_n\ge 1\},\\ T_k& =\min \{n\in {\mathbb{N}}_{+}\mid N_n\ge k\}-\sum _{i=1}^{k-1}{T}_i,k=2,3,4,\dots \end{array}$$可以将伯努利过程 $(X_n{)}_{n=1}^{\infty }$ 及相应的 $(N_n{)}_{n=1}^{\infty }$、$(T_k{)}_{k=1}^{\infty }$ 与独立重复的伯努利试验相关联: 设有某个试验, 其结果只有成功和失败两种, 成功的概率为 $p$, 失败的概率为 $1-p$, 我们把这样的试验被称为伯努利试验. 我们在离散时刻 $n=1,2,3,\dots$ 独立地重复该试验, 每个时刻对应于一次试验, 则事件 $\{X_n=1\}$ 代表第 $n$ 次试验成功, 而 $N_n$ 的值代表了时间段 $\{1,\dots ,n\}$ 内试验的总成功次数, $T_1$ 的值代表了从初始时刻到第 $1$ 次成功之间的等待时间, $k\ge 2$ 时 $T_k$ 的值代表了第 $k-1$ 次成功到第 $k$ 次成功之间的等待时间; 见图 1.

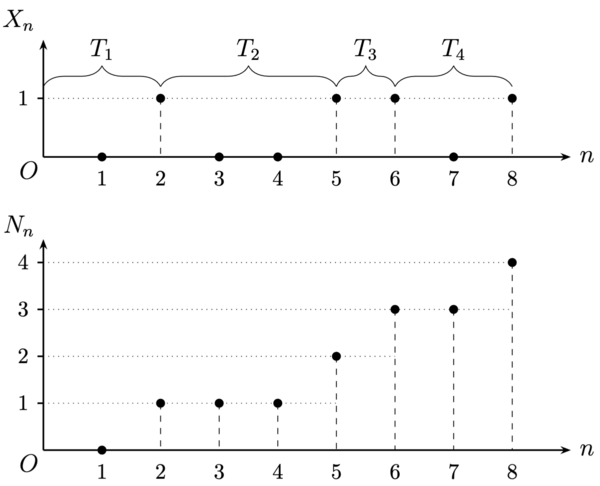图 1. 伯努利过程中 $X_n,N_n$ 与 $T_k$ 的图示.

$N_n$ 的分布. 我们先考察 $N_n$ 的分布. 显然 $N_n$ 为离散型随机变量, 其取值范围为 $\{0,1,\dots ,n\}$. 任取 $k\in \{0,1,\dots ,n\}$, 由基础的组合数学知识可知, 事件 $\{N_n=k\}$ 可看成是 $\left(\genfrac{}{}{0ex}{}{n}{k}\right)$ 个形如$$\{X_1=x_1,\dots ,X_n=x_n\},\text{x1,…,xn当中有k个等于1，其余n−k个等于0}$$的互不相交的事件的并, 而由于 $X_1,X_2,\dots$ 相互独立, 可知每个形如上式的事件的概率为$$\mathbb{P}(X_1=x_1,\dots ,X_n=x_n)=\mathbb{P}(X_1=x_1)\cdots \mathbb{P}(X_n=x_n)=p^k(1-p{)}^{n-k}.$$故 $N_n$ 的分布列为$$p_{N_n}(k)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)p^k(1-p{)}^{n-k},k=0,1,\dots ,n.$$(2.6.1)由此可看出 $N_n$ 服从参数为 $p$ 的二项分布.

上述结果为二项分布期望与方差的计算提供了一种简便方法: 利用期望的线性, 可得$$\mathbb{E}[N_n]=\mathbb{E}\left[\sum _{i=1}^n{X}_i\right]=\sum _{i=1}^n\mathbb{E}[X_i]=np,$$以及$$\mathrm{Var}(N_n)=\mathrm{Var}\left(\sum _{i=1}^n{X}_i\right)=\sum _{i=1}^n\mathrm{Var}(X_i)=np(1-p).$$上式第二步用到了 $X_1,X_2,\dots$ 的独立性. 注意到期望与方差的值仅取决于分布本身, 可得参数为 $(n,p)$ 的二项分布的期望为 $np$, 方差为 $np(1-p)$.

$T_1$ 的分布. 接下来我们考察从初始时刻到第一次成功的等待时间 $T_1$, 它是一个离散型随机变量, 其取值可以是任意正整数. 为求出 $T_1$ 的分布, 任取一正整数 $k$, 由 $T_1$ 的定义可得, $$T_1=k⟺X_1=\cdots =X_{k-1}=0,X_k=1.$$故$$\{T_1=k\}=\{X_1=\cdots =X_{k-1}=0,X_k=1\}.$$由 $X_1,X_2,\dots$ 的独立性可得$$\begin{array}{rl}\mathbb{P}(T_1=k)& =\mathbb{P}(X_1=\cdots =X_{k-1}=0,X_k=1)\\ & =\mathbb{P}(X_1=0)\cdots \mathbb{P}(X_{k-1}=0)\cdot \mathbb{P}(X_k=1)=(1-p{)}^{k-1}p,\end{array}$$从而 $T_1$ 的分布列为$$p_{T_1}(k)=(1-p{)}^{k-1}p,k=1,2,3,\dots$$这意味着 $T_1$ 服从参数为 $p$ 的几何分布.

几何分布的无记忆性. 考虑这样一个情形: 我们对前 $m$ 个时刻的随机变量 $X_1,\dots ,X_m$ 进行了观察, 发现它们的值均为 $0$ (也就是说, 前 $m$ 个时刻没有一次伯努利试验是成功的), 在这个条件下, 我们还需要等多长时间才能有一次成功的试验? 换句话说, 在给定 $T_1>m$ 的情况下, $T_1-m$ 的条件分布是怎样的?

相关的计算是较为直接的: 对任意正整数 $k$, 有$$\begin{array}{rl}& \mathbb{P}\left(T_1-m=k|T_1>m\right)\\ =& \frac{\mathbb{P}(T_1=m+k,T_1>m)}{\mathbb{P}(T_1>m)}=\frac{\mathbb{P}(T_1=m+k)}{\mathbb{P}(T_1>m)}\\ =& \frac{(1-p{)}^{m+k-1}p}{{\sum }_{r=m+1}^{\infty }(1-p{)}^{r-1}p}=\frac{(1-p{)}^{m+k-1}p}{(1-p{)}^m}=(1-p{)}^{k-1}p.\end{array}$$(2.6.2)不难发现上式最右端就等于 $\mathbb{P}(T_1=k)$. 换句话说, 已知 $T_1>m$ 的作用相当于把时间原点向右平移了 $m$ 个单位时间, 而 $n=m+1$ 时刻起试验成功与否对于前 $m$ 个时刻的结果是没有记忆的. 一般地, 给定一取值为正整数的随机变量 $X$, 若 $X$ 满足$$\mathbb{P}\left(X=m+k|X>m\right)=\mathbb{P}(X=k),\forall m,k\in {\mathbb{N}}_{+},$$我们就称随机变量 $X$ 具有无记忆性. 考虑到这里的随机变量 $T_1$ 是直接从伯努利过程中构造而来的, 其无记忆性是非常容易理解的, 但不难看出式 (2.6.2) 的推导过程仅利用了 $T_1$ 的概率分布而不涉及其具体构造, 因此无记忆性是任意服从几何分布的随机变量都具有的性质.

$T_k$ ($k\ge 2$) 的分布. 我们不妨直接求解 $(T_1,\dots ,T_k)$ 的联合分布: 令 $t_1,\dots ,t_k\in {\mathbb{N}}_{+}$ 任意, 并为了方便记 $s_k={\sum }_{i=1}^k{t}_i$. 注意到$$T_1=t_1,\dots ,T_k=t_k⟺\begin{array}{rl}& X_{s_1}=\cdots X_{s_k}=1\\ & \text{且对其它1≤n<sk有}{X}_n=0,\end{array}$$故$$\begin{array}{rl}\mathbb{P}(T_1=t_1,\dots ,T_k=t_k)& =p^k(1-p{)}^{s_k-k}\\ & =p^k(1-p{)}^{{\sum }_{i=1}^k{t}_i-k}\\ & =\prod _{i=1}^k\left((1-p{)}^{t_i-1}p\right).\end{array}$$不难由上式看出 $T_1,\dots ,T_k$ 独立同分布, 且均服从参数为 $p$ 的几何分布.

二项分布的泊松分布近似

现在我们考虑一个特殊情况: 设伯努利试验成功的概率 $p$ 非常小, 但另一方面, 我们关心的是 $n$ 很大时 $N_n$ 的分布情况. 若进一步假定 $n{p}^2$ 很小, 则在这种情形下, 我们可以给分布列 (2.6.1) 找一个更好用的近似计算式.

设 $k$ 是一个正整数, 满足 $k^2$ 远小于 $n$, 则有$$\begin{array}{rl}{p}_{N_n}(k)& =\frac{n(n-1)\cdots (n-k+1)}{k(k-1)\cdots 1}{p}^k{\left(1-p\right)}^{n-k}\\ & ={\left(1-p\right)}^{n-k}\frac{(np{)}^k}{k!}\cdot \prod _{i=0}^{k-1}\left(1-\frac{i}{n}\right).\end{array}$$接下来我们对上式右端做近似:

1.

为了对 ${\prod }_{i=0}^{k-1}\left(1-\frac{i}{n}\right)$ 取近似, 注意到$$1\ge \prod _{i=0}^{k-1}\left(1-\frac{i}{n}\right)\ge 1-\frac{{\sum }_{i=0}^{k-1}i}{n}=1-\frac{k(k-1)}{2n}.$$故 $k^2$ 远小于 $n$ 时 ${\prod }_{i=0}^{k-1}\left(1-\frac{i}{n}\right)$ 可以近似为 $1$.

2.

为了对 $(1-p{)}^{n-k}$ 取近似, 注意到$$\begin{array}{rl}\left|\ln \frac{(1-p{)}^{n-k}}{{\mathrm{e}}^{-np}}\right|& =\left|n(\ln (1-p)+p)-k\ln (1-p)\right|\\ & \le n|\ln (1-p)+p|+k|\ln (1-p)|\\ & \le \frac{1}{1-p}\left(n{p}^2+kp\right)=\frac{1}{1-p}\left(n{p}^2+\sqrt{\frac{k^2}{n}\cdot n{p}^2}\right)\\ & \le \frac{1}{1-p}\left(n{p}^2+\frac{k^2}{2n}+\frac{n{p}^2}{2}\right),\end{array}$$其中用到了不等式$$\frac{-p}{1-p}\le \ln (1-p)\le -p,\forall p<1.$$因此 $n{p}^2$ 与 $k^2/n$ 非常小时可以取近似$${\left(1-p\right)}^{n-k}\approx {\mathrm{e}}^{-(n-k)p}\approx {\mathrm{e}}^{-np}.$$

综上可得$$p_{N_n}(k)\approx {\mathrm{e}}^{-np}\frac{(np{)}^k}{k!}$$(2.6.3)不难看出上式右端与参数为 $np$ 的泊松分布相吻合. 这里再明确一下式 (2.6.3) 成立的条件: (i) $n$ 非常大; (ii) $n{p}^2$ 非常小; (iii) $k^2$ 远小于 $n$.

实际上, 由上面的计算过程不难证明如下命题:

命题 2.6.2. 给定 $\lambda >0$, 对任意足够大的正整数 $n$, 令 $p_n=\lambda /n$, 并令$$b(k;n,p_n)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)p_n^k(1-p_n{)}^{n-k},$$则对任意自然数 $k$, 有$$\underset{n\to \infty }{\lim }b(k;n,p_n)={\mathrm{e}}^{-\lambda }\frac{{\lambda }^k}{k!}.$$

基于以上结果, 我们通常会用泊松分布来对小概率事件在较长的一段时间内发生的次数进行建模.