3.5. 一般随机变量与分布函数

本节中, 我们对一般随机变量的理论进行简单介绍.

首先回答一个问题: 任一随机变量是否必定是离散型或连续型之一? 答案是否定的.

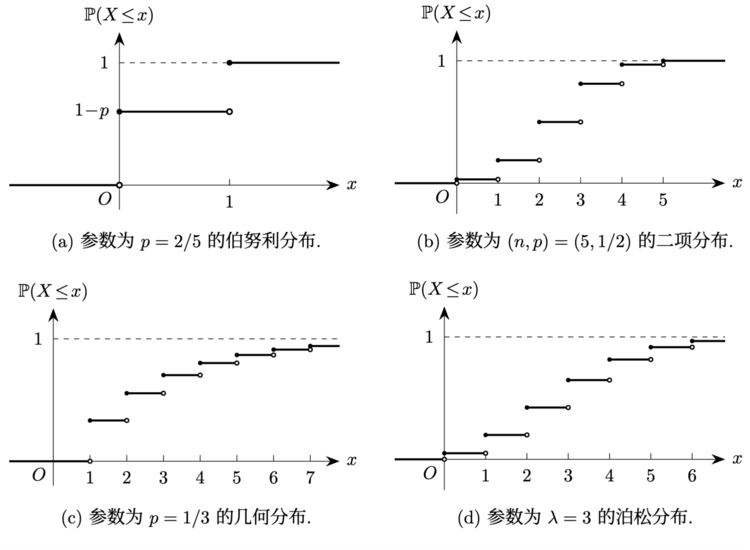
例 3.5.1. 设 $(\Omega ,\mathcal{F},\mathbb{P})$ 为一概率空间, 随机变量 $X:\Omega \to \{0,1\}$ 服从参数为 $1/2$ 的伯努利分布, 随机变量 $Y:\Omega \to \mathbb{R}$ 服从标准正态分布, $X$ 与 $Y$ 相互独立. 令随机变量 $Z$ 为$$Z(\omega )=\{\begin{array}{ll}0,& \text{若}X(\omega )=0,\\ Y(\omega ),& \text{若}X(\omega )=1,\end{array}\forall \omega \in \Omega .$$可以证明 $Z$ 不是连续性随机变量: 注意到$$\begin{array}{rl}\mathbb{P}(Z=0)& =\mathbb{P}(Z=0,X=0)+\mathbb{P}(Z=0,X=1)\\ & =\mathbb{P}(X=0)+\mathbb{P}(X=1,Y=0)\\ & =\mathbb{P}(X=0)+\mathbb{P}(X=1)\cdot \mathbb{P}(Y=0)\\ & =\frac{1}{2}+\frac{1}{2}\cdot 0=\frac{1}{2},\end{array}$$由于连续型随机变量取某个给定值的概率总是 $0$, 故 $Z$ 不是连续型随机变量. 但另一方面, 也可证明 $Z$ 不是离散型随机变量: 若 $Z$ 是离散型随机变量, 令其分布列为 $p_Z$, 则有 $p_Z(0)=\mathbb{P}(Z=0)=1/2<1$, 故必定存在 $z_0\ne 0$ 使得 $p_Z(z_0)>0$, 但若取充分小的 $\delta >0$ 使得 $0\notin \left]z_0-\delta ,z_0+\delta \right[$, 则有$$\begin{array}{rl}\mathbb{P}(Z=z_0)\le & \mathbb{P}(z_0-\delta <Z<z_0+\delta )=\mathbb{P}(z_0-\delta <Y<z_0+\delta ,X=1)\\ =& \mathbb{P}(z_0-\delta <Y<z_0+\delta )\cdot \mathbb{P}(X=1)=\frac{1}{2}{\int }_{z_0-\delta }^{z_0+\delta }\frac{1}{\sqrt{2\pi }}{\mathrm{e}}^{-y^2/2}\mathrm{d}y,\end{array}$$令 $\delta \to 0^{+}$ 即可得到 $\mathbb{P}(Z=z_0)=0$, 与 $p_Z(z_0)>0$ 矛盾.

例 3.5.2. (${}^{\star }$) 设 $(\Omega ,\mathcal{F},\mathbb{P})$ 为一概率空间, 随机变量 $X:\Omega \to \mathbb{R}$ 服从 $[0,1]$ 上的均匀分布. 任取 $\omega \in \Omega$, 将 $X(\omega )$ 展开为二进制小数 ¹$$X(\omega )=\sum _{n=1}^{\infty }\frac{a_n(\omega )}{2^n},a_n(\omega )\in \{0,1\},$$再令$$Y(\omega )=\sum _{n=1}^{\infty }\frac{2a_n(\omega )}{3^n}.$$由此可以得到一个随机变量 $Y:\Omega \to \mathbb{R}$. 可以证明, 对任意 $a\in \mathbb{R}$, 均有 $\mathbb{P}(Y=a)=0$, 故 $Y$ 不可能是一个离散型随机变量. 但也可以证明, 并不存在定义在 $\mathbb{R}$ 上的非负函数 $f$ 使得 $\mathbb{P}(Y\in I)={\int }_{I}f(x)\mathrm{d}x$, 因此 $Y$ 也不是一个连续型随机变量.

为了研究那些既非离散型也非连续型的随机变量, 并且也为了用一个统一的数学工具去刻画随机变量取值的统计规律, 我们引入分布函数的概念.

定义 3.5.3. 设 $X$ 为一随机变量, 令函数 $F_X:\mathbb{R}\to [0,1]$ 定义如下: $$F_X(x)=\mathbb{P}(X\le x),\forall x\in \mathbb{R}.$$我们称 $F_X$ 为随机变量 $X$ 的分布函数, 也称为累积分布函数 (cumulative distribution function, c.d.f).

对于任意的随机变量 $X$, 其分布函数 $F_X$ 都是有定义的, 这是因为随机变量的定义要求 $\{X\le x\}=\{X\in \left]-\infty ,x\right]\}$ 必须是一个事件, 从而其概率有定义. 后面我们将看到, 分布函数能够完整刻画单个随机变量的统计规律性, 并且大多数随机变量的数字特征 (包括期望、方差等) 仅依赖于其分布函数.

以下定理总结了分布函数所具有的基本性质.

定理 3.5.4. 设 $(\Omega ,\mathcal{F},\mathbb{P})$ 为一概率空间, $X:\Omega \to \mathbb{R}$ 为一随机变量, $F_X$ 为其分布函数. 则

1.	$F_X$ 在 $\mathbb{R}$ 上单调不减.
2.	$F_X(x)\in [0,1],\forall x\in \mathbb{R}$, 并且$$F_X(+\infty ):=\underset{x\to +\infty }{\lim }{F}_X(x)=1,F_X(-\infty ):=\underset{x\to -\infty }{\lim }{F}_X(x)=0.$$
3.	$F_X$ 在 $\mathbb{R}$ 上右连续, 即对任意的 $x\in \mathbb{R}$, 有$$F_X(x+0):=\underset{\delta \to 0^{+}}{\lim }{F}_X(x+\delta )=F_X(x).$$

定理 3.5.4 中分布函数单调不减的证明较为直接: 注意到 $x_1\le x_2$ 时有$$\begin{array}{rl}{F}_X(x_2)& =\mathbb{P}(X\le x_2)\\ & =\mathbb{P}(\{X\le x_1\}\cup \{x_1<X\le x_2\})\\ & =\mathbb{P}(X\le x_1)+\mathbb{P}(x_1<X\le x_2)=F_X(x_1)+\mathbb{P}(x_1<X\le x_2),\end{array}$$即$$\mathbb{P}(x_1<X\le x_2)=F_X(x_2)-F_X(x_1).$$再由概率的非负性可直接得到 $x_1\le x_2$ 时有 $F_X(x_2)-F_X(x_1)\ge 0$. $F_X(x)\in [0,1],\forall x\in \mathbb{R}$ 则是概率测度定义的直接推论. 其余性质的证明超出本课程的范围, 我们将其放在本节倒数第二小节作为选读内容.

定理 3.5.4 的逆定理也同样成立: 若函数 $F:\mathbb{R}\to \mathbb{R}$ 满足 (i) $F$ 在 $\mathbb{R}$ 上单调不减; (ii) $F(+\infty )=1$, $F(-\infty )=0$; (iii) $F$ 在 $\mathbb{R}$ 上右连续, 则存在一概率空间 $(\Omega ,\mathcal{F},\mathbb{P})$ 及随机变量 $X:\Omega \to \mathbb{R}$, 使得 $F$ 为 $X$ 的分布函数, 此时我们称函数 $F$ 给出了一个概率分布. 这个结论的证明不做要求.

分布函数 $F_X$ 直接给出了 $X\le x$ 的概率, 而 $X<x$ 的概率则由如下命题给出, 其证明放在本节最后一小节中作为选读内容:

命题 3.5.5. 设 $X$ 为一随机变量, $F_X$ 为其分布函数, $x\in \mathbb{R}$, 则有$$\begin{array}{rl}\mathbb{P}(X<x)& =F_X(x-0)=\underset{\delta \to 0^{+}}{\lim }{F}_X(x-\delta ).\end{array}$$

基于命题 3.5.5, 我们可以进一步由概率的可加性得到 $X$ 落于任意区间内的概率, 例如$$\mathbb{P}(a<X<b)=\mathbb{P}(X<b)-\mathbb{P}(X\le a)=F_X(b-0)-F_X(a).$$而对于更加一般的 $\mathbb{R}$ 的子集 $B$, 只要它可以表示为可数个互不相交的区间的并, 我们就可以利用概率的可数可加性来求得 $\mathbb{P}(X\in B)$. 在这个意义上, 我们可以说分布函数能够完整刻画单个随机变量的统计规律性.

对于离散型或连续型的随机变量 $X$, 不难由它的分布列 $p_X$ 或概率密度函数 $f_X$ 求出分布函数 $F_X$: $$F_X(x)=\{\begin{array}{ll}\sum _{t:t\le x}{p}_X(t),& \text{若 X 是离散型随机变量},\\ {\int }_{-\infty }^x{f}_X(t)\mathrm{d}t,& \text{若 X 是连续型随机变量},\end{array}$$而反过来, 给定 $X$ 的分布函数, 我们也可以去求它的分布列或概率密度函数:

•	当 $X$ 的值域是可数集, 即 $X$ 为离散型随机变量时, 其分布列为$$p_X(x)=F_X(x)-F_X(x-0),\forall x\in \mathbb{R}.$$
•	当 $F_X$ 为连续函数时, 令$$f(x)=\{\begin{array}{ll}{F}_X^{\prime }(x),& \text{若 FX 在 x 处可导},\\ 0,& \text{若 FX 在 x 处不可导},\end{array}\forall x\in \mathbb{R}.$$若进一步有 $F_X(x)={\int }_{-\infty }^{x}f(t)\mathrm{d}t$, 则 $X$ 是连续型随机变量, 上式算出的 $f$ 即为 $X$ 的概率密度函数; 否则 $X$ 不是连续型随机变量 2.

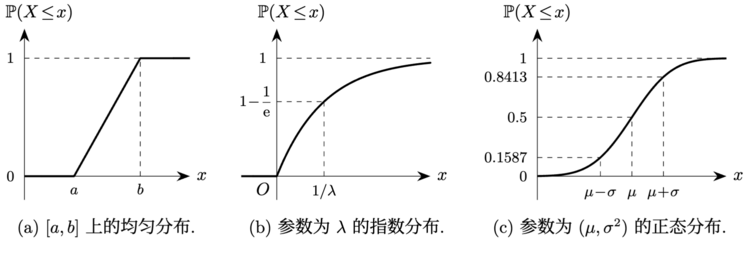
图 1 与 2 分别给出了一些离散型与连续型概率分布的分布函数图像.

图 1. 一些离散型概率分布的分布函数.

图 2. 一些连续型概率分布的分布函数.

例 3.5.6 (均匀分布的分布函数). 设 $X$ 服从区间 $[a,b]$ 上的均匀分布, 其中 $a<b$, 则其分布函数 $F_X$ 为$$F_X(x)=\{\begin{array}{ll}0,& x\le a,\\ \frac{x-a}{b-a},& a<x<b,\\ 1,& x\ge b.\end{array}$$它是一个分段线性函数, 其图像如图 2(a) 所示.

例 3.5.7 (指数分布的分布函数与无记忆性).

设 $X$ 服从参数为 $\lambda$ 的指数分布. 则其分布函数为$$F_X(x)=\{\begin{array}{ll}{\int }_0^x\lambda {\mathrm{e}}^{-\lambda t}\mathrm{d}t=1-{\mathrm{e}}^{-\lambda x},& \text{若}x\ge 0,\\ 0,& \text{若}x<0.\end{array}$$指数分布的分布函数图像如图 2(b) 所示.

指数分布具有如下意义上的无记忆性: 若 $X$ 服从参数为 $\lambda$ 的指数分布, 则对任意非负实数 $s,t$, 均有$$\mathbb{P}\left(X>s+t|X>s\right)=\frac{\mathbb{P}(X>s+t)}{\mathbb{P}(X>s)}=\frac{{\mathrm{e}}^{-\lambda (s+t)}}{{\mathrm{e}}^{-\lambda s}}={\mathrm{e}}^{-\lambda t}=\mathbb{P}(X>t).$$这意味着, 若我们把 $X$ 看成从零时刻开始到某件事情发生所需要等待的时间, 则已知 $X>s$ 的作用相当于把时间原点向右平移了 $s$, 而 $s$ 时刻以后所需要的额外的等待时间依然服从原来的指数分布, 它 “忘记” 了这件事情在 $s$ 时刻之前并未发生的这段历史.

例 3.5.8 (正态分布的分布函数). 设 $X\sim \mathcal{N}(0,1)$, 则其分布函数为$$F_X(x)=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^x\exp \left(-\frac{t^2}{2}\right)\mathrm{d}t,\forall x\in \mathbb{R}.$$等号右端的积分并没有初等函数表达式, 我们将它作为特殊函数处理, 记作$$\Phi (x)=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^x\exp \left(-t^2/2\right)\mathrm{d}t,x\in \mathbb{R}.$$

更一般地, 设 $X\sim \mathcal{N}(\mu ,{\sigma }^2)$, 则其分布函数为$$\begin{array}{rl}{F}_X(x)& ={\int }_{-\infty }^x\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{(t-\mu {)}^2}{2{\sigma }^2}\right)\mathrm{d}t\\ & =\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{(x-\mu )/\sigma }\exp \left(-\frac{u^2}{2}\right)\mathrm{d}u=\Phi \left(\frac{x-\mu }{\sigma }\right),\end{array}$$其中第二步做了换元 $u=(x-\mu )/\sigma$. 正态分布的分布函数图像如图 2(c) 所示.

随机向量的联合分布函数

对于一般的二维随机向量 $(X,Y)$, 我们可定义其联合分布函数 (又称作联合累积分布函数, joint cumulative distribution function, joint c.d.f.) 为$$F_{X,Y}(x,y)=\mathbb{P}(X\le x,Y\le y).$$该定义可以很容易推广到更高维的随机向量.

理论上可以证明, 只要已知分布函数 $F_{X,Y}$, 那么对于常见的平面上的区域 $B\subseteq {\mathbb{R}}^2$, 其概率 $\mathbb{P}((X,Y)\in B)$ 都能被唯一确定下来. 然而, 直接由 $F_{X,Y}$ 出发来计算 $\mathbb{P}((X,Y)\in B)$ 对于许多问题而言并不方便, 更常见的做法是先考察 $(X,Y)$ 是否是离散型或连续型随机向量并求出其联合分布列或联合概率密度, 或是以之后将要介绍的条件期望为工具进行求解. 本讲义中, 我们不对联合分布函数进行较为详细的介绍, 而仅罗列一些相关结论如下:

•	$(X,Y)$ 为连续型随机向量当且仅当其联合分布函数可表示为如下形式:$$F_{X,Y}(x,y)={\int }_{-\infty }^x\left({\int }_{-\infty }^y{f}_{X,Y}(s,t)\mathrm{d}t\right)\mathrm{d}s,\forall (x,y)\in {\mathbb{R}}^2.$$ 此外, 若已知 $(X,Y)$ 为连续型随机向量, 且 $F_{X,Y}$ 在某个平面上的开区域 $\mathcal{U}\subseteq {\mathbb{R}}^2$ 内二阶连续可导, 则有$$f_{X,Y}(x,y)=\frac{{\partial }^2{F}_{X,Y}}{\partial x\partial y}(x,y),\forall (x,y)\in \mathcal{U}.$$ 上述结果常用于求解连续型随机向量 $(X,Y)$ 的联合概率密度函数.
•	已知 $(X,Y)$ 的联合分布函数, 则 $X$ 与 $Y$ 各自的分布函数 (也就是边缘分布函数) 被唯一确定: $$\begin{array}{rl}{F}_X(x)& =\underset{y\to +\infty }{\lim }{F}_{X,Y}(x,y),\forall x\in \mathbb{R},\\ F_Y(y)& =\underset{x\to +\infty }{\lim }{F}_{X,Y}(x,y),\forall y\in \mathbb{R}.\end{array}$$
•	$X,Y$ 相互独立的充要条件是$$F_{X,Y}(x,y)=F_X(x)\cdot F_Y(y),\forall (x,y)\in {\mathbb{R}}^2,$$

(${}^{\star }$) 定理 3.5.4 其余结论的证明

记样本空间为 $\Omega$. 我们先证明 ${\lim }_{x\to +\infty }{F}_X(x)=1$. 注意到 $F_X(x)$ 为单调不减的函数, 因此只需证数列 ${\left(F_X(n)\right)}_{n=1}^{\infty }$ 在 $n\to \infty$ 时的极限为 $1$. 现对任意正整数 $n$, 令 $E_n=\{X\le n\}$, 则 $E_1,E_2,\dots$ 为递增的事件列, 且$$\begin{array}{rl}\underset{n\to \infty }{\lim }{E}_n=\bigcup _{n=1}^{\infty }{E}_n& =\left\{\omega \in \Omega \mid \text{存在正整数 n 使得 X(ω)≤n}\right\}=\Omega .\end{array}$$故由概率的连续性可得$$\begin{array}{rl}1& =\mathbb{P}(\Omega )=\underset{n\to \infty }{\lim }\mathbb{P}(E_n)=\underset{n\to \infty }{\lim }{F}_X(n).\end{array}$$

接下来证明 ${\lim }_{x\to -\infty }{F}_X(x)=0$. 注意到$$\begin{array}{rl}0\le F_X(x)& =\mathbb{P}(X\le x)=\mathbb{P}(-X\ge -x)\\ & \le \mathbb{P}(-X>-x-1)=1-\mathbb{P}(-X\le -x-1)\\ & =1-F_{-X}(-x-1),\end{array}$$而 $F_{-X}$ 作为随机变量 $-X$ 的分布函数满足 ${\lim }_{x\to +\infty }{F}_{-X}(x)=1$, 故令上式中 $x\to -\infty$ 即可得到 ${\lim }_{x\to -\infty }{F}_X(x)=0$.

最后我们证明 $F_X$ 的右连续性. 给定任意 $x\in \mathbb{R}$, 记 $G_n=\left\{X\le x+1/n\right\},\forall n\in {\mathbb{N}}_{+}$, 则 $G_1,G_2,\dots$ 为递减的事件列, 且$$\begin{array}{rl}\underset{n\to \infty }{\lim }{G}_n=\bigcap _{n=1}^{\infty }{G}_n=& \left\{\omega \in \Omega \mid \text{对任意正整数 n, 均有}X(\omega )\le x+\frac{1}{n}\right\}=\left\{X\le x\right\},\end{array}$$故由概率的连续性可得$$F_X(x)=\mathbb{P}(X\le x)=\underset{n\to \infty }{\lim }\mathbb{P}(G_n)=\underset{n\to \infty }{\lim }{F}_X\left(x+\frac{1}{n}\right).$$而 $F_X$ 的单调性保证了右极限 $F_X(x+0)$ 存在且等于 ${\lim }_{n\to \infty }{F}_X\left(x+1/n\right)$, 故 $F_X(x+0)=F_X(x)$.

(${}^{\star }$) 命题 3.5.5 的证明

记样本空间为 $\Omega$. 令$$E_n=\left\{X\le x-\frac{1}{n}\right\},n=1,2,\dots ,$$由于 $1/n$ 随 $n$ 的增大单调递减, 故 $E_n$ 成立时 $E_{n+1}$ 必定成立, 因此 $E_1,E_2,\dots$ 为一递增的事件列. 另一方面, $$\begin{array}{rl}\underset{n\to \infty }{\lim }{E}_n=& \bigcup _{n=1}^{\infty }{E}_n\\ =& \left\{\omega \in \Omega \mid \text{存在正整数 n 使得 }X(\omega )\le x-\frac{1}{n}\right\}\\ =& \left\{s\in S\mid X(s)<x\right\}=\{X<x\},\end{array}$$其中利用了 $n\to \infty$ 时 $1/n\to 0$. 故由概率的连续性可得$$\begin{array}{rl}\mathbb{P}(X<x)& =\mathbb{P}\left(\underset{n\to \infty }{\lim }{E}_n\right)=\underset{n\to \infty }{\lim }\mathbb{P}(E_n)=\underset{n\to \infty }{\lim }{F}_X\left(x-\frac{1}{n}\right)=F_X(x-0),\end{array}$$其中 $F_X(x-0)$ 的存在性由 $F_X$ 的单调性保证.

脚注

1.	^ (${}^{\star }$) 若存在正整数 $p,q$ 使得 $X(\omega )=p/2^q$, 则 $X(\omega )$ 存在两种二进制小数表示, 为明确起见, 这种情况下我们取 $n>q$ 时 $a_n(\omega )=0$ 的那种二进制小数表示.
2.	^ “否则” 部分的严格证明超出本讲义范围, 不做要求.