调和级数

调和级数是一个发散的级数, 表达式为: $$\sum _{k=1}^{\infty }\frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots$$

1发散性

比较审敛法

$$\begin{array}{rl}\sum _{k=1}^{\infty }\frac{1}{k}& =1+\left(\frac{1}{2}\right)+\left(\frac{1}{3}+\frac{1}{4}\right)+\left(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\right)+(\frac{1}{9}+\cdots \\ & \ge \sum _{k=1}^{\infty }{2}^{-\lceil {\log }_{2}k\rceil }\\ & =1+\left(\frac{1}{2}\right)+\left(\frac{1}{4}+\frac{1}{4}\right)+\left(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}\right)+(\frac{1}{16}+\cdots \\ & =1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\cdots =\infty .\end{array}$$

因此该级数发散.

积分判别法

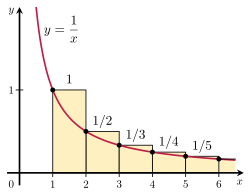
通过将调和级数的和与一个瑕积分作比较可证此级数发散. 考虑右图中长方形的排列. 每个长方形宽 1 个单位、高 $\frac{1}{n}$ 个单位 (换句话说, 每个长方形的面积都是 $\frac{1}{n}$) , 所以所有长方形的总面积就是调和级数的和: $$\text{矩形面积和}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\cdots .$$而曲线 $y=\frac{1}{x}$ 以下、从 1 到正无穷部分的面积由以下瑕积分给出: $$\text{曲线下面积}={\int }_1^{\infty }\frac{1}{x}dx=\infty .$$由于这一部分面积真包含于 (换言之, 小于) 长方形总面积, 长方形的总面积也必定趋于无穷. 更准确地说, 这证明了: $$\sum _{n=1}^k\frac{1}{n}>{\int }_1^{k+1}\frac{1}{x}dx=\ln (k+1).$$

2渐进展开

(...)

3相关概念

•	对数函数
•	Euler 常数

术语翻译

调和级数 • 英文 harmonic series • 德文 harmonische Reihe • 法文 série harmonique