整理《经典物理选讲》的笔记于此, 只做了一部分. 以后的人可以继续写下去, 谢谢.
牛顿力学 本章的参考材料为 [Li
质点运动
∘
位矢 r ( t )
∘
速度 v = r ˙ ( t )
∘
加速度 a = r ¨ = d t d v = d t 2 d 2 r
设平面上的点 ( x , y ) = ( r cos θ , r sin θ ) e r , e θ r , θ e r : = ( cos θ , sin θ ) , e θ : = − ( sin θ , cos θ ) .
e ˙ r = θ ˙ e θ , e ˙ θ = − θ ˙ e r . v = d t d ( r e r ) = r ˙ e r + r θ ˙ e θ , 即 v r = r ˙ , v θ = r θ ˙ .
a = d t d ( r ˙ e r + r θ ˙ e θ ) = r ¨ e r + r ˙ θ ˙ e θ + r ˙ θ ˙ e θ + r θ ¨ e θ + r θ ˙ ( − θ ˙ e r ) = ( r ¨ − r θ ˙ 2 ) e r + ( 2 r ˙ θ ˙ + r θ ¨ ) e θ , 即 a r = r ¨ − r θ ˙ 2 , a θ = 2 r ˙ θ ˙ + r θ ¨ = r 1 d t d ( r 2 θ ˙ ) .
当质点的轨道给定, 任取轨道上一点 Q Q P s P 弧坐标 .
设位矢为 r = r ( s ) v = d t d r = d s d r d t d s = s ˙ τ , τ ∣ τ ∣ = d s ∣ d r ∣ = 1 a = d t d ( s ˙ τ ) = s ¨ τ + s ˙ 2 d s d τ = s ¨ τ + ρ s ˙ 2 n , 曲率矢量 N = d s d τ = N n = ρ n . 主法线方向 , 通常指向直线弯曲的一侧, n N 曲率 , ρ 曲率半径 (是曲线内切圆的半径) , 于是有内秉方程 a τ = s ¨ = v ˙ = v d s d v , a n = ρ s ˙ 2 = ρ v 2 .
对于不同的轨道方程, 曲率半径为{ x = x ( t ) , y = y ( t ) , ⎩ ⎨ ⎧ x = x ( s ) , y = y ( s ) , z = z ( s ) , ρ = ∣ x ˙ y ¨ − x ¨ y ˙ ∣ ( x ˙ 2 + y ˙ 2 ) 3/2 ; ρ = x ¨ s 2 + y ¨ s 2 + z ¨ s 2 1 .
地面上有一半球形粗糙凹坑, 质点在坑边无初速地跌入, 求质点到达坑底的速度. 凹坑的半径为 R μ
解答. 从切向、法向的受力有⎩ ⎨ ⎧ m g cos θ − μ N N − m g sin θ = m d t d v , = m v 2 / R . N d t d v = g cos θ − μ ( g sin θ + v 2 / R ) , 2 R d t d v = 2 g R ( cos θ − μ sin θ ) − 2 μ v 2 . t 2 R d t d v = 2 R d t d θ d θ d v = 2 v d θ d v = d θ d ( v 2 ) , v 2 = z d θ d z + 2 μ z − 2 g R ( cos θ − μ sin θ ) = 0. e 2 μ θ e 2 μ θ d θ d z + 2 μ e 2 μ θ z = 2 g R ( cos θ − μ sin θ ) e 2 μ θ , θ e 2 μ θ z = g R ∫ 2 ( cos θ − μ sin θ ) e 2 μ θ . 2 ( cos θ − μ sin θ ) = e i θ + e − i θ + i μ ( e i θ − e − i θ ) = ( 1 + i μ ) e i θ + ( 1 − i μ ) e − i θ , e 2 μ θ z = g R ( i + 2 μ 1 + i μ e ( i + 2 μ ) θ + − i + 2 μ 1 − i μ e ( − i + 2 μ ) θ + C ) . θ = 0 z = v 2 = 0 C e 2 μ θ z = g R ( i + 2 μ 1 + i μ ( e ( i + 2 μ ) θ − 1 ) + − i + 2 μ 1 − i μ ( e ( − i + 2 μ ) θ − 1 ) ) . θ = 2 π e μ π z = g R ( i + 2 μ 1 + i μ ( i e μ π − 1 ) + − i + 2 μ 1 − i μ ( − i e μ π − 1 ) ) , v = z 1/2 = ( 1 + 4 μ 2 − 2 μ 2 − 3 μ e − μ π + 1 2 g R ) 1/2 . □
习题 1. 如图, 曲柄
O A 长为
r , 以恒定角速度
ω 绕定点
O 转动. 此曲柄借连杆
A B 使滑块
B 沿直线
O x 运动. 求连杆中点
C 的轨迹和速率.
解答. C 的坐标为
( r cos ϕ + a 2 − ( 2 r sin ϕ ) 2 , 2 r sin ϕ ) , ϕ = ω t , 速率为
∣ ( − r sin ϕ ω − 2 r 2 sin ϕ cos ϕ ω / a 2 − ( 2 r sin ϕ ) 2 , 2 r cos ϕ ω ) ∣ = r ω ( sin ϕ + 2 r sin ϕ cos ϕ / a 2 − ( 2 r sin ϕ ) ) 2 + ( 2 cos ϕ ) 2 . 习题 2. 质点作平面运动, 其速度为
v = p e x + q e θ , 其中
p , q 为常量, 且
q > p > 0 . 求极坐标轨道方程.
解答. 注意到e x = e r cos θ − e θ sin θ , r ˙ e r + r θ ˙ e θ = p ( e r cos θ − e θ sin θ ) + q e θ , { r ˙ r θ ˙ = p cos θ , = − p sin θ + q , r r ˙ = − p sin θ + q p cos θ θ ˙ , r ( − p sin θ + q ) = C . □
习题 3. 直线
FM 在一给定的椭圆平面内以匀角速
ω 转动. 求此直线与椭圆交点
M 的速度. 已知以焦点为坐标原点的椭圆的极坐标方程为
r = 1 + e cos θ a ( 1 − e 2 ) , 式中
a 为椭圆的长半轴,
e 为偏心率, 都是常数.
解答. r ˙ = 1 + e cos θ e sin θ r ω , v = 1 + e cos θ e sin θ r ω e r + r ω e θ , v = r ω ∣ ∣ ( 1 + e cos θ e sin θ , 1 ) ∣ ∣ = r ω 1 + e cos θ 1 + 2 e cos θ + e 2 . □
习题 8. 一质点沿着抛物线
y 2 = 2 q x 运动, 其切向加速度的量值为法向加速度量值的
2 k 倍, 如此质点从正交弦
( 2 q , q ) 的一段以速度
u 出发, 试求其达到正交弦另一端
( 2 q , − q ) 时的速率.
解答. 要a τ = 2 k a n , v d s d v = 2 k ρ v 2 , ρ = ∣ ∣ d θ d s ∣ ∣ θ x v d v = 2 k ρ d s = 2 k d θ , v = e 2 k θ + C . q y = q ( x + 2 q ) , − q y = q ( x + 2 q ) , θ = 4 π , θ = 4 3 π , v = u e kπ . □
习题 9. 质点沿着半径为
R 的圆周运动, 加速度与速度的夹角为
α , 初速度为
v 0 . 试证质点的速度可表示为
v = v 0 e ( θ − θ 0 ) c o t α .
证明. 要a τ = a n cot α , v ˙ = R v 2 cot α , v v ˙ = R v cot α = θ ˙ cot α , v = e θ c o t α + C , v = v 0 e ( θ − θ 0 ) c o t α . □
习题 15. 物体沿铅垂平面内开口向上的光滑摆线运动, 证明质点一定作简谐振动, 且周期与振幅的大小无关. 摆线的参数方程是
x = b ( 2 θ + sin 2 θ ) , y = b ( 1 − cos 2 θ ) . 提示: 用自然坐标.
证明. 由( x ˙ , y ˙ ) = ( b θ ˙ ( 2 + 2 cos 2 θ ) , b θ ˙ 2 sin 2 θ ) , v = b θ ˙ 2 ( 2 cos θ ) = 4 b ( sin θ ) ′ . a τ = − g sin θ , a τ = v ˙ = 4 b ( sin θ ) ′′ , sin ( 2 g b θ ) = C sin ( t − t 0 ) , T = 2 π g b . □
质点力学 一个质点在惯性系中所受的力通常可表示为 r , r ˙ , t m r ¨ = F ( r , r ˙ , t ) . 约束 , 这种运动叫作约束运动 . 这实际上是产生约束的物体 (称为约束物体 ) 对质点提供的反作用力, 通常是弹性力. 相应的微分方程是m r ¨ = F ( r , r ˙ , t ) + R .
解算约束运动, 一般用内秉方程方便, 对于表面光滑的曲线, 取
τ , n , b 为右手坐标系, 有
m d t d v m r v 2 0 = F τ , = F n + R n , = F b + R b . 引入动量 p = m v , F = m a F = d t d p , 动量定理 , 在广义相对论下仍然成立, 尽管那时 m
当 F = 0 p = 常数 , 动量守恒定律 . 当某个直角坐标分量 F x = 0 p x = 常数 . 冲量 等于动量的增加, 系冲量 : = ∫ t 1 t 2 F d t = Δ p .
根据动量定理, 有
r × F = r × d t d p = d t d ( r × p ) − d t d r × p , 右端第二项即
v × m v = 0 . 引入以下概念:
∘
力矩 M = r × F
∘
角动量 J = r × p = r × m r ˙
可得
角动量定理 M = d t d J . 若
M = 0 , 则
J = 常数, 这称为
角动量守恒定律 ; 特别地, 若
F / / r , 则角动量守恒.
再根据动量定理, 有r ⋅ F = r ⋅ d t d p = d t d ( r ⋅ p ) − d t d r ⋅ p = d t d ( r ⋅ p ) − 2 T , T = 2 1 m v 2 动能 . 移项有r ⋅ F + 2 T = d t d ( r ⋅ p ) , r , p τ τ 1 ∫ t 0 t 0 + τ ( r ⋅ F ) d t = τ 1 r ⋅ p ∣ ∣ t 0 t 0 + τ , τ → ∞ 0 T = − 2 1 r × F , 位力原理 .
运动参考系 经典力学是建立在伽利略和牛顿所提出的绝对时空观基础之上的, 按照绝对时空观, 两个处在不同参考系中的观察者, 所观测到的空间距离和时间间隔不会因参考系的相对运动而存在差异.
平动参考系 设参考系 S ′ S O O ′ = r 0 S 静止参考系 , S ′ 运动参考系 . 由r = r ′ + r 0 , v = v ′ + v 0 . v 绝对速度 , v ′ 相对速度 , v 0 牵连速度 , 又有a = a ′ + a 0 . a 绝对加速度 , a ′ 相对加速度 , a 0 牵连加速度 . 于是得到 S F = m a + m a 0 , S ’ F + G = m a ′ , G = − m a 0 惯性力 .
转动参考系 参考系绕轴线以角速度 ω O 角速度矢量 ω v = ω × r 牵连速度 , 成立∣ v ∣ = ∣ ω × r ∣ = ∣ ω ∣∣ r ∣ sin θ = ∣ ω ∣ R . S ′ S S ′ ω S S ′ z
取任意矢量 P S ′ P = P x ′ e x ′ + P y ′ e y ′ + P z ′ e z ′ , d r d P = ( d t d P x ′ e x ′ + d t d P y ′ e y ′ + d t d P z ′ e z ′ ) + ( P x ′ d t d e x + P y ′ d t d e y + P z ′ d t d e z ) , d t d e x ′ = ω × e x ′ , d t d e x ′ = ω × e x ′ , d t d e x ′ = ω × e x ′ , d t d P = d t d ′ P + ω × P , d t d ′ P = d t d P x ′ e x ′ + d t d P y ′ e y ′ + d t d P z ′ e z ′ 相对变化率 , 是 P S ′ ω × P 相对变化率 , d t d P 绝对变化率 .
取 P = r v = v ′ + ω × r , 绝对速度 v 相对速度 v ′ ω × r 转动牵连速度 . d t d v = d t d v ′ + d t d ω × r + ω × v = ( d t d ′ v ′ + ω × v ′ ) + d t d ω × r + ω × ( v ′ + ω × r ) = d t d ′ v ′ + d t d ω × r + ω × ( ω × r ) + 2 ω × v ′ , 绝对加速度 a = d t d v 相对加速度 a ′ = d t d ′ v ′ d t d ω × r 转动牵连加速度 , ω × ( ω × r ) 向轴加速度 , 2 ω × v ′ 科里奥利加速度 .
于是得到 S ′ m a ′ = F − m d t d ω × r − m ω × ( ω × r ) − 2 m ω × v ′ ,
∘
− m d t d ω × r S ′ ω
∘
− m ω × ( ω × r ) 惯性离心力 ;
∘
− 2 m ω × v ′ 科里奥利力 , 在地球表面引起一系列的效应: 气旋, 河岸冲刷, 铁轨磨损, 落体东偏等.
一般参考系 下面来研究地球运动所引起的效应, 地球是匀速自转的非惯性系. 把坐标放在 S ′ = O ′ x ′ y ′ z ′ O O ′ = R OP = r O ′ P = r ′ d t d ω = 0 ∣ r ′ ∣ ≪ ∣ R ∣ r ≈ R a = a ′ + ω × ( ω × R ) + 2 ω × v ′ . m a ′ = F − m ω × ( ω × R ) − 2 m ω × v ′ .
设物体在纬度 λ h z x y m r ¨ = m g − 2 m ω × v . ω = ( − ω cos λ , 0 , ω sin λ ) , v = ( x ˙ , y ˙ , z ˙ ) , ω × v = ( − y ˙ ω sin λ , ω cos λ z ˙ + ω sin λ x ˙ , − ω cos λ y ˙ ) , ⎩ ⎨ ⎧ m x ¨ m y ¨ m z ¨ = 2 m y ˙ ω sin λ , = − 2 m ( ω cos λ z ˙ + ω sin λ x ˙ ) , = − m g + 2 mω cos λ y ˙ , 即 ⎩ ⎨ ⎧ x ¨ y ¨ z ¨ = 2 y ˙ ω sin λ , = − 2 ω ( cos λ z ˙ + sin λ x ˙ ) , = − g + 2 ω cos λ y ˙ . h ≪ R ω x ˙ , ω y ˙ ⎩ ⎨ ⎧ x ¨ y ¨ z ¨ = 0 , = − 2 w cos λ z ˙ , = − g . ( x ( 0 ) , y ( 0 ) , z ( 0 )) ( x ˙ ( 0 ) , y ˙ ( 0 ) , z ˙ ( 0 )) = ( 0 , 0 , h ) , = ( 0 , 0 , 0 ) , ⎩ ⎨ ⎧ x y z = 0 , = 3 1 ω g t 3 cos λ , = h − 2 1 g t 2 . t y 2 = − 9 8 g ω 2 cos 2 λ ( z − h ) 3 . z = 0 y = 3 1 g 8 h 3 ω cos λ . λ = 4 5 ∘ h = 100 y ≈ 1.535
习题 22. 位于竖直平面里的光滑滑钢丝圈的半径为 r m a v ′ R θ x
解答. 功能原理表明( m g − ma ) ( r cos θ 0 − r cos θ ) = 2 1 m v ′2 − 2 1 m v 0 ′ 2 , v ′ = v 0 ′ 2 + 2 ( g − a ) ( r cos θ 0 − r cos θ ) . R = r m v ′2 − ( m g − ma ) cos θ , R = r m v 0 ′ 2 + ( m g − ma ) ( 2 cos θ 0 − 3 cos θ ) . □
习题 23. 竖直的 O x y y = f ( x ) O x y y ω m O
解答. 约束力 R f ′ ( x ) = m g m ω 2 x , f ( x ) = 2 g ω 2 x 2 . R R = m g 2 + ( ω 2 x ) 2 . □
习题 24. 一质点在北纬
λ 处自地面竖直上抛, 它到达的最大高度为
h , 求它回至地面时, 相对于初位置的偏离.
解答. 以最高时为 t = 0 t = t 0 < 0 t = t 1 > 0 ( x ( t 0 ) , y ( t 0 ) , z ( t 0 )) x ˙ ( t 0 ) = y ˙ ( t 0 ) z ( 0 ) = h , z ˙ ( 0 ) = ( 0 , 0 , 0 ) , = 0 , = 0 , ⎩ ⎨ ⎧ x y z = 0 , = ω g cos λ ( 3 1 g t 3 − 2 1 t 0 t 2 + 6 1 t 0 3 ) , = h − 2 1 g t 2 . z = 0 − t 0 = t 1 = g 2 h y ( t 0 ) = − y ( t 1 ) = 2 ω g cos λ g 3 8 h 3 = 3 2 ω cos λ g 8 h 3 , y = y ( t 1 ) − y ( t 0 ) = − 3 4 ω cos λ g 8 h 3 . □
习题 25. 在北纬
λ 处以仰角
α 向东抛出一质点, 因地球的自转, 质点的落地点将发生向南的横向偏移, 证明偏移量为
g 2 4 v 0 3 ω sin λ sin 2 α cos α . 式中
ω 是地球自转角速度,
v 0 为质点初速度.
证明. 由近似 ω y ˙ ≪ g , ω ≪ v 0 ⎩ ⎨ ⎧ x ¨ y ˙ z ¨ = 2 y ˙ ω sin λ , = v 0 cos α , = − g , ( x ˙ ( 0 ) , y ˙ ( 0 ) , z ˙ ( 0 )) = ( 0 , v 0 cos α , v 0 sin α ) , ⎩ ⎨ ⎧ x y z = ω v 0 cos α sin λ t 2 , = v 0 cos α t , = − 2 1 g t 2 + v 0 sin α , t = g 2 v 0 sin α x ( t ) = ω cos α sin λ g 2 4 v 0 3 sin 2 α . □
拉格朗日力学 本章参考材料为 [Ar
变分法 变分学可以参考 [Zh
C 1 C 1 ([ t 0 , t 1 ]) ∥ γ ( t ) ∥ C 1 = t ∈ [ t 0 , t 1 ] max ∣ γ ( t ) ∣ + ∣ γ ′ ( t ) ∣
令 X = { x = x ( t ) ∈ C 1 ([ t 0 , t 1 ] ; R n ) ∣ x ( t 0 ) = x 0 , x ( t 1 ) = x 1 }
γ ∈ C 2 ([ t 0 , t 1 ] ; R n ) ∩ X Φ ( x ) = ∫ t 0 t 1 L ( x , x ˙ , t ) d t X x = γ ( t ) d t d ∂ x ˙ ∂ L = ∂ x ∂ L , ∀ t ∈ [ t 0 , t 1 ] .
为此, 需要两个准备工作:
(i) Φ 的微分 . Φ ( x ) = ∫ t 0 t 1 L ( x , x ˙ , t ) d t C 1 ([ t 0 , t 1 ]) F ( h ) = ∫ t 0 t 1 [ ∂ x ∂ L − d t d ∂ x ˙ ∂ L ] h d t + ( ∂ x ˙ ∂ L h ) ∣ ∣ t 0 t 1 . Φ ( x + h ) − Φ ( x ) = ∫ t 0 t 1 [ L ( x + h , x ˙ + h ˙ , t ) − L ( x , x ˙ , t ) ] d t = ∫ t 0 t 1 [ ∂ x ∂ L h + ∂ x ˙ ∂ L h ˙ ] d x + O ( h 2 ) = ∫ t 0 t 1 [ ∂ x ∂ L − 分部积分得到 d t d ∂ x ˙ ∂ L ] h d t + ( ∂ x ˙ ∂ L h ) ∣ ∣ t 0 t 1 + O ( h 2 ) . (ii) 一个标准的引理 . f ∈ C ([ t 0 , t 1 ]) h ( t 0 ) = h ( t 1 ) = 0 h ∈ C 1 ([ t 0 , t 1 ]) C ∞ ([ t 0 , t 1 ]) ∫ t 0 t 1 f h = 0 f ≡ 0
对任意
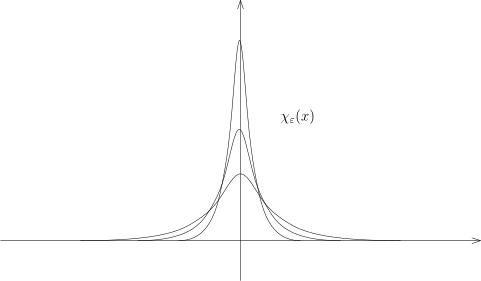
t ∗ ∈ ( t 0 , t 1 ) , 取
h ( t ) = χ ε ( t − t ∗ ) , 其中
{ χ ε } ε → 0 是逼近恒等 (如图) , 即得
f ( t ∗ ) = 0 .
2.1 的证明. 对
x ∈ X , 对一切适合
h ( t 0 ) = h ( t 1 ) = 0 的
h ∈ C 1 ([ t 0 , t 1 ]) 有
x + h ∈ X , 则
F ( h ) = 0 . 由 (i) 的表达式, 其中第二项为零, 有
∫ t 0 t 1 [ ∂ x ∂ L − d t d ∂ x ˙ ∂ L ] h d t = 0. 又由 (ii), 得证.
当 L t L = L ( x , x ˙ ) H ( x , x ˙ ) = x ˙ ∂ x ˙ ∂ L − L
证明. 直接计算有
d t d H ( x , x ˙ ) = x ˙ d t d ∂ x ˙ ∂ L + x ¨ ∂ x ˙ ∂ L − x ˙ ∂ x ∂ L − x ¨ ∂ x ˙ ∂ L = x ˙ [ d t d ∂ x ˙ ∂ L − ∂ x ∂ L ] = 0. 注: 这即是定理
2.13 . 下面的两题要用, 所以提前给出.
习题 1. 设平面与地平面垂直, A , B y A > y B x A = x B M A B A B T A B A B y = y ( x ) T A B ( y ( x )) T A B
解答. 设
A 为原点, 根据功能原理,
m g y = 2 1 m v 2 , 即
v = 2 g y . 为了计算
t 关于
x 的变化率, 设
M 走了长度
s , 有
d x d t = d x d s / d t d s = 2 g y 1 + y ˙ 2 . 故
T A B = ∫ t A t B d t = ∫ x A x B 2 g y 1 + y ˙ 2 d x . E–L 方程是
0 = d x d ∂ y ˙ ∂ L − ∂ y ∂ L = d x d 2 g y 1 + y ˙ 2 y ˙ + 2 2 g y y 1 + y ˙ 2 . 由于 Hamilton 量守恒,
2 g y 1 + y ˙ 2 y ˙ 2 − 2 2 g y 1 + y ˙ 2 = C , 化为
y ( 1 + y ˙ 2 ) = C /2. 换元
y = C ( 1 − cos θ ) , 得
1 + y ˙ 2 = 2 ( 1 − cos θ ) 1 = 1 + cot 2 2 θ , 于是
cot 2 θ = y ˙ = C sin θ θ ˙ , 那么
d θ d x = 1/ θ ˙ = C ( 1 − cos θ ) , 故曲线的参数方程为
{ x y = C ( θ − sin θ ) , = C ( 1 − cos θ ) , θ ∈ [ 0 , Θ ] , 其中
C , Θ 由
B 的坐标给出.
习题 2. (旋转极小曲面) 在平面上给定两点 P 1 = ( x 1 , y 1 ) , P 2 = ( x 2 , y 2 ) y 1 , y 2 > 0 x 1 < x 2 u ∈ C 1 [ x 1 , x 2 ] x
解答. 面积为
S = 2 π ∫ x 1 x 2 u ( x ) 1 + u ˙ ( x ) 2 d x . 由于 Hamilton 量守恒,
1 + u ˙ 2 u u ˙ 2 − u 1 + u ˙ 2 = C , 化为
( u / C ) 2 − 1 u ˙ = 1 , 积分得
u = C cosh ( C x + C ′ ) , 其中
C , C ′ 由边界点给出.
拉格朗日方程组 我们把下面两个方程相比较:
∘
牛顿方程 d t d ( m i r ˙ i ) + ∂ r i ∂ U = 0
∘
拉格朗日方程 d t d ∂ r ˙ ∂ L = ∂ r ∂ L
力学系统的运动恰好是 Φ ( γ ) = ∫ t 0 t 1 L d t L = T − U = 2 1 m i r ˙ i 2 − U ( r ) .
证明. γ Φ ( γ ) = ∫ t 0 t 1 L d t d t d ∂ r ˙ ∂ L = ∂ r ∂ L L = 2 1 m i r ˙ i 2 − U ( r i ) d t d ( m i r ˙ i ) = − ∂ r i ∂ U . □
这一原理能立即推广到任意一组坐标, 也就是说不一定要用欧式坐标 r i ( i = 1 , ⋯ , n ) q i ( i = 1 , ⋯ , n ) R 3 r , θ , φ L q i q ˙ i L = L ( q , q ˙ , t ) γ Φ d t d ∂ q ˙ i ∂ L = ∂ q i ∂ L , i = 1 , ⋯ , n .
对于力学系统的 L ∂ r ˙ i ∂ L = m i r ˙ i = p i , ∂ r i ∂ L = − ∂ r i ∂ U = F i . q i q i 广义坐标 , q ˙ i 广义速度 ) , 定义广义动量 和广义力 为∂ q ˙ i ∂ L = p i , ∂ q i ∂ L = F i . p ˙ i = F i .
习题 3. 证明在连接 A = r ( t 0 ) , B = r ( t 1 ) A B ∫ t 0 t 1 ( q ˙ 1 2 + q ˙ 2 2 + q ˙ 3 2 ) d t
证明. 用 E–L 方程求
E = ∫ t 0 t 1 ( q ˙ 1 2 + q ˙ 2 2 + q ˙ 3 2 ) d t 的极值点, 有
0 = d t d ∂ q ˙ i ∂ L − ∂ q i ∂ L = 2 q ˙ i , 于是
q i 均为常数, 曲线
r 是线段
A B . 这时
E 是最小值是因为, 对任意光滑曲线
r 都有
E ( r ) = ∫ t 0 t 1 ( q ˙ 1 2 + q ˙ 2 2 + q ˙ 3 2 ) d t ≥ t 1 − t 0 1 ( ∣ ∣ ∫ t 0 t 1 q ˙ 1 d t ∣ ∣ 2 + ∣ ∣ ∫ t 0 t 1 q ˙ 2 d t ∣ ∣ 2 + ∣ ∣ ∫ t 0 t 1 q ˙ 3 d t ∣ ∣ 2 ) = t 1 − t 0 1 ∣ A B ∣ 2 = E ( A B ) . 考虑有心力场中的平面运动. 用极坐标 q 1 = r , q 2 = θ T = 2 1 m v 2 = 2 1 m ( r ˙ 2 + r 2 θ ˙ 2 ) , L = 2 1 m ( r ˙ 2 + r 2 θ ˙ 2 ) − U ( r ) . p 1 = ∂ r ˙ ∂ L = m r ˙ , p 2 = ∂ θ ˙ ∂ L = m r 2 θ ˙ . p ˙ 1 = ∂ L / ∂ r m r ¨ = m r θ ˙ 2 − ∂ r ∂ U . L θ p ˙ 2 = ∂ L / ∂ θ = 0 p 2 =
(一般地说, 若场不是有心场, 即 U = U ( r , θ ) p ˙ 2 = − ∂ θ ∂ U
这个例子启示我们把角动量守恒定律推广如下.
对 L = L ( q 1 , ⋯ , q n , q ˙ 1 , ⋯ , q ˙ n , t ) L q i ∂ q i ∂ L = 0 q i 循环坐标 .
对应于循环坐标的广义动量守恒, 即 p i =
证明. d t d p i = d t d ∂ q ˙ i ∂ L = ∂ q i ∂ L = 0 .
勒让德变换 在集合 S = { f ( x ) ∈ C ∞ ( R ) ∣ f ′′ ( x ) > 0 , f ( x ) 超线性 } f ( x ) L f p g L f : = g ( p ) = x ∈ R sup ( p x − f ( x ) ) .
设 α , β > 1 1/ α + 1/ β = 1 f ( x ) = x α / α g ( p ) = x ∈ R sup ( p x − x α / α ) = ( p x − x α / α ) ∣ ∣ p = x α − 1 = p β / β .
f S f ∈ S L f ∈ S L 2 = id
Hamilton 函数 H ( p , q , t ) = p q ˙ − L ( q , q ˙ , t )
Lagrange 方程组等价于 2 n p ˙ = − ∂ q ∂ H , q ˙ = ∂ p ∂ H .
证明. 对
H 的表达式两边取微分, 得
∂ q ∂ L = − ∂ q ∂ H , q ˙ = ∂ p ∂ H . 故 Hamilton 方程组的前
n 个等价于
p ˙ = ∂ q ∂ L , 后
n 个自动成立.
d t d H = ∂ t ∂ H H t ∂ t ∂ H = 0 H ( p , q ) =
证明. d t d H = ∂ p ∂ H ⋅ ( − ∂ q ∂ H ) + ∂ q ∂ H ⋅ ∂ p ∂ H + ∂ t ∂ H = ∂ t ∂ H . □
刘维尔定理 设常微分方程x ˙ = f ( x ) , x ∈ R n , 相流 是单参数变换群g t : x ( 0 ) ↦ x ( t ) .
令 D ( 0 ) x v ( 0 ) v ( t ) D ( t ) D ( t ) = g t D ( 0 ) div f = 0 v ( t ) = v ( 0 )
证明. v ( t ) = ∫ D ( t ) d x = ∫ g t D ( 0 ) d x = ∫ D ( 0 ) ∣ ∣ det ∂ x ∂ g t x ∣ ∣ d x , g t x = x + f ( x ) t + O ( t 2 ) ⇒ ∂ x ∂ g t x = I + ∂ x ∂ f t + O ( t 2 ) ∣ ∣ det ∂ x ∂ g t x ∣ ∣ = 1 + tr ∂ x ∂ f t + O ( t 2 ) = 1 + div f t + O ( t 2 ) , v ( t ) = ∫ D ( 0 ) 1 + div f t + O ( t 2 ) d x . div f = 0 d t d v ( t ) = ∫ D ( 0 ) div f d x = 0. □
特别地, 对哈密顿方程组有
div H = ∂ p ∂ ( − ∂ q ∂ H ) + ∂ q ∂ ( ∂ p ∂ H ) = 0. 习题 1. 对线性方程组 x ˙ = A ( t ) x W W = W 0 e ∫ tr A d t
证明. W ∂ x ∂ x 1 ( t ) , ⋯ , ∂ x ∂ x n ( t ) V W ( t + Δ t ) = ∫ V ( t + Δ t ) d x = ∫ g Δ t V ( t ) d x = ∫ V ( t ) det ∂ x ∂ g Δ t x d x . det ∂ x ∂ g Δ t x = 1 + tr A ( t ) Δ t + O (( Δ t ) 2 ) , d t d W ( t ) = ∫ V ( t ) tr A ( t ) d x = tr A ( t ) W ( t ) . □
习题 2. 证明哈密顿方程在相空间中不可能有渐近稳定点.
证明. 设稳定点存在, 以之为原点, 对哈密顿方程组的固定的初值很小的解, 由于
A ( t ) = ( 0 I n − I n 0 ) ,
tr A = 0 ,
W 为非零常数; 稳定点又说当
t → ∞ 时
W → 0 , 矛盾.
庞加莱回归定理 ( X , S , μ ) f : X → X ∀ E ∈ I μ ( f − 1 ( E )) = μ ( E ) ∀ E ∈ S E f n x ∈ / E , ∀ n > 0
证明. 令 A n = k = n ⋃ ∞ { x ∈ X : f k x ∈ E } = k = n ⋃ ∞ f − k ( E ) E ⊂ A 0 A i ⊂ A j A i = f j − i A j j ≤ i
对于
n > 0 ,
μ ( E − A n ) ≤ μ ( A 0 − A n ) = μ ( A 0 ) − μ ( A n ) = 0 . 特别地,
μ ( E − A 1 ) = 0 .
习题 1. 验证 A i = f j − i A j j ≤ i
证明. f j − i A j = f j − i k = j ⋃ ∞ f − k ( E ) = k = i ⋃ ∞ f − k ( E ) = A i .
习题 2. 事实上 E
证明. μ ( E − n = 1 ⋂ ∞ A n ) = μ ( n = 1 ⋃ ∞ ( E − A n ) ) = 0 .
设 D ⊂ R n g : D → D D x 0 U x ∈ U , n ≥ 1 g n x ∈ U
证明. ∀ D 中可测集
E ,
μ ( g − 1 ( E )) = μ ( g ( g − 1 ( E ))) = μ ( E ) , 从而满足前一定理的条件, 所以不回归点零测, 更不能有开邻域那样大.
设 γ { γ } , { 2 γ } , ⋯ , { nγ } , ⋯ [ 0 , 1 )
证明见 [SS
习题 3. 2 n 1 , 2 , 4 , 8 , 1 , 3 , 6 , ⋯ 7 8 log 9 − log 8 log 8 − log 7
证明. { n lg 2 } [ 0 , 1 ) # { { n lg 2 } ∈ [ lg 7 , lg 8 ) : 1 ≤ n ≤ N } / N → lg 8 − lg 7 = lg e ( log 8 − log 7 ) , # { { n lg 2 } ∈ [ lg 9 , lg 8 ) : 1 ≤ n ≤ N } / N → lg 9 − lg 8 = lg e ( log 9 − log 8 ) . □
近几十年来, Furstenberg 把庞加莱回归定理推广为如下的多重回归定理:
设 ( X , S , μ ) T 1 , ⋯ , T l E ∈ S μ ( E ) > 0 n μ ( E ∩ T 1 − n E ∩ ⋯ ∩ T l − n E ) > 0
由此有下面的推论, 这两个结论具体参考 [
Fu ] 3.7 节 (p.77) . 设
S 是
Z 的子集, 称
S 的
上 Banach 密度 为
区间 ∣ I ∣ → ∞ lim sup ∣ I ∣ ∣ S ∩ I ∣ . 设 S Z S
诺特定理 Fraulein Noether was the most significant creative mathematician thus far produced since the higher education of women began.
— Albeit Einstein
∘
∘
若系统 ( M , L ) h s : M → M , s ∈ R L I : TM → R M q I I ( q , q ˙ ) = ∂ q ˙ ∂ L d s d h s ( q ) ∣ ∣ s = 0 .
证明. 仅对 M = R n q = q ( t ) : R → M Φ ( s , t ) = h s ( q ( t )) h s ∀ s ∈ ( − 1 , 1 ) h s ( q ( t )) d t d ∂ q ˙ ∂ L = ∂ q ∂ L ( ∗ )
目标证明
d t d ( ∂ q ˙ ∂ L ( Φ , Φ ˙ ) d s d Φ ) = 0 , 用
˙ 记对
t 的导数, 用
′ 记对
s 的导数, 即
d t d ( ∂ q ˙ ∂ L ( Φ , Φ ˙ ) ) Φ ′ + ∂ q ˙ ∂ L ( Φ , Φ ˙ ) d t d Φ ′ = 0. 由
( ∗ ) , 这等价于
∂ q ∂ L ( Φ , Φ ˙ ) Φ ′ + ∂ q ˙ ∂ L ( Φ , Φ ˙ ) d t d Φ ′ = 0. h s 为容许映射表明
∂ s ∂ L ( Φ , Φ ˙ ) = 0 , 此即上式.
习题 4. 若系统 ( R n , L ) h s : R n → R n , ∀ s q ( t ) L ∀ s ∈ ( − 1 , 1 ) h s ( q ( t )) L
证明. 记
S = ∫ L ( q , q ˙ ) , 有
S ( q + h ) − S ( q ) = O ( h 2 ) , 于是
S ( h s ( q + h )) − S ( h s q ) = O ( h 2 ) = O (( h s h ) 2 ) , 故
h s q 也是
L 对应的拉格朗日方程的解.
哈密顿力学 本章参考材料为 [MR
线性辛空间上的哈密顿系统 设 Z Ω : Z × Z → R Z Ω ♭ : Z → Z ∗ , z → Ω ( z , ⋅ ) Ω ♭ ∀ z 2 ∈ Z , Ω ( z 1 , z 2 ) = 0 z 1 = 0 Ω Ω ♭ Ω
向量空间 Z Ω Z ( Z , Ω )
( R 2 n , J ) J ( u , v ) = ⟨ u , J v ⟩ R 2 n J = ( 0 − I n I n 0 )
设 W W ′ Z = W × W ′ Z Ω (( w 1 , α 1 ) , ( w 2 , α 2 )) = α 2 ( w 1 ) − α 1 ( w 2 )
设 W Z = W × W Z Ω (( w 1 , w 2 ) , ( z 1 , z 2 )) = ⟨ z 2 , w 1 ⟩ − ⟨ z 1 , w 2 ⟩
∀ z , w ∈ C n z = x + i y , w = u + i v z ⋅ w ˉ = ( x + i y ) ⋅ ( u − i v ) = ( x , y ) ⋅ ( u , v ) − i ( x ⋅ v − y ⋅ u ) , Re ( z ⋅ w ˉ ) = ( x , y ) ⋅ ( u , v ) R 2 n − Im ( z ⋅ w ˉ ) = x ⋅ v − y ⋅ u = Ω (( x , y ) , ( u , v ))
复 Hilbert 空间 H H = L 2 ( R n ) Ω ( ψ 1 , ψ 2 ) = − 2ℏ Im ⟨ ψ 1 , ψ 2 ⟩ ℏ
辛几何初步 设 V 2 n 2 n Ω : V 2 n × V 2 n → R 2 ( V 2 n , Ω ) 2 ξ η Ω ( ξ , η ) = 0 ξ ⊥ η
R 2 n Ω (( u 1 , u 2 ) , ( v 1 , v 2 )) = v 2 ⋅ u 1 − v 1 ⋅ u 2
V 2 n 2 n e p 1 , ⋯ , e p n , e q 1 , ⋯ , e q n Ω ( e p i , e p j ) = Ω ( e p i , e q j ) = Ω ( e q i , e q j ) = 0 , ∀ i , j = 1 , ⋯ , n Ω ( e p i , e q i ) = 1 , ∀ i = 1 , ⋯ , n
每一个 2 n e e
所有同维数的辛空间均与标准辛空间 ( R 2 n , Ω )
辛空间 R 2 n S : R 2 n → R 2 n Ω ( S ξ , S η ) = Ω ( ξ , η ) , ∀ ξ , η ∈ R 2 n R 2 n Sp ( n , R )
线性变换 S : R 2 n → R 2 n
证明. 基向量的线性组合之斜数量积可以用基向量的斜数量积来表示. 若此变换不改变基向量的斜数量积, 则亦不改变任何向量的斜数量积.
称满足 A T J A = J 2 n A
辛矩阵 A p ( λ ) = det ( A − λ I ) p ( λ ) = λ 2 n p ( λ 1 )
证明. A = J − 1 A T − 1 J , 故
p ( λ ) = det ( J − 1 A T − 1 J − λ I ) = det ( A T − 1 − λ I ) = det ( A − 1 − λ I ) = det ( I − λ A ) = λ 2 n det ( λ 1 I − A ) = λ 2 n p ( λ 1 ) . 若 λ A λ 1
习题. 设 ( Z , Ω ) V ⊂ Z V Ω = { z ∈ Z ∣ Ω ( z , v ) = 0 , ∀ v ∈ V } , V
(1) V ⊂ W ⇒ W Ω ⊂ V Ω Z / V Ω V ∗ dim V + dim V Ω = dim Z V ΩΩ = V V Ω V × V V Ω Z = V ⊕ V Ω
证明. (1) 显然.
(2)
Ω ♭ : Z → V ∗ , z ↦ Ω ( z , ⋅ ) ,
ker Ω ♭ = V Ω .
(3)
dim Z − dim V Ω = dim V ∗ = dim V .
(4)
V ⊂ { z ∈ Z ∣ Ω ( z , v ) = 0 , ∀ v ∈ V Ω } = V ΩΩ , 且
dim V = dim V − dim V Ω = dim V ΩΩ .
(5)
V 是辛的说明
V ∩ V Ω = 0 , 由 (3) 有
Z = V ⊕ V Ω .
设对
v ~ ∈ V Ω 成立
Ω ( v ~ , V Ω ) = 0 , 又
Ω ( v ~ , V ) = 0 , 那么
Ω ( v ~ , Z ) = 0 , 故
v ~ = 0 .
哈密顿方程 设 ( Z , Ω ) Z X : Z → Z ∀ z ∈ Z H ∈ C 1 ( Z ) Ω ♭ ( X ( z )) = d H ( z ) Ω ( X ( z ) , v ) = d H ( z ) ( v ) , ∀ v ∈ Z
若 H H X ( z ) X H ( z ) H
称 z ˙ = X H ( z )
这是梯度在辛流形上的类比: H ∇ H Y ⟨ ∇ H , Y ⟩ = Y H ∇ H H X H Y Ω ( X H , Y ) = Y H X H
若 Z Ω ♭ : Z → Z ∗ , z ↦ d H ( z )
函数的拉回 函数的推进 向量场的推进 向量场的拉回 φ ∗ f = f ∘ φ . φ ∗ g = g ∘ φ − 1 . φ ∗ X ( φ ( z )) = D φ ( z ) ⋅ X ( z ) . φ ∗ Y = ( φ − 1 ) ∗ Y .
典则变换或辛变换 设 ( Z , Ω ) , ( Y , Ξ ) f : Z → Y f Ξ ( D f ( z ) ⋅ z 1 , D f ( z ) ⋅ z 2 ) = Ω ( z 1 , z 2 ) z ∈ Z , z 1 , z 2 ∈ Z f ∗ Ξ = Ω
设 f q q = ( q 1 , ⋯ , q n ) φ : ( R 2 n , J ) → ( R 2 n , J ) φ ( q , p ) = ( q , p + df ( q )) = ( q 1 , ⋯ , q n , p 1 + ∂ q 1 ∂ f , ⋯ , p n + ∂ q n ∂ f ) . φ D : = D φ = [ I f qp I ] D T J D = J
设 ( Z , Ω ) H ∈ C 1 ( Z ) H ( z ) − H ( 0 ) = ∫ 0 1 Ω ( X H ( t z ) , z ) d t .
证明. H ( z ) − H ( 0 ) = ∫ 0 1 d t d H ( t z ) d t = ∫ 0 1 d H ( t z ) ⋅ z d t = ∫ 0 1 Ω ( X H ( t z ) , z ) d t . □
设 ( Z , Ω ) , ( Y , Ξ ) f : Z → Y f Y X H f ∗ X H ∘ f = X H D f ( z ) ⋅ X H ∘ f ( z ) = X H ( f ( z ))
证明. 当
f 是辛的,
Ξ ( D f ( z ) ⋅ X H ∘ f ( z ) , D f ( z ) ⋅ u ) = Ω ( X H ∘ f ( z ) , u ) = d ( H ∘ f ) ( z ) ⋅ u = d H ( f ( z )) ⋅ f ∗ ( z ) ⋅ u = Ξ ( X H ( f ( z )) , f ∗ ( z ) ⋅ u ) . 反过来, 有
Ξ ( D f ( z ) ⋅ X H ∘ f ( z ) , D f ( z ) ⋅ u ) = Ω ( X H ∘ f ( z ) , u ) , 恰当地选择哈密顿函数
H ,
X H ∘ f ( z ) 能取到任一
z ∈ Z , 因而
f 是辛的.
习题. 设 R 2 n Ω [ B − I I 0 ] , B = [ B ij ] n × n I Ω R 2 n Ω d t d q i = ∂ p i ∂ H , d t d p i = − ∂ q i ∂ H − B ij ∂ p j ∂ H .
证明. 设 z ( t ) = ( q i ( t ) , p i ( t )) [ B − I I 0 ] [ − B I − I 0 ] = [ I 0 0 I ] , d t d z = X H ( z ) = ∇ H ⋅ [ − B I − I 0 ] , ( d t d q i , d t d p i ) = ( ∂ q i ∂ H , ∂ p i ∂ H ) [ − B I − I 0 ] = ( ∂ p i ∂ H , − ∂ q i ∂ H − B ij ∂ p j ∂ H ) . □
设 ( R 2 n , J ) 2 n ( q i , p i ) X H : Z → Z X H = J ⋅ ∇ H ( d t d q i , d t d p i ) = ( ∂ p i ∂ H , − ∂ q i ∂ H ) .
设 c ( t ) X H H ( c ( t )) φ t X H φ t z ˙ = X H ( z ) z ( 0 ) = z ∈ Z H ∘ φ t = H
证明. d t d H ( c ( t )) = d H ( c ( t )) ⋅ c ˙ ( t ) = Ω ( H ( c ( t )) , c ˙ ( t )) = Ω ( H ( c ( t )) , H ( c ( t ))) = 0. 从而
H ( c ( t )) = H ( c ( 0 )) , 即
H ∘ φ t ( z ) = H ( z ) .
方程何时是哈密顿的 X : Z → Z ( Z , Ω ) X = X H H : Z → R ∀ z D X ( z ) Ω
证明. 设
X = X H , 在
u 方向上, 关于
z 对
Ω ( X H ( z ) , v ) = d H ( z ) ⋅ v 微分, 得到
Ω ( D X H ( z ) ⋅ u , v ) = D 2 H ( z ) ( v , u ) . 用二阶偏导数的对称性, 得到
Ω ( D X H ( z ) ⋅ u , v ) = D 2 H ( z ) ( u , v ) = Ω ( D X H ( z ) ⋅ v , u ) = − Ω ( u , D X H ( z ) ⋅ v ) . 反过来, 设
Ω ( D X H ( z ) ⋅ u , v ) = − Ω ( u , D X H ( z ) ⋅ v ) , 定义
H ( z ) = ∫ 0 1 Ω ( X ( t z ) , z ) d t , 则有
X = X H , 这是因为
Ω ( X H ( z ) , u ) = d H ( z ) ⋅ u = ∫ 0 1 Ω ( D X ( t z ) ⋅ t u , z ) d t + ∫ 0 1 Ω ( X ( t z ) , u ) d t = − ∫ 0 1 Ω ( t u , D X ( t z ) ⋅ z ) d t + ∫ 0 1 Ω ( X ( t z ) , u ) d t = ∫ 0 1 Ω ( t D X ( t z ) ⋅ z , u ) d t + ∫ 0 1 Ω ( X ( t z ) , u ) d t = ∫ 0 1 Ω ( t D X ( t z ) ⋅ z + X ( t z ) , u ) d t = ∫ 0 1 Ω ( d t d ( X ( t z ) t ) , u ) d t = Ω ( X ( z ) , u ) . 设 X ( z ) = A z A Ω ( A u , v ) = − Ω ( u , A v ) u , v ∈ Z H = ∫ 0 1 Ω ( t A z , z ) d t = 2 1 Ω ( A z , z ) .
习题. 设 ( Z , Ω ) A : Z → Z I − A A ( I + A ) ( I − A ) − 1 I − A
证明. ⇔ ⇔ ⇔ Ω (( I + A ) ( I − A ) − 1 z 1 , ( I + A ) ( I − A ) − 1 z 2 ) = Ω ( z 1 , z 2 ) Ω (( I + A ) z 1 , ( I + A ) z 2 ) = Ω (( I − A ) z 1 , ( I − A ) z 2 ) Ω ( A z 1 , z 2 ) + Ω ( z 1 , A z 2 ) = Ω ( − A z 1 , z 2 ) + Ω ( z 1 , − A z 2 ) Ω ( A z 1 , z 2 ) = − Ω ( z 1 , A z 2 ) . ( R 2 n , J ) A = ( I n 0 0 − I n )
例子 ii. 令
Z 是一个无限维 Hilbert 空间,
A = i T ,
T 是
Z 上的对称而不自伴的算子 (具体例子见 [
ZG ] 例 6.1.6, 6.1.7 等) , 则
I − A 不映满整个
Z (见 [
ZG ] 定理 6.2.4) .
习题. 设 ( Z , Ω ) φ : Z → Z det φ = 1 λ k 1/ λ φ
证明. 设 φ p ( x ) = ( x − λ ) k q ( x ) p ( x ) = x 2 n p ( x 1 ) = x 2 n ( x 1 − λ ) k q ( x 1 ) = ( 1 − λ x ) k x 2 n − k q ( x 1 ) . □
哈密顿流 考察辛向量空间 ( Z , Ω ) X H H : Z → R φ t : Z → Z d t d φ t ( z ) = X H ∘ φ t ( z ) , ∀ z ∈ Z , t ∈ R .
哈密顿向量场 X H φ t X
证明. 对哈密顿向量场
X H 的流
φ t , 用命题
3.29 ,
d t d Ω ( D φ t ( z ) ⋅ u , D φ t ( z ) ⋅ v ) = Ω ( D ( d t d φ t ( z ) ) ⋅ u , D φ t ( z ) ⋅ v ) + Ω ( D φ t ( z ) ⋅ u , D ( d t d φ t ( z ) ) ⋅ v ) = Ω ( D ( X H ∘ φ t ( z )) ⋅ u , D φ t ( z ) ⋅ v ) + Ω ( D φ t ( z ) ⋅ u , D ( X H ∘ φ t ( z )) ⋅ v ) = Ω ( D X H ( φ t ( z )) ⋅ D φ t ( z ) ⋅ u , D φ t ( z ) ⋅ v ) + Ω ( D φ t ( z ) ⋅ u , D X H ( φ t ( z )) ⋅ D φ t ( z ) ⋅ v ) = 0. 反之,
φ t ∗ Ω = Ω 说明
0 = d t d Ω ( D φ t ( z ) ⋅ u , D φ t ( z ) ⋅ v ) = Ω ( D X ( φ t ( z )) ⋅ D φ t ( z ) ⋅ u , D φ t ( z ) ⋅ v ) + Ω ( D φ t ( z )) ⋅ u , D ( X ( φ t ( z )) ⋅ D φ t ( z ) ⋅ v ) . 取
t = 0 ,
D φ 0 = I , 就有
0 = Ω ( D X ( z ) ⋅ u , v ) + Ω ( u , D X ( z ) ⋅ v ) , 由命题
3.29 可知
X 是哈密顿的.
在哈密顿系统标准理论中, 我们经常构造一个函数 F ( p , q ) F ( p , q ) X F 1 X F 1
泊松括号 设 ( Z , Ω ) F , G : Z → R 泊松括号 { F , G } : Z → R { F , G } ( z ) = Ω ( X F ( z ) , X G ( z )) . Lie 导数 L X f = df ⋅ X L X f = ( j = 1 ∑ n ∂ z j ∂ f d z j ) ( j = 1 ∑ n X j ∂ z j ) = j = 1 ∑ n ∂ z j ∂ f X j .
这样
{ F , G } ( z ) = Ω ( X F ( z ) , X G ( z )) = d F ( z ) ⋅ X G ( z ) = L X G F ( z ) = − Ω ( X G ( z ) , X F ( z )) = d G ( z ) ⋅ X F ( z ) = − L X F G ( z ) . 设 Z 2 n q i , p i { F , G } = Ω ( X F , X G ) = Ω ( ( ∂ p i ∂ F , − ∂ q i ∂ F ) , ( ∂ p i ∂ G , − ∂ q i ∂ G ) ) = i = 1 ∑ n ∂ q i ∂ F ∂ p i ∂ G − ∂ p i ∂ F ∂ q i ∂ G . { q i , q j } = 0 , { p i , p j } = 0 , { q i , p j } = k = 1 ∑ n ∂ q k ∂ q i ∂ p k ∂ p j − ∂ p k ∂ q i ∂ q k ∂ p j = δ j i .
两个函数 F , G : Z → R 对合的 或泊松可交换 的, 若 { F , G } = 0
给定 R n X , Y φ X t φ Y s = φ Y s φ X t t , s ∈ R
R 2 X = ∂ x ∂ , Y = x ∂ y ∂ X = ∂ x ∂ Y = x ∂ y ∂ ⇒ { x ˙ = 1 y ˙ = 0 ⇒ { x ( t ) = t + x 0 y ( t ) = y 0 , ⇒ { x ˙ = 0 y ˙ = x ⇒ { x ( t ) = x 0 y ( t ) = x 0 t + y 0 . φ X t φ Y s ( x 0 , y 0 ) φ Y s φ X t ( x 0 , y 0 ) = φ X t ( x 0 , x 0 s + y 0 ) = ( t + x 0 , x 0 s + y 0 ) , = φ Y s ( t + x 0 , y 0 ) = ( t + x 0 , t s + x 0 s + y 0 ) . t s = 0 φ X t φ Y s ( x 0 , y 0 ) = φ Y s φ X t ( x 0 , y 0 ) .
为了刻画 X , Y φ X t , φ Y s [ X , Y ]
两个向量场 X , Y Jacobi–Lie 括号 [ X , Y ] f ∈ C ∞ ( Z ) df [ X , Y ] = d ( df ⋅ Y ) ⋅ X − d ( df ⋅ X ) ⋅ Y , L [ X , Y ] f = L X L Y f − L Y L X f .
[ X , Y ] j = X i ∂ z i ∂ Y j − Y i ∂ z i ∂ X j = X Y j − Y X j .
证明. 后一等号就是
X = X i ∂ z i ∂ , Y = Y i ∂ z i ∂ . 前一等号是因为
[ X , Y ] f = X i ∂ z i ∂ ( Y j ∂ z j ∂ f ) − Y j ∂ z j ∂ ( X i ∂ z i ∂ f ) = X i ∂ z i ∂ Y j ∂ z j ∂ f + X i Y j ∂ z i ∂ z j ∂ 2 f − Y j ∂ z j ∂ X i ∂ z i ∂ f − Y j X i ∂ z j ∂ z i ∂ 2 f = X i ∂ z i ∂ Y j ∂ z j ∂ f − Y j ∂ z j ∂ X i ∂ z i ∂ f . 注: 这就是说
[ X , Y ] = ( X Y j − Y X j ) ∂ z j ∂ .
R 2 X = ∂ x ∂ , Y = x ∂ y ∂ [ X , Y ] = ( X ( 0 ) − Y ( 1 ) ) ∂ x ∂ + ( X ( x ) − Y ( 0 ) ) ∂ y ∂ = ∂ y ∂ .
[ X F , X G ] ( z ) = d X G ( z ) ⋅ X F ( z ) − d X F ( z ) ⋅ X G ( z ) .
证明. ∀ f ∈ C ∞ ( Z ) ,
L [ X F , X G ] f = L X F L X G f − L X G L X F f = L X F ( df ⋅ X G ) − L X G ( df ⋅ X F ) = d ( df ⋅ X G ) ⋅ X F − d ( df ⋅ X F ) ⋅ X G = d 2 f ⋅ X G ⋅ X F + df ⋅ ( d X G ⋅ X F ) − d 2 f ⋅ X F ⋅ X G − df ⋅ ( d X F ⋅ X G ) = df ⋅ ( d X G ⋅ X F − d X F ⋅ X G ) = L d X G ⋅ X F − d X F ⋅ X G f . 证明. Ω ( X { F , G } , v ) = d { F , G } ⋅ v = d ( Ω ( X F , X G )) ⋅ v = Ω ( d X F ⋅ v , X G ) + Ω ( X F , d X G ⋅ v ) = Ω ( d X F ⋅ X G , v ) − Ω ( d X G ⋅ X F , v ) = Ω ( − [ X F , X G ] , v ) .
Lie 代数 一个 Lie 代数 L [ − , − ] : L × L → L Jacobi 恒等式 [[ A , B ] , C ] + [[ B , C ] , A ] + [[ C , A ] , B ] = 0.
泊松括号 { − , − } : C ∞ ( Z ) × C ∞ ( Z ) → C ∞ ( Z ) C ∞ ( Z )
证明. 由于
{ F , G } = Ω ( X F , X G ) = d F ⋅ X G = X G ( F ) , 得
{ H , { F , G }} = − X { F , G } H = [ X F , X G ] H = X F X G H − X G X F H = X F { G , H } − X G { F , H } = { F , { G , H }} − { G , { F , H }} = { F , { G , H }} + { G , { H , F }} . 设 ( Z , Ω ) Z X Ham ( Z ) X ( Z )
证明. 对
X F , X G ∈ X Ham ( Z ) ,
[ X F , X G ] = − X { F , G } = X { G , F } ∈ X Ham ( Z ) .
设 X H Z φ t F ∈ C ∞ ( Z ) d t d ( F ∘ φ t ) = { F ∘ φ t , H } = { F , H } ∘ φ t .
证明. d t d ( F ∘ φ t ) = d F ⋅ d t d φ t = d F ⋅ X H ∘ φ t = { F , H } ∘ φ t . { F , H } ∘ φ t = φ t ∗ { F , H } = { φ t ∗ F , φ t ∗ H } = { F ∘ φ t , H ∘ φ t } = { F ∘ φ t , H } . □
设 F , G ∈ C ∞ ( Z ) F X G G X F { F , G } = 0
证明. d t d ( F ∘ φ t G ) = 0 ⇔ { F , G } ∘ φ t = 0 ⇔ { F , G } = 0. □
设 ( Z , Ω ) 2 n Z H F F X H
证明. 即
d t d ( H ∘ φ t F ) = 0 推出
d t d ( F ∘ φ t H ) = 0 , 事实上两者皆是
{ F , H } = 0 .
具有哈密顿函数 H F 1 , F 2
证明. 现有
{ F 1 , H } = 0 , { F 2 , H } = 0 , 由 Jacobi 恒等式,
{{ F 1 , F 2 } , H } = 0 .
习题. 验证 φ ∗ ( L X f ) = L φ ∗ X ( φ ∗ f )
证明. L φ ∗ X ( φ ∗ f ) ( z ) = L φ ∗ − 1 X f ∘ φ ( z ) = d ( f ∘ φ ) ⋅ ( φ ∗ − 1 X ) ( z ) = df ( φ ( z )) ⋅ D φ ( z ) ⋅ D φ − 1 ( φ ( z )) ⋅ X ( φ ( z )) = df ( φ ( z )) ⋅ X ( φ ( z )) = df ( X ) ( φ ( z )) = ( L X f ) ∘ φ ( z ) = φ ∗ ( L X f ) ( z ) . 附: 重点概念英文及示例 mechanics (力学) classical mechanics, Lagrangian mechanics, Hamiltonian mechanics motion (运动) equation of motion velocity (速度) relative velocity, angular velocity acceleration (加速度) centripetal acceleration, acceleration due to gravity momentum (动量) angular momentum, generalized momentum force (力) external force, frictional force, Coriolis force, Lorentz force moment (矩) moment of force energy (能量) potential energy, kinetic energy, total energy conservation (守恒) conservation law, conservation of momentum, conservation of energy
参考文献 [Li]
李书民. 经典力学概论. 中国科学技术大学出版社, 2007.
[Zh]
张恭庆. 变分学讲义. 现代数学基础. 高等教育出版社, 2001.
[Ar]
В. И. Arnold. 经典力学的数学方法. 俄罗斯数学教材选译. 高等教育出版社, 2006.
[SS]
E. M. Stein, R. Shakarchi. Fourier Analysis: An Introduction . Princeton Lectures in Analysis I. Princeton University Press, 2001.
[Fu]
H. Furstenberg. Recurrence in Ergodic Theory and Combinatorial Number Theory . Princeton University Press, 1981.
[MR]
J. E. Marsden, T. S. Raitu. 力学和对称性导论——经典力学系统初探. 应用数学译丛. 清华大学出版社, 1999.
[ZG]
张恭庆, 郭懋正. 泛函分析讲义 (下册) . 大学基础课教材. 北京大学出版社, 2001.