Hom 函子和单纯上同调
我们考虑 Abel 群之间的群同态:
设 A,G 都是 Abel 群, 记 A 到 G 的群同态全体是 Hom(A,G). G 上的加法结构可以诱导 Hom(A,G) 上的加法结构如下: (f+g)(a):=f(a)+g(a).于是 (Hom(A,G),+) 构成一个 Abel 群. 此时, 群同态 h:A→B 可以如下诱导一个 Hom(B,G) 到 Hom(A,G) 的同态: φh:A⟶hB⟶φG∈Hom(A,G),那么 h~:=Hom(h,G)=[φ↦φh] 是一个同态.
Hom:A↦Hom(A,G), h↦h~ 给出了一个从 Ab 到 Ab 的反变函子.
证明. 对
id:A→A,
id=Hom(id,G) 自然是
Hom(A,G) 上的恒等映射. 而对
A→hB→kC, 只需计算验证
kh(φ)=φkh=k~φh=h~k~φ可知
kh=h~k~, 也即
Hom 是一个反变函子.
设 h 是一个 Abel 群同态, 那么
1. | h 是同构 ⟹ h~ 是同构; |
2. | h=0⟹h~=0; |
3. | h 是满同态 ⟹h~ 是单同态; |
4. | 若序列正合且分裂, 则序列也正合且分裂. 也即 f 是单同态推 f~ 是满同态需要添加序列分裂的条件. |
证明. (1), (2) 的证明是容易的.
(3) 任取 φ∈Hom(B,G) 使得 h~(φ)=φh=0, 那么对任意 a∈A 成立h~(φ(a))=φh(a)=0,因 h 是满同态, 这即对任意 b∈B 有 φ(b)=0, 故 φ=0, 这说明 h~ 是单的.
(4) 只需证明在 Hom(B,G) 处正合, 也即 img~=kerf~.
因第一个序列正合, 故 fg=0, 由 (2) 可知 gf=f~g~=0. 于是 img~⩽kerf~. 再取 φ∈kerf~⩽Hom(B,G), 由 f~(φ)=φf=0 可知 imf⩽kerφ, 那么φ′:B/imf→G是由 φ 诱导的群同态, 满足因为 B→C 是满同态, 于是 g′ 是同构, 那么由交换图的可交换性得到φ=φ′(g′)−1g=g~(φ′(g′)−1)∈img~,于是 kerf~⩽img~.
再考虑另一部分的证明. 因第一个序列分裂, 于是存在
π:B→A 使得
πf=idA, 那么
πf=idA, 也即
f~π~=idA, 故
f~ 满,
π~ 单, 并且第二个序列也是分裂的.
在 (4) 中如果去掉序列分裂的条件, 那么结论往往不成立. 考虑 h:Z⟶×2Z, 这是一个单同态, 那么 h~:Hom(Z,Z)⟶2~Hom(Z,Z), 对 φ:Z→Z 是一个同态, 就有2~φ=φ(×2)=2φ,而 Hom(Z,Z)≅Z, 容易看出 h~ 并不是满同态.
设 A,G,Ai,Gi 是 Abel 群, 则
1. | Hom(i∈α⨁Ai,G)≅i∈α∏Hom(Ai,G); |
2. | Hom(A,i∈α∏Gi)≅i∈α∏Hom(A,Gi). |
证明. (1) 对 f:i∈α⨁Ai→G, 取 fi=f∣Ai, 那么 Φ:f↦i∈α∏fi 就是一个 Hom(i∈α⨁Ai,G)→i∈α∏Hom(Ai,G) 的同态.
反之, 对 f=i∈α∏fi, fi:Ai→G, 定义 Ψ(f):i∈α⨁Ai→G 满足 Ψ(f)(a)=i∈α∑fi(ai) 即可. 这里限制到代数直和是因为有限和的限制让我们无需考虑级数.
设 G 是 Abel 群, 则Hom(Z,G)≅G,Hom(Z/mZ,G)≅ker[G⟶mG].
证明. 第一个断言取
λ:Hom(Z,G)→G,φ↦φ(1)就是一个同构. 而对第二个断言, 由于序列
正合, 那么
也是正合的. 这里
φ~ 是单同态导出了
Hom(Z/mZ,G)≅imφ, 而序列正合导出了
imφ~≅kerm~.
在单纯同调理论中, 我们通过单纯链复形 C 导出了单纯同调群 Hp(C). 那么 Hom 函子作用之后的 Hom(C;G), 我们希望它也对偶地导出同调群.
对单纯复形 K, 考虑如下导出的链群:称 Hom(Cp(K),G):=Cp(K;G) 是 p 维上链群, 这里的 δ=Hom(∂,G).
Hom(C(K),G) 仍是一个链复形, 它以 δ=Hom(∂,G) 为边缘算子.
证明. 考虑δ:Cp(K;G)→Cp+1(K;G),cp↦δcp=∂~cp=cpδ,这里 δcp:Cp+1(K)→Cp(K). 并且δcp(cp+1)=cp(∂cp+1)可以看作是 cp 作用于 cp+1 上的值, 于是我们把它写成类似于内积的形式: ⟨δcp,cp+1⟩=⟨cp,∂cp+1⟩.
于是可以在 Hom(C(K),G) 上定义上同调. 记kerδp:=Zp(K;G),imδp+1:=Bp(K;G),称Hp(K;G)=Zp(K;G)/Bp(K;G)是 K 的 p 维上同调群. (这里称作上同调完全是因为此时习惯把指标写在右上角, cohomology 的 co–前缀表示代数对偶).
对任何 Abel 群 G, 它有自由部分 (以 Z 为直和项) 和挠部分 (以 Z/mZ 为直和项), 而之前已经讨论过Hom(Z,G)≅G,Hom(Z/mZ,G)≅ker[G→mG].
我们需要注意, 由Cp(K;G)≅Hom(Cp(K),G)≅Hom(σ∈Sp+(K)⨁Z⟨σ⟩,G)≅σ∈Sp+(K)∏Hom(Z⟨σ⟩,G)未必是一个自由 Abel 群.
要计算 Hp(K;G), 就归结到计算 δc 的问题, 所以下面处理上链如何表达. 在单纯同调理论中, 有 p 维基本链 σα∈Sp+(K), 类似地, 我们希望也有 p 维基本上链.
先考虑 G=Z 的情形, 此时对 σβ∈Sp+(K), 定义⟨σα∗,σβ⟩:={1,0,β=αβ=α那么对任何 cp∈Cp(K;Z)=:Cp(K), 就有 cp=α∑nασα∗ (这里的和未必是有限和). 对一般的 Abel 群 G, 我们考虑 gασα∗, 这里 gα∈G. 之前把它写成内积的形式, 我们同样希望这里的 “内积” 保持双线性, 于是可以定义⟨gασα∗,σβ⟩:={gα,0,β=αβ=α那么对任何 cp∈Cp(K;Z)=:Cp(K), 就有 cp=α∑gασα∗ (同样地, 这里的和未必是有限和).
对 cp=α∑gασα∗, 有 δcp=α∑gαδσα∗.
证明. 对
τ∈Sp+1+(K), 有
δτ=i=0∑p+1εiσi, 其中
εi=±1, 取决于
σi 的定向. (
这因低维单形的定向未必总是与高维单形定向相同.) 此时
⟨δcp,τ⟩=⟨α∑gασα∗,i=0∑p+1εiσi⟩=α∑i=0∑p+1gαεi⟨σα∗,σi⟩=i=0∑p+1εigi.而
⟨α∑gαδσα∗,τ⟩=i=0∑p+1εigi.这说明在每一个单形
τ 上
cp=α∑gασα∗, 于是命题得证.
由这一条件, 在几何上, δσα∗ 的计算可以简单地遵从下面的规则. 记 τi 是所有以 σα 为面的单形, 则δσα∗=i∑εiτi∗,这里 εi 是 σα 在 ∂τi 中的系数.
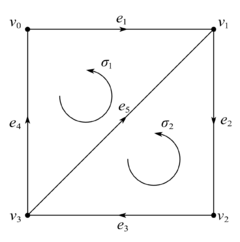
只需分别计算不同维数的基本上链的边缘即可. 对 2–基本上链δσ1∗=δσ2∗=0,对 1–基本上链, 有δe1∗=δe4∗=−σ1∗,δe2∗=δe3∗=−σ2∗,δe5∗=σ1∗−σ2∗.对 0–基本上链, 有δv0∗=e4∗−e1∗,δv1∗=e1∗−e2∗+e5∗,δv2∗=e2∗−e3∗,δv3∗=e3∗−e4∗−e5∗.
考虑 K 关于系数 Z 的上同调群: 列出 K 的上链复形有那么 imδ0=0 导出 H0(K)≅kerδ0=Z0(K), 对任意 c0=i=0∑3nivi∗∈C0(K), 由δc0=0⟺i=0∑3niδvi∗=0⟺(n0−n3)e4∗+(n1−n0)e1∗+(n2−n1)e2∗+(n3−n2)e3∗=0⟺n0=n1=n2=n3=n.这就说明 Z0(K)=Z⟨i=0∑3vi∗⟩≅Z, 于是 H0(K)≅Z.
再考虑 p=1 的情形, Z1(K)=kerδ1, 对 c1=i=1∑5niei∗∈C1(K), 类似地有δc1=0⟺{n1=n5−n4n2=−n3−n5.于是对 c1∈Z1(K), 有c1=(n5−n4)e1∗+(−n3−n5)e2∗+n3e3∗+n4e4∗+n5e5∗=n3(e3∗−e2∗)+n4(e4∗−e1∗)+n5(e1∗−e2∗+e5∗)=−n3δv2∗+n4δv0∗+n5δv1∗,这即 Z1(K)=B1(K), 于是 H1(K)=Z1(K)/B1(K)=0.
当 p=2 时, 因 kerδ2=C2(K), 故 H2(K)=C2(K)/imδ1=C2(K)/B2(K), 而σ1∗=−δe1∗,σ2∗=δe2∗说明 C2(K)=B2(K), 从而 H2(K)=0. 其他阶上同调群自然为零.
这样的计算无疑是低效而繁复的.
设 K 是单纯复形, 有H0(K;G)={c0∈C0(K):∀v,w位于∣K∣的同一连通分支,⟨c0,v⟩=⟨c0,w⟩}.特别地, 若 ∣K∣ 连通, 就有 H0(K;G)≅G.
证明. 设 c0 满足条件, 要证 δc0=0 当且仅当对任意 σ=[v,w]∈S1+(K) 都有 ⟨δc0,σ⟩=0.
因⟨δc0,σ⟩=⟨c0,∂σ⟩=⟨c0,w⟩−⟨c0,v⟩=0,于是 c0∈kerδ0=H0(K;G).
反之, 若 c0∈kerδ0, 即 δc0=0, 则当 v,w 位于 ∣K∣ 的同一连通分支时, 存在 c1∈C1(K) 使得 ∂c1=w−v, 那么0=⟨δc0,c1⟩=⟨c0,∂c1⟩=⟨c0,w⟩−⟨c0,v⟩,这即 ⟨c0,w⟩=⟨c0,v⟩.
当
∣K∣ 连通时, 对任何
v,w∈K(0), 应有
v,w 位于同一同调类中. 于是对任何
c0=v∈K(0)∑gvv∗∈kerδ0,
gv=⟨c0,v⟩=⟨c0,w⟩=gw,这即
c0=gv∈K(0)∑v∗, 从而
H0(K;G)≅G.
对上链复形做增广, 得到它导出的上同调群称作约化上同调群, 并且容易得到 H~p(K;G)≅Hp(K;G).
imε~⩽kerδ0, 进一步 H0(K;G)≅H~0(K;G)⊕G.
证明. 任取 α∈imε~, 即存在 φ∈Hom(Z,G) 使得 ε~(φ)=α, 那么δ0α=δ0ε~(φ)=ε∂1(φ)=0,即 α∈kerδ0, 从而 imε~⩽kerδ0. 那么kerδ0=imε~kerδ0⊕imε~.
那么这就是
H0(K;G)=kerδ0=imε~kerδ0⊕imε~=H~0(K;G)⊕Hom(Z;G)≅H~0(K;G)⊕G.特别地, 当
∣K∣ 连通时
H~0(K;G)=0.
对复形对 (K,K0), 有(K,K0)⟶C(K,K0)⟶Hom(C(K,K0),G),后者是一个链复形, 于是可以定义相对上同调群Hp(K,K0;G):=Zp(K,K0;G)/Bp(K,K0;G).
注意到 Cp(K,K0;G) 可以看作是 Cp(K;G) 的子群, 这因Cp(K,K0;G)E={f:Cp(K,K0)→G}≅{f:Cp(K)→G:f∣Cp(K0)=0}⩽Cp(K;G).并且 Cp(K0;G) 可以看作 Cp(K;G) 的商群, 考虑~:Cp(K;G)↠Cp(K0;G),φ↦~(φ)=φ∣Cp(K0)=φi:Cp(K0)→G.由同态基本定理可知Cp(K;G)/ker~≅Cp(K0;G).
在同调理论中有正合且分裂的序列于是由 5.1.3 可知序列仍然正合且分裂. 于是 zig–zag 引理导出长正合序列
考虑 5.1.8 中相同的复形 K, K0 是由 {vi}i=14 和 {ei}i=14 构成的子复形.
注意到 K0 是 1 维子复形, 于是 H2(K0)=0. 由 5.1.8 我们已经得到 H1(K)=H2(K)=0, 于是长正合列导出 H2(K,K0)≅H1(K0), 而 H1(K0) 是容易计算的.
由 dimK0=1 可知 Z1(K0)=C1(K0). 此时 e1∗∼e2∗∼e3∗∼e4∗, 于是 C1(K0)≅Z⟨e1∗⟩. 而对任意 c0∈C0(K0) 和 z=i=1∑4ei∈Z1(K), 由⟨δc0,z⟩=⟨c0,∂z⟩=0和⟨ne1∗,z⟩=n⟨e1∗,e1⟩=n可知 B1(K0)=0. 从而 H1(K0)≅Z, 因此 H2(K,K0)≅Z.
对一般链复形 C={(Cp,∂)}, 这里 Cp 是 Abel 群, 它经过 Hom 函子之后得到的Hom(C,G)={(Hom(Cp,G),δ)}={(Cp(C;G),δ)}仍然是一个链复形, 于是同样地可以定义上同调群 Hp(C;G):=kerδp/imδp−1.
若 C 可以截断, 适当地调整下标, 在被截断的地方放上一个 Z 之后被 Hom 函子作用, 可以得到增广上链复形, 于是也可以诱导约化同调群.
考虑链映射 f:C→C′ 满足 ∂′f=f∂, 那么经过 Hom 函子作用之后得到的f~:Hom(C′;G)→Hom(C;G)满足∂′f=f∂⟹∂′f=f∂⟹f~δ′=δf~,它诱导 f∗:Hp(C′;G)→Hp(C;G).
同样地, 将链同伦的交换图表作 Hom 函子之后, 我们自然地得到上链同伦:它自然也满足 D~δ′−δD~=g~−f~. 并且同样满足同伦公理, 即 φ~≃ψ~⟹φ∗=ψ∗.
但对一般的链复形, 正合列未必是分裂的, 因为 C, D, E 未必是自由的. 因此无法推出序列的正合性.
所以我们取一个简单的例子, 考虑空间对 (X,A) 的奇异链复形自然是一个分裂的正合列, 因此它总是可以诱导长正合列并且映射 f:(X,A)→(Y,B) 诱导链映射 f♯:Hom(S(Y,B);G)→Hom(S(X,A);G). 这里 f♯ 如下定义: 对任何 a∈Sp(X,A), 有f♯(φ)(a)=⟨f♯φ,a⟩=⟨φ,f♯(a)⟩.
考虑下面的一组公理:
1. | id:X→X 诱导出的 id∗ 是恒等映射; |
2. | X→fY→gZ 导出 (gf)∗=f∗g∗; |
3. | δ∗ 是自然变换, 即对 f:(X,A)→(Y,B), 有图交换; |
4. | 设 (X,A) 是容许对, 有长正合列 |
5. | 同伦公理: 若 f≃g:X→Y, 则 f∗=g∗; |
6. | 切除公理: 对复形对 (X,A), 若 U⊂X, Uˉ⊂IntA, 且 (X∖U,A∖U) 仍是容许对, 则 Hp(X∖U,A∖U;G)≅Hp(X,A;G); |
7. | 维数公理: 对单点空间 pt, 有 H~p(pt;G)=0. |
称这组公理导出的同调理论为上同调理论. 区别于同调理论, 上同调公理中没有紧支撑公理.
自由链复形的上同调
考虑这样一个问题, 对 C,D 都是自由链复形, Hp(C)≅Hp(D) 能否推出 Hp(C;G)≅Hp(D;G)? 如果这一问题的答案是肯定的, 那么我们立刻可以导出对可三角剖分的拓扑空间, 它们的单纯上同调, 奇异上同调和胞腔上同调都是相同的.
设 C 是一个 Abel 群, 若 A,B 都是自由的, 称短正合序列是 C 的一个自由可解. 任何 Abel 群 C 都存在自由可解, 我们只需要考虑下面的序列: 即可, 它显然是正合的.
设 C,C′ 是 Abel 群, γ:C→C′ 是同态, 它们都有自由可解. 则存在群同态 α:A→A′, β:B→B′ 使得图交换.
证明. 先考虑
β 的存在性, 取
b 是
B 的基元, 因
ψ′ 是满射, 于是
β(b)=b′∈(ψ′)−1(γψ(b))总是可以定义的. 于是
β 可以被定义.
下面断言
β(imφ)⩽imφ′. 这因
b∈imφ=kerψ⟹ψ(b)=0⟹γψ(b)=0⟹ψ′β(b)=0⟹β(b)∈kerψ′=imφ′,于是
β 可以如下诱导
α=(φ′)−1φ:A→A′.
设 C 和 D 是自由链复形, γ:Hp(C)→Hp(D) 是群同态, 则存在链映射 φ:C→D 使得 φ∗=γ.
证明. 考虑由 5.2.2 可知存在对应的群同态 α, β 使得上图交换.
考虑 β:Zp(C)→Zp(D), 将 β 扩张成链映射, 因为序列正合且分裂, 于是 Cp≅Zp⊕Up. 其中 ∂∣Up:Up→≅Bp−1 是一个同胚. 于是可以定义 φ:Cp→Dp 满足φ∣Zp=β,φ∣Up=(∂′∣Up′)−1α∂∣Up.再证明 φ 是一个链映射, 只需图交换, 这因每一个方块都可以交换.
再验证
φ∗=γ. 直接计算, 对任何
{zp}∈Hp(C), 都有
φ∗({zp})={φ(zp)}={β(zp)}=l′β(zp)=γl(zp)=γ({zp}),故
φ∗=γ.
设 C, D, E 都是自由链复形, 序列正合, 若 Hp(C)≅Hp(D), 则 Hp(C;G)≅Hp(D;G).
证明. Zig–zag 引理可以诱导出长正合列, 而 φ∗ 是同构意味着对任意 p∈Z 成立 Hp(E)=0. 并且题设中的序列分裂, 因此也是分裂的正合列. 于是 φ∗ 是同构当且仅当对任何 p∈Z 成立 Hp(E;G)=0.
设 Bp 和 Zp 分别是 E={(Ep,∂)} 的边缘链群和闭链群, 则 Hp(E)=0 导出序列正合. 于是 Ep=Zp⊕Up, 其中 ∂∣Up:Up→≅Bp−1 是同胚. 又因为 Hp(E)=0, 于是 Zp=Bp. 作 Hom 函子如下: Hom(Ep,G)=Hom(Zp,G)⊕Hom(Up,G)≅Hom(Zp,G)⊕Hom(Bp−1,G).对下图断言 δ∣Up=0. 因对任意 f:Up→G∈Hom(Up,G) 都有δf=∂~f=f∂:Bp−1→G,由 ∂∣Bp+1=0 可知 δf=0, 故 δ∣Up=0.
立刻得到
imδp−1=Hom(Up,G)=kerδp,于是
Hp(E)=kerδp/imδp−1=0.
下面的定理是 5.2.4 的一般情形. 在证明的过程中使用到了一个拓扑背景的技术, 即映射锥. 考虑 h:X→Y, 它可以如下诱导一个黏合:π:(x,0)∼h(x),此时 π 将 X 嵌入到 Y′ 中, 而 Y 被同伦地映射到 Y′ 中, 此时图在同伦意义下交换. 也即 i≃jh.
设 C, D 是自由链复形, 若 Hp(C)≅Hp(D), 则 Hp(C;G)≅Hp(D;G).
证明. 设 φ:C→D 是链映射, 若存在一个自由链复形 D′ 使得在同伦意义下交换, 即 i≃jφ, D′/imi 与 D′/imj 都是自由的, 则可以导出 j♯ 是一个同构.
取 D′={(Dp′,∂)} 如下. Dp′=Cp⊕Dp⊕Cp−1,∂p′:⎩⎨⎧ (cp,0,0) ↦(∂cp,0,0) (0,dp,0) ↦(0,∂dp,0)(0,0,cp−1)↦(−cp−1,φ(cp−1),−∂cp−1)容易验证 ∂′∘∂′=0.
此时 i:C→D′ 和 j:D→D′ 都是嵌入, 并且 i∂C=∂′i, j∂D=∂′j 也是显然的, 于是D′/imi={(Dp⊕Cp−1,∂′′)}D′/imj={(Cp⊕Cp−1,∂′′′)}∂′′=∂′∣Dp⊕Cp−1∂′′′=∂′∣Cp⊕Cp−1自然是自由的. 下面我们验证 i≃jφ. 取 D:Cp→Dp+1′ 满足 cp↦(0,0,cp), 那么直接计算∂′D(cp)+D(∂cp)=(−cp,φ(cp),0)=jφ(cp)−i(cp),这说明 ∂′D+D∂=jφ−i, 也即 i≃jφ.
因 j 是单的, 此时有短正合列那么 j∗ 是同构当且仅当对任意 p∈Z 都有 Hp(D′/D)=0, 即证 Zp(D′/D)=Bp(D′/D). 任取 zp=(cp,cp−1)∈Zp(D′/D), 那么由∂(cp,cp−1)=0⟺(∂cp−cp−1,−∂cp−1)=0⟺∂cp=cp−1,∂cp−1=0.这说明任何 zp 都具有 (cp,∂cp) 的形式, 注意到 ∂(0,−cp)=(cp,∂cp) 即可. 于是我们证明了 j∗ 是同构.
令
γ:Hp(C)→Hp(D) 是同构, 则
∂φ:C→D 使得
φ∗=γ. 此时
和
都是自由链复形的短正合列. 因
j∗ 是同构, 由
5.2.4 可知
j∗ 也是同构. 另一方面, 因
i≃jφ, 从而
i∗=j∗φ∗ 也是同构. 再使用一次
5.2.4 可知
i∗ 也是同构. 因此由
i∗=φ∗j∗和
i∗,
j∗ 都是同构得到
φ∗ 也是同构, 此即
Hp(C;G)≅Hp(D;G).
至此, 对单纯复形 K, 我们得到了这样的一些概念: 因此一个自然的问题是, Hp(C;G) 与 Hom(Hp(C),G) 何时是同构的?
考虑映射Hom(Cp,G)×Cp→G,(cp,cp)↦⟨cp,cp⟩,它诱导出Hp(C;G)×Hp(C)→G,({αp},{βp})↦⟨αp,βp⟩.称作是 Kronecker 指数.
它是良定义的, 因对 αp=zp+δbp−1, βp=zp+∂bp+1, 有⟨αp,βp⟩=⟨zp+δbp−1,zp+∂bp+1⟩=⟨zp,zp⟩+⟨bp−1,∂zp⟩+⟨δzp,bp+1⟩+⟨bp−1,∂2bp+1⟩=⟨zp,zp⟩.
称映射κ:Hp(C;G)→Hom(Hp(C),G),αp↦⟨αp,⋅⟩:Hp(C)→G是 Kronecker 映射.
证明. 我们构造这样的一个 λ∗:Hom(Hp(C),G)→Hp(C;G), 使得 κλ∗=id. 对自由链复形 C, 序列正合, 且 Cp=Zp⊕Up, Up≅Bp−1. 将商映射扩张得到λ:Cp→Hp(C),λ∣Zp:zp↦{zp},λ∣Up:up↦0,视 E={(Hp(C),∂=0)} 为一个链复形, 那么图自然是交换的, λ 是一个链映射. 从而它可以诱导λ∗:Hp(C)→Hp(E)=Hp(C),{zp}↦{λ(zp)}={zp}.同样地, 它也可以诱导λ∗:Hom(Hp(C),G)=Hp(E;G)→Hp(C;G),但 λ∗ 未必是同构, 这因 E 未必自由.
下面证明
κλ∗=id, 任取
γ={zp}∈Hp(C),
α∈Hom(Hp(C),G). 直接计算
κλ∗(α)(γ)=⟨λ∗(α),γ⟩=⟨λ∗(α,zp)⟩=⟨α,λ(zp)⟩=⟨α,{zp}⟩=α({zp}),于是对任何
α 都有
κλ∗(α)=α, 这即
κλ∗=id.
设 C 是自由链复形, 若 Hp(C) 也自由, 则 κ 给出一个 Hp(C;G) 与 Hom(Hp(C),G) 之间的同构.
证明. 由
Hp(C) 自由且
λ∗=id 可知
λ∗ 是同构.
Ext 函子和万有系数公式
对于一般的情形, 序列(可视作链复形 C) 正合未必可以导出序列(可视作链复形 Hom(C,G)) 也正合. 为此, 我们可以选择在左侧添加一项, 得到序列(这里的 cokerφ~ 可以看作是 H2(Hom(C,G))), 这就是一个正合序列了.
设 A 是一个 Abel 群, 其自由可解为那么对 Abel 群 G, 定义Ext(A;G):=cokerφ~=Hom(R,G)/imφ~.
设 A, G, Ai, Gi 是 Abel 群, 则
1. | Ext(i∈α⨁Ai,G)≅i∈α∏Ext(Ai,G); |
2. | Ext(A,i∈α∏Gi)≅i∈α∏Ext(A,Gi). |
证明. (1) 我们记 Ai 对应的自由可解为那么 i∈α⨁Ai 的自由可解就是因此下面的两个序列都是正合的. 而 5.1.4 说明了序列中前三项可以与直积建立起自然的同构, 于是从交换图上可以得到 Ext(i∈α⨁Ai,G) 到 i∈α∏Ext(Ai,G) 的映射是一个同构.
(2) 类似地, 我们考虑下面的两个正合序列
同样地,
5.1.4 说明了序列前三项可以与直积建立起自然的同构, 于是从交换图上可以得到
Ext(A,i∈α∏Gi) 到
i∈α∏Ext(A,Gi) 的映射是一个同构.
下面的命题可以让我们很简单地计算有限生成 Abel 群的 Ext 函子. 它应用于通过万有系数公式计算上同调群的过程.
设 A,G 是 Abel 群, 则
1. | 若 A 是自由群, 则 Ext(A,G)=0; |
2. | 序列正合. |
3. | Ext(Z,G)=0, Ext(Z/mZ,G)≅G/mG. |
证明. (1) 注意到 A 是自由群时, A 的自由可解是分裂的, 于是经过 Hom 函子作用之后直接得到一个正合序列, 这就说明了 Ext(A,G)=0.
(2) 只需注意到 Z/mZ 有自由可解即可.
设 C 是自由链复形, G 是 Abel 群, 则序列正合.
证明. 注意到对任何 p∈Z, 序列和都正合, 并且由 Bp−1 自由可知下面的序列还是分裂的, 于是我们得到序列也是正合的, 其中 ∂ˉ 是 ∂ 的商映射. 我们把这一序列换一种写法, 得到下面证明它是分裂的.
注意到有交换图
其中所有竖直方向和水平方向的序列都是正合列, 因此上图导出
kerαp−1=ker∂ˉ∗=Zp−1⟹kerαp=Zp,和
kerβp−1=im∂ˉ∗=Bp.因此有
cokerβp−1=Zp/Bp=Hp(C;G). 注意到
βp−1=∂ˉ∗γp−1, 于是序列
这就是所求证的序列.
对 Klein 瓶 S, 我们已经得到它的同调群Hp(S)=⎩⎨⎧Z,Z⊕Z/2Z,0,p=0p=1其他那么利用万有系数公式, 当 p=1 时序列的正合性导出 H1(S;G)≅G⊕ker[G→2G].
特别地, 取 G=Z 有 H1(S;Z)≅Z; 取 G=Z/2Z 有 H1(S;Z/2Z)≅Z⊕Z/2Z.
当 p=2 时序列的正合性导出 H2(S;G)≅G/2G.