4. CW 复形的同调

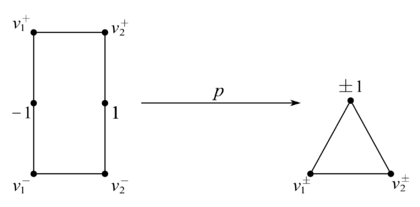
4.1CW 复形及其结构

与 ${\mathbb{D}}^n$ 同胚的几何体称作一个 $n$–胞腔 ($n$–cell), 与 ${\mathbb{B}}^n$ 同胚的几何体称作一个 $n$–开胞腔. 习惯上记 $n$–开胞腔为 $e_n$, $n$–胞腔为 ${\bar{e}}_n$. 特别地, 约定 $0$–胞腔是单点 $\mathrm{pt}$, 并用 $e_0$ 记它.

例 4.1.1. 球面 ${\mathbb{S}}^n$ 可以看作是一个 $0$–胞腔 $e_0$ 和一个 $n$–开胞腔 $e_n$ 构成的, 这因 ${\mathbb{S}}^n$ 去掉北极点 $N$ 后$${\mathbb{S}}^n\setminus N\cong {\mathbb{R}}^n\cong {\mathbb{B}}^n\cong e_n.$$那么多个球面的一点并从胞腔的角度来看是一件非常平凡的事情. $k$ 个不同维数的球面一点并 ${\mathbb{S}}^{n_1}\vee {\mathbb{S}}^{n_2}\vee \cdots \vee {\mathbb{S}}^{n_k}$ 无非就是 $e_0,e_{n_1},e_{n_2},\dots ,e_{n_k}$ 构成的.

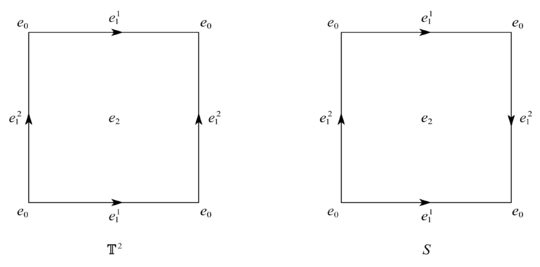
例 4.1.2 (环面和 Klein 瓶). 环面 ${\mathbb{T}}^2$ 和 Klein 瓶 $S$ 都可以看作一个 $0$–胞腔 $e_0$, 两个 $1$–开胞腔 $e_1^1$ 和 $e_1^2$, 以及一个 $2$–开胞腔 $e_2$ 构成的复形:

定义 4.1.3 (CW 复形). 称 $X$ 是一个 CW 复形, 若 $X$ 是一个拓扑空间, 一族不交的开胞腔 ${\left\{e_{\alpha }\right\}}_{\alpha \in \mathcal{A}}$ 使得 $X=\bigcup _{\alpha \in \mathcal{A}}{e}_{\alpha }$, 满足

1.	$X$ 是 Hausdorff 空间;
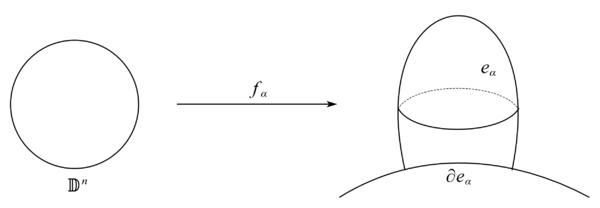
2.	对任何 $m$–开胞腔 $e_{\alpha }^m$, 存在其示性映射 $f_{\alpha }:{\mathbb{D}}^m\to X$ 使得 $f_{\alpha }:{\mathbb{B}}^m\to e_{\alpha }^m$ 是一个同胚, 且 $f_{\alpha }(\mathrm{Bd}{\mathbb{B}}^m)$ 落在有限多个维数低于 $m$ 的开胞腔的并中; (注意这里不需要边缘与开胞腔的并相等, 只需要落在其中即可.)
3.	对 $A\subset X$, 若对任意 $e_{\alpha }$ 都有 $A\cap {\bar{e}}_{\alpha }$ 是 ${\bar{e}}_{\alpha }$ 中的闭子集, 则 $A$ 是 $X$ 中的闭子集.(称作是 $X$ 上的弱拓扑).

特别地, 若 $\left|\mathcal{A}\right|<\infty$, 称 $X$ 是一个有限 CW 复形, 其维数可由 $\dim X=\underset{\alpha }{\max }\dim e_{\alpha }$ 定义. 此时 $X$ 是 $T_4$ 空间.

CW 复形中, C 意为 closure–finite, 闭有限性, 而 W 意为 weak topology, 即 3 中定义的拓扑.

命题 4.1.4. 设 $X$ 是一个 CW 复形, $e_{\alpha }$ 是其一个胞腔, $f_{\alpha }$ 是 $e_{\alpha }$ 的示性映射. 有 $f_{\alpha }({\mathbb{D}}^m)={\bar{e}}_{\alpha }$ 且 $f_{\alpha }(\mathrm{Bd}{\mathbb{B}}^m)=\partial {\bar{e}}_{\alpha }$.

证明. 由 $f_{\alpha }$ 的连续性可知$$f_{\alpha }({\mathbb{D}}^m)=f_{\alpha }({\bar{\mathbb{B}}}^m)\subset \overline{f_{\alpha }({\mathbb{B}}^m)}={\bar{e}}_{\alpha }.$$反之, 因 ${\mathbb{D}}^m$ 是紧的, 于是 $f_{\alpha }({\mathbb{D}}^m)$ 是 $X$ 中的紧集. 因 $X$ 是 $T_3$ 的, 有 $f_{\alpha }({\mathbb{D}}^m)$ 是闭集, 因此 ${\bar{e}}_{\alpha }\subset f_{\alpha }({\mathbb{D}}^m)$. 这就说明了 $f_{\alpha }({\mathbb{D}}^m)={\bar{e}}_{\alpha }$.

而$$\varnothing =f_{\alpha }({\mathbb{B}}^m)\cap f_{\alpha }(\mathrm{Bd}{\mathbb{B}}^m)=e_{\alpha }\cap f_{\alpha }(\mathrm{Bd}{\mathbb{B}}^m),$$于是$$f_{\alpha }(\mathrm{Bd}{\mathbb{B}}^m)={\bar{e}}_{\alpha }\setminus e_{\alpha }=\partial e_{\alpha }.$$命题得证.

$\square$

命题 4.1.5. 设 $X$ 是 CW 复形, 那么 $f:X\to Y$ 连续当且仅当 $f$ 限制到每一个开胞腔 $f{|}_{e_{\alpha }}$ 都连续.

证明. 必要性是显然的, 下面证明充分性. 任取 $B\subset Y$ 是一个闭集, 对任意的 $e_{\alpha }\subset X$, 因$$f^{-1}(B)\cap e_{\alpha }=(f{|}_{e_{\alpha }}{)}^{-1}(B)$$是 ${\bar{e}}_{\alpha }$ 中的闭子集, 于是 $f^{-1}(B)$ 是闭集.

$\square$

为了处理 CW 复形的同伦, 我们把上面的命题简单推广一下, 对 $X$ 做一次加厚:

推论 4.1.6. 设 $X$ 是 CW 复形, 那么 $f:X\times I\to Y$ 连续当且仅当对 $X$ 的每一个开胞腔 $e_{\alpha }$, $f{|}_{e_{\alpha }\times I}$ 是连续的.

定义 4.1.7 (CW 子复形). 设 $X$ 是一个 CW 复形, $Y\subset X$ 是一族 $X$ 中开胞腔的并, 且满足若 $e_{\alpha }\subset Y$, 则 ${\bar{e}}_{\alpha }\subset Y$. 则 $Y$ 也是一个 CW 复形, 称作是 $X$ 的 CW 子复形. 它是 $X$ 的闭集.

证明. 首先 $Y$ 作为 $X$ 的子空间是 Hausdorff 的, 且对于任意 $e_{\alpha }\subset Y\subset X$, 因 $X$ 是 CW 复形, 存在其示性映射 $f_{\alpha }:{\mathbb{D}}^m\to X$ 使得 $f_{\alpha }({\mathbb{D}}^m)={\bar{e}}_{\alpha }\subset Y$, 于是$$f_{\alpha }(\mathrm{Bd}{\mathbb{B}}^m)\cap {\left\{e_{\beta }\right\}}_{\beta \in I_{\alpha }}\subset Y,$$这里 $I_{\alpha }$ 是那些与 ${\bar{e}}_{\alpha }$ 有非空交的 $\beta$ 全体. 那么 $f_{\alpha }(\mathrm{Bd}{\mathbb{B}}^m)$ 落在 $Y$ 中有限多个开胞腔的并中. 这说明了闭有限性.

设 $B\subset Y$ 使得对任意 $e_{\alpha }\subset Y$ 都有 $B\cap {\bar{e}}_{\alpha }$ 在 ${\bar{e}}_{\alpha }$ 中闭, 我们需要证明它在 $Y$ 中也是闭集. 设 $e_{\beta }\subset X$ 但 $e_{\beta }\not\subset Y$, 则 $e_{\beta }\cap Y=\varnothing$, 进而 ${\bar{e}}_{\beta }\cap Y=\partial e_{\beta }$. 由定义可知 ${\bar{e}}_{\beta }\cap Y$ 落在有限多个 $Y$ 的开胞腔之并中, 不妨设$${\bar{e}}_{\beta }\cap Y\subset e_{i_1}\cup \cdots \cup e_{i_k},$$那么$$B\cap {\bar{e}}_{\beta }=((B\cap {\bar{e}}_{i_1})\cup \cdots \cup (B\cap {\bar{e}}_{i_k}))\cap {\bar{e}}_{\beta }.$$于是 $B\cap {\bar{e}}_{\beta }$ 在 ${\bar{e}}_{\beta }$ 中是闭集 (因后面的每一个 $B\cap {\bar{e}}_{i_j}$ 都是闭的), 于是 $B$ 是 $X$ 中的闭子集. 从而 $B\cap Y=B$ 在 $Y$ 中是闭子集. 由定义可知 $Y$ 是

$\square$

推论 4.1.8 (骨架). 记使得 $\dim e_{\alpha }=p$ 的 $\alpha$ 全体为 ${\mathcal{A}}_p$, 再记 ${\mathcal{A}}_{⩽p}=\bigcup _{k⩽p}{\mathcal{A}}_k$. 那么由 4.1.7 可知$$X^p:=\bigcup _{\alpha \in {\mathcal{A}}_{⩽p}}{e}_{\alpha }$$是 $X$ 的一个 CW 子复形, 满足 $\dim X^p=p$, 称作是 $X$ 的 $p$ 维骨架.

借助骨架的概念, CW 复形可以如此归纳地定义: 在此之前先定义拓扑空间的拓扑和:

定义 4.1.9 (拓扑和). 给定两个拓扑空间 $(X_1,{\tau }_1)$, $(X_2,{\tau }_2)$, 在它们的无交并 $X_1\bigsqcup X_2$ 上定义拓扑$$\tau =\left\{U\subset X_1\bigsqcup X_2:U\cap X_i\in {\tau }_i\right\},$$称如此构成的拓扑空间 $(X_1\bigsqcup X_2,\tau )$ 是 $X_1$ 和 $X_2$ 的拓扑和.

定义 4.1.10 (正则 CW 复形). 若在 CW 复形的定义中, 对每一个开胞腔 $e_{\alpha }$, $\partial e_{\alpha }$ 都恰是有限多个维数更低的开胞腔之并, 则称 $X$ 是一个正则 CW 复形.

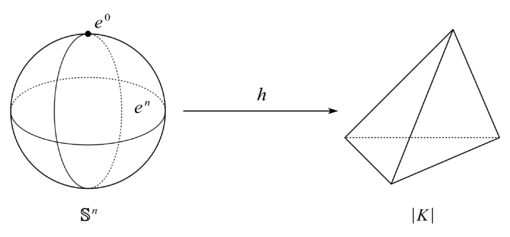
例 4.1.11. 设 $K$ 是一个单纯复形, 那么 $\left|K\right|=\bigcup _{\sigma \in K}\mathrm{Int}\sigma$ 是一个 CW 复形, 其开胞腔即为 ${\left\{\mathrm{Int}\sigma \right\}}_{\sigma \in K}$. 特别地, 它还是一个正则 CW 复形. 设另有 $\left|L\right|=\bigcup _{\tau \in L}\mathrm{Int}\tau$ 也是 CW 复形, 则$$\left|K\right|\times \left|L\right|=\bigcup _{\sigma \in K}\bigcup _{\tau \in L}(\mathrm{Int}\sigma \times \mathrm{Int}\tau )=\bigcup _{\sigma \in K}\bigcup _{\tau \in L}\mathrm{Int}(\sigma \times \tau )$$仍是一个 CW 复形, 且它是一个正则 CW 复形.

单纯复形对应的空间总是可以三角剖分的, 我们自然地可以去考虑 CW 复形的三角剖分. 仍然希望一些比较好的 CW 复形可以和单纯复形扯上那么一点儿关系.

定义 4.1.12 (三角剖分). 称 $K$ 是一个可三角剖分的 CW 复形, 若存在同胚 $h:X\to \left|K\right|$ 满足对任意 $p\in \mathbb{Z}$, 存在 $K$ 的子复形 $L$, $\dim L⩽p$ 使得 $h{|}_{X^p}:X^p\to \left|L\right|$ 是同胚.

需要注意的是, 单纯复形与 CW 复形本身是有一些区别的. 对 $n$ 维单纯复形 $K$, 总有$$K^{(0)}⫋K^{(1)}⫋\cdots ⫋K^{(n)}=K,$$其中的每一项与前一项的差都是非零的, 每一个包含关系都是严格的. 但对 $n$ 维 CW 复形 $X$, 上述关系变成$$X^0\subset X^1\subset \cdots \subset X^n=X,$$只有 $X^0$ 一定非零, $X^n$ 与前一项的差一定非零, 中间的包含关系都有可能相等. 例如对 CW 复形 ${\mathbb{S}}^n$ 就有 $X^0=X^1=\cdots =X^{n-1}$.

例 4.1.13. 对球面 $X={\mathbb{S}}^n$, 它有三角剖分 $h:X\to \left|K\right|$ 使得对任何的 $p⩽n-1$, 都有 $h{|}_{X^p}:X^p\to {\left|K\right|}^{(0)}$, 这因 $X^0=X^1=\cdots =X^{n-1}$, 而 $h:X\to \left|K\right|$.

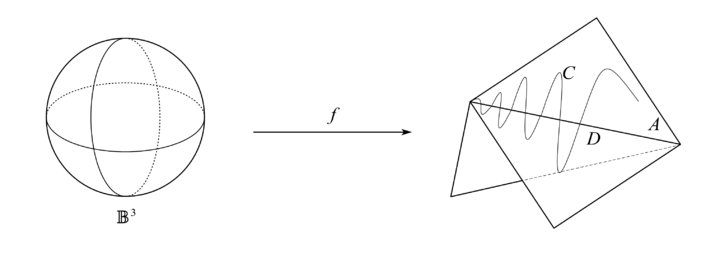
例 4.1.14 (不可三角剖分的 CW 复形). 下面构造一个不可三角剖分的 CW 复形, 考虑一个正方形粘上一个三角形构成的单纯复形 $K$, 其几何实现记作 $A$. 在正方形上存在一条曲线 $(x,\sin 1/x)$, 记作 $C$, 那么 $\bar{C}\subset A$. 将正方形与三角形相交的线记作 $D$, 并如此定义 CW 复形:

黏合映射 $g:\mathrm{Bd}{\mathbb{B}}^3\to \bar{C}\subset A$, 此时 $X=A{\bigsqcup }_g{\mathbb{B}}^3$ 具有 CW 复形结构, 并且映射$$\pi :A\bigsqcup {\mathbb{B}}^3\to A{\bigsqcup }_g{\mathbb{B}}^3$$满足 $\pi {|}_{\mathrm{Bd}{\mathbb{B}}^3}=g$, 于是 $\pi (\mathrm{Int}{\mathbb{B}}^3)=e_3$ 就是三角形内部构成的胞腔.

由此确定的 $X$ 是不可三角剖分的, 为了证明这一断言, 我们使用反证法. 否则, 存在单纯复形 $L$ 使得$$h:\left|L\right|\to X=(A\setminus C)\cup C\cup e_3$$是一个同胚.

首先考虑 ${\bar{e}}_3$, 取 $x\in e_3$ 有$$H_3(X,X\setminus x)\cong H_3({\mathbb{B}}^3,{\mathbb{B}}^3\setminus 0)\cong H_3({\mathbb{B}}^3,{\mathbb{S}}^2)\cong \mathbb{Z}.$$取 $x\in A\setminus C$ 有$$H_3(X,X\setminus X)\cong H_3({\mathbb{B}}^2,{\mathbb{B}}^2\setminus 0)=0$$中间的一项也可能是 $H_3({\mathbb{B}}_{+}^2,{\mathbb{B}}_{+}^2\setminus 0)$, 这源于切除公理中取 $U=X\setminus {\mathbb{B}}^2$ 或是 $U=X\setminus {\mathbb{B}}_{+}^2$, 取决于 $x$ 位于内部还是边界. 而对 $\sigma \in L$, $h(\mathrm{Int}\sigma )$ 不可能同时与 $e_3$ 和 $A\setminus C$ 相交. 这因对任何 $x,y\in \mathrm{Int}\sigma \subset \left|K\right|$, 都有$$H_p(\left|K\right|,\left|K\right|\setminus x)\cong H_p(\left|K\right|,\left|K\right|\setminus y).$$于是 $h(\mathrm{Int}\sigma )$ 或者是属于 ${\bar{e}}_3$ 的, 或者是属于 $A=\overline{A\setminus C}$ 的. 由此, ${\bar{e}}_3$ 和 $A$ 都分别可以三角剖分.

同样地, 断言 $D$ 也可以被 $h$ 三角剖分. 因 $D\subset A$, 取 $x\in \mathrm{Int}D$. 注意到 $A=x\ast \partial A$ 可缩, 由长正合序列可得$$H_2(A,A\setminus x)\cong H_1(A\setminus x)\cong \mathbb{Z}\oplus \mathbb{Z},$$这因此时 $A\setminus x$ 实际上同伦于 8 字形空间. 取 $x\in A\setminus D$, 就有$$H_2(A,A\setminus x)\cong \{\begin{array}{ll}{H}_2({\mathbb{B}}_{+}^2,{\mathbb{B}}_{+}^2\setminus 0),& x\in \partial A\setminus D\\ H_2({\mathbb{B}}^2,{\mathbb{B}}^2\setminus 0),& x\notin \partial A\end{array}$$于是对任意 $\sigma \in L$, 也有 $h(\mathrm{Int}\sigma )\cap D=\varnothing$, 那么 $h(\sigma )\subset D$, 于是 $D$ 也可以被 $h$ 三角剖分.

进而 $\bar{C}\cap D$ 也可被 $h$ 三角剖分. 但这不可能成立, 因为 $\bar{C}$ 与 $D$ 相交于无穷多个点.

直观上讲, 从一个离散点集 $X^0$ 开始, 在 $X^0$ 上定义离散拓扑. 按照如下的方式从 $X^{p-1}$ 构造 $X^p$: 将 ${\mathbb{D}}^p$ 通过黏合映射 $\phi :\mathrm{Bd}{\mathbb{D}}^p\to X^{p-1}$ 粘到 $X^{p-1}$ 上, 那么在拓扑和 $X^{p-1}\bigsqcup {\mathbb{D}}^p$ 上定义等价关系:$$\forall x\in \mathrm{Bd}{\mathbb{D}}^p(x\sim \phi (x)),$$从而 $X^p=X^{p-1}\bigsqcup {\mathbb{D}}^p/\sim$.

4.2CW 复形的结构

定理 4.2.1. 设 $X$ 是 $p$ 维的 CW 复形, 则

1.	$X=X^{p-1}{\bigsqcup }_g(\sum {\mathbb{D}}_{\alpha }^p)$, 这里 $\sum$ 表示拓扑和, $g:\sum \mathrm{Bd}{\mathbb{D}}_{\alpha }^p\to X^p$.
2.	设 $Y$ 是一个 CW 复形, $\dim Y⩽p-1$, $g:\sum \mathrm{Bd}{\mathbb{D}}_{\alpha }^p\to Y$ 使得 $g$ 将每一个 $\mathrm{Bd}{\mathbb{D}}_{\alpha }^p$ 映到有限多个 $Y$ 的开胞腔中. 那么 $X=Y{\bigsqcup }_g(\sum {\mathbb{D}}_{\alpha }^p)$ 是一个 CW 复形, 且 $Y=X^{p-1}$.

证明. (1) 设 $e_{\alpha }\subset X$ 是一个 $p$–开胞腔, 其示性映射 $f_{\alpha }:{\mathbb{D}}_{\alpha }^p\to {\bar{e}}_{\alpha }\subset X$. 令 ${\mathbb{D}}_{\alpha }^p={\mathbb{D}}^p\times \left\{\alpha \right\}$, 做拓扑和$$E=X^{p-1}\bigsqcup (\Sigma {\mathbb{D}}_{\alpha }^p).$$取 $g:\sum \mathrm{Bd}{\mathbb{D}}_{\alpha }^p\to X^p$ 满足 $g{|}_{\mathrm{Bd}{\mathbb{D}}_{\alpha }^p}=f_{\alpha }{|}_{\mathrm{Bd}{\mathbb{D}}_{\alpha }^p}$. 考虑映射$$\pi :E=X^{p-1}\bigsqcup (\Sigma {\mathbb{D}}_{\alpha }^p)\to X^{p-1}{\bigsqcup }_g(\Sigma {\mathbb{D}}_{\alpha }^p),$$它满足 $\pi {|}_{X^{p-1}}=\iota :X^p\hookrightarrow X$, $\pi {|}_{\sum \mathrm{Bd}{\mathbb{D}}_{\alpha }^p}=g$, $\pi {|}_{\sum \mathrm{Int}{D}_{\alpha }^p}=\sum f_{\alpha }{|}_{\sum \mathrm{Int}{\mathbb{D}}_{\alpha }^p}$. 只需要证明 $\pi$ 是商映射即可, 进而只需证它是闭映射, 也即 $C\subset X$ 是闭集当且仅当 ${\pi }^{-1}(C)$ 是闭集.

必要性是显然的, 因 $\pi$ 是连续的. 下设 ${\pi }^{-1}(C)$ 是闭集, 因$${\pi }^{-1}(C)\cap X^{p-1}=C\cap X^{p-1}$$是 $X^{p-1}$ 中的闭集, 于是对任意 $e_{\beta }\subset X^{p-1}$, 有$$C\cap {\bar{e}}_{\beta }=(C\cap X^{p-1})\cap {\bar{e}}_{\beta }$$是 ${\bar{e}}_{\beta }$ 中的闭集. 再考虑 ${\pi }^{-1}(C)\cap {\mathbb{D}}_{\alpha }^p$ 是 ${\mathbb{D}}_{\alpha }^p$ 中的闭集, 故对任何满足 $\dim e_{\alpha }=p$ 的开胞腔 $e_{\alpha }\subset X$, 因$$C\cap {\bar{e}}_{\alpha }=\pi ({\pi }^{-1}(C)\cap {\mathbb{D}}_{\alpha }^p)$$是 $X$ 中的紧子集 (因 $\pi$ 连续而后者是 $T_4$ 空间上紧集的闭子集, 从而仍是紧的), 从而是 $X$ 中的闭集. 因 $X$ 是 Hausdorff 的, 于是 $C\cap {\bar{e}}_{\alpha }$ 在 ${\bar{e}}_{\alpha }$ 中也是闭集, 那么弱拓扑导出 $C$ 是闭集.

(2) 有投射$$\pi :Y\bigsqcup (\Sigma {\mathbb{D}}_{\alpha }^p)\to X=Y{\bigsqcup }_g(\Sigma {\mathbb{D}}_{\alpha }^p),$$同样只需 $\pi$ 是商映射, 同样只需证它是闭映射. 必要性仍然是显然的, 因 $\pi$ 是连续的. 下设 ${\pi }^{-1}(C)$ 是闭集, 因为 $Y\bigsqcup (\sum {\mathbb{D}}_{\alpha }^p)$ 是 $T_4$ 的, 故 ${\pi }^{-1}(C)$ 是紧的. 因为 $\pi$ 连续, $\pi ({\pi }^{-1}(C))$ 在 $X$ 中是紧的, 从而是闭的.

那么 $X$ 的胞腔只有两种: 其一是 $Y$ 中 $\dim ⩽p-1$ 的开胞腔, 另一种是 $p$–开胞腔, 它们由 $\pi (\mathrm{Int}{\mathbb{D}}_{\alpha }^p)=e_{\alpha }$ 粘合而来. 因为$${\pi }^{-1}(\pi (\mathrm{Int}{\mathbb{D}}_{\alpha }^p))=\mathrm{Int}{\mathbb{D}}_{\alpha }^p\subset {\mathbb{D}}_{\alpha }^p$$是开集, 于是 $\pi {|}_{\mathrm{Int}{\mathbb{D}}_{\alpha }^p}:\mathrm{Int}{\mathbb{D}}_{\alpha }^p\to \pi (\mathrm{Int}{D}_{\alpha }^p)$ 是一个同胚, 此时 $\pi {|}_{{\mathbb{D}}_{\alpha }^p}=:f_{\alpha }$ 就是 $e_{\alpha }$ 的示性映射. 因此 $X$ 的确是一族不交开胞腔的并, 下面逐条验证它满足 CW 复形的定义:

(2a) $X$ 是 $T_4$ 的, 于是必然是 Hausdorff 的.

(2b) 对任意 $e_{\beta }\subset Y$, 因为 $Y$ 是 CW 复形, 那么在 $Y$ 上存在示性映射 $f_{\beta }:{\mathbb{D}}_{\beta }\to {\bar{e}}_{\beta }\subset Y\subset X$, 将其复合上一个嵌入映射就得到它在 $X$ 上的示性映射. 而对于 $e_{\alpha }\subset X\setminus Y$, 由前述讨论可知它的示性映射 $f_{\alpha }$ 即为 $\pi {|}_{{\mathbb{D}}_{\alpha }^p}$, 特别地, $f_{\alpha }{|}_{\mathrm{Bd}{\mathbb{D}}_{\alpha }^p}=g{|}_{\mathrm{Bd}{\mathbb{D}}_{\alpha }^p}$ 满足有限性.

(2c) 对 $C\subset X$, 若对任何 $e_{\alpha }\subset X$ 都有 $C\cap {\bar{e}}_{\alpha }$ 是 ${\bar{e}}_{\alpha }$ 中的闭集, 只需要 ${\pi }^{-1}(C)$ 也是闭集即可. 而这由$${\pi }^{-1}(C)={\pi }^{-1}(C)\cap (Y\cup (\Sigma {\mathbb{D}}_{\alpha }^p))=({\pi }^{-1}(C)\cap Y)\cup (\Sigma ({\pi }^{-1}(C)\cap {\mathbb{D}}_{\alpha }^p)).$$因 $Y$ 是 CW 复形, $\pi$ 限制到 $Y$ 上是嵌入, 于是 ${\pi }^{-1}(C)\cap Y=C\cap Y$ 借助在 $Y$ 上的弱拓扑是闭集. 而对后一项, 注意到$${\pi }^{-1}(C)\cap {\mathbb{D}}_{\alpha }^p={\pi }^{-1}(C\cap {\bar{e}}_{\alpha })\cap {\mathbb{D}}_{\alpha }^p$$因 $C\cap {\bar{e}}_{\alpha }$ 是闭的, 故 ${\pi }^{-1}(C\cap {\bar{e}}_{\alpha })$ 作为连续映射的原像是闭的, 而 $D_{\alpha }^p$ 是闭集, 从而 ${\pi }^{-1}(C)\cap {\mathbb{D}}_{\alpha }^p$ 也是闭集. 这就说明了 $X$ 上具有弱拓扑.

而此时新添加进来的胞腔都是 $p$ 维的, 于是 $Y=X^{p-1}$.

$\square$

4.3胞腔链复形

对 CW 复形 $X$, 其奇异链复形自然可以诱导出同调群, 但经过之前对于奇异同调的讨论不难发现, 奇异同调的确难以计算. 于是借助 CW 复形上的胞腔结构, 我们可以类似单纯链复形定义胞腔链复形. 在直观上, 胞腔链复形中的 $p$ 维链群就是由 $X$ 的 $p$–开胞腔生成的自由 Abel 群.

定义 4.3.1 (胞腔链复形). 设 $X$ 是 CW 复形, 有 $X^0\subset X^1\subset \cdots \subset X^p\subset \cdots$, 这是一列极限是 $X$ 的空间. 取$$D_p(X)=H_p(X^p,X^{p-1}),$$称作是 $X$ 的 $p$ 维胞腔链群. 边缘运算 $\partial :D_p(X)\to D_{p-1}(X)$ 通过以下的正合序列中的 $\partial =j_{\ast }{\partial }_{\ast }$ 确定. 称 $\mathcal{D}(X):=\left\{(D_p(X),\partial )\right\}$ 是 $X$ 的胞腔链复形.

命题 4.3.2. ${\partial }^2=0$.

证明. 这因注意到中间的一行是正合列即可.

$\square$

关于 $\partial :D_p(X)\to D_{p-1}(X)$ 的定义, 还可以从另一个角度来看待. 考虑三元组 $(X^p,X^{p-1},X^{p-2})$ 确定的正合列由 zig–zag 引理, 它诱导长正合列于是 $\partial$ 就是 ${\partial }_{\ast }$. (之后我们使用 ${\dot{e}}_{\alpha }$ 来表示之前的 $\partial e_{\alpha }$, 为了防止与这里定义的 $\partial$ 混淆.)

命题 4.3.3. 对单纯复形 $K$, $X=\left|K\right|$ 上有自然的 CW 复形结构. 此时 $H_p(\mathcal{D}(K))\cong H_p(\mathcal{S}(K))\cong H_p(\mathcal{C}(K))$.

证明. 因为对这样的 $X$, 有 $X=\left|K\right|$, $X^p=\left|K^{(p)}\right|$, 那么$$D_p(X)=H_p(X^p,X^{p-1})=H_p(K^{(p)},K^{(p-1)}),$$因为$$C_i(K^{(p)},K^{(p-1)})=\{\begin{array}{ll}0,& i\ne p\\ C_p(K^{(p)})=C_p(K),& i=p\end{array}$$于是 $\mathcal{C}(K^{(p)},K^{(p-1)})$ 只有在 $i=p$ 处非平凡, 于是 $D_p(K)=C_p(K)$. 这就证明了结论.

$\square$

我们先考虑粘上一个开胞腔的情况: 考虑 $e_{\alpha }\subset X$, $\dim e_{\alpha }=p$.

引理 4.3.4. 对 CW 复形 $X$ 中的 $p$–开胞腔 $e_{\alpha }$, 其示性映射$$f_{\alpha }:({\mathbb{D}}^p,{\mathbb{S}}^{p-1})\to ({\bar{e}}_{\alpha },{\dot{e}}_{\alpha })$$诱导了一个相对同调的同构.

证明. $n=0$ 时自然成立, 因此不妨假设 $n>0$. 取 $0\in {\mathbb{D}}^n$, 记 ${\hat{e}}_{\alpha }=f_{\alpha }(0)$, 则$$f_{\alpha }:{\mathbb{D}}^n\setminus 0\to {\bar{e}}_{\alpha }\setminus {\hat{e}}_{\alpha }$$仍是商映射. ${\mathbb{D}}^n\setminus 0$ 可以形变收缩到 ${\mathbb{S}}^{n-1}$, 于是 $H^{\prime }$ 可以由下图诱导: 此时有其中右侧的两个同胚分别取 $U=\mathrm{Bd}{\mathbb{B}}^n$ 和 $U={\dot{e}}_{\alpha }$ 由切除公理得到.

$\square$

我们考虑把所有的 $p$ 维开胞腔都粘上的情况, $D_p(X)=H_p(X^p,X^{p-1})$, $\sum f_{\alpha }:\sum ({\mathbb{D}}_{\alpha }^p,{\mathbb{S}}_{\alpha }^{p-1})\to (X^p,X^{p-1})$, 则对 $X^p=X^{p-1}{\bigsqcup }_g(\sum {\mathbb{D}}_{\alpha }^p)$. 这时黏合映射 $g:\sum (\mathrm{Bd}{\mathbb{D}}_{\alpha }^p)\to X^{p-1}$.

引理 4.3.5. $H_i(X^p,X^{p-1})\cong H_i(\sum {\mathbb{D}}_{\alpha }^p,\sum {\mathbb{S}}_{\alpha }^{p-1})\cong \underset{\alpha \in {\mathcal{A}}_p}{⨁}{H}_i({\mathbb{D}}_{\alpha }^p,{\mathbb{S}}_{\alpha }^{p-1})$.

证明. 考虑$$\pi :X^{p-1}\bigsqcup (\Sigma ({\mathbb{D}}_{\alpha }^p\setminus 0))\to X^{p-1}{\bigsqcup }_g(\Sigma ({\mathbb{D}}_{\alpha }^p\setminus 0)),$$而前者同伦于 $X^{p-1}\bigsqcup (\sum {\mathbb{S}}_{\alpha }^{p-1})$, 后者即为 $\pi (X^{p-1}\bigsqcup (\sum {\mathbb{D}}_{\alpha }^p\setminus 0))=X^{p-1}\bigsqcup (\sum {\bar{e}}_{\alpha }\setminus {\hat{e}}_{\alpha })$, 而这同伦于 $X^{p-1}$. 类似地有而最右侧的 $\pi$ 是同胚. 于是$$H_i(X^p,X^{p-1})\cong H_i(\Sigma {\mathbb{B}}_{\alpha }^p,\Sigma \mathrm{Bd}{\mathbb{D}}_{\alpha }^p)\cong \underset{\alpha }{⨁}{H}_i({\bar{e}}_{\alpha },{\dot{e}}_{\alpha }),$$且只有 $i=p$ 时, 右侧是非零的. 并且 $H_p(X^p,X^{p-1})={\mathbb{Z}}^{\oplus |{\mathcal{A}}_p|}$.

$\square$

尽管链复形中的 $D_p(X)$ 看起来非常显然, 这里 $\left|{\mathcal{A}}_p\right|$ 就是 $p$–开胞腔的个数, 但此时 $\partial$ 的具体确定却成为了难点. 特别地, 若 $X$ 是可以三角剖分的 CW 复形时, $\partial$ 的确定相对容易一些, 这因为 $\partial$ 和链映射的交换性可以让我们直接对单纯复形讨论边缘算子.

4.4胞腔同调与奇异同调的等价性

在讨论与奇异同调的关系之前, 我们首先说明胞腔复形的所谓定向. 对 $\alpha \in {\mathcal{A}}_p$, 有 $H_p({\bar{e}}_{\alpha },{\dot{e}}_{\alpha })\cong \mathbb{Z}$, 后者有生成元 $\pm 1$, 于是 $H_p({\bar{e}}_{\alpha },{\dot{e}}_{\alpha })$ 的生成元就确定了 $e_{\alpha }$ 的定向.

定理 4.4.1. 设 $X$ 是 CW 复形, 则 $H_p(\mathcal{D}(X))\cong H_p(\mathcal{S}(X))$.

证明. 当 $X=\left|K\right|$ 时已经证明过了, 我们考虑一般情况. 直接计算这涉及四个骨架 $(X^{p+1},X^p,X^{p-1},X^{p-2})$, 它产生了四个三元组$$(X^{p+1},X^p,X^{p-1}),(X^{p+1},X^p,X^{p-2}),(X^{p+1},X^{p-1},X^{p-2}),(X^p,X^{p-1},X^{p-2}).$$于是我们得到这样的辫子: 其中所有相同颜色的态射链是正合的.

因 $k_{\ast }$ 是单的, 有 $\mathrm{im}{k}_{\ast }\cong H_p(X^p,X^{p-2})$, 而 $H_p(X^p,X^{p-1})$ 处的正合性保证 $\mathrm{im}{k}_{\ast }=\ker {\partial }_p$. 于是 $l_{\ast }{k}_{\ast }^{-1}:\mathrm{im}{k}_{\ast }\to H_p(X^{p+1},X^{p-2})$. 我们断言 $\ker l_{\ast }{k}_{\ast }^{-1}=\mathrm{im}{\partial }_{p+1}$, 这样由第一同构定理就有 $H_p(\mathcal{D}(X))\cong H_p(X^{p+1},X^{p-2})$.

下面证明这一断言, 这因$$\begin{array}{rl}\alpha \in \ker l_{\ast }{k}_{\ast }^{-1}& ⟹l_{\ast }{k}_{\ast }^{-1}(\alpha )=0\\ & ⟹k_{\ast }^{-1}(\alpha )\in \ker l_{\ast }=\mathrm{im}{\partial }_{\ast }^{\prime \prime }\\ & ⟹\exists \beta \in D_{p+1}(X)({\partial }_{\ast }^{\prime \prime }(\beta )=k_{\ast }^{-1}(\alpha ))\\ & ⟹\alpha =k_{\ast }{\partial }_{\ast }^{\prime \prime }(\beta )={\partial }_{p+1}(\beta )\\ & ⟹\alpha \in \mathrm{im}{\partial }_{p+1}\end{array}$$和$$\begin{array}{rl}\alpha \in \mathrm{im}{\partial }_{p+1}& ⟹\exists \beta \in D_{p+1}(X)({\partial }_{\ast }(\beta )={\ker }_{\ast }{\partial }_{\ast }^{\prime \prime }(\beta )=\alpha )\\ & ⟹{\partial }_{\ast }^{\prime \prime }(\beta )=k_{\ast }^{-1}(\alpha )\in \mathrm{im}{\partial }_{\ast }^{\prime \prime }=\ker l_{\ast }\\ & ⟹l_{\ast }{k}_{\ast }^{-1}(\alpha )=0\end{array}$$得证.

接下来只需$$H_p(X^{p+1},X^{p+2})\cong H_p(X^{p+1})\cong H_p(\mathcal{S}(X))=H_p(X)$$即可.

先来证明第一个同胚, 我们考虑 $i⩽p-2$ 是的三元组 $(X^{p+1},X^i,X^{i-1})$, 有长正合序列$$\to H_p(X^i,X^{i-1})\to H_p(X^{p+1},X^{i-1})\to H_p(X^{p+1},X^i)\to H_{p-1}(X^i,X^{i-1})\to$$注意到首尾都是 $0$, 因此 $H_p(X^{p+1},X^{i-1})\cong H_p(X^{p+1},X^i)$ 对任何 $i⩽p-2$ 成立. 于是 $H_p(X^{p+1},X^{p-2})\cong H_p(X^{p+1},X^{-1})=H_p(X^{p+1})$.

再来证明第二个同胚, 因 $\iota :X^{p+1}\hookrightarrow X$ 诱导的 ${\iota }_{\ast }$ 为同构 (这一点我们放在后面说明), 对 $i⩾1$, 考虑 $(X^{p+i+1},X^{p+i})$, 有长正合序列$$\to H_{p+1}(X^{p+i+1},X^{p+i})\to H_p(X^{p+i})\to H_p(X^{p+i+1})\to H_p(X^{p+i+1},X^{p+i})\to$$注意到首尾都是 $0$, 于是 $H_p(X^{p+i})\cong H_p(X^{p+i+1})$. 因此 $H_p(X^{p+1})\cong H_p(X^{p+2})\cong \cdots \cong H_p(X)$.

下面我们说明 ${\iota }_{\ast }$ 是同构. 任取 $\beta \in H_p(\mathcal{S}(X))$, 则存在紧子集 $K$, $j:K\hookrightarrow X$ 使得 $j_{♯}(\sum n_{T}T)=\sum n_{T}T$ 被 $K$ 承载. 故 $\beta \in \mathrm{im}[j_{\ast }:H_p(K)\to H_p(X)]$. 而另一方面, 存在正整数 $k$ 使得 $j^{\prime }:K\hookrightarrow X^{p+k}$, 故$$\beta \in \mathrm{im}[j_{\ast }^{\prime }:H_p(K)\to H_p(X^{p+k})\cong H_p(X^{p+1})],$$于是 $\beta \in {\iota }_{\ast }[H_p(X^{p+1})\to H_p(X)]$, 即 ${\iota }_{\ast }$ 是满同态.

再令 ${\iota }_{\ast }(\beta )=0$, $\beta \in H_p(X^{p+1})$, 那么 ${\iota }_{\ast }:H_p(X^{p+1})\to H_p(X)$, 故存在紧子集 $K$ 使得 $j:X^{p+1}\hookrightarrow K$ 使得 $j_{\ast }:H_p(X^{p+1})\to H_p(K)$ 满足 $j_{\ast }(\beta )=0$. 另一方面, 存在正整数 $k$ 使得 $j^{\prime }:K\hookrightarrow X^{p+k}$ 满足 $j_{\ast }^{\prime }{j}_{\ast }(\beta )=0$, 而这说明 $\beta =0$, 即 ${\iota }_{\ast }$ 是单同态.

$\square$

4.5应用: 射影空间

对拓扑空间 $X$, 我们考虑这样的一列集合:

定义 4.5.1 (滤子). 对拓扑空间 $X$, 若存在一列集合 $(X_p{)}_{p\in {\mathbb{Z}}_{⩾0}}$ 使得$$X_0\subset X_1\subset \cdots \subset X_p\subset \cdots$$且 $X=\bigcup _{p\in {\mathbb{Z}}_{⩾0}}{X}_p$, 则称 $(X_p{)}_{p\in {\mathbb{Z}}_{⩾0}}$ 是 $X$ 的一个滤子, 同样地定义 $D_p(X)=H_p(X_p,X_{p-1})$.

但需要注意这时的 $D_p(X)$ 未必是自由 Abel 群, 并且 $H_i(X_p,X_{p-1})$ 在 $i\ne p$ 处也未必是平凡的.

下面考虑 ${\mathbb{RP}}^n=\left\{l\subset {\mathbb{R}}^n:\dim l=1\right\}$, 类似地有 ${\mathbb{CP}}^n=\left\{l\subset {\mathbb{C}}^n:\dim l=1\right\}$. 将 ${\mathbb{RP}}^n$ 视作 ${\mathbb{S}}^n/{\sim }_p$, 这里 $p$ 是商映射, 为此只需 $p$ 是闭映射即可. 对 $A\subset {\mathbb{S}}^n$ 是闭集, 有$$p^{-1}(p(A))=A\cup r(A)$$是闭集, 故 $p(A)$ 是闭的, 也即 $p$ 是闭映射.(这里 $r$ 是对径映射)

由点集拓扑可知 ${\mathbb{RP}}^n$ 是 Hausdorff 的.

命题 4.5.2. ${\mathbb{RP}}^n$ 是一个 CW 复形, 当 $0⩽p⩽n$ 时, 它恰有一个 $p$–开胞腔, 且 $X^p={\mathbb{RP}}^p$.

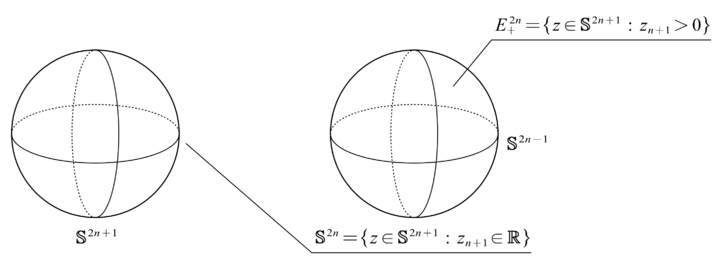
证明. 当 $n=0$ 时, ${\mathbb{RP}}^0$ 是一个单点, 命题自然是成立的. 归纳假设当 $⩽n-1$ 时都成立. 视 ${\mathbb{RP}}^n$ 是由 $p:{\mathbb{S}}^n\to {\mathbb{RP}}^n$ 作用而来, 它将 $x$ 与 $-x$ 等同. 那么将 $p$ 限制到 $E_{+}^n$ 上得到$$p_{+}:E_{+}^n\to {\mathbb{RP}}^n,x\mapsto [x]=\left\{x,-x\right\}$$仍是一个商映射 (这因 $x$ 和 $-x$ 总有一个落在 $E_{+}^n$ 中). 注意到 $\mathrm{Bd}{E}_{+}^n={\mathbb{S}}^{n-1}$, 而 $p_{+}{|}_{\mathrm{Bd}{E}_{+}^n}:{\mathbb{S}}^{n-1}\to {\mathbb{RP}}^{n-1}$, 由此$$p{|}_{\mathrm{Int}{E}_{+}^n}:\mathrm{Int}{E}_{+}^n\to {\mathbb{RP}}^n\setminus {\mathbb{RP}}^{n-1}=:e_n$$是一个同胚, 并且 $p_{+}$ 实际上就是黏合映射.

$\square$

这里 $p$ 可以看作是 $\mathbb{Z}/2\mathbb{Z}$ 在 ${\mathbb{S}}^n$ 上的作用. 从上述讨论中我们可以得到一串结构:$${\mathbb{RP}}^0\subset {\mathbb{RP}}^1\subset \cdots \subset {\mathbb{RP}}^n\subset \cdots \subset {\mathbb{RP}}^{\infty }=\bigcup _{n⩾0}{\mathbb{RP}}^n,$$称 ${\mathbb{RP}}^{\infty }$ 是无穷维实射影空间, 它在每个维数 $p$ 上都有一个开胞腔 ${\mathbb{RP}}^p$. 那么同样地, 考虑一列球面, 将前一个视作后一个的赤道得到$${\mathbb{S}}^0\subset {\mathbb{S}}^1\subset \cdots \subset {\mathbb{S}}^n\subset \cdots \subset {\mathbb{S}}^{\infty }=\bigcup _{n⩾0}{\mathbb{S}}^n,$$称 ${\mathbb{S}}^{\infty }$ 是一个无穷维球面. 有趣的是, 尽管每一个 ${\mathbb{S}}^n$ 都不是可缩的, 但 ${\mathbb{S}}^{\infty }$ 却是可缩的.

下面计算 ${\mathbb{RP}}^n$ 的同调. 考虑到其 CW 复形结构, 其胞腔链群 $D_p({\mathbb{RP}}^n)\cong \mathbb{Z},0⩽p⩽n$ 是显然的. 下面我们计算边缘映射 $\partial :D_p({\mathbb{RP}}^n)\to D_{p-1}({\mathbb{RP}}^n)$. 考虑下面的交换图:则$$\partial =j_{\ast }{\partial }_{\ast }^{\prime }=j_{\ast }{p}_{\ast }{\partial }_{\ast }(p{|}_{E_{+}^{p+1}}{)}_{\ast }^{-1}=(j_{\ast }{p}_{\ast })({\partial }_{\ast }(p{|}_{E_{+}^{p+1}}{)}_{\ast }^{-1}),$$其中 $j_{\ast }{p}_{\ast }$ 确定了 $\partial$ 究竟是一个怎样的同态. 将上图中所有涉及到的同态列出来:$$\begin{array}{rl}{j}_{\ast }{p}_{\ast }& :\mathbb{Z}\cong H_p({\mathbb{S}}^p)\stackrel{p_{\ast }}{⟶}{H}_p({\mathbb{RP}}^p)\stackrel{j_{\ast }}{⟶}{H}_p({\mathbb{RP}}^p,{\mathbb{RP}}^{p-1})\cong \mathbb{Z},\\ p& :{\mathbb{S}}^p\to {\mathbb{RP}}^p\\ p{|}_{E_{+}^{n+1}}& :(E_{+}^{p-1},{\mathbb{S}}^p)\to ({\mathbb{RP}}^p,{\mathbb{RP}}^{p-1})\hookrightarrow ({\bar{e}}_{\alpha }^p,{\dot{e}}_{\alpha }^p)\end{array}$$因 $X={\mathbb{RP}}^n$ 可以三角剖分, 这里对 $n=1$ 的情形取如下的三角剖分, 对 $n>1$ 的情形考虑通常的八面体剖分做一次重心重分即可, 记对应的单纯复形为 $K$.

那么对 $e_{\alpha }^p\subset X^p\setminus X^{p-1}$, 它落在 $K$ 的一个开单形中, 即 ${\bar{e}}_{\alpha }$ 可被 $K$ 的子复形三角剖分. 因此, 对 $H_p({\bar{e}}_{\alpha },{\dot{e}}_{\alpha })$ 的计算可以归结为对单纯同调的计算. 我们称 $H_p({\bar{e}}_{\alpha },{\dot{e}}_{\alpha })$ 的生成元为一个基本闭链.

命题 4.5.3. $\partial :D_{p+1}({\mathbb{RP}}^n)\to D_p({\mathbb{RP}}^n)$ 在 $0⩽p=2k+1⩽n$ 时是将基本闭链 $\times 2$ (这一映射之后也直接记作 $\times 2$), 当 $p=2k$ 时 $\partial =0$.

证明. 取 $H_p(E_{+}^p,{\mathbb{S}}^{p-1})$ 中的一个基本闭链 $\left\{c_p\right\}$, 那么 $c_p\in Z_p(E_{+}^p,{\mathbb{S}}^{p-1})$, 于是 $\partial c_p$ 被 ${\mathbb{S}}^{p-1}$ 承载. 构造$${\gamma }_p=c_p+(-1{)}^{p-1}{r}_{♯}(c_p),$$这里 $r$ 是对径映射, $r_{♯}(c_p)$ 是 $H_p(E_{-}^p,{\mathbb{S}}^{p-1})$ 的生成元, 它被 ${\mathbb{S}}^p$ 承载. 计算$$\partial {\gamma }_p=\partial c_p+(-1{)}^{p-1}{r}_{♯}(\partial c_p)=\partial c_p+(-1{)}^{p-1}(-1{)}^{p+1}\partial c_p=0.$$于是 $\left\{{\gamma }_p\right\}$ 是 $H_p({\mathbb{S}}^p)$ 的生成元, 那么注意到故有 $p=pr$. 直接计算$$\begin{array}{rl}{j}_{♯}{p}_{♯}(c_p+(-1{)}^{p-1}{r}_{♯}(c_p))& =j_{♯}(p_{♯}(c_p)+(-1{)}^{p-1}{p}_{♯}{r}_{♯}(c_p))\\ & =j_{♯}(p_{♯}{r}_{♯}(c_p)+(-1{)}^{p-1}{p}_{♯}{r}_{♯}(c_p))\\ & =j_{♯}{p}_{♯}((1+(-1{)}^{p-1})c_p)\end{array}$$可知命题成立.

$\square$

定理 4.5.4. 实射影空间 ${\mathbb{RP}}^n$ 的同调群如下: $${\tilde{H}}_p({\mathbb{RP}}^{2n+1})=\{\begin{array}{ll}\mathbb{Z}/2\mathbb{Z},& p=2k+1,0⩽k<n\\ \mathbb{Z},& p=2n+1\\ 0,& \text{其他}\end{array},{\tilde{H}}_p({\mathbb{RP}}^{2n})=\{\begin{array}{ll}\mathbb{Z}/2\mathbb{Z},& p=2k+1,0⩽k<n\\ 0,& \text{其他}\end{array}$$特别地, $${\tilde{H}}_p({\mathbb{RP}}^{\infty })=\{\begin{array}{ll}\mathbb{Z}/2\mathbb{Z},& p=2k+1,k⩾0\\ 0,& \text{其他}\end{array}$$

证明. 直接考虑长正合列和即可.

$\square$

这同时说明了 ${\mathbb{RP}}^{2n+1}$ 是可定向的, 但是 ${\mathbb{RP}}^{2n}$ 不可定向.

相交于实射影空间的情形, 复射影空间的 CW 复形结构和同调群都更简单一些.

命题 4.5.5. $X={\mathbb{CP}}^n$ 是一个 CW 复形, 对 $p⩽n$, $X$ 恰有一个 $2p$–开胞腔, 且 $X^{2p}={\mathbb{CP}}^n$. 它没有任何奇数维开胞腔. 此时同调群的结果显而易见: $$H_p({\mathbb{CP}}^n)=\{\begin{array}{ll}\mathbb{Z},& p=2k,0⩽k⩽n\\ 0,& \text{其他}\end{array}$$

证明. 考虑这样的嵌入: $$\rho :{\mathbb{C}}^{n+1}\to {\mathbb{R}}^{2n+2},(z_1,z_2,\dots ,z_{n+1})\mapsto (\mathrm{Re}{z}_1,\mathrm{Im}{z}_1,\dots ,\mathrm{Re}{z}_{n+1},\mathrm{Im}{z}_{n+1}),$$并且在 ${\mathbb{R}}^{2n+2}$ 上注意到 $\Vert \rho (z)\Vert =\Vert z\Vert$, 于是它是一个同胚. 在后续的讨论中, 我们在合适的时候使用核是的空间.

视 ${\mathbb{CP}}^n$ 是 ${\mathbb{C}}^{\infty }$ 的子集, 它可以看作 ${\mathbb{S}}^{2n+1}/{\mathbb{S}}^1$, 也即在 $n+1$ 维复球面 ${\mathbb{S}}^{2n+1}$ 上定义这样的等价关系: 当 $\left|\lambda \right|=1$, 也即 $\lambda \in {\mathbb{S}}^1$ 时, $$(z_1,z_2,\dots ,z_{n+1},0,\dots )\sim (\lambda z_1,\lambda z_2,\dots ,\lambda z_{n+1},0,\dots ).$$记$$p:{\mathbb{S}}^{2n+1}\to {\mathbb{CP}}^n\cong {\mathbb{S}}^{2n+1}/{\mathbb{S}}^1,$$下面证明 $p$ 是商映射. 为此只需 $p$ 是闭映射. 设 $A\subset {\mathbb{S}}^{2n+1}$ 是闭子集, 则 $p^{-1}p(A)=l({\mathbb{S}}^1\times A)$, 这里$$l:{\mathbb{S}}^1\times {\mathbb{S}}^{2n+1}\to {\mathbb{S}}^{2n+1},(\lambda ,z)\mapsto \lambda z$$是一个自由作用 (即没有不动点的作用), 那么 $l({\mathbb{S}}^1\times A)$ 是紧集, 从而是闭的. 由此 $p(A)$ 也是闭集, 这就说明了 $p$ 是闭映射.

考虑下面的作用:

只需证明$$p{|}_{\mathrm{Int}{E}_{+}^{2n}}:\mathrm{Int}{E}_{+}^{2n}\to {\mathbb{CP}}^n\setminus {\mathbb{CP}}^{n-1}=:e_{\alpha }^{2n}$$是一个同胚即可.(这因 ${\mathbb{S}}^{2n-1}$ 是复球面的复赤道)

它是单的, 因对 $z,z^{\prime }$ 满足 $p(z)=p(z^{\prime })$, 存在 $\lambda \in {\mathbb{S}}^1$ 使得 $z=\lambda z^{\prime }$, 于是 $z_{n+1}=\lambda z_{n+1}^{\prime }$. 但 $z_{n+1}>0$, $z_{n+1}^{\prime }>0$, 于是 $\lambda >0$. 而 $\lambda \in {\mathbb{S}}^1$, 只能 $\lambda =1$, 这即 $z=z^{\prime }$.

它是满的, 因对任意 $a\in e_{\alpha }^{2n}$, 存在 $z\in {\mathbb{S}}^{2n+1}\setminus {\mathbb{S}}^{2n-1}$, $\left|z\right|=1$ 满足 $z_{n+1}=r{\mathrm{e}}^{\mathrm{i}\theta }$, 这里 $r>0$. 那么取 $\lambda ={\mathrm{e}}^{-\mathrm{i}\theta }$ 之后就有 $\lambda z_{n+1}=r>0$, 于是 $\lambda z\sim z\in \mathrm{Int}{E}_{+}^{2n}$, 这即 $p(z)=p(\lambda z)\in p(\mathrm{Int}{E}_{+}^{2n})$.

$\square$