1. 单纯同调论

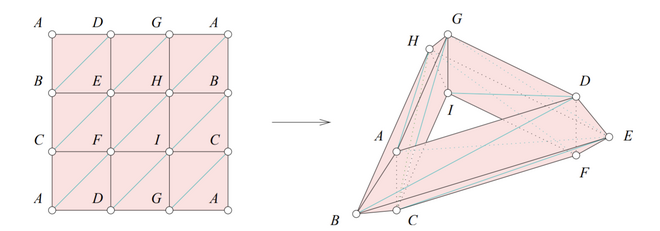
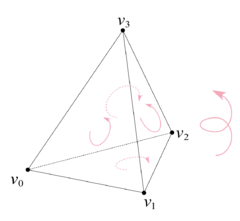1.1几何复形

首先声明我们主要讨论的基底空间 ${\mathbb{R}}^{\mathbb{N}}$. 记$${\mathbb{R}}^{\mathbb{N}}:=\left\{(x_1,x_2,\dots ,x_n,\dots ):\text{至多有限个 }{x}_i\text{ 非零}\right\},$$在其上可以定义凝聚拓扑, 即$$A\subset {\mathbb{R}}^{\mathbb{N}}\text{ 是闭集}⟺\forall n\in \mathbb{N},A\cap {\mathbb{R}}^n\text{为}{\mathbb{R}}^n\text{中闭集}.$$

考虑 $a_0,\dots ,a_p$ 是 ${\mathbb{R}}^{\mathbb{N}}$ 中的 $p+1$ 个点, 称它们几何独立, 若 $\left\{a_1-a_0,\dots ,a_p-a_0\right\}$ 线性无关. 这确定了一个 $p$ 维线性空间$$P:=\mathrm{span}\left\{a_1-a_0,\dots ,a_p-a_0\right\}=\left\{\sum _{i=1}^p{\lambda }_i(a_i-a_0):{\lambda }_i\in \mathbb{R}\right\},$$将其平移得到仿射空间 $a_0+P$. 此时$$a_0+P=\left\{\left(1-\sum _{i=1}^p{\lambda }_i\right)a_0+\sum _{i=1}^p{\lambda }_i{a}_i:{\lambda }_i\in \mathbb{R}\right\}=\left\{\sum _{i=0}^p{\lambda }_i{a}_i:\sum _{i=0}^p{\lambda }_i=1\right\},$$其中 ${\lambda }_0=1-\sum _{i=1}^p{\lambda }_i$. 注意到几何独立的 $p+1$ 个点把空间划分成不同的区域, 我们将依此定义单形.

定义 1.1.1 ($p$ 维单形, 真面). 设 $a_0,\dots ,a_p$ 是 ${\mathbb{R}}^{\mathbb{N}}$ 中几何独立, 称$$(a_0,\dots ,a_p):=\left\{\sum _{i=0}^p{\lambda }_i{a}_i:\sum _{i=0}^p{\lambda }_i=1,{\lambda }_i⩾0\right\}$$是一个 ${\mathbb{R}}^{\mathbb{N}}$ 中的 $\mathbf{p}$ 维单形.

若 $\left\{i_0,\dots ,i_q\right\}\subset \left\{0,\dots ,p\right\}$, 则 $a_{i_0},\dots ,a_{i_q}$ 几何独立, 记$${\tau }^q=(a_{i_0},\dots ,a_{i_q})\prec (a_0,\dots ,a_p)={\sigma }^p.$$若 $q<p$, 称 ${\tau }^q$ 是 ${\sigma }^p$ 的一个真面.

单形是最简单的几何体, 单形的组合构成更复杂的几何体.

定义 1.1.2 (复形). 设 $K$ 是 ${\mathbb{R}}^{\mathbb{N}}$ 中一些单形的集合, 称 $K$ 是一个 (单纯) 复形, 若

1.	对任意 $\sigma \in K$, $\sigma$ 的任何面仍在 $K$ 中;
2.	对任意 $\sigma ,\tau \in K$, $\sigma \cap \tau$ 或者是空集, 或者是它们的公共面.

若 $K$ 中的单形个数有限, 则称 $K$ 是有限复形.

这说明由单形搭建复形是有一定规则的: 例如下图中左图是复形而右图不是复形.

定义 1.1.3 (复形的维数). 设 $K$ 是一个复形, 称其维数为$$\dim K:=\underset{\sigma \in K}{\sup }\dim \sigma .$$有限复形必是有限维的, 但反之不真.

对一个单形 ${\sigma }^p\in {\mathbb{R}}^{\mathbb{N}}$, 可以从此出发构造复形$$K_{{\sigma }^p}:=\left\{\tau :\tau \prec {\sigma }^p\right\}$$和其边界复形$$\mathrm{Bd}{K}_{{\sigma }^p}=K_{\partial {\sigma }^p}:=K_{{\sigma }^p}\setminus \left\{\sigma \right\}.$$更具体一些, 有复形的骨架的概念:

定义 1.1.4 (骨架). 设 $K$ 是一个复形, 称$$K^{(p)}:=\left\{\sigma \in K:\dim \sigma ⩽p\right\}$$是 $K$ 的 $\mathbf{p}$ 维骨架. 于是 $K^{(p)}$ 也是一个复形, $K^{(p)}\subset K$ 是 $K$ 的一个子复形. 特别地, $K^{(0)}$ 称作是 $K$ 的顶点集, 其中的元素称作 $K$ 的顶点.

直观上当 $p=1$ 时, $1$ 维骨架就是直观上看起来的复形的 “骨架”, 它只包含复形的 $0$ 维子复形 (即顶点) 和 $1$ 维子复形 (即各边).

设 $K$ 是 ${\mathbb{R}}^{\mathbb{N}}$ 的复形, 称$$\left|K\right|=\bigcup _{\sigma \in K}\sigma$$是 $K$ 的几何实现或伴随多面体. 此时 $\left|K\right|$ 成为 ${\mathbb{R}}^{\mathbb{N}}$ 中的子集, 赋予拓扑 ${\mathcal{T}}_{|K|}$ 是 ${\mathbb{R}}^{\mathbb{N}}$ 上的子空间拓扑.

引理 1.1.5. 设 $L$ 是 $K$ 的子复形, 则 $\left|L\right|$ 是 $\left|K\right|$ 中的闭集.

证明. 设 $A\subset \left|L\right|$ 是闭集, 对任意 $\sigma \in K$, 有$$\sigma \cap \left|L\right|=\bigcup _{\tau \prec \sigma ,\tau \in L}\tau ,$$故$$A\cap \sigma =\bigcup _{\tau \prec \sigma ,\tau \in L}(A\cap \tau ).$$而 $A\cap \tau$ 是 $\tau$ 中的闭集, 且 $\tau \prec \sigma$, 故 $A\cap \tau$ 是 $\sigma$ 中的闭集, 进而 $A\cap \sigma$ 也是 $\sigma$ 中的闭集. 由此可知 $A$ 是 $\left|K\right|$ 中的闭集.

特别地, 取 $A=\left|L\right|$ 即可证明引理.

$\square$

由此可以说明在 $\left|K\right|$ 上的拓扑在一般情形下是弱于 Euclid 拓扑的, 即使它可以被嵌入有限维空间. 为此考虑复形$$K=\left\{[m,m+1]:m\ne 0,m\in \mathbb{Z}\right\}\cup \left\{[\frac{1}{n+1},\frac{1}{n}]:n\in {\mathbb{Z}}_{+}\right\}\cup \mathbb{Z}\cup \left\{\frac{1}{n}:n\in {\mathbb{Z}}_{+}\right\}.$$则 $\left|K\right|=\mathbb{R}$, 且 $L=\left\{1/n:n\in {\mathbb{Z}}_{+}\right\}$ 是 $K$ 的子复形. 由引理 1.1.5 可知 $\left|L\right|=L$ 是 $\left|K\right|$ 中的闭集, 但在 $\left|K\right|$ 的 Euclid 拓扑下 $\left|L\right|$ 并不是闭集, 因它有聚点 $0\notin \left|L\right|$.

定义 1.1.6 (可三角剖分空间). 称拓扑空间 $X$ 可三角剖分, 若存在复形 $K$ 使得 $X\cong \left|K\right|$.

所有的光滑流形都可以被三角剖分, 一个例子是环面 ${\mathbb{T}}^2$ 可以被下图三角剖分:

图 1. ${\mathbb{T}}^2$ 的三角剖分

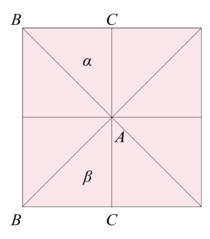
但需要注意的是下图的剖分方式并不是三角剖分, 因标注 $\alpha$ 和 $\beta$ 的两个三角形同时相交于点 $A$ 和线 $BC$, 它们不是公共面 (因不连通).

图 2. 一种不是三角剖分的 ${\mathbb{T}}^2$ 的剖分方式

1.2单纯映射

单纯复形范畴可以看作偏序范畴的一种, 考虑由真面诱导的偏序 $\prec$, 那么 $(K,\prec )$ 构成一个偏序集, 因此我们需要保持偏序结构的态射:

定义 1.2.1 (单纯映射). 称 $f:K\to L$ 是一个单纯映射, 若对任意 $\sigma \in K$ 都有 $f(\sigma )\in L$, $f$ 保持偏序关系, 即$$\tau \prec \sigma ⟹f(\tau )\prec f(\sigma ),$$同时要求 $\dim f(\sigma )⩽\dim \sigma$.

这与教材上的定义是等价的. $\dim f(\sigma )⩽\dim \sigma$ 保证了 $f$ 将 $K$ 的顶点 $K^{(0)}$ 映到 $L$ 的顶点 $L^{(0)}$. 单形本质上就可以看作是一些顶点的集合 (由习题 1.1 保证). 于是单纯映射可以作为态射, 构成一个范畴 $\mathsf{SimComp}$, 称作是单纯复形范畴.

单纯映射 $f:K\to L$ 诱导一个拓扑空间之间的映射 $g_f$, 它满足$$g_f:\left|K\right|\to \left|L\right|,x=\sum _{i=0}^p{t}_i{\sigma }_i\mapsto \sum _{i=0}^p{t}_{i}f({\sigma }_i),$$它可以看作是一系列形如 $g_f{|}_{\sigma }:\sigma \mapsto \left|L\right|$ 拼接起来的映射. 在拓扑空间范畴 $\mathsf{Top}$ 中, 我们当然希望 $g_f$ 是连续的, 从而导出一个 $\mathsf{SimComp}$ 到 $\mathsf{Top}$ 的函子. 为此先证明以下引理:

引理 1.2.2. $h:\left|K\right|\to X$ 连续当且仅当对任意 $\sigma \in K$, 都有 $h{|}_{\sigma }:\sigma \to X$ 连续.

证明. 必要性. 显然.

充分性. 任取 $X$ 上的闭集 $C$, 对任意 $\sigma \in K$, 只需要证明 $h^{-1}(C)\cap \sigma$ 是 $\sigma$ 中的闭集即可. 而$$h^{-1}(C)\cap \sigma =(h{|}_{\sigma }{)}^{-1}(C)$$是闭的.

$\square$

由此得到:

命题 1.2.3. $F:K\mapsto \left|K\right|,f\mapsto g_f$ 给出一个 $\mathsf{SimComp}$ 到 $\mathsf{Top}$ 的函子.

证明. 只需验证 $F$ 的函子性, 首先 ${\mathrm{id}}_K:K\to K$ 诱导出 $F({\mathrm{id}}_K)={\mathrm{id}}_{|K|}:\left|K\right|\to \left|K\right|$, 于是只需要证明图交换即可. 这因$$g_{hf}(x)=\sum _{i=0}^p{t}_i(hf)({\sigma }_i)=g_h\sum _{i=0}^p{t}_{i}f({\sigma }_i)=g_h{g}_f(x).$$$\square$

对复形 $K$, 其中的单形 $\sigma =({\sigma }_0,\dots ,{\sigma }_p)$ 可以由顶点集 $\left\{{\sigma }_0,\dots ,{\sigma }_p\right\}$ 描述, 因此 $K$ 在某种程度上可以由 $K^{(0)}$ 描述.

定义 1.2.4 (抽象复形). 设 $S$ 是一个集合, 称 $\mathcal{K}\subset 2^S$ 是一个抽象复形, 若$$\forall s\in \mathcal{K}(t\subset s⟹t\in \mathcal{K}).$$此时的 $s$ 即为抽象单形, $\dim s=\left|s\right|-1$. 特别地, $\dim \varnothing =-1$. 类似可定义抽象复形的维数$$\dim \mathcal{K}:=\underset{s\in \mathcal{K}}{\sup }\dim s.$$对抽象复形, 也可以定义骨架 ${\mathcal{K}}^{(p)}:=\left\{s\in \mathcal{K}:\dim s⩽p\right\}$.

定义 1.2.5 (几何实现复形). 称 $K$ 是 $\mathcal{K}$ 的几何实现复形, 若存在双射 $f:K^{(0)}\to {\mathcal{K}}^{(0)}$ 使得$$(v_0,\dots ,v_p)\in K⟺\left\{f(v_0),\dots ,f(v_p)\right\}\in \mathcal{K}.$$

抽象复形 $\mathcal{K}$ 的所有几何实现复形的伴随多面体都是分段线性同胚的, 因此之后我们不区分抽象复形和几何复形.

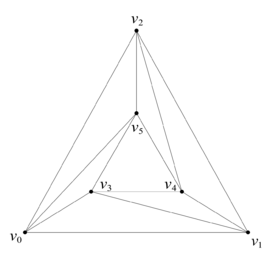
定理 1.2.6. 设 ${\mathcal{K}}^n$ 是 $n$ 维有限抽象复形, 它必可在 ${\mathbb{R}}^{2n+1}$ 上实现为几何复形.

证明. 考虑循环曲线$$\Phi :\mathbb{R}\to {\mathbb{R}}^{2n+1},t\mapsto (t,t^2,\dots ,t^{2n+1}),$$断言对于互不相同的 $t_0,\dots ,t_{2n+1}$, 有 $\Phi (t_0),\dots ,\Phi (t_{2n+1})$ 几何独立. 为此, 考虑$$\det [\Phi (t_1)-\Phi (t_0),\dots ,\Phi (t_{2n+1})-\Phi (t_0)]=\left|\begin{array}{ccc}{t}_1-t_0& \cdots & t_{2n+1}-t_0\\ ⋮& \ddots & ⋮\\ t_1^{2n+1}-t_0^{2n+1}& \cdots & t_{2n+1}^{2n+1}-t_0^{2n+1}\end{array}\right|\ne 0$$即得断言.

令 ${\mathcal{K}}^{(0)}=\left\{s_1,\dots ,s_N\right\}\setminus \left\{\varnothing \right\}$, 几何复形 $K$ 构造如下: $${\mathcal{K}}^0\ni s_i⟷\Phi (i)\in K^{(0)},$$则 $s=\left\{s_{i_1},\dots ,s_{i_p}\right\}\in \mathcal{K}$ 当且仅当 $(\Phi (i_1),\dots ,\Phi (i_p))\in K$, 其中 $p⩽n$. 下面证明如此构造的 $K$ 是一个几何复形, 定义的第一条显然满足, 只需证明任意两个单形的交或者非空, 或者是公共面即可.

任取 ${\sigma }^p,{\sigma }^q\in K$, 设它们有 $r$ 个公共顶点, 则 ${\sigma }^p$ 和 ${\sigma }^q$ 共有 $p+1+q+1-r$ 个不同的顶点, 而$$p+q+2-r⩽2n+2-r<2n+2,$$于是这些顶点几何独立, 它们确定了一个 $p+q+1-r$ 维单形 $\gamma$, 满足 ${\sigma }^p\prec \gamma$, ${\sigma }^q\prec \gamma$. 因此由单形的定义可知它们的交或者非空, 或者是公共面.

$\square$

推论 1.2.7. 设 $K$ 是有限复形, 且 $\dim K=n$, 则一定存在嵌入 $\left|K\right|\hookrightarrow {\mathbb{R}}^{2n+1}$.

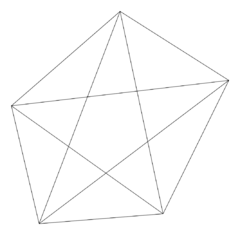
但是将上一推论的嵌入从 ${\mathbb{R}}^{2n+1}$ 改为 ${\mathbb{R}}^{2n}$ 后就不再成立了. 例如 $K_{{\sigma }^{2n+2}}^{(n)}$ 就不能嵌入 ${\mathbb{R}}^{2n}$. 最简单的情形, 令 $n=1$, 此时 $K_{{\sigma }^4}^{(1)}$ 即为下图:

图 3. $K_{{\sigma }^4}^{(1)}=K_{5,5}$

它就是完全图 $K_{5,5}$, 是一类不可平面化的图, 于是它不能嵌入 ${\mathbb{R}}^2$.

1.3单纯同调群

对复形的定向无非是对顶点的排序, 而排序本质上只有两种, 即由偶置换确定的同构类. 对 $\sigma$ 的顶点集 $\left\{v_0,\dots ,v_p\right\}$, 定义它在偶置换下的同构类为 $[v_0,\dots ,v_p]$, 就称它是复形 $\sigma$ 的一个定向.

特别地, 约定 $0$ 维情形下, $[a_0]$ 与 $-[a_0]$ 是两种不同的定向.

图 4. 低维复形的定向

定义 1.3.1 (定向复形). 称 $K$ 是一个定向复形, 若 $\forall \sigma \in K$, $\sigma$ 是有定向的. 并记$$S_p^{+}(K):=\left\{\sigma \in K:\dim \sigma =p\right\},S_p(K)=\left\{\pm \sigma :\sigma \in S_p^{+}(K)\right\}.$$

定理 1.3.2. 由 $S_p^{+}(K)$ 作为生成元可以生成一个自由 Abel 群, 记作$$C_p(K):=\left\{\sum _{\sigma \in S_p^{+}(K)}{n}_{\sigma }\sigma \right\},$$并要求求和为有限和.

证明. 考虑映射 $c_p:S_p(K)\to \mathbb{Z}$, 其中 $c_p$ 仅在 $S_p(K)$ 中有限个元素上取非零值, 且 $\forall \sigma \in S_p(K)$ 都有 $c_p(-\sigma )=-c_p(\sigma )$. 称 $c_p$ 是一个 $\mathbf{p}$–链. 取$$C_p(K)=\left\{c_p:S_p(K)\to \mathbb{Z}\right\},$$在它上面定义加法$$(c_p+c_p^{\prime })(\sigma ):=c_p(\sigma )+c_p^{\prime }(\sigma ),$$则 $(C_p(K),+)$ 是一个 Abel 群, 其中的零元 $0:S_p(K)\to \mathbb{Z}$, $\sigma \mapsto 0$, $c_p$ 的逆 $(-c_p)(\sigma ):=-c_p(\sigma )$.

接下来证明它是由 $S_p^{+}(K)$ 生成的自由 Abel 群. 我们需要做一点说明, 对 $\sigma \in S_p^{+}(K)$, 定义$$c_p^{\sigma }(\tau )=\{\begin{array}{ll}\pm 1,& \tau =\pm \sigma \\ 0,& \tau \ne \pm \sigma \end{array}$$则 ${\left\{c_p^{\sigma }\right\}}_{\sigma \in S_p^{+}(K)}$ 与 $S_p^{+}(K)$ 之间可以建立 1–1 对应, 于是可以用 $\sigma$ 替代 $c_p^{\sigma }$. $\forall c_p\in C_p(K)$, $\forall \sigma \in S_p^{+}(K)$, 记 $c_p(\sigma )=n_{\sigma }$, 那么构造的$$c_p^{\prime }=\sum _{\sigma \in S_p^{+}(K)}{n}_{\sigma }{c}_p^{\sigma }=\sum _{\sigma \in S_p^{+}(K)}{n}_{\sigma }\sigma$$自然是有限和. 断言 $c_p^{\prime }=c_p$.

为此, 对任意 $\tau \in S_p(K)$, 考虑$$c_p^{\prime }(\tau )=\sum _{\sigma \in S_p^{+}(K)}{n}_{\sigma }{c}_p^{\sigma }(\tau )\stackrel{\tau =\pm \sigma }{=}\pm n_{\sigma }=c_p(\pm \sigma )=c_p(\tau ).$$再说明唯一性, 令 $c_p=\sum _{\sigma \in S_p^{+}(K)}{n}_{\sigma }\sigma =\sum _{\sigma \in S_p^{+}(K)}{n}_{\sigma }^{\prime }\sigma$, 则$$\sum _{\sigma \in S_p^{+}(K)}(n_{\sigma }-n_{\sigma }^{\prime })\sigma =0_p.$$代入 $\tau =\pm \sigma$ 得到$$\sum _{\sigma \in S_p^{+}(K)}(n_{\sigma }-n_{\sigma }^{\prime })c_p^{\sigma }(\tau )=\pm (n_{\sigma }-n_{\sigma }^{\prime })=0_p(\tau )=0,$$即 $n_{\sigma }=n_{\sigma }^{\prime }$, 断言得证.

$\square$

图 5. 一个 $2$ 维定向复形的例子

考虑以上 $2$ 维复形的边界, 计算 $\partial [v_0,v_1,v_2]$ 得到$$\partial [v_0,v_1,v_2]=[v_0,v_1]+[v_1,v_2]+[v_2,v_0]=[v_0,v_1]-[v_0,v_2]+[v_1,v_2].$$并且注意到边界中的每一项符号与缺少的顶点标号有关.

图 6. 一个 $3$ 维定向复形的例子

再考虑 $3$ 维复形的边界: 这里所有 $2$ 维面的定向都使用右手法则来确定. 计算 $\partial [v_0,v_1,v_2,v_3]$ 得到$$\begin{array}{rl}\partial [v_0,v_1,v_2,v_3]& =[v_0,v_2,v_1]+[v_0,v_1,v_3]+[v_1,v_2,v_3]+[v_0,v_3,v_2]\\ & =-[v_0,v_1,v_2]+[v_0,v_1,v_3]-[v_0,v_2,v_3]+[v_1,v_2,v_3].\end{array}$$同样地, 注意到边界中的每一项符号都与缺少的顶点标号有关.

由此可以归纳得到, $$\partial [v_0,\dots ,v_p]=\sum _{k=0}^p(-1{)}^k[v_0,\dots ,{\hat{v}}_k,\dots ,v_p],$$其中 ${\hat{v}}_k$ 表示缺少这一项.

定义 1.3.3 (边缘算子). 称$$\partial :C_p(K)\to C_{p-1}(K),c_p=\sum _{\sigma \in S_p^{+}(K)}{n}_{\sigma }\sigma \mapsto \sum _{\sigma \in S_p^{+}(K)}{n}_{\sigma }\partial \sigma$$是 $C_p(K)$ 上的边缘算子, 有时为了强调也记作 ${\partial }_p$. 它是 $C_p(K)$ 到 $C_{p-1}(K)$ 的群同态, 其中 $\partial \sigma$ 如下定义: 对 $\sigma =[v_0,\dots ,v_p]$, 有$$\partial [v_0,\dots ,v_p]=\sum _{k=0}^p(-1{)}^k[v_0,\dots ,{\hat{v}}_k,\dots ,v_p].$$

命题 1.3.4. ${\partial }^2=0$. (严格地讲, 应该写成 ${\partial }_{p-1}{\partial }_p=0$)

证明. 任取 $\sigma =[v_0,\dots ,v_p]$, 计算$$\begin{array}{rl}{\partial }^2\sigma & =\partial \left(\sum _{k=0}^p(-1{)}^k[v_0,\dots ,{\hat{v}}_k,\dots ,v_p]\right)\\ & =\sum _{j<k}(-1{)}^k(-1{)}^j[\dots ,{\hat{v}}_j,\dots ,{\hat{v}}_k,\dots ]+\sum _{j>k}(-1{)}^k(-1{)}^{j-1}[\dots ,{\hat{v}}_k,\dots ,{\hat{v}}_j,\dots ]\\ & =\sum _{j<k}(-1{)}^{k+j}[\dots ,{\hat{v}}_j,\dots ,{\hat{v}}_k,\dots ]+\sum _{j<k}(-1{)}^{k+j-1}[\dots ,{\hat{v}}_j,\dots ,{\hat{v}}_k,\dots ]\\ & =0.\end{array}$$于是命题得证.

$\square$

定义 1.3.5 (同调群). 对链复形 $\mathcal{C}(K)=\left\{(C_p(K),{\partial }_p\right\}$, 对 ${\partial }_p:C_p(K)\to C_{p-1}(K)$, 称

1.	$Z_p(K):=\ker {\partial }_p=\left\{c_p\in C_p(K):\partial c_p=0\right\}$ 是 $K$ 的 $\mathbf{p}$ 维闭链群;
2.	$B_p(K):=\mathrm{im}{\partial }_{p+1}=\left\{\partial c_{p+1}\in C_p(K):c_{p+1}\in C_{p+1}(K)\right\}$ 是 $K$ 的 $\mathbf{p}$ 维边缘链群.

满足 $B_p(K)◃Z_p(K)$, 且 $B_p(K)$ 和 $Z_p(K)$ 仍是自由 Abel 群. 称$$H_p(K)=\ker {\partial }_p/\mathrm{im}{\partial }_{p+1}=Z_p(K)/B_p(K)$$是 $K$ 的 $\mathbf{p}$ 阶同调群.

在 $Z_p(K)$ 上可以定义等价关系: $$\begin{array}{rl}{z}_p\sim z_p^{\prime }& ⟺z_p+B_p(K)=z_p^{\prime }+B_p(K)\\ & ⟺z_p-z_p^{\prime }+B_p(K)=0⟺\exists d\in C_{p+1}(K)(\partial d=z_p-z_p^{\prime }),\end{array}$$这一等价关系称作同调关系, 确定的等价类 ${\bar{z}}_p$ 称作同调类. 它可以不局限于闭链群, 例如在 $C_p(K)$ 上同样可以定义$$c_p\sim c_p^{\prime }⟺\exists d\in C_{p+1}(K)(\partial d=c_p-c_p^{\prime }).$$特别地, 若 $\partial d=c_p$, 则 $c_p\sim 0$.

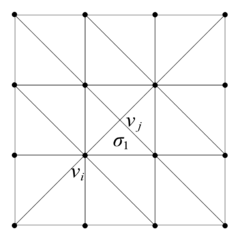
例 1.3.6. 考虑以下的 $2$ 维复形, 约定每一个 $2$ 维单形的定向都是逆时针.

取$$\begin{array}{rl}{z}_1& =[v_0,v_1]+[v_1,v_2]+[v_2,v_0]\in C_1(K)\\ z_2& =[v_3,v_4]+[v_4,v_5]+[v_5,v_3]\in C_1(K),\end{array}$$

计算可得$$\partial z_1=\partial z_2=0,$$于是 $z_1,z_2\in Z_1(K)$. 而$$\partial \left(\sum _{\sigma \in K^{(2)}\setminus K^{(1)}}\sigma \right)=z_1-z_2,$$于是由同调关系的定义可知 $z_1\sim z_2$.

将 ${\partial }_p$ 限制到 $\mathrm{im}{\partial }_p$ 上之后可知$${\partial }_p:C_p(K)\twoheadrightarrow \mathrm{im}{\partial }_p=B_{p-1}(K)$$是一个满同态. 于是由同态基本定理可知 $C_p(K)/\ker {\partial }_p\simeq \mathrm{im}{\partial }_p$. 

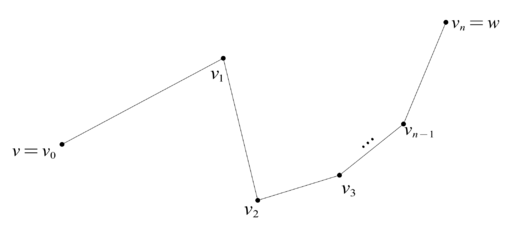
对复形 $K$, $v,w\in K^{(0)}$, 则 $v,w\in C_0(K)$. 于是由同调关系的定义可知$$v\sim w⟺\exists d\in C_1(K)(\partial d=w-v).$$在直观上, $v\sim w$ 即是存在一列 ${\left\{v_i\right\}}_{i=0}^n$ 满足 $v_0=v$, $v_n=w$ 使得 $v$ 与 $w$ 可以经由 $[v_i,v_{i+1}]$ 相连.

于是同调关系可以对 $K^{(0)}$ 分类, 以 $\bar{v}:=\left\{w\sim v:w\in K^{(0)}\right\}$ 记 $v$ 所在的等价类, 则$$K=\bigcup _{\bar{v}\in K^{(0)}/\sim }{K}_{\bar{v}}=\bigcup _{\bar{v}\in K^{(0)}/\sim }\left\{(v_0,\dots ,v_p)\in K:\left\{v_0,\dots ,v_p\right\}\subset \bar{v}\right\}.$$进一步, 其几何实现$$\left|K\right|=\bigcup _{\bar{v}\in K^{(0)}/\sim }\left|K_{\bar{v}}\right|,$$且 $\left|K_{\bar{v}}\right|$ 是道路连通的. 此时也称 $K_{\bar{v}}$ 是道路连通的.

定理 1.3.7. 对复形 $K$, $H_p(K)=\underset{\bar{v}\in K^{(0)}/\sim }{⨁}{H}_p(K_{\bar{v}})$, 即计算同调群只需分别计算各个道路连通分支的同调群即可.

证明. 首先 $C_p(K)=\underset{\bar{v}\in K^{(0)}/\sim }{⨁}{C}_p(K_{\bar{v}})$, 只需证明$$Z_p(K)=\underset{\bar{v}\in K^{(0)}/\sim }{⨁}{Z}_p(K_{\bar{v}}),B_p(K)=\underset{\bar{v}\in K^{(0)}/\sim }{⨁}{B}_p(K_{\bar{v}})$$即可. 注意到$$z_p\in Z_p(K)◃C_p(K)=\underset{\bar{v}\in K^{(0)}/\sim }{⨁}{C}_p(K_{\bar{v}}),$$这导出 $z_p=\sum _{\bar{v}\in K^{(0)}/\sim }{c}_p^{\bar{v}}$. 于是$$0=\partial z_p=\sum _{\bar{v}\in K^{(0)}/\sim }\partial c_p^{\bar{v}}$$导出 $\partial c_p^{\bar{v}}=0$. $B_p(K)$ 的情形类似可证.

$\square$

让我们做些计算! 设 $X$ 是一个拓扑空间, $H_0(X)$ 是其 $0$ 阶同调群. 取 $C_0(X)$, 它就是 $X$ 中点的形式和. 考虑边缘函数$$\partial :C_0(X)\to 0$$的核, $\ker \partial$ 即为整个空间 $C_0(X)$, 这意味着每一个点都是一个 “环”. 而 $[b]-[a]=0$ 当且仅当存在一个 $1$ 维链连结 $a$ 和 $b$, 于是这自然导向道路连通空间.

命题 1.3.8. 设 $K$ 是道路连通复形, 则 $H_0(K)=\mathbb{Z}$.

证明. 设 $v\in K^{(0)}$, 则 $\forall w\in K^{(0)}$, 因 $K$ 是道路连通的, 于是$$v\sim w⟺v+B_0(K)=\left\{v\right\}=\left\{w\right\}=w+B_0(K),$$则对任意 $\alpha =c_0+B_0(K)\in H_0(K)$, 都有$$c_0+B_0(K)=\sum _{v\in K^{(0)}}{n}_{v}v+B_0(K)\stackrel{\text{固定}{v}^{\prime }}{=}n{v}^{\prime }+B_0(K)=n\left\{v^{\prime }\right\},$$故 $H_0(K)={\mathbb{Z}}_{\left\{v^{\prime }\right\}}=\left\{n\left\{v^{\prime }\right\}:n\in \mathbb{Z}\right\}$. 断言 $\left\{v^{\prime }\right\}$ 是一个无限阶元.

为此, 令 $n\left\{v^{\prime }\right\}=0$, 也即 $n{v}^{\prime }+B_0(K)=0$, 则$$\exists c_1\in C_1(K)(\partial c_1=n{v}^{\prime }),$$另一方面$$c_1=\sum n_{ij}[v_i,v_j],\partial [v_i,v_j]=v_j-v_i,$$故 $\partial c_1=\sum _{v\in K^{(0)}}{n}_{v}v$ 中的系数和 $\sum _{v\in K^{(0)}}{n}_v=0$, 又由 $\partial c_1=\sum _{v\in K^{(0)}}{n}_{v}v=n{v}^{\prime }$ 可知$$n_v=\{\begin{array}{ll}n,& v=v^{\prime }\\ 0,& v\ne v^{\prime }\end{array}$$而系数和为零, 于是只能 $n=0$, 此即 $H_0(K)=\mathbb{Z}$.

$\square$

推论 1.3.9. $\left|K\right|$ 是道路连通的当且仅当 $H_0(K)=\mathbb{Z}$.

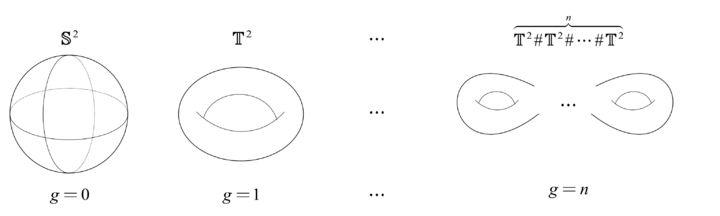
1.4$2$ 维闭曲面的同调群

例 1.4.1 ($2$ 维闭曲面的代数表示). $2$ 维闭曲面一共两类, 一类是可定向的:

图 7. 可定向的 $2$ 维闭曲面

 
其中 $♯$ 表示连通和. 它在两个流形中各挖去一个球, 并将球面边界粘贴在一起得到. 而不可定向的一类为$${\mathbb{RP}}^2,{\mathbb{RP}}^2♯{\mathbb{RP}}^2,\cdots ,{\mathbb{RP}}^2♯\cdots ♯{\mathbb{RP}}^2,\cdots ,$$其中 Klein 瓶实际上就是 ${\mathbb{RP}}^2♯{\mathbb{RP}}^2$. 由此, $2$ 维闭曲面的全体可以看作代数系$$⟨{\mathbb{S}}^2,{\mathbb{T}}^2,{\mathbb{RP}}^2;♯⟩.$$(当然, 这里需要证明 $♯$ 的确是一个代数运算. 首先对于可定向曲面, 亏格 $g$ 就是它的拓扑不变量. 对于不可定向曲面, 无论做了多少次连通和, 它永远可以通过连续变形构成一个定向曲面和一个 Möbius 带的形式.)

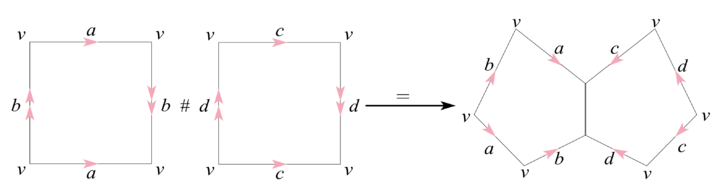
图 8. 一个 ${\mathbb{RP}}^2$ 和 ${\mathbb{RP}}^2$ 作连通和的例子

为了应用所谓的 push off 方法, 我们约定所有的 $2$ 维单形定向均为逆时针定向. 这有利于我们将复形推到它的边界上进行讨论.

引理 1.4.2. 设 $K$ 是一个闭曲面, 则

1.	对 $z_1\in Z_1(K)$, 存在 $z_1^{\prime }\in Z_1(\mathrm{Bd}K)$ 使得 $z_1\sim z_1^{\prime }$;
2.	对 $d\in Z_2(K)$ 使得 $\partial d\in C_1(\mathrm{Bd}K)$, 有 $d=l\left(\sum _{\dim \sigma =2}\sigma \right)$.

证明. (1) 因 $z_1\in Z_1(K)◃C_1(K)$, $z_1=\sum n_{ij}[v_i,v_j]$, 若一个非边界的 $[v_i,v_j]$ 使得 $n_{ij}\ne 0$, 则可以取到一个使得 $[v_i,v_j]$ 系数为负的 $2$ 维复形 ${\sigma }_1$:

此时$$\partial (n_{ij}{\sigma }_1)=n_{ij}\partial {\sigma }_1=-n_{ij}[v_i,v_j]+\cdots ,$$注意到取边界并不影响 $B_1(K)$, 于是$$z_1+B_1(K)=z_1+\partial (n_{ij}{\sigma }_1)+B_1(K)=\cdots =z_1^{\prime }+B_1(K)$$使得 $z_1\in Z_1(\mathrm{Bd}K)$.

(2) 由 $d\in Z_2(K)$ 可知$$d=\sum _{\dim \sigma =2}{n}_{\sigma }\sigma ,\partial d\in Z_1(\mathrm{Bd}K),$$由此, 考虑非边界上的 $1$ 维边, 如下图所示

 
于是对粉色边, 应当有 $n_{\sigma }=n_{{\sigma }^{\prime }}$, 再对蓝色边讨论, 有 $n_{{\sigma }^{\prime }}=n_{{\sigma }^{\prime \prime }}$, 由此进行下去可知 $d$ 中所有的 $n_{\sigma }$ 都相同.

$\square$

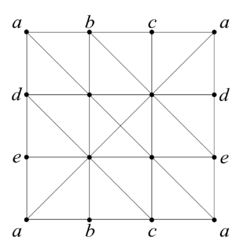
例 1.4.3 (${\mathbb{T}}^2$ 的同调群). 考虑 ${\mathbb{T}}^2$ 的三角剖分

对 $p<0$ 和 $p>2$ 自然有 $H_p({\mathbb{T}}^2)=0$.

因 ${\mathbb{T}}^2$ 道路连通, 由命题 1.3.8 可知 $H_0({\mathbb{T}}^2)=\mathbb{Z}$, 于是只需要计算 $H_1({\mathbb{T}}^2)$ 和 $H_2({\mathbb{T}}^2)$.

对 $\alpha \in H_1({\mathbb{T}}^2)$, 有$$\alpha =z_1+B_1(K)=\left\{z_1\right\},$$由引理 1.4.2 的 (1) 可知存在 $z_1^{\prime }\in Z_1(\mathrm{Bd}K)$ 使得 $z_1\sim z_1^{\prime }$. 而$$\mathrm{Bd}K=\left\{[a,b],[b,c],[c,a],[a,d],[d,e],[e,a]\right\}.$$设$$z_1^{\prime }=\sum _{i,j}{n}_{i,j}[i,j],$$令$$\begin{array}{rl}0& =\partial z_1^{\prime }\\ & =(-n_{ab}+n_{ca}-n_{ad}+n_{ea})a+(n_{ab}-b_{bc})b+(n_{bc}-n_{ca})c+(n_{ad}-n_{de})d+(n_{de}-n_{ea})e,\end{array}$$即$$n_{ab}=n_{bc}=n_{ca}=n,n_{ad}=n_{de}=n_{ea}=m.$$

为此, 记 $w=[a,b]+[b,c]+[c,a]$, $z=[a,d]+[d,e]+[e,a]$, 则$$\left\{z_1\right\}=\left\{z_1^{\prime }\right\}=\left\{nw+mz\right\}=nw+mz+B_1(K)=n\left\{w\right\}+m\left\{z\right\},$$故 $H_1({\mathbb{T}}^2)={\mathbb{Z}}_{\left\{w\right\}}+{\mathbb{Z}}_{\left\{z\right\}}$. 下面证明这一和为直和, 且 $\left\{w\right\}$ 和 $\left\{z\right\}$ 都是无限阶元.

令 $n\left\{w\right\}+m\left\{z\right\}=0$, 则$$\begin{array}{rl}nw+mz+B_1(K)=0& ⟺\exists d\in C_2(K)(\partial d=nw+mz\in Z_1(\mathrm{Bd}K))\\ & ⟹d=l\left(\sum _{\dim \sigma =2}\sigma \right).\end{array}$$其中第二行的推出由引理 1.4.2 的 (2) 得到. 此时 $\partial \left(\sum _{\dim \sigma =2}\sigma \right)=0$ (在三角剖分图中标注出定向即可看出), 即 $\partial d=0$, 从而 $nw+mz=0\in Z_1(\mathrm{Bd}K)$, 且 $n=m=0$. 故$$H_1({\mathbb{T}}^2)=\mathbb{Z}\oplus \mathbb{Z}.$$

再计算 $H_2({\mathbb{T}}^2)$, 注意到 $C_3({\mathbb{T}}^2)=0$, 故 $B_2({\mathbb{T}}^2)=0$, 故 $H_2({\mathbb{T}}^2)=Z_2({\mathbb{T}}^2)$. 对 $\alpha =z_2+B_2(K)=z_2\in Z_2({\mathbb{T}}^2)$, 有$$\begin{array}{rl}\partial z_2=0& ⟹\partial z_2\in Z_1(\mathrm{Bd}K)\\ & ⟹z_2=l\left(\sum _{\dim \sigma =2}\sigma \right)\\ & ⟹H_2({\mathbb{T}}^2)={\mathbb{Z}}_{\left(\sum _{\dim \sigma =2}\sigma \right)}\cong \mathbb{Z}.\end{array}$$同样地, 第二行的推出由引理 1.4.2 的 (2) 得到.

由此, 我们得到环面 ${\mathbb{T}}^2$ 的同调群如下: $$H_p({\mathbb{T}}^2)=\{\begin{array}{ll}\mathbb{Z},& p=0,2\\ \mathbb{Z}\oplus \mathbb{Z},& p=1\\ 0,& \text{其他}\end{array}$$

例 1.4.4 (Klein 瓶的同调群). Klein 瓶 $S$ 的三角剖分如下图所示:

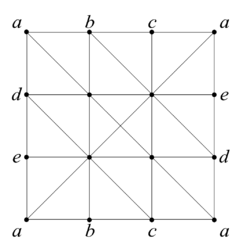
类似地记$$w=[a,b]+[b,c]+[c,a],z=[a,d]+[d,e]+[e,a],$$类似于 ${\mathbb{T}}^2$ 的计算方法, 对 $\left\{z_1\right\}=z_1+B_1(S)=z_1^{\prime }+B_1(S)$, 其中 $z_1^{\prime }\in Z_1(\mathrm{Bd}S)$, 有$$\left\{z_1^{\prime }\right\}=mw+nz+B_1(S)=m\left\{w\right\}+n\left\{z\right\},$$也即 $H_1(S)={\mathbb{Z}}_{\left\{w\right\}}+{\mathbb{Z}}_{\left\{z\right\}}$.

令 $m\left\{w\right\}+n\left\{z\right\}=0$, 则$$\begin{array}{rl}mw+nz+B_1(S)=0& ⟺\exists d\in C_2(S)(\partial d=mw+nz\in Z_1(S))\\ & ⟹d=l\left(\sum _{\dim \sigma =2}\sigma \right),\end{array}$$此时 $\partial d=2lz$, 记 $2lz=mw+nz=0$, 这意味着 $\left\{z\right\}$ 是 $2$ 阶元. 从而$$H_1(S)=\mathbb{Z}\oplus (\mathbb{Z}/2\mathbb{Z}).$$

$2$ 阶同调群的情形, 我们只需要注意到对唯一的 $2$ 维单形 $d$ 有 $\partial d\ne 0$ 即可得到 $H_2(S)=0$.

由此, 我们得到 Klein 瓶的同调群如下: $$H_p(S)=\{\begin{array}{ll}\mathbb{Z},& p=0\\ \mathbb{Z}\oplus (\mathbb{Z}/2\mathbb{Z}),& p=1\\ 0,& \text{其他}\end{array}$$

1.5约化同调

对单纯复形 $K$ 的链复形它有增广链复形为了使得 $\epsilon \circ \partial =0$, 只需要将 $v\in C_0(K)$ 映到 $\epsilon (v)=1$ 即可. 这由$$\epsilon \partial [v_1,v_0]=\epsilon (v_1)-\epsilon (v_0)=0$$即可验证. 而对抽象复形 $K$, 由于 $\left\{n\varnothing :n\in \mathbb{Z}\right\}=C_{-1}(K)\cong \mathbb{Z}$ 的存在, 它与几何复形的增广链复形相同.

定义 1.5.1 (约化同调). 称增广链复形导出的同调群 ${\tilde{H}}_i(K)$ 是约化同调群, 当 $i>0$ 时$${\tilde{H}}_i(K)=H_i(K),$$而 $i=0$ 时 ${\tilde{H}}_0(K)=\ker \epsilon /\mathrm{im}{\partial }_1$, 这里 $\ker \epsilon ⩽C_0(K)$.

命题 1.5.2. $H_0(K)\cong {\tilde{H}}_0(K)\oplus \mathbb{Z}$.

证明. 设 $K=\coprod _i{K}_i$, 其中 $K_i$ 是 $K$ 的道路连通分支. 任取 $v_i\in K_i^{(0)}$, 有$$H_0(K)\cong \underset{i}{⨁}{\mathbb{Z}}_{\left\{v_i\right\}}\cong \underset{i}{⨁}\mathbb{Z}.$$考虑约化同调群 ${\tilde{H}}_0(K)$, 设 $\left\{z_0\right\}=z_0+\mathrm{im}{\partial }_1\in {\tilde{H}}_0(K)$, 其中 $z_0\in \ker \epsilon$.

将 $z_0+\mathrm{im}{\partial }_1$ 在 $C_0(K)$ 中观察得到$$z_0+\mathrm{im}{\partial }_1=\sum _i{n}_i{v}_i+\mathrm{im}{\partial }_1,$$在 $\ker \epsilon$ 中观察, 得到$$0=\epsilon z_0=\sum _i{n}_i⟹n_0=-\sum _{i\ne 0}{n}_i,$$由此$${\tilde{H}}_0(K)=\underset{i\ne 0}{⨁}{\mathbb{Z}}_{\left\{v_i-v_0\right\}}.$$令 $\sum _{i\ne 0}{n}_i\left\{v_i-v_0\right\}=0\in {\tilde{H}}_0(K)$, 即 $\sum _{i\ne 0}{n}_i(v_i-v_0)+\mathrm{im}{\partial }_1$, 故存在 $d=\sum n_{uv}[u,v]\in C_1(K)$ 使得$$\sum n_{v}v=\sum _{i\ne 0}{n}_i(v_i-v_0).$$这里 $\sum n_v=0$, 因注意到 $\partial n_{uv}[u,v]=n_{uv}v-n_{uv}u$ 中点的系数总是一正一负交替出现, 比较上式两侧系数可知 $n_i=0$.

$\square$

定义 1.5.3 (锥). 设 $K$ 是一个复形, $v\in {\mathbb{R}}^{\mathbb{N}}$. 对任意 $\sigma =(v_0,\dots ,v_p)\in K$, 若 $v,v_0,\dots ,v_p$ 几何独立, 则它确定一个单形$$v\ast \sigma :=(v,v_0,\dots ,v_p),$$它的定向由 $[v,\sigma ]:=[v,v_0,\dots ,v_p]$ 确定. 由此得到一个复形$$v\ast K=K\cup \left\{v\right\}\cup \bigcup _{\sigma \in K}v\ast \sigma ,$$称作在 $v$ 处的锥.

图 9. 一个 $2$ 维复形 $K$ 与点 $v$ 形成的锥

从几何上来看, 容易得到 $\left|v\ast K\right|\cong \mathrm{pt}$.

引理 1.5.4. 设 $c$ 是 $K$ 的单形, 则$$\partial [v,c]=\{\begin{array}{ll}c-[v,\partial c],& \dim c>0\\ c-\epsilon (c)v,& \dim c=0\end{array}$$

证明. 计算 $v\ast K$ 的约化同调 ${\tilde{H}}_p(v\ast K)$, 考虑$$c_{p+1}=c_1+c_2\in C_{p+1}(K),c_1\in C_{p+1}(K),c_2=\sum _{\sigma \in K,\dim \sigma =p}{n}_{\sigma }(v\ast \sigma )=[v,\sum _{\sigma \in K,\dim \sigma =p}{n}_{\sigma }\sigma ].$$对 $p>0$, 有$$\begin{array}{rl}\partial [v,v_0,\dots ,v_p]& =[v_0,\dots ,v_p]+\sum _{i=0}^p(-1{)}^{i+1}[v,v_0,\dots ,{\hat{v}}_i,\dots ,v_p]\\ & =[v_0,\dots ,v_p]-\sum _{i=0}^p(-1{)}^i[v,v_0,\dots ,{\hat{v}}_i,\dots ,v_p]\\ & =[v_0,\dots ,v_p]-\left[v,\sum _{i=0}^p[v,v_0,\dots ,{\hat{v}}_i,\dots ,v_p]\right]\\ & =\sigma -[v,\partial \sigma ].\end{array}$$对 $p=0$, 有 $\partial [v,v_0]=v_0-v$.

$\square$

定理 1.5.5. 锥 $v\ast K$ 是零调的, 即 ${\tilde{H}}_p(v\ast K)=0$.

证明. 对 $p⩽0$ 和 $p>\dim K$, 显然 ${\tilde{H}}_p(K)=0$.

对 $1⩽p⩽\dim K$, 取 $z\in C_p(v\ast K)$ 满足 $\partial z=0$, 即 $z\in Z_p(v\ast K)$. 记 $z=c_1+c_2$, 其中 $c_1\in C_p(K)$ 被 $K$ 承载, $c_2=[v,c_2^{\prime }]$ 被 $v\ast K$ 承载. 计算$$0=\partial z=\partial c_1+\partial c_2=\partial c_1+\partial [v,c_2^{\prime }]=\{\begin{array}{ll}\partial c_1+c_2^{\prime }-[v,\partial c_2^{\prime }],& p>1\\ \partial c_1+c_2^{\prime }-\epsilon (c_2^{\prime })v,& p=1\end{array}$$即 $\partial c_1+c_2^{\prime }=0$, 且 $[v,\partial c_2^{\prime }]=0$, $\epsilon (c_2^{\prime })v=0$, 导出 $c_2^{\prime }=-\partial c_1$. 故$$z=c_1+[v,c_2^{\prime }]=c_1+[v,-\partial c_1]=c_1-[v,\partial c_1]=\partial [v,c_1]\in B_p(v\ast K).$$

从而 $Z_p(v\ast K)=B_p(v\ast K)$, 得到$${\tilde{H}}_p(v\ast K)=\frac{Z_p(v\ast K)}{B_p(v\ast K)}=0.$$$\square$

例 1.5.6 (${\mathbb{B}}^n$, ${\mathbb{S}}^n$ 的同调群). 我们需要承认同调群是拓扑不变量. 考虑 ${\mathbb{B}}^n\cong \left|K_{{\Delta }^n}\right|={\Delta }^n=(v_0,\dots ,v_n)$, 将 $K_{{\Delta }^n}$ 看作是 $\left|v_0\ast K_{(v_1,\dots ,v_n)}\right|$, 它是凸的. 于是 ${\tilde{H}}_p({\mathbb{B}}^n)=0$.

再考虑 ${\mathbb{S}}^n$ 的同调群: 因$${\mathbb{S}}^n=\left|\mathrm{Bd}{K}_{{\Delta }^{n+1}}\right|,{\mathbb{B}}^{n+1}=\left|K_{{\Delta }^{n+1}}\right|,\mathrm{Bd}{K}_{{\Delta }^{n+1}}=K_{\partial {\Delta }^{n+1}}=K_{{\Delta }^{n+1}}\setminus \left\{{\Delta }^{n+1}\right\},$$故 $C_{n+1}(K_{{\Delta }^{n+1}})\cong \mathbb{Z}$. 由此得链复形于是 $p\ne n$ 时有 ${\tilde{H}}_p({\mathbb{S}}^n)=H_p({\mathbb{B}}^{n+1})$, 当 $p=n$ 时有$$H_n({\mathbb{S}}^n)=H_n(K_{\partial {\Delta }^{n+1}})=\ker {\partial }_n=\mathrm{im}{\partial }_{n+1}=\left\{l\partial {\Delta }^{n+1}:l\in \mathbb{Z}\right\}\cong \mathbb{Z},$$而$$H_p({\mathbb{B}}^{n+1})=\frac{\ker {\partial }_p}{\mathrm{im}{\partial }_{p+1}}=0,$$于是$$H_p({\mathbb{S}}^n)=\{\begin{array}{ll}\mathbb{Z},& p=0,n\\ 0,& \text{其他}\end{array}$$

1.6单纯映射诱导的链映射

定义 1.6.1 ((诱导) 链映射). 设 $f:K\to L$ 是单纯映射, 则 $f:\sigma \mapsto f(\sigma )$ 诱导$$f_{♯}:C_p(K)\to C_p(L),\sigma =[v_0,\dots ,v_p]\mapsto f_{♯}(\sigma )=\{\begin{array}{ll}[f(v_0),\dots ,f(v_p)],& f(v_i)\text{两两不同}\\ 0,& \text{其他}\end{array}$$称 $f_{♯}$ 是 $f$ 诱导的链映射.

引理 1.6.2. 设 $f_{♯}$ 是 $f$ 诱导的链映射, 则对任何 $p\in \mathbb{Z}$, 交换.

证明. 即证对任意 $\sigma =[v_0,\dots ,v_p]$, 有 $\partial f_{♯}(\sigma )=f_{♯}(\partial \sigma )$. 由定义可知$$\partial f_{♯}(\sigma )=\{\begin{array}{ll}\tau =[f(v_0),\dots ,f(v_p)],& \dim \tau =p\\ 0,& \dim \tau <p\end{array}$$而$$f_{♯}(\partial \sigma )=f_{♯}\left(\sum _{i=0}^p(-1{)}^i[v_0,\dots ,{\hat{v}}_i,\dots ,v_p]\right)=\sum _{i=0}^p(-1{)}^i{f}_{♯}([v_0,\dots ,{\hat{v}}_i,\dots ,v_p]).$$当 $\dim \tau =p$ 时易知 $\partial f_{♯}(\sigma )=f_{♯}(\partial \sigma )$, 若 $\dim \tau <p$, 分两类情况讨论:

若 $\dim \tau ⩽p-2$, 则 $\left\{f(v_i)\right\}$ 中或者至少有三个相同, 或者至少有两对相同, 这意味着去掉一个顶点之后确定的 $f_{♯}([v_0,\dots ,{\hat{v}}_i,\dots ,v_p])=0$ 总是成立的. 此时 $\partial f_{♯}(\sigma )=f_{♯}(\partial \sigma )=0$.

若 $\dim \tau =p-1$, 不妨设 $f(v_0)=f(v_1)$, 此时 $\partial f_{♯}(\sigma )=0$, 而展开 $f_{♯}(\partial \sigma )$ 得到$$f_{♯}(\partial \sigma )=[f(v_1),f(v_2),\dots ,f(v_p)]-[f(v_0),f(v_2),\dots ,f(v_p)]=0.$$于是此时也有 $\partial f_{♯}(\sigma )=f_{♯}(\partial \sigma )=0$.

$\square$

命题 1.6.3. 对 $f_{♯}$, 它又可以诱导$$f_{\ast }:H_p(K)\to H_p(L),z_1+B_p(K)\mapsto f_{♯}(z_1)+B_p(K),$$且 $f_{♯}(Z_p(K))⩽Z_p(L)$, $f_{♯}(B_p(K))⩽B_p(L)$.

证明. 对任意 $z_p\in Z_p(K)$, 由$$\partial f_{♯}(z_p)=f_{♯}(\partial z_p)=f_{♯}(0)=0$$可知 $f_{♯}(z_p)\in Z_p(L)$; 对任意 $b_p\in B_p(K)$, 由 $\exists d\in C_{p+1}(K)$ 使得 $b_p=\partial d$, $$f_{♯}(b_p)=f_{♯}(\partial d)=\partial f_{♯}(d)$$可知 $f_{♯}(b_p)\in B_p(L)$.

$\square$

于是 $f\mapsto f_{\ast }$ 的确给出了从 $\mathsf{SimComp}$ 到 $\mathsf{Grp}$ 的一个函子: 只需要验证 $(gf{)}_{♯}=g_{♯}{f}_{♯}$ 即可. 对 $\sigma =[v_0,\dots ,v_p]$, 记 $\tau =[f(v_0),\dots ,f(v_p)]$, 则$$g_{♯}{f}_{♯}(\sigma )=\{\begin{array}{ll}{g}_{♯}(\tau ),& \dim \tau =p\\ 0,& \dim \tau <p\end{array}=\{\begin{array}{ll}[gf(v_0),\dots ,gf(v_p)],& \dim g_{♯}(\tau )=p\\ 0,& \dim g_{♯}(\tau )<p\end{array}=(gf{)}_{♯}(\sigma ).$$

推论 1.6.4. 若 $K,L$ 都是单纯复形, $K\cong L$, 则 $H_p(K)\cong H_p(L)$.

至此, 我们完成了的刻画.