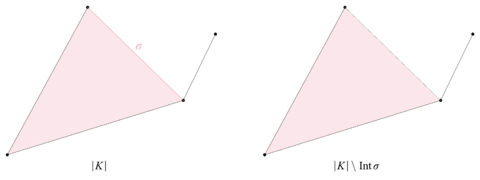单纯逼近定理 希望对拓扑空间 X , Y X ≅ Y H p ( X ) ≅ H p ( Y ) K X = ∣ K ∣ ∣ K ∣ ≅ ∣ L ∣ H p ( ∣ K ∣ ) ≅ H p ( ∣ L ∣ ) H p ( ∣ K ∣ )
对任何 ∣ K ∣ K ′ , K ′′ ∣ K ′ ∣ = ∣ K ′′ ∣ H p ( ∣ K ∣ ) = H p ( K )
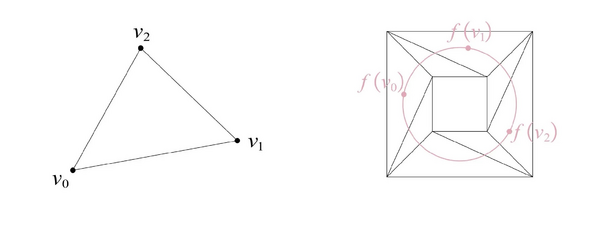
考虑 f ∈ C ( ∣ K ∣ , ∣ L ∣ ) g : K → L g ~ : ∣ K ∣ → ∣ L ∣ f = g ~ f
设 f : C ( ∣ K ∣ , ∣ L ∣ ) g f 单纯逼近 , 若对任意 x ∈ ∣ K ∣ ∃ ! σ ∈ K ( x ∈ Int σ ) ∧ ∃ τ ∈ L ( f ( x ) ∈ Int τ ∧ g ( x ) ∈ τ ) . f ( x ) g ( x ) L τ
设 g f ∈ C ( ∣ K ∣ , ∣ L ∣ ) g f ≃ g f f = g
证明. 由单纯映射的定义可知存在
τ ∈ L 使得
f ( x ) , g ( x ) ∈ τ , 而单形
τ 是一个凸集. 于是总存在同伦
H ( x , t ) = t f ( x ) + ( 1 − t ) g ( x ) . 任取
v ∈ K ( 0 ) , 因
f 被单纯映射诱导, 于是
f ( v ) ∈ L ( 0 ) . 而
g 是
f 的单纯逼近, 于是
∀ v ∈ K ( 0 ) ( f ( v ) = w = g ( v ) ∈ L ( 0 ) ) , 这即
f ∣ K ( 0 ) = g ∣ K ( 0 ) : K ( 0 ) → L ( 0 ) . 进而
f = g , 因从顶点出发可以一直诱导在高维骨架上的相等.
然而并不是所有的连续映射都存在单纯逼近, 考虑下面的例子: 设
K 的几何实现为
S 1 , 而
L 的几何实现是一个平环
{ z ∈ C : 1 ⩽ ∣ z ∣ ⩽ 2 } .
这因任何
K → L 的单纯映射必定落在
L 的一个
2 –单形中. 下面的问题就是: 在什么条件下存在单纯逼近?
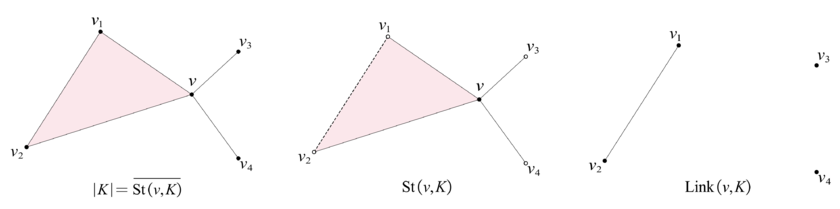
设 K v ∈ K ( 0 ) St ( v , K ) = σ ∈ K , v ∈ σ ⋃ Int σ , v K star . 并记Link ( v , K ) := St ( v , K ) ∖ St ( v , K ) = v ∗ τ ∈ K ⋃ τ , v K link .
证明. 这因
∣ K ∣ ∖ St ( v , K ) = σ ∈ K , v ∈ / σ ⋃ σ = L 是
∣ K ∣ 中的闭子集, 其中
L = { σ ∈ K : v ∈ / σ } 是
K 的子复形.
但
Int σ 在一般的情况下未必是
∣ K ∣ 中的开集.
图 1. 一个 Int σ ∣ K ∣ 而 link 就要更复杂一些, 下图给出了一个简单的
2 维复形中 link 的图示:
图 2. 一个 2 { v 0 , … , v p } ⊂ K ( 0 ) { v 0 , … , v p } i = 0 ⋂ p St ( v i , K ) = ∅
证明. 必要性. 取 σ = ( v 0 , … , v p ) ∈ K ( 0 ) ∀ i ∈ { 0 , … , p } Int σ ⊂ St ( v i , K ) ⟹ Int σ ⊂ i = 0 ⋂ n St ( v i , K ) , Int σ = ∅
充分性. 取
x ∈ i = 0 ⋂ p St ( v i , K ) ⊂ ∣ K ∣ = σ ∈ K ⋃ Int σ . 则存在
σ ∈ K 使得
x ∈ Int σ . 由 star 的定义,
v i 是
σ 的顶点, 即
v 0 , … , v p 是
σ 中的顶点.
设映射 f ∈ C ( ∣ K ∣ , ∣ L ∣ ) f star 条件 , 若∀ v ∈ K ( 0 ) ∃ w ∈ L ( 0 ) ( f ( St ( v , K )) ⊂ St ( w , L )) .
f ∈ C ( ∣ K ∣ , ∣ L ∣ ) g f v ∈ K ( 0 ) f ( St ( v , K )) ⊂ St ( g ( v ) , L ) .
证明. 必要性. 设 g : K → L f ∀ v ∈ K ( 0 ) ( f ( St ( v , K )) ⊂ St ( g ( v ) , L )) .
任取 x ∈ St ( v , K ) σ ∈ K x ∈ Int σ v ∈ σ g f τ ∈ L f ( x ) ∈ Int τ g ( x ) ∈ τ g g ( σ ) = τ 1 ∈ L g ( v ) ∈ g ( σ ) g ( x ) ∈ Int τ 1 σ = ( v 0 , … , v p ) x = i = 0 ∑ p t i v i ⟹ g ( x ) = i = 0 ∑ p t i g ( v i ) ∈ Int τ 1 , 即使 g ( v i ) 中有相等项也没有关系 ), 于是断言成立. 因 g ( x ) ∈ τ τ 1 ⊂ τ g ( v ) τ 1 τ
此时, f ( x ) ∈ Int τ ⊂ St ( g ( v ) , L ) f ( St ( v , K )) ⊂ St ( g ( v ) , L )
充分性. 假设 f g g : K ( 0 ) → L ( 0 ) , v ↦ g ( v ) = w f ( St ( v , K )) ⊂ St ( g ( v ) , L ) g
任取 σ = ( v 0 , … , v p ) ∈ K { g ( v 0 ) , … , g ( v p ) } L 2.1.5 知 i = 0 ⋂ p St ( v i , K ) = ∅ ∅ = f ( i = 0 ⋂ p St ( v i , K ) ) ⊂ i = 0 ⋂ p f ( St ( v i , K )) ⊂ i = 0 ⋂ p St ( g ( v i ) , L ) . 2.1.5 可知 { g ( v 0 ) , … , g ( v p ) } L τ =: g ( σ ) g
再证
g 是
f 的单纯逼近, 首先
∀ x ∈ ∣ K ∣ = σ ∈ K ⋃ Int σ ∃ ! σ = ( v 0 , … , v p ) ∈ K ∀ i ( x ∈ Int σ ⊂ St ( v i , K )) . 由题设和 star 的定义, 因
f ( x ) ∈ St ( g ( v i ) , L ) , 有
∃ τ ∈ L ( f ( x ) ∈ Int τ ) , 此时可知
g ( v i ) ∈ τ . 对
x = i = 0 ∑ p t i v i , 都有
g ( x ) = i = 0 ∑ p t i g ( v i ) ∈ τ . 故
g 是
f 的一个单纯逼近.
单纯逼近不能解决所有问题, 例如之前的例子
中
f 不存在单纯逼近. 此时就需要另外一种工具: 重分.
称 K ′ K 重分 , 若
1.
∀ τ ∈ K ′ ∃ σ ∈ K ( τ ⊂ σ )
2.
∀ σ ∈ K ∃ τ 1 , … , τ r ∈ K ′ ( σ = i = 1 ⋃ r τ i )
注意到在 R N ∣ K ′ ∣ = ∣ K ∣
f ∈ C ( ∣ K ∣ , ∣ L ∣ ) K K ′ f ∈ C ( ∣ K ′ ∣ , ∣ L ∣ ) g : K ′ → L
这是本节的中心定理, 我们只处理 K
任取 w ∈ K ( 0 ) v ∈ K St ( w , K ) ⊂ St ( v , K )
id : ∣ K ′ ∣ → ∣ K ∣ g : K ′ → K
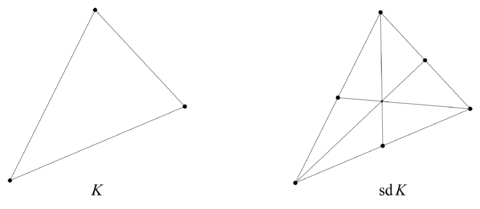
对 σ = ( v 0 , … , v p ) 重心 定义为σ ^ = p + 1 v 0 + ⋯ + v p . p = 0 K ( 0 ) L ( 0 ) = K ( 0 ) p = 1 K ( 1 ) L ( 1 ) = { σ ^ ∗ L σ : σ ∈ K ( 1 ) , dim σ = 1 , ∣ L σ ∣ = ∣ Bd σ ∣ } , p = k + 1 K ( k + 1 ) L ( k + 1 ) := { σ ^ ∗ L σ : σ ∈ K ( k + 1 ) , dim σ = k + 1 , L σ ⊂ L ( k ) ( ∣ L σ ∣ = ∣ Bd σ ∣ ) } , sd K = p ⩾ 0 ⋃ L ( p ) K 标准重心重分 . 类似地记 sd 2 = sd ( sd K )
图 3. 一个 2 也可以这样定义标准重心重分:
称 K σ 1 ⊂ σ 2 ⊂ ⋯ ⊂ σ r flag , 它确定单形 ( σ ^ 1 , … , σ ^ r ) 注意到它也可以唯一地确定 flag ), 定义sd K := { ( σ ^ 1 , … , σ ^ r ) : σ 1 ⊂ ⋯ ⊂ σ r } = { σ 1 ⊂ ⋯ ⊂ σ r } .
当 K K 网径 为mesh K := σ ∈ K max diam σ = σ ∈ K max x , y ∈ σ max ∥ x − y ∥ . v ∈ K ( 0 ) St ( v , K ) ⊂ B ( v , mesh K )
直观上, 标准重心重分减小了网径, 即 mesh sd K < mesh K
K mesh ( sd K ) ⩽ n + 1 n mesh K , m → ∞ mesh ( sd m K ) → 0
证明. 对 σ = ( v 0 , … , v p ) ∈ K diam σ = i , j max ∥ v i − v j ∥ ∀ x , y ∈ σ y = i = 0 ∑ p t i v i ∥ x − y ∥ ⩽ ∥ ∥ x − i = 0 ∑ p t i v i ∥ ∥ = ∥ ∥ i = 0 ∑ p t i ( x − v i ) ∥ ∥ ⩽ i max ∥ x − v i ∥ , ∥ v i − x ∥ ⩽ j max ∥ v i − v j ∥
任取
τ , σ ∈ sd K ,
τ ⊂ σ . 则
τ ⊂ σ ∈ K . 设
σ = ( v 0 , … , v p ) , 则存在
i 0 ∈ { 0 , … , p } 使得
∥ σ ^ − τ ^ ∥ ⩽ ∥ σ ^ − v i 0 ∥ = ∥ ∥ p + 1 1 i = 0 ∑ p v i − v i 0 ∥ ∥ = ∥ ∥ i = 0 ∑ p p + 1 v i − v i 0 ∥ ∥ ⩽ p + 1 p mesh K . 而
p ⩽ n 时总有
p / ( p + 1 ) ⩽ n / ( n + 1 ) . 得证.
现在我们回到单纯逼近定理 2.1.9 的证明:
定理 2.1.9 的证明. 若
K 是有限复形, 则
∣ K ∣ 一定是紧度量空间. 由 Lebesgue 覆盖引理可知对任何开覆盖
A , 都存在 Lebesgue 数
δ > 0 使得
∀ x ∈ ∣ K ∣ ∃ C ∈ A ( B ( x , δ ) ⊂ C ) . 对
f : ∣ K ∣ → ∣ L ∣ , 考虑
∣ L ∣ 的开覆盖
{ St ( w , L ) : w ∈ L ( 0 ) } , 存在
K 的开覆盖
A = { f − 1 ( St ( w , L )) : w ∈ L ( 0 ) } , 由 Lebesgue 覆盖引理, 存在
δ > 0 使得
∀ x ∈ ∣ K ∣ ∃ w ∈ L ( 0 ) ( B ( x , δ ) ⊂ f − 1 ( St ( w , L ))) . 由
2.1.14 可知存在正整数
m 使得
μ = mesh ( sd m K ) < δ . 任取
v ∈ ( sd m K ) ( 0 ) , 存在
w ∈ L ( 0 ) 使得
St ( v , sd m K ) ⊂ B ( v , μ ) ⊂ B ( v , δ ) ⊂ f − 1 ( St ( w , L )) . 也即
f ( St ( v , sd m K )) ⊂ St ( w , L ) . 这即 star 条件, 于是
f 存在单纯逼近
φ : sd m K → L .
链同伦 在上一小节我们知道了对复形进行适当次数的标准重心重分, 就可以得到连续映射的单纯逼近. 还有两个问题需要考虑: 其一是不同的单纯逼近是否诱导相同的同态 ; 其二是对不同的重分 K ′ , K ′′ , 它们的同调群 H p ( K ′ ) 和 H p ( K ′′ ) 之间是否存在同态 .
本小节主要来讨论第一个问题:
设 ψ , ψ ′ : C p ( K ) → C p ( L ) ψ ψ ′ 链同伦 , 若∃ D : C p ( K ) → C p + 1 ( L ) ( ∂ D + D ∂ = ψ − ψ ′ ) , ψ ≃ ψ ′
或者使用交换图的语言, 即图
φ , φ ′ : K → L f : ∣ K ∣ → ∣ L ∣ φ ♯ ≃ φ ♯ ′
证明. 任取 v ∈ K ′ ( 0 ) φ , φ ′ f f ( St ( v , K ′ )) ⊂ St ( φ ( v ) , L ) ∩ St ( φ ′ ( v ) , L ) . x ∈ K σ = ( v 0 , … , v p ) ∈ K ′ x ∈ Int σ τ ∈ L f ( x ) ∈ Int τ , φ ( x ) , φ ′ ( x ) ∈ τ . i ∈ { 0 , … , p } f ( x ) ∈ Int τ ⊂ f ( St ( v i ) , K ) ⊂ St ( φ ( v i ) , L ) ∩ St ( φ ′ ( v i ) , L ) , { φ ( v 0 ) , … , φ ( v p ) , φ ′ ( v 0 ) , … , φ ′ ( v p ) } L L ( σ ) dim L ( σ ) ⩽ 2 p + 1 , L ( σ ) L ( σ ) 这因 L ( σ ) 是单形生成的子复形 ), 而且对 s ⊂ σ L ( s ) ⊂ L ( σ ) 这只需注意到 L ( s ) ( 0 ) ⊂ L ( σ ) ( 0 ) φ ♯ ( σ ) φ ♯ ′ ( σ ) L ( σ )
(下面这一段证明的 pattern 非常重要, 这是一类基本技巧, 请务必掌握. ) 归纳地证明结论: 当 p = 0 v ∈ K ( 0 ) φ ♯ ( v ) = φ ( v ) φ ♯ ′ ( v ) = φ ′ ( v ) φ ♯ ( v ) , φ ♯ ′ ( v ) ∈ C 0 ( L ( v )) . L ( v ) φ ♯ ( v ) φ ♯ ′ ( v ) L ( v ) ∃ d ∈ C 1 ( L ( v )) ( ∂ d = φ ♯ ( v ) − φ ♯ ′ ( v )) , D ( v ) = d ∂ D 0 ( v ) + D − 1 ∂ v = ∂ D ( v ) = φ ♯ ( v ) − φ ♯ ′ ( v )
接下来设对任意 ⩽ p − 1 p σ ∈ K ′ dim σ = p ∂ D σ = φ ♯ ( σ ) − φ ♯ ′ ( σ ) − D ∂ σ c ∂ c = ∂ φ ♯ ( σ ) − ∂ φ ♯ ′ ( σ ) − ∂ D ( ∂ σ ) = ∂ φ ♯ ( σ ) − ∂ φ ♯ ′ ( σ ) − ( φ ♯ ( ∂ σ ) − φ ♯ ′ ( ∂ σ ) − D ∂ 2 σ ) = 0 , φ ♯ φ ♯ ′ ∂ { c } ∈ H p ( L ( σ )) c L ( σ ) 因每一项都被 L ( σ ) 承载 ). 故 { c } ∈ H p ( L ( σ )) = 0 c ∈ Z p ( L ( σ )) = B p ( L ( σ )) ∃ d ∈ C p + 1 ( L ( σ )) ( ∂ d = c ) , D ( σ ) = d
由此, 我们归纳地构造了
D 满足链同伦的条件, 从而
φ ♯ ≃ φ ♯ ′ .
设 φ , φ ′ : K → L f : ∣ K ∣ → ∣ L ∣ φ ∗ = φ ∗ ′
证明. 因对任意
z p + B p ( K ′ ) ∈ H p ( K ′ ) , 都有
φ ∗ ( z p + B p ( K ′ )) = φ ∗ ( z p ) + B p ( L ) = ∂ D ( z p ) + D ( ∂ z p ) + φ ∗ ′ ( z p ) + B p ( L ) = φ ∗ ′ ( z p ) + ∂ D ( z p ) + B p ( L ) = φ ∗ ′ ( z p ) + B p ( L ) 成立. 其中第二行的等号因
∂ z p = 0 , 第三行的等号因
D ( z p ) ∈ B p + 1 ( L ) 导出
∂ D ( z p ) ∈ B p ( L ) .
代数重分定理 本小节主要来讨论第二个问题: 即单纯逼近导出的同态是否依赖于对复形 K K ′ K id : ∣ K ′ ∣ → ∣ K ∣ g : K ′ → K g g ∗ g ∗ H p ( K ) H p ( L )
为此考虑这样的一类映射:
称 Φ : K → L , σ ↦ Φ ( σ ) = ∅ 零调承载子 , 若对任意 σ ∈ K Φ ( σ ) s ⊂ σ ⟹ Φ ( s ) ⊂ Φ ( σ ) .
设 f : C p ( K ) → C p ( L ) f Φ σ ∈ K dim σ = p f ( σ ) Φ ( σ )
Φ : K → L
1.
若 φ , ψ : C ( K ) → C ( L ) Φ D φ ≃ ψ
2.
存在被 Φ φ : C ( K ) → C ( L )
证明. (1) 无非就是 2.2.2 中使用相同的 pattern 证明, 只需要注意到 Φ ( σ ) 非空, 零调, 保持包含 ).
(2) 归纳地, p = 0 v ∈ K ( 0 ) ε ( v ) = 1 w Φ ( v ) φ 0 ( v ) = w 1 = ε ( v ) = ε ′ ( φ ( v )) = ε ′ ( w ) = 1 ,
当 p = 1 σ = [ v 0 , v 1 ] dim σ = 1 c = φ 0 ( ∂ σ ) ε ′ c = ε ′ φ 0 ( ∂ σ ) = ε ( ∂ σ ) = 0 , c { c } ∈ H ~ 0 ( Φ ( σ )) = 0 c ∈ ker ε ′ = im ∂ ⟹ ∃ d ∈ C 1 ( Φ ( σ )) ⊂ C 1 ( L ) ( ∂ d = c ) . φ 1 ( σ ) = d ∂ φ 1 ( σ ) = ∂ d = φ 0 ( ∂ σ ) C 1 ( K ) , C 0 ( K ) , C 1 ( L ) , C 0 ( L )
设 ⩽ p − 1 σ ∈ K dim σ ⩽ p − 1 φ Φ σ ∈ K dim σ = p ∂ φ ( ∂ σ ) = φ ∂ 2 σ = 0 , φ ( ∂ σ ) ∈ Z p ( Φ ( σ )) = B p ( Φ ( σ )) ⟹ ∃ d ∈ C p + 1 ( Φ ( σ )) ⊂ C p + 1 ( L ) ( ∂ d = φ ( ∂ σ )) . φ ( σ ) = d
现在提出本小节的中心定理:
K ′ K
1.
存在唯一的链映射 λ : C p ( K ) → C p ( K ′ ) λ ( σ ) K σ ′ λ 重分算子 .
2.
λ g ♯ g ∗ λ ∗
证明. 考虑Λ : K → K ′ , σ ↦ Λ ( σ ) = K σ ′ , K σ ′ Λ 2.3.2 可知存在唯一的 λ λ ( σ ) ∈ C ( Λ ( σ )) σ ∈ K Θ : K ′ → K , τ ↦ Θ ( τ ) = K σ τ , σ τ ∈ K τ K σ τ Θ 2.3.2 可知存在唯一的 θ θ ( τ ) ∈ C ( Θ ( τ )) τ ∈ K ′
同样地, 可以得到 id C ( K ) Ψ id C ( K ′ ) Φ
Claim 1. θ ∘ λ : C ( K ) → C ( K ) Ψ λ ∘ θ : C ( K ′ ) → C ( K ′ ) Φ
下面证明 Claim 1. 我们只说明 θ ∘ λ Ψ σ ∈ K λ ( σ ) Λ ( σ ) λ ( σ ) Λ ( σ ) = K σ ′ τ < σ θ ( τ ) Θ ( τ ) Θ ( τ ) = K σ τ = K σ = Ψ ( σ ) θ ∘ λ ( σ ) Ψ ( σ ) = K σ
Claim 2. Θ g ♯
下面证明 Claim 2. 任取 τ ∈ K ′ w ∈ τ Int τ ⊂ id ( St ( w , K )) ⊂ St ( g ( w ) , K ) , σ g ( w ) τ ⊂ σ σ τ ⊂ σ g ♯ Θ
由上述讨论, 仍有 g ♯ ∘ λ = id C ( K ) λ ∘ g ♯ = id C ( K ′ ) λ g ♯
接下来说明 λ λ ′ Λ 2.3.2 可知 λ ′ ≃ λ σ ∈ K dim σ = p ∂ D ( σ ) + D ( ∂ σ ) = λ ( σ ) − λ ′ ( σ ) . D : C p ( K ) → C p + 1 ( K ′ ) D ( σ ) Λ ( σ ) = K σ ′ K σ ′ p D ( σ ) = 0 ∀ σ ∈ K ( λ ( σ ) − λ ′ ( σ )) ⟹ λ = λ ′ .
最后, 我们来说明最开始假设 K σ ′ K ′ = sd K ∀ σ ∈ K ( K σ ′ = sd K σ = σ ^ ∗ L σ ) , ∣ L σ ∣ = ∣ Bd K σ ∣ H p ( K ) ≅ H p ( sd K ) K ′ = sd m K H p ( K ) ≅ H p ( sd K ) ≅ H p ( sd 2 K ) ≅ ⋯ ≅ H p ( sd m K ) . σ ∈ K 0 ≅ H ~ p ( sd K σ ) ≅ H ~ p ( sd m K σ ) sd m K σ K ′
再考虑任意的重分
K ′ , 考虑下图:
其中右侧映射是左侧 (
轴对称对应的 ) 单纯逼近. 那么由前面的讨论可知
( kh ) ∗ = k ∗ h ∗ 是同构, 这说明
h ∗ 是满同态; 类似地也有
( h l ) ∗ = h ∗ l ∗ 是同构, 这说明
h ∗ 是单同态. 故
h ∗ 是同构, 从而
k ∗ 也是同构. 于是得到
H ~ p ( K σ ′ ) ≅ H ~ p ( K σ ) = 0. 于是
K σ ′ 的确是零调的, 那么命题得证.
于是 f ∗ f ∗ K K K ′′ φ ′ : K ′′ → L φ ∗ g ∗ − 1 = φ ∗ ′ ( g ∗ ′ ) − 1
若 K ′′ K ′ id : ∣ K ′′ ∣ → ∣ K ′ ∣ k : K ′′ → K ′ ( g k ) ♯ ≃ g ♯ ′ , ( φ k ) ♯ ≃ φ ♯ ′ , ( g k ) ∗ = g ∗ ′ ( φ k ) ∗ = φ ∗ ′ φ ∗ ′ ( g ∗ ′ ) − 1 = φ ∗ k ∗ ( g ∗ k ∗ ) − 1 = φ ∗ g ∗ − 1 .
若 K ′′ K ′ 即重分是在 K 的每个单形中增加有限多个点 ), 那么总存在 K ′′′ K ′ K ′′ ( g k ) ∗ = ( g ′ k ′ ) ∗ , ( φ k ) ∗ = ( φ ′ k ′ ) ∗ , φ ∗ ′ ( g ∗ ′ ) − 1 = ( φ ′ k ′ ) ∗ ( g ′ k ′ ) ∗ − 1 = ( φ k ) ∗ ( g k ) ∗ − 1 = φ ∗ g ∗ − 1 .
同调群的同伦不变性 至此, 我们终于完成了以下函子的刻画:
证明. 为此只需验证 id : ∣ K ∣ → ∣ K ∣ id ∗ : H p ( K ) → H p ( K ) f : ∣ K ∣ → ∣ L ∣ h : ∣ L ∣ → ∣ M ∣ ( h f ) ∗ = h ∗ f ∗
其中第一条是显然的, 这里只证明第二条. 考虑以下的交换图:
则
h ∗ = φ ∗ g ∗ − 1 ,
f ∗ = ( g φ ′ ) ∗ ( g ∗ ′ ) − 1 , 计算得到
h ∗ f ∗ ( h f ) ∗ = φ ∗ g ∗ − 1 g ∗ φ ∗ ′ ( g ∗ ′ ) − 1 = ( φ φ ′ ) ∗ ( g ∗ ′ ) − 1 = φ ∗ φ ∗ ′ ( g ∗ ′ ) − 1 也即
( h f ) ∗ = h ∗ f ∗ .
证明. 对
∣ K ∣ ≅ ∣ L ∣ , 考虑
f : C ( ∣ K ∣ , ∣ L ∣ ) ,
h ∈ C ( ∣ L ∣ , ∣ K ∣ ) 使得
f h = id ∣ L ∣ ,
h f = id ∣ K ∣ . 由
2.4.1 可知
f ∗ h ∗ = ( f h ) ∗ = ( id ∣ L ∣ ) ∗ = id , h ∗ f ∗ = ( h f ) ∗ = ( id ∣ K ∣ ) ∗ = id , 也即
f ∗ 和
h ∗ 是同构, 得到
H p ( K ) ≅ H p ( L ) .
我们知道:K
设 f , g ∈ C ( ∣ K ∣ , ∣ L ∣ ) K f ≃ g f ∗ = g ∗
证明. 因 K H f g ∣ K ∣ × I ∣ K ∣ × I C = { H − 1 ( St ( w , L )) : w ∈ L ( 0 ) } , ∃ δ > 0 ∀ x ∈ ∣ K ∣ × I ∃ w ∈ L ( 0 ) ( B ( x , δ ) ⊂ H − 1 ( St ( w , L ))) . m ∈ Z ≥ 1 k > 0 v ∈ ( sd m K ) ( 0 ) St ( v , sd m K ) × [ k r − 1 , k r ] ⊂ B ( x , δ ) . w ∈ L ( 0 ) St ( v , sd m K ) × [ k r − 1 , k r ] ⊂ H − 1 ( St ( w , L )) . h ( r − 1 ) / k ( St ( v , sd m K )) ⊂ St ( w , L ) , h r / k ( St ( v , sd m K )) ⊂ St ( w , L ) . h ( r − 1 ) / k h r / k φ r : sd m K → L id : sd m K → K ∀1 ⩽ r ⩽ k ( h ( r − 1 ) / k ) ∗ = ( h r / k ) ∗ , f ∗ = ( h 0 ) ∗ = ( h 1/ k ) ∗ = ⋯ = ( h ( k − 1 ) / k ) ∗ = ( h 1 ) ∗ = g ∗ . □
若 ∣ K ∣ ≃ ∣ L ∣ H p ( ∣ K ∣ ) ≅ H p ( ∣ L ∣ )
证明. 这即存在
f ∈ C ( ∣ K ∣ , ∣ L ∣ ) ,
g ∈ C ( ∣ L ∣ , ∣ K ∣ ) 使得
f g ≃ id ∣ L ∣ , g f ≃ id ∣ K ∣ , 由此
f ∗ 与
g ∗ 互逆. 即
H p ( ∣ K ∣ ) ≅ H p ( ∣ L ∣ ) .
应用: 映射度, Brouwer 不动点定理 考虑到 S 0 n > 0
设 f ∈ C ( S n , S n ) f ∗ : H n ( S n ) → H n ( S n ) , α ↦ f ∗ ( α ) = d α , d ∈ Z . α S n d f 映射度 , 记作 deg f
当 n = 1 deg f deg f f π 1 ( S 1 ) = [ S 1 , S 1 ] → Z f ↦ deg f S 1
f , g : S n → S n
1.
若 f ≃ g deg f = deg g
2.
deg ( g f ) = deg f ⋅ deg g
3.
deg id = 1 c deg c = 0
证明. (2) 因
deg ( g f ) α = ( g f ) ∗ α = g ∗ ( deg f α ) = deg f ⋅ g ∗ α = deg f ⋅ deg g α . 而 (1), (3) 是显然的.
F ∈ C ( D n + 1 , S n ) deg ( F ∣ ∂ D n + 1 ) = 0
证明. 这因
且
F ∣ ∂ D n + 1 = F ∘ ι . 由
H n ( D n + 1 ) = 0 可知
( F ∣ ∂ D n + 1 ) ∗ = 0 .
不存在这样的 r ∈ C ( D n + 1 , S n ) r ∣ ∂ D n + 1 = id S n
证明. 由
2.5.3 可知若存在这样的
r , 有
deg ( r ∣ ∂ D n + 1 ) = 0 . 再由
2.5.2 可知
deg ( id S n ) = 1 , 矛盾.
证明. 用反证法, 任取
x ∈ D n , 都有
f ( x ) = x . 取
h : D n → S n + 1 , x ↦ ∥ x − f ( x ) ∥ x − f ( x ) . 由
2.5.3 可知
deg ( h ∣ ∂ D n ) = 0 , 作同伦
H : S n − 1 × I → S n − 1 , ( x , t ) ↦ ∥ x − t f ( x ) ∥ x − t f ( x ) . 这一同伦的定义是合理的, 因
x = f ( x ) 可知
t = 1 时
x − f ( x ) = 0 , 而
0 ⩽ t < 1 时若有
x = t f ( x ) , 则
1 = ∥ x ∥ = ∥ t f ( x ) ∥ = t ∥ f ( x ) ∥ ⩽ t < 1 , 矛盾. 此时
H ( x , 0 ) = id S n − 1 ( x ) , H ( x , 1 ) = h ∣ ∂ D n ( x ) , 即
id S n − 1 ≃ h ∣ ∂ D n , 而它们的映射度不相等, 矛盾.
Brouwer 不动点定理在 n = 1 n = 2 n ⩾ 1
接下来考虑从球面到球面的映射, f ∈ C ( S n , S n ) 对径映射 r : x ↦ − x
证明. 考虑 r i : S n → S n i ( x 1 , … , x i , … , x n + 1 ) ↦ ( x 1 , … , − x i , … , x n + 1 ) . r = r n + 1 r n ⋯ r 1 deg r = i = 1 ∏ n + 1 deg r i r n + 1 = h i , n + 1 r i h i , n + 1 − 1 deg r n + 1 = deg h i , n + 1 deg r i deg h i , n + 1 − 1 = deg r i . deg r = ( deg r n + 1 ) n + 1
考虑
S n 的如下三角剖分:
它由
R n + 1 上典范正交基的顶点
{ ± e 1 , ± e 2 , … , ± e n + 1 } 确定. 记
e − i = − e i , 得到复形
K ∣ K ∣ = { ( x 1 , … , x n + 1 ) ∈ R n + 1 : i = 1 ∑ n + 1 ∣ x i ∣ = 1 } . 考虑中心辐射
φ : ∣ K ∣ → S n , 有
那么对
K 中的
n 维单形, 给定如下的定向: (
约定 i j = ± j )
± [ e i 1 , e i 2 , … , e i n + 1 ] { 取 + ⟺ { i k } 中有偶数个负数 取 − ⟺ { i k } 中有奇数个负数 令
z n = σ ∈ S + n ( K ) ∑ σ 可知
∂ z n = 0 . 这里
S + n ( K ) 是
K 中正定向
n 维单形全体. 此时
z n ∈ Z n ( K ) = H n ( S n ) , 那么
( r ~ n + 1 ) ♯ : C n ( K ) → C n ( K ) , ± [ e 1 , … , e n + 1 ] ↦ ∓ [ e 1 , … , e n + 1 ] . 故
( r ~ n + 1 ) ♯ ( z n ) = − z n , 由此
deg r ~ n + 1 = − 1 得到
deg r n + 1 = − 1 .
h ∈ C ( S n , S n ) deg h = ( − 1 ) n + 1 h
证明. 用反证法, 设
∀ x ∈ S n ( h ( x ) = x ) . 取
H : S n × I → S n , ( x , t ) ↦ ∥ ( 1 − t ) h ( x ) + t ( − x ) ∥ ( 1 − t ) h ( x ) + t ( − x ) . 类似地, 若有
( 1 − t ) h ( x ) − t x = 0 , 则
∥ ( 1 − t ) h ( x ) ∥ = t ∥ x ∥ ⟹ 1 − t = t ⟹ t = 2 1 . 而将
t = 1/2 代入之后有
1/2 ( h ( x ) − x ) = 0 , 于是
H 是合理定义的. 此时由
H ( x , 0 ) = h ( x ) , H ( x , 1 ) = r ( x ) 可知
h ≃ r , 而
deg h = deg r = ( − 1 ) n + 1 , 矛盾.
f ∈ C ( S n , S n ) deg f = 1 x 0 ∈ S n f ( x 0 ) = − x 0
证明. 考虑
r f : S n → S n , 有
deg ( r f ) = ( − 1 ) n + 1 . 由
2.5.7 可知
r f 存在不动点
x 0 , 那么
r f ( x 0 ) = x 0 ⟹ − f ( x 0 ) = x 0 , 于是命题得证.
下面把这一问题应用于所谓的 “毛球问题”:
称 v : X → R n X 向量场 (当 n = 1 数量场 ). 特别地, v : S n → R n + 1 x ∈ S n ⟨ x , v ( x ) ⟩ = 0
S n 向量场非零指它在任何一点都非零. ) 当且仅当 n
证明. 充分性. 因 n = 2 k − 1 v : S n → S n , ( x 1 , x 2 , … , x 2 k − 1 , x 2 k ) ↦ ( − x 2 , x 1 , … , − x 2 k , x 2 k − 1 )
必要性. 若
S n 存在非零切向量场
v , 考虑它诱导的映射
h : S n → S n , x ↦ ∥ v ( x ) ∥ v ( x ) , 因
v 是切向量场, 故
h 也是切向量场, 于是
∀ x ∈ S n ( h ( x ) = x ∧ h ( x ) = − x ) . 由
2.5.7 可知
deg h = ( − 1 ) n + 1 , 又由
2.5.8 可知
deg h = 1 , 于是
n 是奇数.
应用: Euler 示性数, Lefschetz 不动点定理 设 K H p ( K ) = ker ∂ p / im ∂ p + 1 G G ≅ Z ⊕ Z ⊕ ⋯ ⊕ Z ⊕ ( Z / t 1 Z ) ⊕ ( Z / t 2 Z ) ⊕ ⋯ ⊕ ( Z / t k Z ) = F ( G ) ⊕ T ( G ) , F ( G ) G r T ( G ) G t 1 ∣ t 2 ∣ ⋯ ∣ t k H i ( K ) β 1 ( K ) := rank F ( H i ( K )) K i Betti 数 .
我们把 Brouwer 定理再次推广, 不仅仅考虑球面之间的映射, 而考虑一般的复形 K f ∈ C ( ∣ K ∣ , ∣ K ∣ )
设 φ : V → V { e 1 , … , e n } V φ { e i } A tr φ := tr A φ 迹 .
W V φ φ ( W ) ⊂ W φ φ ∗ : V / W → V / W , x + W ↦ φ ( x ) + W , tr φ = tr ( φ ∣ W ) + tr φ ∗ .
证明. 设
W 有一组基
{ ξ 1 , … , ξ r } ,
V 的基
{ ξ 1 , … , ξ r , ξ r + 1 , … , ξ n } 由
W 的基扩张而来, 则
V / W 以
{ ξ r + 1 + W , … , ξ n + W } 为一组基. 设
φ ,
φ ∣ W 和
φ ∗ 在对应基下的矩阵分别为
A , A W , A ∗ , 则
A = [ A W ∗ A ∗ ] , 这导出
tr φ = tr ( φ ∣ W ) + tr φ ∗ .
设 G φ : G → G tr φ G φ H φ φ ∗ : G / H → G / H , G / H tr φ = tr ( φ ∣ H ) + tr φ ∗
为了记号方便, 我们约定将链群、闭链群、边缘链群中的复形记号省略掉, 并且记H p = Z p / B p = T p ⊕ F p , T p H p F p H p Z p B p W p := { c p ∈ C p : ∃ ℓ ∈ Z ∖ { 0 } ( ℓ c p ∈ B p ) } . B p
设 φ : C ( K ) → C ( K ) K p ∑ ( − 1 ) p tr φ ∣ C p = p ∑ ( − 1 ) p tr ( φ ∗ , H p / T p ) , φ ∗ 因形如 Z / m Z → Z 的同态必为零同态, 于是一定 φ ( T p ) ⩽ T p . )
证明. 根据前面约定的记号, 容易得到B p ⩽ W p ⩽ Z p ⩽ C p .
首先考虑 Z p ⩽ C p C p ↠ ∂ p B p − 1 ⩽ C p − 1 Z p = ker ∂ p C p / Z p ≅ B p − 1 . B p − 1 C p / Z p 2.6.2 可知tr ( φ ∣ C p ) = tr ( φ ∣ Z p ) + tr ( φ ∗ , C p / Z p ) = tr ( φ ∣ Z p ) + tr ( φ ∗ , B p − 1 ) .
再考虑 W p ⩽ Z p z p ∈ W p j ( z p ) = { z p } + T p W p ℓ ∈ Z ∖ { 0 } ℓ z p ∈ B p ℓ { z p } + T p = { ℓ z p } + T p = 0 + T p , W p ⩽ ker j z p ∈ ker j j ( z p ) = { z p } + T p = 0 ⟹ ∃ ℓ ∈ Z ∖ { 0 } ( ℓ { z p } = 0 ) ⟹ z p ∈ W p ker j ⊂ W p W p = ker j Z p / W p ≅ H p / T p = F p . F p Z p / W p 2.6.2 可知tr ( φ ∣ Z p ) = tr ( φ ∣ W p ) + tr ( φ ∗ , Z p / W p ) = tr ( φ ∣ W p ) + tr ( φ ∗ , F p ) .
最后, 考虑 B p ⩽ W p rank B p = rank W p tr ( φ ∣ B p ) = tr ( φ ∣ W p ) m = rank B p < rank W p = r
设 { α 1 , … , α r } W p n i ∈ Z ≥ 1 { n 1 α 1 , … , n m α m } B p r > m n m + 1 ∈ Z ≥ 1 n m + 1 α m + 1 ∈ B p 这由 W p 的定义可得 ), 矛盾, 于是 r = m
设 φ ∣ W p { α 1 , … , α r } A = [ a ij ] φ ∣ B p { n 1 α 1 , … , n r α r } B = [ b ij ] φ ∣ W p ( α j ) = i = 1 ∑ r a ij α i ⟹ φ ∣ W p ( n j α j ) = i = 1 ∑ r a ij n j α i . φ ∣ B p ( n j α j ) = i = 1 ∑ r b ij n i α i . B p ⩽ W p i = 1 ∑ r a ij n j α i = i = 1 ∑ r b ij n i α i i , j a ij n j = b ij n i . i = j a ii = b ii tr ( φ ∣ W p ) = tr A = i = 1 ∑ r a ii = i = 1 ∑ r b ii = tr B = tr ( φ ∣ B p ) .
于是:
tr ( φ ∣ C p ) = tr ( φ ∣ Z p ) + tr ( φ ∣ B p − 1 ) = tr ( φ ∣ W p ) + tr ( φ ∗ , F p ) + tr ( φ ∣ B p − 1 ) = tr ( φ ∣ B p ) + tr ( φ ∣ B p − 1 ) + tr ( φ ∗ , F p ) . 因
K 是有限复形, 于是下面的交错和是有限和, 得到
p ⩾ 0 ∑ ( − 1 ) p tr ( φ ∣ C p ) = p ⩾ 0 ∑ ( − 1 ) p tr ( φ ∣ B p ) − ( − 1 ) p − 1 tr ( φ ∣ B p − 1 ) + ( − 1 ) p tr ( φ ∗ , F p ) = p ⩾ 0 ∑ ( − 1 ) p tr ( φ ∗ , F p ) . 于是定理成立.
我们再进一步讨论一下这些子群: 由 Z p / W p ≅ H p / T p Z p = W p ⊕ A W p / B p ≅ T p B p Z p ≅ B p W p ⊕ A ≅ B p W p ⊕ A ≅ T p ⊕ A , A ≅ F p
设 K h : ∣ K ∣ → ∣ K ∣ Λ ( h ) := p ∑ ( − 1 ) p tr ( h ∗ , H p / T p ) h Lefschetz 数 .
由定义可知若 h ≃ h ′ Λ ( h ) = Λ ( h ′ ) h ∗ = h ∗ ′ Λ ( h ) ∣ K ∣
特别地, 若允许同调群中的系数在数域中取值, 那么 C p H p K p dim F H p = β p ( K )
考虑 id : ∣ K ∣ → ∣ K ∣ Λ ( id ) = p ⩾ 0 ∑ ( − 1 ) p tr ( id ∗ , H p / T p ) = p ⩾ 0 ∑ ( − 1 ) p β p ( K ) . K p f p f ( K ) = ( f 0 , … , f n ) rank C p ( K ) = f p = β p ( K ) . χ ( K ) = p ⩾ 0 ∑ ( − 1 ) p rank C p ( K ) K Euler 示性数 .
Euler 示性数是拓扑不变量, 它与 ∣ K ∣ χ ( ∣ K ∣ ) = p ⩾ 0 ∑ ( − 1 ) p β p ( K ) .
一些典型的曲面 Euler 示性数可以计算出来:χ ( T 2 ) = 0 , χ ( S ) = 0 , χ ( RP 2 ) = 1 , χ ( S n ) = { 2 , 0 , n = 2 k n = 2 k + 1 .
K h ∈ C ( ∣ K ∣ , ∣ K ∣ ) Λ ( h ) = 0 h
证明. 用反证法, 设 ∀ x ∈ ∣ K ∣ ( h ( x ) = x ) f : ∣ K ∣ → R , x ↦ ∥ x − h ( x ) ∥ , ∣ K ∣ ε mesh K < ε /2 否则取足够多次数的标准重心重分 ).
记 h : ∣ K ∣ → ∣ K ∣ φ : sd m K → K x ∈ K h ( x ) φ ( x ) K ∥ h ( x ) − φ ( x ) ∥ ⩽ mesh K < 2 ε , ∥ x − φ ( x ) ∥ ⩾ ∥ x − h ( x ) ∥ − ∥ h ( x ) − φ ( x ) ∥ > 2 ε .
由代数重分定理:
则
h ∗ = ( φ ♯ λ ) ∗ = ξ ∗ . 故
Λ ( h ) = p ⩾ 0 ∑ ( − 1 ) p tr ( h ∗ : H p / T p ) = p ⩾ 0 ∑ ( − 1 ) p tr ( ξ ∗ , C p ) . 我们断言
tr ( ξ ∗ , C p ) = 0 . 这蕴含着
ξ p 在
S p + ( K ) (
K 的定向 p 维单形全体, 这是 C p ( K ) 的一组基 ) 下的矩阵
A 满足
tr A = 0 . 这意味着
ξ p ( σ ) 中不能含有
σ . 因
λ ( σ ) 被
sd m K σ 承载, 若
ξ p ( σ ) = φ ♯ λ ( σ ) = aσ + ⋯ , a = 0 , 在
λ ( σ ) 的展开式中应当存在
p 维单形
τ ∈ sd m K σ 使得
φ ♯ ( τ ) = a ′ σ + ⋯ , a ′ = 0. 因对任意
x ∈ τ 都有
φ ( x ) ∈ σ , 又
τ ⊂ σ , 故
x ∈ σ , 从而
2 ε < ∥ x − φ ( x ) ∥ ⩽ mesh K < 2 ε , 矛盾.
S n deg r = ( − 1 ) n + 1
证明. 由
2.6.6 知
Λ ( r ) = 1 + ( − 1 ) n deg r = 0 .
设 K f ∈ C ( ∣ K ∣ , ∣ K ∣ )
证明. 设 f ∗ : H 0 ( K ) → H 0 ( K ) φ : K ′ → K
对
v ∈ K ( 0 ) ,
K v ′ = { v } , 有
λ ( v ) = ℓ v . 由
1 = ε ( v ) = ε ′ λ ( v ) = ℓ ε ′ ( v ) = ℓ 可知
λ ( v ) = v , 于是
φ ♯ ( λ ( v )) = φ ♯ ( v ) = φ ( v ) 与
v 在同一同调类中, 这即
f ∗ ( { v } ) = { φ ∗ ( λ ( v )) } = { v } , 即
f ∗ = id ∗ . 故
Λ ( f ) = Λ ( id ) = 1 = 0 . 由
2.6.6 得证.
设 χ ( ∣ K ∣ ) = 0 id ∣ K ∣ f ∈ C ( ∣ K ∣ , ∣ K ∣ ) f
证明. 因
Λ ( f ) = Λ ( id ) = χ ( ∣ K ∣ ) = 0 .