1.3. 应用: 三等分已知角
给定 的子集 , 由 中两点 所决定的直线被称为 -直线; 以 中某点 为圆心、以 为半径所作的圆, 其中 , 被称为 -圆.
定义 1.3.1 (尺规可作性). 给定 , 如果点 满足如下三个条件之一:
• | 是两条 -直线的唯一交点; |
• | 是一条 -直线和一个 -圆的交点; |
• | 是两个 -圆的交点; |
就称 是 -直接可作的. 假设存在有限个点 , 使得对任意的 , 是 -直接可作的并且 , 就称 是 -可作的.
令 . 如果 是某个 -可作点的横坐标或者纵坐标, 我们就称实数 是尺规可作的或者可作的.
中尺规可作的数满足如下三条性质:
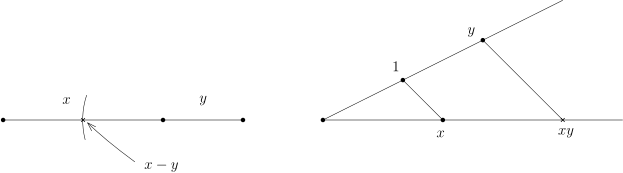
1) | 若 是可作的, 则 和 可作. 通过以下图示可以看出: 其中, 右图中需要做过 点的平行线. |
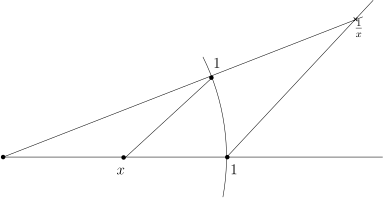
2) | 若 是可作的并且 , 则 可作. 根据 1), 只要按照上图的方式做出 即可. |
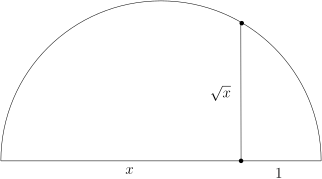
3) | 若 是可作的, 则 也可作. |
注记 1.3.2. 从 出发, 根据前两条, 中的数是尺规可作的.
注记 1.3.3. 前两条表明尺规可作的数构成一个域. 这是 的一个中间域.
定理 1.3.4 (Wantzel, 1937). 是尺规可作的当且仅当存在有限个域扩张使得 () 并且 .
特别地, 如果 是尺规可作的, 必存在 , 使得 并且 是 的幂.
引理 1.3.5. 给定域扩张 , . 那么, 存在 , 但是 , 使得 是 的基.
证明. 给定 , 假设 中所有点的横纵坐标都落在域 中. 我们首先证明, 如果 是 -直接可作的, 令 , 那么 . 注意到, 我们可以把 -直线和 -圆写成以 的数为系数的方程的零点.
1) | 若 是两条 -直线的交点, 通过解两个 -系数的线性方程联立所得到的方程组, 其横纵坐标 和 仍是 中的数, 从而 , 即 . |
2) | 如果 是 -直线和 -圆的交点. 此时, 需要解一个 -系数的线性方程和一个 -系数的二次方程的联立, 可以通过先用线性方程代换掉一个变量, 从而解一个一元二次方程来求得 或者 . 根据二次方程的求根公式, 可以通过 添加该一元二次方程的判别式的平方根得到, 即 , 从而, 张成了 . 特别地, . |
3) | 如果 是两个 -圆的交点, 它们对应的圆方程的二次项形如 . 通过相减, 就可以得到一个一次方程, 这就化为前一情形. |
从 出发, 通过有限步得到 , 上面的讨论表明每次添加新得到的数得到的域, 如果与之前不同的话, 扩张的次数必为 . 据此, 我们得到其中, , .
推论 1.3.6 (倍立方问题). 不是尺规可作的.
另一个著名的古典几何问题是研究是否可用尺规作出大小为给定角的三分之一的角?
推论 1.3.7 (三等分已知角). 不是尺规可作的. 特别地, 不能通过尺规作图三等分 的角.
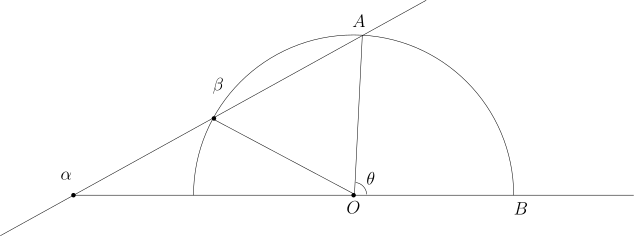
注记 1.3.8. 通过升级的直尺和圆规, 我们可以三等分已知角. 最著名的例子是 Archimedes 的 “二刻度尺”. 所谓的二刻度尺就是在一个直尺上标记了两个点 和 .
给定角度 , 我们做以 为圆心的圆并且选取半径 恰好为 与 之间的距离. 移动二刻度尺使得它过 点并且 落在 的延长线上并且 落在圆上. 此时, 直尺与 的延长线的夹角就三等分了已知角度.
注记 1.3.9. 著名的 Mohr-Mascheroni 定理说可以只用圆规完成尺规作图 (做出相应的点而不是直线) .
推论 1.3.10 (化圆为方). 不是尺规可作的.
1. | ^ 公元前 429 年, 为了遏制 Delos 岛的瘟疫, 古希腊人根据神谕需要将阿波罗神殿中正立方体的祭坛 (的体积) 加大一倍. |
2. | ^ 传说古希腊的 Anaxagoras 是第一个研究这个问题的人, 似乎与他监狱中观察圆形的太阳和方形的牢窗有关. |