3.6. 习题

3.6.1对称群 ${\mathfrak{S}}_n$ 中的计算

假设 $n⩾2$, 那么, 以下子集均生成 ${\mathfrak{S}}_n$:

1.	假设 $S=\{(i,j)\}$ 是一些对换 ($2$-循环) 的集合并且 $S$ 生成 ${\mathfrak{S}}_n$, 那么, $|S|$ 的最小值是多少?
2.	假设 $|i_0-j_0|$ 与 $n$ 互素. 证明, $S_4=\{(i_0,j_0),(1,2,\cdots ,n)\}$ 生成 ${\mathfrak{S}}_n$.
3.	假设 $n⩾5$. 证明, ${\mathfrak{A}}_n$ 中的所有 $3$-循环是 (在 ${\mathfrak{A}}_n$ 中) 相互共轭的.
4.	证明, ${\mathfrak{A}}_5$ 可以被双对换 $\{(i,j)(k,l)|1⩽i,j,k,l⩽5\text{且两两不同}\}$ 生成.
5.	(${\mathfrak{A}}_5$ 的自同构群) 令 $G={\mathfrak{A}}_5$. a) 假设 $x=(12)(34)\in G$, $y\in G$ 的是一个 $3$ 阶元. 证明, $xy$ 的阶为 $5$ 当且仅当 $y$ 的两个不动点一个在 $\{1,2\}$ 中并且另一个在 $\{3,4\}$ 中. b) 令 $X=\{(u,v)\in G\times G|u,v,uv\text{的阶分别为}2,3,5\}$, 证明, $|X|=120$. c) $\mathbf{Aut}(G)$ 作用在 $X$ 上, 证明, 这个作用是自由的. 据此, $|\mathbf{Aut}(G)|⩽120$. 由于 $\mathbf{Aut}(G)$ 包含 ${\mathfrak{S}}_5$, 从而 $\mathbf{Aut}(G)={\mathfrak{S}}_5$.
6.	(${\mathfrak{A}}_4$ 的自同构群) 用 $(2,3,3)$ (元素的阶) 替换 $(2,3,5)$, 试用类似的方法证明 $\mathbf{Aut}({\mathfrak{A}}_4)={\mathfrak{S}}_4$.
7.	(${\mathfrak{S}}_4$ 的自同构群) 用 $(2,3,4)$ (元素的阶) 替换 $(2,3,5)$, 试用类似的方法证明 $\mathbf{Aut}({\mathfrak{S}}_4)={\mathfrak{S}}_4$.
8.	试用上面关于 ${\mathfrak{A}}_4$ 的自同构群的结论直接证明上一结果.

3.6.2交错群 ${\mathfrak{A}}_n$ ($n⩾5$) 是单群

如果群 $G$ 除了 $1$ 和本身之外没有其它的正规子群, 我们就称 $G$ 是单群. 很明显, 循环群只有在其阶为素数时为单群.

1.	给出 ${\mathfrak{A}}_3$ 和 ${\mathfrak{A}}_4$ 的正规子群.
2.	我们按照以下步骤证明 ${\mathfrak{A}}_5$ 是单群: ∘ 假设 $N⊲{\mathfrak{A}}_5$ 是正规子群并且 $N\ne 1$. 假设 $N$ 包含一个双置换 (两个不交的置换之积) , 不妨设为 $\sigma =(1,2)(3,4)$, 证明, $\tau =(1,5)(3,4)$ 在 ${\mathfrak{A}}_5$ 中与 $\sigma$ 共轭. 特别地, 证明 $\sigma \tau$ 是 $3$-循环. ∘ 假设 $N⊲{\mathfrak{A}}_5$ 是正规子群并且 $N\ne 1$. 假设 $N$ 包含一个 $5$-循环, 不妨设为 $\sigma =(1,2,3,4,5)$, 证明, $\tau =(2,3,1,4,5)$ 在 ${\mathfrak{A}}_5$ 中与 $\sigma$ 共轭. 特别地, 证明 $\tau {\sigma }^2$ 是 $3$-循环. ∘ 假设 $N⊲{\mathfrak{A}}_5$ 是正规子群并且 $N\ne 1$. 证明, $N$ 包含所有的 $3$-循环, 从而, ${\mathfrak{A}}_5$ 是单群.
3.	我们还可以按照以下步骤证明 ${\mathfrak{A}}_5$ 是单群 ∘ 证明, ${\mathfrak{A}}_5$ 有五个共轭类并且每个共轭类中的元素个数分别为 $1,12,12,15$ 和 $20$. ∘ 子群 $N\subset {\mathfrak{A}}_5$ 在 ${\mathfrak{A}}_5$ 的共轭下不变. 证明, $|N|$ 只能等于 $1,13,16,21,25,28,33,36,40,45,48$ 和 $60$. ∘ 证明, ${\mathfrak{A}}_5$ 是单群.
4.	以下假设 $n⩾6$ 并且 ${\mathfrak{A}}_{n-1}$ 是单群. 假设 $N⊲{\mathfrak{A}}_n$ 是正规子群并且 $N\ne 1$, $N\ne {\mathfrak{A}}_n$. ∘ 如果存在 $\sigma \in N-\{1\}$ 使得 $\sigma (n)=n$, 证明, $N={\mathfrak{A}}_n$. ∘ 证明, 对任意的 $\sigma \in N-\{1\}$, 只要 $\{i,j\}\cap \{\sigma (n),n\}=\varnothing$, 那么, $\tau \sigma {\tau }^{-1}\sigma =1$, 其中, $\tau =(i,j)(n,\sigma (n))$. ∘ 同上, 证明, ${\sigma }^2=1$ 并且 $\sigma :\{i,j\}\to \{i,j\}$. (提示: 考虑 ${\sigma }^{-1}\tau \sigma {\tau }^{-1}$) ∘ 证明, $\sigma =(n,\sigma (n))$ 从而得到矛盾. 据此, ${\mathfrak{A}}_n$ 是单群.
5.	假设 $n⩾5$, $G⊲{\mathfrak{S}}_n$ 为正规子群, 证明, 如果 $G\ne 1$, $G\ne {\mathfrak{S}}_n$, 那么, $G={\mathfrak{A}}_n$.
6.	证明, $N=\{1,(1,2)(3,4),(1,3)(2,4),(1,4)(2,3)\}$ 是 ${\mathfrak{S}}_4$ 的正规子群并且 $N⊲{\mathfrak{A}}_4$. ${\mathfrak{S}}_4$ 是哪一个群?
7.	假设 $n⩾5$, $H<{\mathfrak{S}}_n$ 为子群, $d=[{\mathfrak{S}}_n:H]$. 证明, 存在群同态 $\phi :{\mathfrak{S}}_n\to {\mathfrak{S}}_d$, 使得 $\mathrm{Ker}(\phi )<H$. 据此证明, 如果 $H\ne {\mathfrak{A}}_n,{\mathfrak{S}}_n$, 那么, $d⩾n$.
8.	证明, 对于 $n⩾2$, 存在单的群同态 ${\mathfrak{S}}_n\to {\mathfrak{A}}_{n+2}$ (从而 ${\mathfrak{S}}_n$ 可被视作是 ${\mathfrak{A}}_{n+2}$ 的子群) 但是不存在单的群同态 ${\mathfrak{S}}_n\to {\mathfrak{A}}_{n+1}$.

3.6.3$\mathbf{PSL}(2;{\mathbb{F}}_2)\simeq {\mathfrak{S}}_3,\mathbf{PSL}(2;{\mathbb{F}}_3)\simeq {\mathfrak{A}}_4$

循环群只有在其阶为素数时为单群.

1.	证明, $\mathbf{GL}(2;{\mathbb{F}}_2)\simeq \mathbf{PGL}(2;{\mathbb{F}}_2)\simeq \mathbf{SL}(2;{\mathbb{F}}_2)\simeq \mathbf{PSL}(2;{\mathbb{F}}_2)$.
2.	$\mathbf{GL}(2;{\mathbb{F}}_2)$ 在 ${\mathbb{P}}^1({\mathbb{F}}_2)$ 的自然的作用给出同态$$\phi :\mathbf{GL}(2;{\mathbb{F}}_2)⟶{\mathfrak{S}}_{{\mathbb{P}}^1({\mathbb{F}}_2)}\simeq {\mathfrak{S}}_3,$$其中, 后一个同构由以下对应给出 $[1:0]\to 1,[1:1]\to 1,[0:1]\to 3$. 证明, $\phi$ 是群同构.
3.	$\mathbf{GL}(2;{\mathbb{F}}_3)$ 在 ${\mathbb{P}}^1({\mathbb{F}}_3)$ 上自然的作用给出同态$$\phi :\mathbf{GL}(2;{\mathbb{F}}_3)⟶{\mathfrak{S}}_{{\mathbb{P}}^1({\mathbb{F}}_3)}\simeq {\mathfrak{S}}_4,$$其中, 后一个同构由以下对应给出 $[1:0]\to 1,[1:1]\to 2,[1:2]\to 3,[0:1]\to 4$. 计算 $\mathrm{Ker}(\phi )$ 并证明 $\phi$ 诱导出同构$$\overline{\phi }:\mathbf{PGL}(2;{\mathbb{F}}_3)\stackrel{\simeq }{⟶}{\mathfrak{S}}_4.$$
4.	证明, 对 $n⩾2$, ${\mathfrak{S}}_n$ 的指标为 $2$ 的子群必为 ${\mathfrak{A}}_n$. 据此, 利用 $\mathbf{PSL}(2;{\mathbb{F}}_3)$ 在 ${\mathbb{P}}^1({\mathbb{F}}_3)$ 的上自然作用证明: $$\mathbf{PSL}(2;{\mathbb{F}}_3)\simeq {\mathfrak{A}}_4.$$
5.	证明,$$\mathbf{SL}(2;{\mathbb{F}}_4)\simeq \mathbf{PSL}(2;{\mathbb{F}}_4)\simeq {\mathfrak{A}}_5.$$(提醒: 对任意的 $x\in {\mathbb{F}}_4$, $2x=0$. 特别地, $1=-1$. )
6.	$n⩾5$, $H<{\mathfrak{S}}_n$ 的是指标为 $n$ 的子群. 证明, $H\simeq {\mathfrak{S}}_{n-1}$. 据此, 利用 $\mathbf{PGL}(2;{\mathbb{F}}_5)$ 在 ${\mathbb{P}}^1({\mathbb{F}}_5)$ 的上自然作用证明: $$\mathbf{PGL}(2;{\mathbb{F}}_5)\simeq {\mathfrak{S}}_5.$$
7.	一个不同构的结论. ∘ 证明, $\mathbf{SL}(3;{\mathbb{F}}_4)$ 中恰有一个共轭类使得其元素的阶为 $2$. 进一步, 这个共轭类中的元素均恰为剪切映射. ∘ 证明, 自然的映射 $\mathbf{SL}(3;{\mathbb{F}}_4)\to \mathbf{PSL}(3;{\mathbb{F}}_4)$ 给出了这两个群中阶为 $2$ 的元素的一一对应. ∘ 证明, ${\mathfrak{A}}_8$ 与 $\mathbf{PSL}(3;{\mathbb{F}}_4)$ 是具有 $20160$ 个元素但是不同构的单群.

3.6.4$60$ 阶的单群

$G$ 是群, 其阶为 $60$, $s_p$ 为其 Sylow $p$-子群的个数, 如果 $s_5\ne 1$, 那么 $G$ 是单群. 我们用反证法证明这个结论. 假设 $H⊲G$ 并且 $H\ne 1,H\ne G$.

1.	证明, $s_2\in \{1,3,5,15\},s_3\in \{1,4,10\},s_5=6$.
2.	假设 $|H|$ 是 $5$ 的倍数, 证明, $|H|=30$; 进一步证明, $H$ 只有一个 Sylow $5$-子群. 据此推出矛盾.
3.	假设 $|H|⩽4$. 证明, $G$ 只有一个 Sylow $5$-子群; 进一步证明存在 $H^{\prime }⊲G$, $H^{\prime }\ne G$ 并且 $|H^{\prime }|$ 是 $5$ 的倍数. 据此推出矛盾.
4.	假设 $|H|=6$ 或者 $|H|=12$. 证明, $H$ 只有一个 Sylow $2$-子群或只有一个 Sylow $3$-子群. 据此推出矛盾. 以下假设 $G$ 是阶为 $60$ 的单群, $s_p$ 为其 Sylow $p$-子群的个数.
5.	$H<G$ 是子群并且 $H\ne G$. 证明, $[G:H]⩾5$. 进一步证明, 如果 $[G:H]=5$, 那么, $G\simeq {\mathfrak{A}}_5$.
6.	证明, $s_2\in \{5,15\},s_3=4,s_5=6$.
7.	假设 $s_2=5$, 证明, $G\simeq {\mathfrak{A}}_5$.
8.	假设 $s_2=15$, 证明, 存在 Sylow $2$-子群 $P$ 和 $Q$, 使得 $|P\cap Q|=2$. 进一步证明 $P\cap Q$ 的正规化子的指标为 $5$, 即 $[G:{\mathrm{N}}_G(P\cap Q)]=5$.
9.	证明, 阶为 $60$ 的单群在同构的意义下只能是 ${\mathfrak{A}}_5$ 并计算 $s_2$ 的值.

3.6.5不存在 $180$ 阶的单群

$G$ 是群, 其阶为 $180$, 那么, $G$ 不是单群. 我们用反证法证明这个结论. 以下 $s_p$ 为 $G$ 的 Sylow $p$-子群的个数,

1.	(常用结论) 证明, $p^2$ 阶的群必然是交换群, 其中, $p$ 是素数.
2.	证明, $s_3=10$.
3.	证明, $s_5=36$.
4.	$P$ 和 $Q$ 是不同的 Sylow $3$-子群, 证明, $P\cap Q=1$. (提示: 假设 $g\in P\cap Q-\{1\}$, 考虑其中心化子 $C_g(G)$)
5.	据上述结论推出矛盾.

3.6.6与 Sylow $p$-子群相关的补充

1.	$G$ 是有限群, $S<G$ 是一个 Sylow $p$-子群. 证明, $[G:{\mathrm{N}}_G(S)]\equiv 1(\mathrm{mod}p)$.
2.	$G$ 是有限群, $S<G$ 是一个 Sylow $p$-子群, $H⊲G$ 是正规子群. 证明, $S\cap H$ 是 $H$ 的 Sylow $p$-子群.
3.	$G$ 是有限群, $H⊲G$ 是正规子群, $\pi :G\to G$ 是自然投影. 证明, 如果 $S<G$ 是 Sylow $p$-子群, 那么, $\pi (S)$ 是 $G$ 的 Sylow $p$-子群; 反之, 如果 $S^{\prime }<G$ 是 Sylow $p$-子群, 那么, 存在 $G$ 的 Sylow $p$-子群 $S$, 使得 $\pi (S)=S^{\prime }$.
4.	(Frattini 技巧) ∘ 群 $G$ 作用在集合 $X$ 上, $H<G$ 是子群, 那么, ${}^{G\curvearrowright }X$ 诱导出 ${}^{H\curvearrowright }X$. 假设 ${}^{H\curvearrowright }X$ 是传递的, 证明, 对任意的 $x\in X$, $G=H\cdot {\mathrm{Stab}}_G(x)$. ∘ (Frattini) $G$ 是群, $H⊲G$ 是有限的正规子群, $S<H$ 是 $H$ 的一个 Sylow $p$-子群. 证明, $G=H\cdot {\mathrm{N}}_G(S)$.
5.	$G$ 是有限群, $S<G$ 是一个 Sylow $p$-子群, $H<G$ 是子群并且 $H\supset N_G(S)$. 证明, $H={\mathrm{N}}_G(H)$.
6.	$G$ 是有限群, $S<G$ 是一个 Sylow $p$-子群. 证明, ${\mathrm{N}}_G(S)={\mathrm{N}}_G({\mathrm{N}}_G(S))$.

3.6.7$\mathbf{PSL}(2;{\mathbb{F}}_7)$ 与 $\mathbf{GL}(3;{\mathbb{F}}_2)$ 同构

我们记 ${\mathbf{P}}^1({\mathbb{F}}_p)$ 为 ${\mathbb{F}}_p\cup \{\infty \}$, 对于 $g=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\in \mathbf{GL}(2;{\mathbb{F}}_p)$, 它通过分式线性变换在 ${\mathbf{P}}^1({\mathbb{F}}_p)$ 上作用: $$g\cdot x=\frac{ax+b}{cx+d}.$$这给出了单的群同态$$\mathbf{PGL}(2;{\mathbb{F}}_p)⟶{\mathfrak{S}}_{{\mathbf{P}}^1({\mathbb{F}}_p)}\simeq {\mathfrak{S}}_{p+1}.$$从而, 我们可以把 $\mathbf{PGL}(2;{\mathbb{F}}_p)$ 视为 ${\mathfrak{S}}_{p+1}$ (因为 $|{\mathbf{P}}^1({\mathbb{F}}_p)|=p+1$) 中阶为 $p^3-p$ 并且在 $\{1,2,\cdots ,p+1\}$ 上传递作用的子群. 考虑群 $\mathbf{PGL}(2;{\mathbb{F}}_p)$ 通过分式线性变换在 ${\mathbf{P}}^1({\mathbb{F}}_p)$ 上的作用, 令 ${\mathbf{Aff}}_1({\mathbb{F}}_p)=\mathrm{Stab}(\infty )$. 容易看出, ${\mathbf{Aff}}_1({\mathbb{F}}_p)$ 在 ${\mathbb{F}}_p={\mathbf{P}}^1({\mathbb{F}}_p)-\{\infty \}$ 上的作用是双传递的并且 $⟨{\mathbf{Aff}}_1({\mathbb{F}}_p),\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)⟩=\mathbf{PGL}(2;{\mathbb{F}}_p)$. Zassenhaus 有一个有意思的结果: 令 $X={\mathbf{P}}^1({\mathbb{F}}_p)$, $G<{\mathfrak{S}}_X$ 的阶为 $p^3-p$ 并且在 $X$ 上传递作用, 那么, 存在 $\sigma \in {\mathfrak{S}}_X$, 使得 $\sigma G{\sigma }^{-1}=\mathbf{PGL}(2;{\mathbb{F}}_p)$. 我们对 $p=3\mathrm{mod}4$ 的情形证明该结论, 证明的想法是逐步在 $G$ 中构造出 ${\mathbf{Aff}}_1({\mathbb{F}}_p)$ 以及 $\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$ 所对应的对象.

我们使用如下的约定与假设: $$G<{\mathfrak{S}}_X,|G|=p^3-p,\mathbf{PGL}(2;{\mathbb{F}}_p)<{\mathfrak{S}}_X,\alpha (x)=x+1\in {\mathbf{Aff}}_1({\mathbb{F}}_p),$$并且 $G$ 在 $X$ 上的作用是传递的.

1.	证明, $G$ 包含 $p$-循环从而存在 $\sigma \in G$, 使得 $\alpha \in \sigma G{\sigma }^{-1}$. 自此, 假设 $\alpha \in G$.
2.	令 $G_{\infty }=\{g\in G|g(\infty )=\infty \}$. 证明, $|G_{\infty }|=p^2-p$, $P=⟨\alpha ⟩⊲G_{\infty }$ 并且对任意 $g\in G_{\infty }$, 存在 $a\in [1,p)$, 使得 $g\cdot \alpha ={\alpha }^a\cdot g$ ($a$ 当然依赖于 $g$) .
3.	证明, $G_{\infty }={\mathbf{Aff}}_1({\mathbb{F}}_p)$.
4.	证明, $G$ 在 $X$ 上的作用是 $3$-传递的并且若 $g\in G$ 固定任 $3$ 个不同的点则 $g=1$. 以下选取 $\gamma \in G$ 使得 $\gamma (0)=\infty ,\gamma (\infty )=0,\gamma (1)=1$ (我们希望它对应着 $\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$) 并令$$\{\begin{array}{ll}& C=\{g\in G|g(\infty )=\infty ,g(0)=0\},\\ & C^{\prime }={\mathrm{C}}_{{\mathfrak{S}}_X}(C)=\{g\in G|gc=cg,\forall c\in C\}.\end{array}$$
5.	证明, $C$ 是阶为 $p-1$ 的循环群并由某个 (${\mathfrak{S}}_X$ 中的) $p-1$ 循环生成; $C^{\prime }=⟨C,(0,\infty )⟩$, 其中, $(0,\infty )$ 是 ${\mathfrak{S}}_X$ 中的对换.
6.	证明, 若 $G$ 中有对换, 则 $G={\mathfrak{S}}_X$, 从而 $p=2$ 或 $3$. 自此, 假设 $p⩾5$ 并且 $(0,\infty )\notin G$.
7.	证明, $C^{\prime }\cap G=C$ 并且$$\mathrm{Int}(\gamma ):G\to G,g\mapsto \gamma g{\gamma }^{-1}$$是阶为 $2$ 的自同构.
8.	证明, 存在 $n\in [2,p-2]$, 使得 $n^2=1\mathrm{mod}p-1$ 并且对任意的 $c\in C$, $\mathrm{Int}(\gamma )(c)=c^n$; 对任意的 $x\in X-\{\infty \}$, $\gamma \cdot x=x^n$, 其中, $x^n$ 是在 $X-\{\infty \}={\mathbb{F}}_p$ 中的运算.
9.	证明, $n\equiv -1\mathrm{mod}\frac{p-1}{2}$. (提示: $\gamma$ 至多有两个不动点)
10.	证明, 如果 $p=3\mathrm{mod}4$, 那么, $n+1=0\mathrm{mod}p-1$ 并且 $G=\mathbf{PGL}(2;{\mathbb{F}}_p)$. 至此, 我们在 $p=3\mathrm{mod}4$ 的假设下证明了 Zassenhaus 的结论.
11.	(应用) $G$ 是群, $p$ 是素数, $|G|=p^3-p$. 我们做如下假设: 如果 $H⊲G$ 并且 $|H|$ 整除 $p^2-p$, 那么 $H=1$. 1. 证明, $G$ 有 $p+1$ 个 Sylow $p$-子群. 2. 证明, $G$ 通过共轭在 Sylow $p$-子群的集合上的作用是忠实的. 3. 证明, 若 $p=3\mathrm{mod}4$, 则 $G\simeq \mathbf{PGL}(2;{\mathbb{F}}_p)$.
12.	($\mathbf{GL}(3;{\mathbb{F}}_2)\simeq \mathbf{PSL}(2;{\mathbb{F}}_7)$) 令 $N=\mathbf{GL}(3;{\mathbb{F}}_2)$, 则 $A\in N$ 为 $3\times 3$ 的矩阵. 定义 $\mathbb{Z}$ 在 $N$ 上的作用为: $$\psi :\mathbb{Z}\to \mathbf{Aut}(N),1\mapsto \left(A\mapsto {}^t{A}^{-1}\right).$$令 $G=N{⋊}_{\psi }\mathbb{Z}$. 1. 证明, 不存在 $M\in \mathbf{GL}(3;{\mathbb{F}}_2)$, 使得对任意的 $A\in \mathbf{GL}(3;{\mathbb{F}}_2)$, ${}^{t}AMA=M$ 并进一步证明 $G$ 的正规子群的指标不等于 $2$. 2. 证明, $G$ 只有一个非平凡正规子群 $N\times \{0\}=\{(A,0)\in N{⋊}_{\psi }\mathbb{Z}|A\in N\}\simeq N$. 3. 证明, $G\simeq \mathbf{PGL}(2;{\mathbb{F}}_7),N\simeq \mathbf{PGL}(2;{\mathbb{F}}_7)$. 这就证明了 $\mathbf{GL}(3;{\mathbb{F}}_2)\simeq \mathbf{PSL}(2;{\mathbb{F}}_7)$.

3.6.8最少的生成元个数

$G$ 是群, 如果存在有限个 $x_1,\cdots ,x_n$, 使得 $G=⟨x_1,\cdots ,x_n⟩$, 我们就称 $G$ 是有限生成的. 以上最小可能的 $n$ 被称作是 $G$ 的最少的生成元个数, 记作 $\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}(G)$. 我们规定 $\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}(\{1\})=0$.

1.	证明, $\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}(G)=1$ 等价于 $G$ 是非平凡的循环群.
2.	假设 $n⩾3$. 证明, $\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}({\mathfrak{S}}_n)=2$.
3.	$p$ 是素数, $r$ 是自然数, $G={\left(\mathbb{Z}\right)}^r=\underset{r\text{个}}{\underbrace{\mathbb{Z}\times \cdots \times \mathbb{Z}}}$. 证明, $\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}(G)=r$. (提示: 将 $G$ 视为 $\mathbb{Z}$-线性空间)
4.	$G$ 是有限生成群, 假设有满的群同态 $\phi :G⟶G^{\prime }$. 证明, $G^{\prime }$ 是有限生成群并且$$\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}(G^{\prime })⩽\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}(G).$$
5.	$G$ 是群, $H⊲G$ 是正规子群. 证明, 如果 $H$ 和 $G$ 是有限生成的, 那么, $G$ 也是并且$$\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}(G)⩽\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}\left(G\right)+\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}(H).$$
6.	对于群 $A=\prod _{i=1}^s\mathbb{Z}$, 其中, $s\in {\mathbb{Z}}_{⩾1},d_1,\cdots ,d_s\in {\mathbb{Z}}_{⩾2}$, 使得 $d_s\mid d_{s-1},d_{s-1}\mid d_{s-2},\cdots ,d_2\mid d_1$. 证明, $\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}(A)=s$.
7.	对于群 $A={\mathbb{Z}}^r=\underset{r\text{个}}{\underbrace{\mathbb{Z}\times \cdots \times \mathbb{Z}}}$. 证明, $\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}(A)=r$. 据此证明, 如果 ${\mathbb{Z}}^r\simeq {\mathbb{Z}}^{r^{\prime }}$, 那么, $r=r^{\prime }$.
8.	(子群生成元个数可以更多) 对任意的 $n⩾3$, 给出如下的例子: $G$ 是群, $H<G$ 是子群, $\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}(G)=2$ 而 $\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}(H)=n$.
9.	(有限生成群的子群未必有限生成) 令 $G=⟨\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right),\left(\begin{array}{cc}2& 0\\ 0& 1\end{array}\right)⟩<\mathbf{GL}(2;\mathbb{Q})$ 是由两个元素生成的群. 证明, $H=\left\{\left(\begin{array}{cc}1& \frac{m}{2^k}\\ 0& 1\end{array}\right)|k\in {\mathbb{Z}}_{⩾0},m\in \mathbb{Z}\right\}$ 是 $G$ 的子群并且不是有限生成的.
10.	(有限生成交换群子群的生成元个数) $G$ 是有限生成交换群, $H<G$ 是子群. 证明, $$\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}(H)⩽\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}(G).$$(提示: 找一个 $g\in G$, 使得 $\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}\left(G\right)<\mathrm{mi}{\mathrm{n}}_{\mathrm{gen}}(G)$)
11.	$r⩾1$, $A$ 是 ${\mathbb{Z}}^r$ 的子群. 证明, 存在 $r^{\prime }⩽r$, 使得 $A\simeq {\mathbb{Z}}^{r^{\prime }}$.

3.6.9阶为 $p^3$ 的群有 $5$ 个, $p\ne 2$

假设 $p$ 是奇素数. 用 ${\mathbb{F}}_p$ 表示 $p$ 个元素的有限域, 用 $\mathbb{Z}$ 表示其加法群.

1.	在同构意义下, 写下所有阶为 $2^3$ 的群和阶为 $p^2$ 的群.
2.	我们在课上用对角线均为 $1$ 的上三角矩阵给出了 $\mathbf{GL}(2;{\mathbb{F}}_p)$ 一个 Sylow 子群. 计算 $\mathbf{GL}(2;{\mathbb{F}}_p)$ 中 Sylow $p$-子群的个数.
3.	给定两个非平凡的群同态 $\phi :\mathbb{Z}⟶\mathbf{GL}(2;{\mathbb{F}}_p)$ 和 ${\phi }^{\prime }:\mathbb{Z}⟶\mathbf{GL}(2;{\mathbb{F}}_p)$. 对任意的整数 $k$, 令 ${\phi }_k(x)=\phi (kx)$, 其中, $x\in \mathbb{Z}$. 证明, 存在 $A\in \mathbf{GL}(2;{\mathbb{F}}_p)$ 和 $k=1,2,\cdots ,p-1$, 使得对任意的 $x\in \mathbb{Z}$, 有$${\phi }^{\prime }(x)=A\cdot {\phi }_k(x)\cdot A^{-1}.$$
4.	在同构的意义下, 可能的半直积 $\left(\mathbb{Z}\times \mathbb{Z}\right){⋊}_{\psi }\mathbb{Z}$ 恰有两个. 进一步证明, 其中恰有一个是非交换群并且其中心同构于 $\mathbb{Z}$.
5.	$G$ 是群, $|G|=p^3$. 假设 $G$ 不是循环群并且存在 $g\in G$ 使得 $\mathrm{ord}(g)=p^2$. 证明, $⟨g⟩⊲G$.
6.	证明, 在同构的意义下, 上一个小问题中的群恰好两个.
7.	在同构意义下, 写下所有阶为 $p^3$ 的群.

3.6.10射影几何、Fano 平面与 $\mathbf{GL}(3;\mathbb{F}2)$

给定非空集合 $\Pi$ 和 $\Lambda$, 我们把 $\Pi$ 中的元素 $p$ 称作点, $\Lambda$ 中的元素 $l$ 称作线. 集合 $\Pi$ 和 $\Lambda$ 之间重合关系 (incidence relation) 指的是乘积集合的子集 $I\subset \Pi \times \Lambda$. 对任意的 $(p,l)\in \Pi \times \Lambda$, 若 $(p,l)\in I$, 我们就说点 $\mathbf{p}$ 在线 $\mathbf{l}$ 上或线 $\mathbf{l}$ 过点 $\mathbf{p}$. 进一步, 如果以下三条公理成立:

公理 1	两点确定一条线, 即对任两个不同的点 $p,p^{\prime }\in \Pi$, 存在唯一的线 $l\in \Lambda$, 使得 $l$ 过 $p$ 且过 $p^{\prime }$;
公理 2	两线交于一个点, 即对任两条不同的线 $l,l^{\prime }\in \Pi$, 存在唯一的点 $p\in \Lambda$, 使得 $l$ 和 $l^{\prime }$ 均过 $p$;
公理 3	存在四个不同的点 $p_1,p_2,p_3,p_4\in \Pi$, 任意的 $l\in \Lambda$ 不能同时过其中的三点.

我们就称 $(\Pi ,\Lambda ;I)$ 或 $\Pi$ 为射影平面. 在公理 2 的条件下, 我们还称 $p$ 是 $l$ 与 $l^{\prime }$ 的交点.

$(\Pi ,\Lambda ;I)$ 和 $({\Pi }^{\prime },{\Lambda }^{\prime };I^{\prime })$ 为射影平面, 如果存在双射$$\phi :\Pi \to {\Pi }^{\prime },\psi :\Lambda \to {\Lambda }^{\prime },$$使得 $(p,l)\in I$ 当且仅当 $(\phi (p),\psi (l))\in I^{\prime }$, 就称 $(\phi ,\psi )$ 是 $(\Pi ,\Lambda ;I)$ 与 $({\Pi }^{\prime },{\Lambda }^{\prime };I^{\prime })$ 之间的同构. 令 $\mathbf{Aut}(\Pi ,\Lambda ;I)$ 为 $(\Pi ,\Lambda ;I)$ 到自身同构的集合, 它在映射的复合下是群.

1.	第一部分, 射影平面与 Fano 平面 $K$ 是域, $V$ 是 $3$ 维 $K$-线性空间, $V^{\ast }$ 为其对偶. 令 $\Pi =\mathbf{P}(V),\Lambda =\mathbf{P}(V^{\ast })$. 我们要把 $\mathbf{P}(V)$ 中的线定义为 $V$ 中的 $2$ 维线性子空间: 对任意的 $p\in \Pi$, 不妨选取 $p\in V$ 作为其代表; 对任意的 $l\in \Lambda$, 不妨选取 $l\in V^{\ast }$ 作为其代表, 我们定义$$I=\{(p,l)|l(p)=0\}.$$证明, 以上是良好定义的并且 $(\Pi ,\Lambda ;I)$ 为射影平面.
2.	$(\Pi ,\Lambda ;I)$ 为射影平面. 证明, 存在四条不同的线 $l_1,l_2,l_3,l_4\in \Lambda$, 任意的 $p\in \Pi$ 不能同时在其中的三条线上. 据此构造重合关系 $I^{\ast }\subset \Lambda \times \Pi$, 使得 $(\Lambda ,\Pi ;I^{\ast })$ 为射影平面.
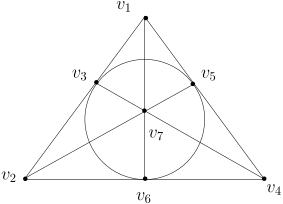
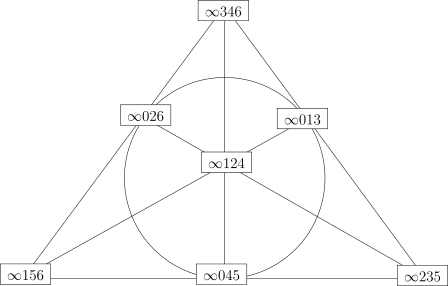
3.	(元素个数最小的射影平面的构造) 令 $\Pi ={\mathbf{P}}^2({\mathbb{F}}_2)$, 则 $|\Pi |=7$ 每个点均对应 $({\mathbb{F}}_2{)}^3$ 中非零向量$$v_1=(0,0,1),v_2=(0,1,0),v_3=(0,1,1),v_4=(1,0,0),v_5=(1,0,1),v_6=(1,1,0),v_7=(1,1,1).$$ 上图中有 $6$ 条直线段和一个圆, 每个这样的图形上有三个点, 它们对应着 $\Lambda$. 这个射影平面被称作是 Fano 平面. 1. $(\Pi ,\Lambda ;I)$ 为射影平面, $p_1,p_2,p_3,p_4\in \Pi$ 满足公理 3. 令 $l_{ij}$ 为过 $p_i$ 与 $p_j$ 的直线, 其中, $1⩽i,j⩽4$; 令 $p_5,p_6,p_7$ 分别为 $l_{12}$ 与 $l_{34}$、$l_{13}$ 与 $l_{24}$ 以及 $l_{14}$ 与 $l_{23}$ 的交点. 证明, $\{p_1,\cdots ,p_7\}$ 这 $7$ 个点两两不同. 2. $(\Pi ,\Lambda ;I)$ 为射影平面并且 $|\Pi |=7$. 假设 $p_1,p_2,p_3,p_4\in \Pi$ 满足公理 3, 以上已经构造了 $6$ 条线 $l_{ij}$ 并且 $\{p_1,\cdots ,p_7\}=\Lambda$. 令 $l_{\infty }$ 为过 $p_5,p_6$ 的线, 证明, $l_{\infty }$ 过 $p_7$. 进一步证明, $\Lambda =\{l_{ij},l_{\infty },1⩽i,j⩽4\}$ 恰有 $7$ 条线并且每条线恰好过 $3$ 个点. 3. 证明, 以下映射$$\{\begin{array}{ll}& p_1\mapsto (1,1,1),p_2\mapsto (1,0,1),p_3\mapsto (1,1,0),\\ & p_4\mapsto (1,0,0),p_5\mapsto (0,1,0),p_6\mapsto (0,0,1),p_7\mapsto (0,0,1).\end{array}$$可以给出 $(\Pi ,\Lambda ;I)$ 到 Fano 平面的同构. 以上证明了 Fano 平面是元素个数最小的唯一的 (在同构意义下) 射影平面.
4.	第二部分, 群 $\mathbf{GL}(3;{\mathbb{F}}_2)$ 中 Fano 平面的结构 $\mathbf{GL}(3;{\mathbb{F}}_2)$ 在 Fano 平面的点集 $\Pi$ 上有自然作用; $\mathbf{GL}(3;{\mathbb{F}}_2)$ 在 Fano 平面的线集 $\Lambda$ 上也有自然作用 (把直线映射称直线) . 所以, $\mathbf{GL}(3;{\mathbb{F}}_2)$ 可以自然地作用在 $\Pi \times \Lambda$ 上. 这个作用有几个轨道?
5.	在 $\mathbf{GL}(3;{\mathbb{F}}_2)$ 中的标准 Borel 子群 $B$ 是对角线线上均为 $1$ 的上三角矩阵的集合, 包含 $B$ 的子群被称作是标准抛物子群, 比如下述的 $P,Q<\mathbf{GL}(3;{\mathbb{F}}_2)$: $$B=\left\{\left(\begin{array}{ccc}1& \ast & \ast \\ 0& 1& \ast \\ 0& 0& 1\end{array}\right)\right\},P=\left\{\left(\begin{array}{ccc}\ast & \ast & \ast \\ \ast & \ast & \ast \\ 0& 0& 1\end{array}\right)\right\},Q=\left\{\left(\begin{array}{ccc}1& \ast & \ast \\ 0& \ast & \ast \\ 0& \ast & \ast \end{array}\right)\right\}.$$我们注意到 $P\cap Q=B$, $Q=\mathrm{Stab}((1,0,0))$, 其中, $p=(1,0,0)\in \Pi$. 试找出直线 $l\in \Lambda$, 使得 $P=\mathrm{Stab}(l)$. 证明, 与 $P$ 和 $Q$ 共轭的矩阵恰好都是 $7$ 个并且 $P$ 与 $Q$ 不共轭.
6.	假设 $P^{\prime }<\mathbf{GL}(3;{\mathbb{F}}_2)$ 与 $P$ 共轭, $Q^{\prime }<\mathbf{GL}(3;{\mathbb{F}}_2)$ 与 $Q$ 共轭. 证明, 存在 $(p^{\prime },l^{\prime })\in \Pi \times \Lambda$, 使得 $P^{\prime }$ 和 $Q^{\prime }$ 分别为 $l^{\prime }$ 与 $p^{\prime }$ 的稳定化子并且$$|P^{\prime }\cap Q^{\prime }|=\{\begin{array}{l}8,\text{若 p′ 在 l′ 上};\\ 6,\text{若 p′ 不在 l′ 上}.\end{array}$$
7.	按如下方式定义 $P$ 和 $Q$ 的子群: $$M=\left\{\left(\begin{array}{ccc}\ast & \ast & 0\\ \ast & \ast & 0\\ 0& 0& 1\end{array}\right)\right\},U=\left\{\left(\begin{array}{ccc}1& 0& \ast \\ 0& 1& \ast \\ 0& 0& 1\end{array}\right)\right\},N=\left\{\left(\begin{array}{ccc}1& 0& 0\\ 0& \ast & \ast \\ 0& \ast & \ast \end{array}\right)\right\},V=\left\{\left(\begin{array}{ccc}1& \ast & \ast \\ 0& 1& 0\\ 0& 0& 1\end{array}\right)\right\}.$$证明, $U⊲P$ 并且 $P=U⋊M$; $V⊲Q$ 并且 $Q=V⋊N$.
8.	证明, $U$ 和 $V$ 在 $\mathbf{GL}(3;{\mathbb{F}}_2)$ 中不共轭; 每个 $\mathbf{GL}(3;{\mathbb{F}}_2)$ 中同构于 $\mathbb{Z}\times \mathbb{Z}$ 的子群都共轭于 $U$ 或者 $V$; $U$ 和 $V$ 在 $\mathbf{GL}(3;{\mathbb{F}}_2)$ 中各有 $7$ 个与之共轭的子群, 它们被记作$${\Pi }^{\prime }=\{U_1,U_2,\cdots ,U_7\},{\Lambda }^{\prime }=\{V_1,V_2,\cdots ,V_7\}.$$
9.	证明, 对任意 $U^{\prime }\in {\Pi }^{\prime },V^{\prime }\in {\Lambda }^{\prime }$, 若 $U^{\prime }\cap V^{\prime }\ne \varnothing$, 则 $U^{\prime }\cap V^{\prime }=\{1,z\}$, 其中, $z\in \mathbf{GL}(3;{\mathbb{F}}_2)$ 是一个 $2$ 阶元. 进一步, $z$ 的中心化子 $\mathrm{C}(z):={\mathrm{C}}_{\mathbf{GL}(3;{\mathbb{F}}_2)}(z)$ 是 $\mathbf{GL}(3;{\mathbb{F}}_2)$ 的包含 $U^{\prime }$ 和 $V^{\prime }$ 的 Sylow $2$-子群.
10.	证明, $\mathbf{GL}(3;{\mathbb{F}}_2)$ 中恰有 $21$ 个 $2$ 阶元并且它们两两共轭. 进一步证明以下映射是双射: $$\left\{\text{GL(3;F2) 中的 2 阶元}\right\}⟶\left\{\text{GL(3;F2) 的 Sylow 2-子群}\right\},z\mapsto \mathrm{C}(z).$$
11.	定义 ${\Pi }^{\prime }$ 和 ${\Lambda }^{\prime }$ 上的重合关系: $$I^{\prime }=\{(U^{\prime },V^{\prime })\in {\Pi }^{\prime }\times {\Lambda }^{\prime }|U^{\prime }\cap V^{\prime }\ne \varnothing \}$$证明, $({\Pi }^{\prime },{\Lambda }^{\prime },I^{\prime })$ 是 Fano 平面.
12.	第三部分, 应用: $\mathbf{PSL}(2;{\mathbb{F}}_7)\simeq \mathbf{GL}(3;{\mathbb{F}}_2)$ 证明, $\mathbf{PSL}(2;{\mathbb{F}}_7)$ 中的 $2$ 阶元有 $21$ 个并且以下为其 (矩阵表示的) 清单: $$\begin{array}{rl}& z_1=\left(\begin{array}{cc}4& 3\\ 6& 3\end{array}\right),z_2=\left(\begin{array}{cc}1& 1\\ 5& 6\end{array}\right),z_3=\left(\begin{array}{cc}1& 6\\ 2& 6\end{array}\right),z_4=\left(\begin{array}{cc}1& 4\\ 3& 6\end{array}\right),z_5=\left(\begin{array}{cc}1& 5\\ 1& 6\end{array}\right),z_6=\left(\begin{array}{cc}4& 2\\ 2& 3\end{array}\right),\\ & z_7=\left(\begin{array}{cc}1& 3\\ 4& 6\end{array}\right),z_8=\left(\begin{array}{cc}0& 2\\ 3& 0\end{array}\right),z_9=\left(\begin{array}{cc}0& 4\\ 5& 0\end{array}\right),z_{10}=\left(\begin{array}{cc}2& 1\\ 2& 5\end{array}\right),z_{11}=\left(\begin{array}{cc}4& 4\\ 1& 3\end{array}\right),z_{12}=\left(\begin{array}{cc}4& 5\\ 5& 3\end{array}\right),\\ & z_{13}=\left(\begin{array}{cc}2& 2\\ 1& 5\end{array}\right),z_{14}=\left(\begin{array}{cc}4& 6\\ 3& 3\end{array}\right),z_{15}=\left(\begin{array}{cc}2& 4\\ 4& 5\end{array}\right),z_{16}=\left(\begin{array}{cc}1& 2\\ 6& 6\end{array}\right),z_{17}=\left(\begin{array}{cc}2& 5\\ 6& 5\end{array}\right),z_{18}=\left(\begin{array}{cc}0& 1\\ 6& 0\end{array}\right),\\ & z_{19}=\left(\begin{array}{cc}2& 6\\ 5& 5\end{array}\right),z_{20}=\left(\begin{array}{cc}4& 1\\ 4& 3\end{array}\right),z_{21}=\left(\begin{array}{cc}2& 3\\ 3& 5\end{array}\right).\end{array}$$
13.	证明, $\mathbf{GL}(3;{\mathbb{F}}_2)$ 中同构于 $\mathbb{Z}\times \mathbb{Z}$ 的子群共有 $14$ 个, 每个群以及群中的元素由如下清单给出: $${\Pi }^{\prime \prime }=\left\{\begin{array}{rl}& \{1,z_1,z_8,z_{10}\},\{1,z_2,z_7,z_{17}\}\\ & \{1,z_3,z_{16},z_{21}\},\{1,z_4,z_5,z_{19}\},\\ & \{1,z_6,z_{11},z_{20}\},\{1,z_9,z_{13},z_{14}\},\\ & \{1,z_{12},z_{15},z_{18}\}\end{array}\right\},{\Lambda }^{\prime \prime }=\left\{\begin{array}{rl}& \{1,z_1,z_{12},z_{14}\},\{1,z_2,z_5,z_{15}\}\\ & \{1,z_3,z_4,z_{13}\},\{1,z_6,z_8,z_{21}\},\\ & \{1,z_7,z_{10},z_{16}\},\{1,z_8,z_{11},z_{19}\},\\ & \{1,z_9,z_{17},z_{20}\}\end{array}\right\},$$并且以上 ${\Pi }^{\prime \prime }$ 与 ${\Lambda }^{\prime \prime }$ 恰好是这些群的共轭类.
14.	定义 ${\Pi }^{\prime \prime }$ 和 ${\Lambda }^{\prime \prime }$ 上的重合关系: $$I^{\prime \prime }=\{(p,l)\in {\Pi }^{\prime \prime }\times {\Lambda }^{\prime \prime }|p\cap l\ne \varnothing \}.$$证明, $({\Pi }^{\prime \prime },{\Lambda }^{\prime \prime },I^{\prime \prime })$ 是 Fano 平面.
15.	证明, $\mathbf{PSL}(2;{\mathbb{F}}_7)\simeq \mathbf{GL}(3;{\mathbb{F}}_2)$.
16.	第四部分, 利用交比构造 Fano 平面来证明 $\mathbf{PSL}(2;{\mathbb{F}}_7)\simeq \mathbf{GL}(3;{\mathbb{F}}_2)$ 对任意四个不同的 $z_1,z_2,z_3,z_4\in {\mathbf{P}}^1({\mathbb{F}}_p)={\mathbb{F}}_p\cup \{\infty \}$, 定义其交比为$$[z_1,z_2;z_3,z_4]=\begin{array}{c}\frac{z_1-z_3}{z_1-z_4}\\ \frac{z_2-z_3}{z_2-z_4}\end{array}=\frac{z_1-z_3}{z_1-z_4}\cdot \frac{z_2-z_4}{z_2-z_3}.$$证明, $[z_1,z_2;z_3,z_4]$ 在 $\mathbf{PGL}(2;{\mathbb{F}}_p)$ 的作用下不变, 即对任意 $g\in \mathbf{PGL}(2;{\mathbb{F}}_p)$, $$[g(z_1),g(z_2);g(z_3),g(z_4)]=[z_1,z_2;z_3,z_4].$$(提示: 先证明 $\mathbf{PGL}(2;{\mathbb{F}}_p)$ 可由形如 $\left(\begin{array}{cc}1& \ast \\ 0& 1\end{array}\right),\left(\begin{array}{cc}\ast & 0\\ 0& \ast \end{array}\right)$ 和 $\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$ 的矩阵生成)
17.	给定四个不同的 $z_1,z_2,z_3,z_4\in {\mathbb{F}}_p\cup \{\infty \}$, 令 $\lambda =[z_1,z_2;z_3,z_4]$. 考虑对称群 ${\mathfrak{S}}_4$ 在集合 $\{z_1,z_2,z_3,z_4\}$ 上的作用: 对任意 $\sigma \in {\mathfrak{S}}_4$, $\sigma (z_i)=z_{\sigma (i)}$, 其中, $i=1,2,3,4$. 证明, $\{\sigma (\lambda )=[z_{\sigma (1)},z_{\sigma (2)};z_{\sigma (3)},z_{\sigma (4)}]|\sigma \in {\mathfrak{S}}_4\}$ 所有可能的取值为 $\lambda ,\frac{1}{\lambda },1-\lambda ,\frac{1}{1-\lambda },\frac{\lambda }{1-\lambda },\frac{1-\lambda }{\lambda }$. 令$$H=\{1,(1,2)(3,4),(1,3)(2,4),(1,4)(2,3)\}<{\mathfrak{S}}_4,$$证明, 对任意的 $\sigma \in H$, $\sigma (\lambda )=\lambda$.
18.	证明, 恰好有 $28$ 个四元子集 $\{z_1,z_2,z_3,z_4\}\subset {\mathbb{F}}_7\cup \{\infty \}$, 使得 $[z_1:z_2:z_3:z_4]=3$. 特别地, 通过计算证明含有 $\infty$ 的子集有 $14$ 个, 它们由如下两个集合给出: $${\Pi }_{\ast }=\left\{\begin{array}{rl}& \{\infty ,0,1,3\},\{\infty ,0,2,6\},\\ & \{\infty ,0,4,5\},\{\infty ,1,2,4\}\\ & \{\infty ,1,5,6\},\{\infty ,2,3,5\}\\ & \{\infty ,3,4,6\}\end{array}\right\},{\Lambda }_{\ast }=\left\{\begin{array}{rl}& \{\infty ,0,2,3\},\{\infty ,0,1,5\},\\ & \{\infty ,0,4,6\},\{\infty ,1,3,4\}\\ & \{\infty ,1,2,6\},\{\infty ,2,4,5\}\\ & \{\infty ,3,5,6\}\end{array}\right\}$$
19.	我们定义 ${\Pi }_{\ast }$ 与 ${\Lambda }_{\ast }$ 之间的重合关系为$$I_{\ast }=\{(p,l)\in {\Pi }_{\ast }\times {\Lambda }_{\ast }||p\cap l|=3\}.$$ 证明, $({\Pi }_{\ast },{\Lambda }_{\ast },I_{\ast })$ 是 Fano 平面.
20.	证明, $\{p,\overline{p},l,\overline{l}|p\in {\Pi }_{\ast },l\in {\Lambda }_{\ast }\}$, $\mathbf{PSL}(2;{\mathbb{F}}_7)\simeq \mathbf{GL}(3;{\mathbb{F}}_2)$ 恰好给出了所有交比为 $3$ 的 $28$ 个集合, 其中, $\overline{p}$ 和 $\overline{l}$ 分别为 $p$ 和 $l$ 在 ${\mathbf{P}}^1({\mathbb{F}}_7)$ 中的补集. 从而, $\mathbf{PSL}(2;{\mathbb{F}}_7)$ 可以作用在 $\{\{p,\overline{p}\},\{l,\overline{l}\}|p\in {\Pi }_{\ast },l\in {\Lambda }_{\ast }\}$ 上给出同构 $\mathbf{PSL}(2;{\mathbb{F}}_7)\simeq \mathbf{GL}(3;{\mathbb{F}}_2)$.

3.6.11练习题

1.	证明, 除了阶为 $1$ 和 $2$ 的群外, 每个群都有非平凡的自同构.
2.	(交换性的一个有用判据) $G$ 是群. 证明, $G$ 是交换群等价于 $G$ 是循环群.
3.	(对称群指标的另一种定义) 定义映射$${\epsilon }^{\prime }:{\mathfrak{S}}_n\to \{\pm \},\sigma \mapsto {\epsilon }^{\prime }(\sigma )=\prod _{1⩽i<j⩽n}\frac{\sigma (i)-\sigma (j)}{i-j}.$$证明, ${\epsilon }^{\prime }$ 是群同态并且与之前定义的指标映射 $\epsilon$ 一致.
4.	$G$ 是有限群, $h$ 为其共轭类的个数. 令 $C=\{(x,y)\in G\times G|xy=yx\}$, 证明, $|C|=h|G|$.
5.	有限群 $G$ 作用在有限集 $X$ 上. 证明, 如果 ${}^{G\curvearrowright }X$ 是忠实的, 那么, $|G|$ 整除 $|X|!$; 如果 ${}^{G\curvearrowright }X$ 是自由的, 那么, $|G|$ 整除 $|X|$.
6.	(C.Jordan 的定理) 有限群 $G$ 作用在有限集 $X$ 上. 证明, 如果 ${}^{G\curvearrowright }X$ 是传递的, 那么存在 $g\in G$, 使得对任意的 $x\in X$, $g\cdot x\ne x$.
7.	(Ore 的定理) $G$ 是有限群, $p$ 是 $|G|$ 的最小素因子, $H<G$ 是子群. 如果其指标 $[G:H]=p$, 证明, $H$ 是正规子群.
8.	不用单群的概念来证明 ∘ 存在唯一非平凡的群同态 ${\mathfrak{S}}_n\to \mathbb{Z}$. ∘ 不存在非平凡的群同态 ${\mathfrak{A}}_n\to \mathbb{Z}$. ∘ ${\mathfrak{A}}_n$ 是 ${\mathfrak{S}}_n$ 中唯一的指标为 $2$ 的子群. ∘ ${\mathfrak{A}}_4$ 没有 $6$ 阶子群.
9.	$p$ 是素数, $H<{\mathfrak{S}}_p$ 是 $p$-阶子群. ∘ 证明, 恰有一个 $\sigma \in H$, 使得 $\sigma (1)=2$. ∘ 证明, ${\mathfrak{S}}_p$ 有 $(p-2)!$ 个 Sylow $p$-子群.
10.	$p$ 是奇素数, $p⩽n<p^2$. 证明, ${\mathfrak{S}}_n$ 的 Sylow $p$-子群是交换群.
11.	$p$ 是奇素数, $n=p^2$. 证明, ${\mathfrak{S}}_n$ 的 Sylow $p$-子群不交换.
12.	$n⩾2$, 子群 $H<{\mathfrak{S}}_n$ 的指标为 $n$. 证明, $H\simeq {\mathfrak{S}}_{n-1}$.
13.	证明, 四元数群 ${\mathbf{Q}}_8$ 不能写成两个非平凡子群的半直积.
14.	$N$ 是群, $K$ 是循环群, $\phi :K\to \mathrm{Aut}(N)$ 和 $\psi :K\to \mathrm{Aut}(N)$ 是群同态. 证明, 如果 $\phi (K)=\psi (K)$, 那么, $N{⋊}_{\phi }K\simeq N{⋊}_{\psi }K$. (提示: 请参考第四周讲义关于 $pq$ 阶群分类的讨论)
15.	$G$ 是 $p$-群, $|G|=p^k$. 证明, 对任意的 $l⩽k$, 存在正规子群 $H⊲G$, 使得 $|H|=p^l$. (提示: 利用 $\mathrm{Z}(G)\ne 1$ 以及 $G\to G$ 进行归纳)
16.	$A$ 是交换群. 证明, $A$ 是有限生成的交换群当且仅当存在整数 $n$ 以及满的群同态 ${\mathbb{Z}}^n\to A$.
17.	$A$ 是交换群. 我们定义 $A$ 中的挠元素为下面集合中的元: $$A^{\mathrm{tor}}=\{x\in A|\text{存在}n\in \mathbb{Z},\text{使得}nx=0\}.$$证明, $A^{\mathrm{tor}}$ 是 $A$ 的子群. 进一步证明如果 $A$ 是有限生成的, 那么, $A^{\mathrm{tor}}$ 是有限群并且 $A\simeq A^{\mathrm{tor}}\times {\mathbb{Z}}^r$, 其中, $r$ 是 $A$ 的秩.
18.	$A$ 和 $B$ 是交换群. 证明, $(A\times B{)}^{\mathrm{tor}}\simeq A^{\mathrm{tor}}\times B^{\mathrm{tor}}$.
19.	$A$ 是有限交换群. 证明, 如果 $A$ 不是循环群, 那么, 存在素数 $p$ 和 $A$ 的子群 $H$, 使得 $H\simeq \mathbb{Z}\times \mathbb{Z}$.
20.	$G$ 是有限群并且对任意的 $g\in G$, 有 $g^2=1$. 证明, 存在非负整数 $n$, 使得 $G\simeq \prod _{\text{n个}}\mathbb{Z}$.
21.	对任意的 $n⩾1$. 证明, 存在 $\mathbb{R}$ 的子群 $G$, 使得 $G\simeq \prod _{\text{n个}}\mathbb{Z}$.
22.	$A,B$ 和 $C$ 是有限生成的交换群. 证明如下两个结论: $$1)A\times A\simeq B\times B\Rightarrow A\simeq B;2)A\times C\simeq B\times C\Rightarrow A\simeq B.$$