我们用 + A x 1 , ⋯ , x n ∈ A A = ⟨ x 1 , ⋯ , x n ⟩ ( A , + ) 有限生成的交换群 . 这些元素 { x i } i ⩽ n A
Z Z ╱ n Z Z Z ╱ n Z
有限个有限生成交换群之积是有限生成的交换群. 特别地, Z r = r 个 Z ⊕ ⋯ ⊕ Z
有限生成的交换群的商群是有限生成的.
实际上, 令 B < A x 1 B , ⋯ , x n B A ╱ B
A A n Z n → A
由于通过满同态 Z n → A A Z n A A x 1 , ⋯ , x n Z n ⟶ A , ( λ 1 , ⋯ , λ n ) ↦ i = 1 ∑ n λ i x i .
给定交换群的正合列, 0 → B ⟶ ι A ⟶ π C → 0. B C A A B A ╱ B A
实际上, 令 { b 1 , ⋯ , b k } { c 1 , ⋯ , c l } B C i ⩽ l a i ∈ π − 1 ( c i ) ⊂ A a 1 , ⋯ , a l , ι ( b 1 ) , ⋯ , ι ( b k ) A a ∈ A λ 1 , ⋯ , λ l ∈ Z π ( x ) = i = 1 ∑ l λ i c i ⇔ π ( x − i = 1 ∑ l λ i a i ) = 0. x − i = 1 ∑ l λ i a i ∈ Ker ( π ) = Im ( ι ) λ 1 ′ , ⋯ , λ l ′ ∈ Z x − i = 1 ∑ l λ i a i = j = 1 ∑ k λ j ′ ι ( b j ) ⇔ x = i = 1 ∑ l λ i a i + j = 1 ∑ k λ j ′ ι ( b j ) .
直接用定义证明这个命题需要对 A n n = 1 A n = k A = ⟨ x 1 , ⋯ , x k , x k + 1 ⟩ A ′ = ⟨ x 1 , ⋯ , x k , x k + 1 ⟩ B < A
由于 B ∩ A ′ ⊂ Ker ( B ↪ A → A ╱ A ′ ) B ╱ B ∩ A ′ A ╱ A ′ A ╱ A ′ B ╱ B ∩ A ′ A ′ ∩ B B
以上证明表明, B A φ : Z m ⟶ Z n , m = n
ψ : Z m ↠ Z n m ⩾ n
我们用所谓 mod p mod p : Z n ⟶ ( Z ╱ p Z ) n , ( k 1 , ⋯ , k n ) ↦ ( k 1 mod p , ⋯ , k n mod p ) . p Z n = Ker ( mod p ) Z n ╱ p Z n ≃ ( Z ╱ p Z ) n mod p ψ : ( Z ╱ p Z ) m → ( Z ╱ p Z ) n F p m ⩾ n
V n R n ⩾ 1 G < V 离散子群 (作为 V g ∈ G O ⊂ V G ∩ O = { g } G < V K ⊂ V G ∩ K
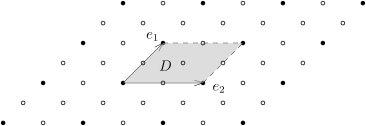
任选 V e = ( e 1 , ⋯ , e n ) e Γ e = i = 1 ⨁ n Z e i = { i = 1 ∑ n k i z i ∣ k i ∈ Z } . V
如果只考虑 e m < n { e 1 , ⋯ , e m } i = 1 ⨁ m Z e i = { i = 1 ∑ m k i z i ∣ k i ∈ Z } . V
上述格点集给出了 V
V n R G < V span R ( G ) = V V e ′ = ( e 1 ′ , ⋯ , e n ′ ) G = Γ e ′
证明. 对维数 n
n = 1 e 1 ∈ G e 1 > 0 G G ∩ [ 0 , e 1 ] G ∩ ( 0 , e 1 ] e 1 ′ = min G ∩ ( 0 , e 1 ] e 1 e 1 ′ l r ∈ [ 0 , e 1 ′ ) e 1 = l ⋅ e 1 ′ + r G r ∈ G e 1 ′ r = 0 e 1 = l ⋅ e 1 ′ ∈ Z g ∈ G e 1 ′ G = Z ⋅ e 1 ′
假设对小于 n e 1 , ⋯ , e n ∈ G V D = { λ 1 e 1 + ⋯ + λ n e n ∣ λ 1 , ⋯ , λ n ∈ [ 0 , 1 )} .
对任意
v ∈ V , 仿照以上的带余除法, 它唯一地表达为
Γ e 与
D 的元素之和:
v = v 1 e 1 + ⋯ + v n e n = v Γ ( ⌊ v 1 ⌋ e 1 + ⋯ + ⌊ v n ⌋ e n ) + v D ( { v 1 } e 1 + ⋯ + { v n } e n ) , 其中,
⌊ x ⌋ 为不超过
x 的最大整数,
{ x } = x − ⌊ x ⌋ . 所以,
G = Γ e + G ∩ D . 根据
G 为离散子群,
G ∩ D ⊂ G ∩ D 是有限集. 定义线性映射
π 1 : V ⟶ R , v 1 e 1 + ⋯ + v n e n ↦ v 1 . 那么,
π 1 为满射并且
Ker ( π 1 ) = V ′ = span ( e 2 , ⋯ , e n ) . 此时,
π 1 ( G ) < R 是子群. 我们断言
π 1 ( G ) 是
R 的离散子群. 根据
G = Γ e + G ∩ D , 我们有
π 1 ( G ) = π ( Γ e ) + π 1 ( G ∩ D ) = ⟨ π 1 ( e 1 )⟩ + π 1 ( G ∩ D ) . 由于
π 1 ( G ∩ D ) 是有限集, 所以
π 1 ( G ) 在
R 中和任何紧集的交有限. 特别地,
π 1 ( G ) 由某个
π 1 ( e 1 ′ ) 生成, 其中,
e 1 ′ ∈ G . 至此, 我们有
G 的子群
⟨ e 1 ′ ⟩ 和
G ∩ V ′ . 很显然,
⟨ e 1 ′ ⟩ ∩ ( G ∩ V ′ ) = 0 并且
⟨ e 1 ′ ⟩ + ( G ∩ V ′ ) = G . 这表明,
G ≃ ( G ∩ V ′ ) × Z e 1 . 对
( G ∩ V ′ ) 用归纳假设即可.
A r ⩾ 0 , d 1 , ⋯ , d s ⩾ 2 d s ∣ d s − 1 , d s − 1 ∣ d s − 2 , ⋯ , d 2 ∣ d 1 A ≃ Z r × i = 1 ∏ s Z ╱ d i Z . r A 秩 , 称 ( d 1 , ⋯ , d s ) A 不变因子 .
{ x 1 , ⋯ , x n } A k 1 , ⋯ , k n ∈ Z 1 y 2 , ⋯ , y n ∈ A { k 1 x 1 + ⋯ + k n x n , y 2 , ⋯ , y n } A
证明. 不妨假设 ∣ k 1 ∣ ⩾ ∣ k 2 ∣ ⩾ ⋯ ⩾ ∣ k n ∣ k 1 > 0
我们对 k = i = 1 ∑ n ∣ k i ∣ { x 1 ′ , ⋯ , x n ′ } k 1 ′ , ⋯ , k n ′ ∈ Z k 1 ′ , ⋯ , k n ′ 1 i = 1 ∑ n ∣ k i ′ ∣ < k k 1 ′ x 1 ′ + ⋯ + k n ′ x n ′ A n
若 k = 1 k 1 x 1 + ⋯ + k n x n = ± x 1 y 2 = x 2 , ⋯ , y n = x n
现在证明
k 的情形. 此时,
k 1 ⩾ ∣ k 2 ∣ , 根据
k 2 的符号
ε , 我们可以做如下的调整:
k 1 x 1 + ⋯ + k n x n = ( k 1 − ε ⋅ k 2 ) x 1 + k 2 ( x 2 + ε ⋅ x 1 ) + k 3 x 3 ⋯ + k n x n . 此时,
x 1 , x 2 + ε x 1 , x 3 , ⋯ , x n 仍然是
A 的总数不超过
n 个的一组生成元. 注意到
k 2 = 0 (否则
k 2 = ⋯ = k n = 0 , 根据
k 1 , ⋯ , k n 的最大公约数为
1 , 就有
k 1 = 1 , 所以这是
k = 1 的情况) , 从而
∣ k 1 − ε ⋅ k 2 ∣ + ∣ k 2 ∣ + ⋯ + ∣ k n ∣ < k . 根据归纳假设, 命题得证.
有限生成的交换群 A 仿基 , 即存在生成元集 { x 1 , ⋯ , x n } ⊂ A i = 1 ∑ n k i x i = 0 ⇔ k i x i = 0 , i = 1 , ⋯ , n .
证明. 选取 A { x 1 , ⋯ , x n } n ord ( x 1 ) ∞ A A 0 = ⟨ x 1 ⟩ A 1 = ⟨ x 2 , ⋯ , x n ⟩ φ : A 0 × A 1 → A , ( a 0 , a 1 ) ↦ a 0 ⋅ a 1 . φ ( ( x 1 , 1 ) ) ↦ x 1 φ ( ( 1 , x i ) ) = x i i ⩾ 2 Im ( φ ) A
现在证明 φ φ ( m 1 x 1 , i = 2 ∑ s m i x i ) = 0 0 ⩽ m 1 < ord ( x 1 ) m 1 x 1 = 0 i = 2 ∑ s m i x i = 0 m 1 ⩾ 1 d = ( m 1 , ⋯ , m n ) d ( k 1 x 1 + k 2 x 2 + ⋯ + k n x n ) = 0 , k i = d m i , ( k 1 , ⋯ , k n ) = 1. y 1 = k 1 x 1 + i = 2 ∑ s k i x i y 2 , ⋯ , y n ord ( y 1 ) ⩽ d ⩽ m 1 < ord ( x 1 ) . ord ( x 1 )
以上推理证明了
⟨ x 1 ⟩ × A 1 ⟶ ≃ A 并且
A 1 的生成元数目不超过
n − 1 . 特别地,
A 1 的生成元数目严格小于
A 0 的最少生成元. 我们再对
A 1 进行以上的分解并将此程继续下去就可以得到一组拟基.
以上证明表明, A A i A Z r × ∏ i = r + 1 n Z ╱ m i Z
A ≃ Z r × ∏ i = r + 1 n Z ╱ m i Z Z ╱ m i Z m i 1 m i = p ∏ p α i ( p ) ⇒ Z ╱ m i Z = p ∏ Z ╱ p α i ( p ) Z . A ≃ Z r × p ∏ i = 1 ∏ s Z ╱ p α i ( p ) Z . d 1 p β ( p ) = max { α i ( p ) } i d 1 = ∏ p β ( p ) β ( p ) { α i ( p ) } i d 2 γ ( p ) = max { α i ( p ) } i d 2 = ∏ p γ ( p ) β ( p ) { α i ( p ) } i d 2 ∣ d 1 , d 3 ∣ d 2 ⋯ A ≃ Z r ( p ∏ Z ╱ p β ( p ) Z ) × ( p ∏ Z ╱ p γ ( p ) Z ) × ⋯ = Z r × i = 1 ∏ s Z ╱ d i Z .
为了证明唯一性, 只要说明
r , d 1 , ⋯ , d s 可以完全由
A 本身计算即可. 先证明关于循环群的一个性质:
A p p k − 1 A ╱ p k A = { 0 , Z ╱ p Z , 若 ∣ A ∣ < ∞ , p k ∤ ∣ A ∣ ; 其余情况。
证明. 设 x A p k − 1 x p k − 1 A p ⋅ p k − 1 x ∈ p k A p k − 1 A ╱ p k A ≃ Z ╱ p Z 或 0. A ≃ Z A A ≃ Z ╱ n Z n = p d ⋅ m ( m , p ) = 1 A ≃ Z ╱ p d Z × Z ╱ m Z = A ′ × Z ╱ m Z A ′ = Z ╱ p d Z ( m , p ) = 1 l Z ╱ m Z → Z ╱ m Z , a ↦ p l a , l = k − 1 , l p k − 1 ⋅ Z ╱ m Z = Z ╱ m Z p k ⋅ Z ╱ m Z = Z ╱ m Z p k − 1 A ╱ p k A ≃ p k − 1 A ′ ╱ p k A ′ . p k − 1 A ′ ╱ p k A ′ A ′ = Z ╱ p d Z
•
如果 d < k p k ∤ ∣ A ∣ k − 1 ⩾ d p k − 1 A ′ = p k − 1 ⋅ Z ╱ p d Z = 0 p k − 1 A ′ ╱ p k A ′ ≃ 0
•
如果 d ⩾ k p k − 1 x ′ = 0 A ′ x ′ A ′ p k − 1 x ′ ∈ / p k A ′ p k − 1 A ′ ╱ p k A ′ ≃ Z ╱ p Z
有限生成交换群结构定理的唯一性部分的证明. 任给存在性部分的一个分解
A ≃ Z r × i = 1 ∏ s Z ╱ d i Z , 我们有
p k − 1 A ╱ p k A ≃ ( Z ╱ p Z ) r × i = 1 ∏ s p k − 1 ( Z ╱ d i Z ) ╱ p k ( Z ╱ d i Z ) . 上述群的阶为
p r + s ( k ) , 其中,
s ( k ) 为
d 1 , ⋯ , d s 中能被
p k 整除的数的个数. 根据
d 1 ∣ d 2 ∣ ⋯ ∣ d s , 这些数恰好是前面的
d 1 , ⋯ , d s ( k ) . 这样, 当
k 取遍
{ 1 , 2 , ⋯ , } 时, 我们可以通过
s ( k ) 的值决定
d 1 , ⋯ , d s 所含
p 因子的幂, 从而决定
d 1 , ⋯ , d s . 通过选取
p 与所有
d 1 , ⋯ , d s 互素, 我们知道
A ╱ p A ≃ ( Z ╱ p Z ) r 决定了
r . 所以, 秩
r 和不变因子
d 1 , ⋯ , d s 完全由群
A 本身决定. 这就给出了唯一性.
我们研究 A = Z ╱ 4 Z × Z ╱ 6 Z A ≃ Z ╱ 4 Z × Z ╱ 6 Z ≃ Z ╱ 2 Z × Z ╱ 2 2 Z × Z ╱ 3 Z . d 1 = 2 2 × 3 d 2 = 2 A ≃ Z ╱ 12 Z × Z ╱ 2 Z .