7. 基本群 (I)

Poincaré 如是说. Ce n’est pas assez, en effet, qu’une science soit légitime : il faut que l’utilité ne puisse en être contestée. Tant d’objets divers sollicitent notre attention, que les plus importants ont seuls droit de l’obtenir.¹

代数拓扑学始于 Henri Poincaré 的 1892 年的长文 “位置分析 (Analys Situs)”. 本节要介绍的基本群 (fundamental group), 或谓 Poincaré 群, 是 Analysis Situs 一文中引入的第二个与拓扑相关的代数结构 (第一个是流形的同调群). 在这一节中我们只介绍最简单的概念和计算. 主要的计算工具将在下一节介绍.

7.1映射的同伦

设 $f$ 和 $g$ 是两个从拓扑空间 $X$ 到拓扑空间 $Y$ 的连续映射. 则一个从 $f$ 到 $g$ 的同伦 (homotopy) 是一个连续映射$$\sigma :X\times [0,1]\to Y,$$它满足, 对任意 $x\in X$, 有 $\sigma (x,0)=f(x)$, $\sigma (x,1)=g(x)$. 若存在从 $f$ 到 $g$ 的同伦, 我们就称 $f$ 与 $g$ 同伦 (homotopic), 有时记作 $f\simeq g$. 同伦于常值映射的连续映射叫做零伦的 (nulhomotopic).

命题 7.1.1. 令 $X,Y$ 为拓扑空间. 则集合 $\mathcal{C}(X;Y)$ 上的关系 “$f$ 同伦于 $g$” 是个等价关系.

证明. 对映射 $f$, 常值同伦 $$\sigma :X\times [0,1]\stackrel{{\mathrm{p}\mathrm{r}}_X}{\to }X\stackrel{f}{\to }Y$$给出了 $f\simeq f$.

如果 $\sigma :X\times [0,1]\to Y$ 是从连续映射 $f$ 到连续映射 $g$ 的同伦, 那么 “相反同伦” $\overline{\sigma }(x,t)=\sigma (x,1-t)$ 是从 $g$ 到 $f$ 的同伦. 从而同伦是对称的关系.

最后证明传递性. 如果 $\sigma :f\simeq g$, $\tau :g\simeq h$, 那么 (利用粘贴引理, 命题 1.5.6) $$(\sigma \ast \tau )(x,t)=\{\begin{array}{ll}\sigma (x,2t)& 0\le t\le 1/2\\ \tau (x,2t-1)& 1/2\le t\le 1\end{array}$$(7.1)是从 $f$ 到 $h$ 的同伦.

$■$

$\mathcal{C}(X;Y)$ 关于同伦关系的商集合记为 $[X;Y]$. 映射 $f$ 的同伦类记作 $[f]$.

例 7.1.2. 设 $P$ 为只有一个点的拓扑空间. 则 $P$ 到拓扑空间 $X$ 的连续映射一一对应于 $X$ 上的点. 而 $P$ 到 $X$ 上两个映射的同伦则相当于连结 $X$ 上两个点的道路. 通过一一对应 $\mathcal{C}(P;X)$ 与 $X$, 同伦关系变成了 $X$ 上 “可以被道路连结” 这个关系. 因此我们得到了一一对应: $[P;X]={\pi }_0(X)$, 其中 ${\pi }_0(X)$ 代表了拓扑空间 $X$ 的道路连通分支构成的集合.

命题 7.1.3. 设 $X,Y$ 和 $Z$ 为拓扑空间. 设从 $X$ 到 $Y$ 的连续映射 $f$, $f^{\prime }$ 同伦, 以及 从 $Y$ 到 $Z$ 的连续映射 $g$, $g^{\prime }$ 同伦. 则复合映射 $g\circ f$ 与 $g^{\prime }\circ f^{\prime }$ 同伦.

证明. 设 $\sigma :X\times [0,1]\to Y$ 为从 $f$ 到 $f^{\prime }$ 的同伦. 设 $\tau :Y\times [0,1]\to Z$ 为从 $g$ 到 $g^{\prime }$ 的同伦. 则 $$\theta (x,t)=\tau (\sigma (x,t),t)$$为从 $g\circ f$ 到 $g^{\prime }\circ f^{\prime }$ 的同伦.

$■$

因此, 映射的复合$$\mathcal{C}(X;Y)\times \mathcal{C}(Y;Z)\to \mathcal{C}(X;Z)$$尊重同伦关系, 因此诱导了自然的映射 (“映射同伦类的复合”)$$(\psi ,\phi )\mapsto \phi \circ \psi :[X;Y]\times [Y;Z]\to [X;Z].$$映射复合的结合律推出了同伦类的复合的结合律.

我们称同伦类 $\phi \in [X;Y]$ 为同伦等价 (homotopy equivalence, Bourbaki 术语 homéotopie), 如果存在 $\psi \in [Y;X]$, 使得 $\phi \circ \psi =[{\mathrm{I}\mathrm{d}}_Y]$, $\psi \circ \phi =[{\mathrm{I}\mathrm{d}}_X]$. 此时称 $\phi$ 与 $\psi$ 互为同伦逆.

7.1.4 (与同伦等价有关的概念与例子).

1.	如果拓扑空间 $X$ 和 $Y$ 通过映射 $f:X\to Y$ 同伦等价, 那么对任何拓扑空间 $T$, 自然映射 $$\begin{array}{rl}[T;X]\to [T;Y],& \chi \mapsto [f]\circ \chi \\ [Y;T]\to [X;T],& \psi \mapsto \psi \circ [f]\end{array}$$都是一一映射. 特别地, 如果 $T$ 是单点拓扑空间, 利用 例 7.1.2, 我们得知 $X$ 的道路连通分支一一对应于 $Y$ 的道路连通分支.
2.	同伦等价于一个点的拓扑空间叫做可缩 (contractible) 的. 实数空间 ${\mathbb{R}}^n$ 中的星形子集都是可缩的. 事实上, 设 $S\subset {\mathbb{R}}^n$ 是星形的, 即存在点 $p\in S$, 使得对任意 $q\in S$, 线段 $\overline{pq}\subset S$. 则我们断言常数映射 $\pi :S\to \{p\}$ 和包含映射 $\iota :\{p\}\to S$ 互为同伦逆. 事实上, $\pi \circ \iota ={\mathrm{I}\mathrm{d}}_{\{p\}}$, 只需证明 $\iota \circ \pi$ 同伦于恒等映射. 这个同伦可以由 $$S\times [0,1]\to S,(q,s)\mapsto sp+(1-s)q$$给出.
3.	令 $X$ 为拓扑空间, $A$ 为 $X$ 的子空间. 则一个从 $X$ 到 $A$ 的形变收缩 (deformation retraction) 是一个同伦 $$r:X\times [0,1]\to X$$使得 $r(x,0)=x$, $r(x,1)\in A$, 并且对任意 $A$ 中的点 $a$, $[0,1]$ 中的点 $t$, 有 $r(a,t)=a$. 如果存在从 $X$ 到子空间 $A$ 的形变收缩, 那么我们就说 $A$ 是 $X$ 的一个形变收缩核 (deformation retract). 如果 $A$ 是 $X$ 的形变收缩核, 那么 $X$ 与 $A$ 同伦等价, 因为形变收缩 $r$ 给出了包含映射 $A\hookrightarrow X$ 的同伦逆. 比如, 映射 $r(x,t)=\frac{x}{(1-t)+t|x|}$ 就给出了 ${\mathbb{R}}^{n+1}\setminus \{0\}$ 到 ${\mathbb{S}}^n$ 的形变收缩. Möbius 带 (例 2.4.2) 的中心圆周是 Möbius 带的形变收缩核.

7.2变体

我们介绍上小节的一些概念的变体.

1.	设 $A$ 是 拓扑空间 $X$ 的子空间. 我们称同伦 $\sigma :X\times [0,1]\to Y$ 是固定 $A$ 的, 如果对任意 $a\in A$, $t\mapsto \sigma (a,t):[0,1]\to Y$ 是常值映射. 如果存在一个固定 $A$ 的从 $f$ 到 $g$ 的同伦, 自然有 $f{|}_A=g{|}_A$, 并且我们称 $f$ 与 $g$ 相对于 $A$ 同伦 (homotopic relative to $A$), 记作 $f{\simeq }_{A}g$.
2.	一个带基点的拓扑空间 (pointed space) 是指一个偶对 $(X,x)$, 其中 $x$ 是拓扑空间 $X$ 上一点. 带基点拓扑空间 $(X,x)$, $(Y,y)$ 之间的一个保持基点的连续映射是指一个满足 $f(x)=y$ 到从 $X$ 到 $Y$ 的连续映射. 保持基点的连续映射构成了函数空间 $\mathcal{C}(X;Y)$ 的子空间 $\mathcal{C}((X,x);(Y,y))$.
3.	两个保持基点的连续映射 $f,g\in \mathcal{C}((X,x);(Y,y))$ 之间的一个保持基点的同伦是指一个固定 $\{x\}$ 的同伦, 即连续映射 $$\sigma :X\times [0,1]\to Y,$$满足, 对任意 $0\le t\le 1$, 有 $\sigma (x,t)=y$. 照搬命题 7.1.1 的证明, 我们知道保持基点的同伦是集合 $\mathcal{C}((X,x);(Y,y))$ 上的一个等价关系, 它的等价类记作 $[(X,x);(Y,y)]$. 类似于命题 7.1.3, 带基点的映射的保持基点的同伦类之间也可以复合,
4.	可以定义带基点的拓扑空间之间 “保持基点同伦等价” 的概念. 这个概念比相对应的拓扑空间彼此同伦等价要强. 带基点的拓扑空间 $(X,x)$ 保持基点地同伦等价于 $(x,x)$, 当且仅当 $x$ 是 $X$ 的形变收缩核. 但习题 7.7.6 提供了一个带基点的空间 $(X,x)$ 的例子, 拓扑空间 $X$ 本身同伦等价于单点空间, 但它上面任何的点都不是形变收缩核.

7.3道路的同伦与基本群

在本节中, 我们采用如下术语.

$\diamond$	拓扑空间 $X$ 上的一条道路是指一个连续映射 $c:[0,1]\to X$.
$\diamond$	道路 $l:[0,1]\to X$ 叫做一个基于点 $x\in X$ 的回路, 如果 $l(0)=l(1)$. 令 $q:[0,1]\to {\mathbb{S}}^1$ 为标准的商映射, $o=q(0)=q(1)$. 则一个基于 $x$ 的回路等价于一个保持基点的连续映射 $l:({\mathbb{S}}^1,o)\to (X,x)$.
$\diamond$	若 $c$ 是从 $x$ 到 $x^{\prime }$ 的道路, 它的相反道路是 $$t\mapsto c(1-t):[0,1]\to X.$$它是从 $x^{\prime }$ 到 $x$ 的道路;
$\diamond$	基于 $x\in X$ 的常值道路 是指常数映射 $t\mapsto x:[0,1]\to X$.

定义 7.3.1. 拓扑空间上两条道路 $c_0$, $c_1$ 之间的一个道路同伦 (path homotopy) (或严格同伦 (strict homotopy)) 是一个同伦 $$\sigma :[0,1]\times [0,1]\to X,$$它还满足 $$\sigma (0,t)=c_0(0)=c_1(0),\sigma (1,t)=c_0(1)=c_1(1).$$特别地, $c_0$ 和 $c_1$ 有相同的出发点和终点. 如果 $c_0$ 与 $c_1$ 道路通伦, 我们用记号 $c_0{\simeq }_p{c}_1$ 表示.

如果用 ${\Lambda }_{x,y}(X)$ 表示一切从 $x$ 出发, 终于 $y$ 的 $X$ 上的道路. 则道路同伦给出了 ${\Lambda }_{x,y}(X)$ 上一个等价关系.

定义 7.3.2. 令 $\alpha$, $\beta$ 为两个 拓扑空间 $X$ 上的道路, 满足 $\alpha (1)=\beta (0)$. 定义它们的乘积道路为 $$(\alpha \ast \beta )(t)=\{\begin{array}{ll}\alpha (2t)& \text{ if }0\le t\le 1/2,\\ \beta (2t-1)& \text{ if }1/2\le t\le 1.\end{array}$$

命题 7.3.3. 令 $c$ 为拓扑空间 $X$ 上的道路. 则 $c^{-}\ast c$ 道路同伦于基于 $c(1)$ 的常值道路.

证明. 令 ${\gamma }_s(t)=c((1-s)t)$. 则 $$F(t,s)={\gamma }_s^{-}(t)\ast {\gamma }_s(t).$$给出了所需的同伦.

$■$

命题 7.3.4. 令 $\alpha$ 与 $\beta$ 为拓扑空间 $X$ 满足 $\alpha (1)=\beta (0)$ 的道路. 假设有道路 ${\alpha }^{\prime }$, ${\beta }^{\prime }$ 满足 $$\alpha {\simeq }_p{\alpha }^{\prime },\beta {\simeq }_p{\beta }^{\prime }.$$则 $\alpha \ast \beta {\simeq }_p{\alpha }^{\prime }\ast {\beta }^{\prime }$.

证明. 令 $F:\alpha {\simeq }_p{\alpha }^{\prime }$ 为 $\alpha$ 与 ${\alpha }^{\prime }$ 之间的同伦; $G:\beta {\simeq }_p{\beta }^{\prime }$ 为 $\beta$ 与 ${\beta }^{\prime }$ 之间的同伦. 定义 $$H(s,t)=\{\begin{array}{ll}F(2s,t)& \text{ if }0\le s\le 1/2,\\ G(2s-1,t)& \text{ if }1/2\le s\le 1.\end{array}$$则 $H$ 给出了所需同伦.

$■$

命题 7.3.5. 令 $\alpha ,\beta$ 与 $\gamma$ 为拓扑空间 $X$ 上的三条道路. 假设 $\alpha (1)=\beta (0)$, $\beta (1)=\gamma (0)$. 则有 $$\alpha \ast (\beta \ast \gamma ){\simeq }_p(\alpha \ast \beta )\ast \gamma .$$

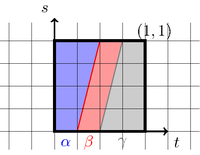
证明. 这个可以通过图 1 看出来.

图 1: ${\pi }_1$ 的结合律

作为练习, 读者应该试着把确切的公式写下来.

$■$

定义 7.3.6. 对于拓扑空间 $X$, 令 ${\varpi }_{x,y}(X)={\Lambda }_{x,y}(X)/{\simeq }_p$, 即 $x$ 到 $y$ 的道路的道路同伦类. 则上面的讨论说明, 对任何的 $x,y,z\in X$, 道路的乘积给出了良好定义的映射 $${\varpi }_{x,y}(X)\times {\varpi }_{y,z}(X)\mapsto {\varpi }_{x,z}(X),([c],[c^{\prime }])\mapsto [c]\cdot [c^{\prime }]=[c\ast c^{\prime }].$$并且这个映射满足 “结合律” $(\alpha \cdot \beta )\cdot \gamma =\alpha \cdot (\beta \cdot \gamma )$.

若 $\delta =[c]\in {\varpi }_{x,y}(X)$, 则它相反道路的道路同伦类满足 $$\delta \cdot [c^{-}]=[1_y],[c^{-}]\cdot \delta =[1_x].$$因此, 我们用形象的记号 ${\delta }^{-1}$ 来表示道路同伦类 $[c^{-}]$.

特别地, 回路之间的同伦类的乘积给出了集合 $${\pi }_1(X,x)={\varpi }_{x,x}(X)$$上一个满足结合律的二元关系, 这个二元关系给出了一个群运算: 常值道路是群的单位元, 而相反道路提供了逆元. 群 ${\pi }_1(X,x)$ 叫做带基点的空间 $(X,x)$ 的基本群 (fundamental group), 或 Poincaré 群.

我们称一个道路连通拓扑空间为道路单连通 (simply connected by paths) 的, 如果对任何 $x\in X$, 有 ${\pi }_1(X,x)=\{1\}$ 是平凡群.

7.4基本群的初步性质

对基点的依赖

命题 7.4.1. 令 $X$ 为道路连通拓扑空间. 则对任何 $x,y\in X$, 基本群 ${\pi }_1(X,x)$ 与 ${\pi }_1(X,y)$ 是同构的.

证明. 考虑 $X$ 上三个点 $x,y,z$. 令 $\delta \in {\varpi }_{y,z}(X)$. 则映射 $$\gamma \mapsto \gamma \cdot \delta :{\varpi }_{x,y}(X)\to {\varpi }_{x,z}(X)$$是同构, 它的逆是 $\gamma \mapsto \gamma \cdot {\delta }^{-1}:{\varpi }_{x,z}(X)\to {\varpi }_{x,y}(X)$. 类似地, 通过选择 ${\varpi }_{x,y}(X)$ 的元素 $\eta$ 可以给出同构 $$\gamma \mapsto {\eta }^{-1}\cdot \gamma :{\varpi }_{x,z}(X)\to {\varpi }_{y,z}(X).$$因此对 $\delta \in {\varpi }_{x,y}(X)$, 映射 $$\hat{\delta }:{\pi }_1(X,y)\to {\pi }_1(X,x),\gamma \mapsto \delta \cdot \gamma \cdot {\delta }^{-1}.$$是复合 $${\varpi }_{y,y}(X)\stackrel{\delta \cdot }{\to }{\varpi }_{y,x}(X)\stackrel{\cdot {\delta }^{-1}}{\to }{\varpi }_{x,x}(X),$$因此是一一映射, 而 $\hat{\delta }$ 显然是群同态.

$■$

系 7.4.2. 设 $X$ 是拓扑空间. 则下面的陈述等价.

$\diamond$	${\pi }_1(X,x)$ 是平凡群.
$\diamond$	任何两条始于 $x$ 且具有相同终点的道路都严格地同伦.
$\diamond$	任何基于 $x$ 的回路都严格同伦于基于 $x$ 的常值道路.

例 7.4.3. 考虑空间 ${\mathbb{R}}^n$. 对任何基于原点的回路 $l:{\mathbb{S}}^1\to {\mathbb{R}}^n$, 定义 $L:{\mathbb{S}}^1\times [0,1]\to {\mathbb{R}}^n$, $L(\theta ,t)=(1-t)\cdot l(\theta )$. 则 $L$ 就是一个从回路 $l$ 到基于原点的常值道路的严格同伦. 因此对一切 $x\in {\mathbb{R}}^n$, 我们有 ${\pi }_1({\mathbb{R}}^n,x)=\{1\}$.

注 7.4.4.

1.	如果 $\delta ,\eta$ 是两个道路同伦类, 且 $\delta \cdot \eta$ 有意义 ($\delta$ 和 $\eta$ 由首尾相连的道路代表), 那么 $\widehat{\delta \eta }=\hat{\delta }\circ \hat{\eta }$.
2.	如果取不同的两个元素 $\delta ,{\delta }^{\prime }\in {\varpi }_{x,y}(X)$, 则同构 $\hat{\delta }$ 与 $\widehat{{\delta }^{\prime }}$ 未必相同. 因此, 虽然不同基点的基本群是同构的, 但却不是 “典则同构” 的.

函子性质

设 $f:X\to Y$ 为拓扑空间之间的连续映射. 对 $X$ 上连结两点 $x,y$ 的道路 $c$, 复合映射 $f\circ c$ 是 $Y$ 上连结 $f(x)$ 与 $f(y)$ 的道路. 根据命题 7.1.3 (的关于严格同伦的变体), $f$ 诱导了集合之间的映射$${\varpi }_{x,y}(f):{\varpi }_{x,y}(X)\to {\varpi }_{f(x),f(y)}(Y).$$由于$$f\circ (c\ast d)=(f\circ c)\ast (f\circ d),$$映射 ${\varpi }_{x,y}(f)$ 尊重严格同伦类的毗连, 即$${\varpi }_{x,z}(f)(\gamma \delta )=({\varpi }_{x,y}(f)(\gamma ))({\varpi }_{y,z}(f)(\delta )).$$特别地, 如果 $x=y$, 我们就得到了基本群之间的同态$${\pi }_1(f,x):{\pi }_1(X,x)\to {\pi }_1(Y,f(x)).$$在不至于引起误会的前提下, 这个同态通常被简写为 $f_{\ast }$. 如果 $f:X\to Y$, $g:Y\to Z$ 是两个连续映射, 那么 作为从 ${\pi }_1(X,x)$ 到 ${\pi }_1(Z,g(f(x)))$ 的同态, 成立$$(g\circ f{)}_{\ast }=g_{\ast }\circ f_{\ast }.$$特别地, 如果 $f$ 是同胚, 那么 $f_{\ast }$ 是群的同构.

然而基本群不仅仅是同胚的不变量, 它还是同伦的不变量. 更准确的说法是下面的命题.

命题 7.4.5. 令 $X$ 与 $Y$ 是两个拓扑空间, $f_0$, $f_1$ 是两个由 $X$ 到 $Y$ 的连续映射, 并且可以通过同伦 $\sigma :X\times [0,1]\to Y$ 相连. 令 $x\in X$, $y_0=f_0(x)$, $y_1=f_1(x)$, 以及 $\delta =[\sigma (x,\cdot )]\in {\varpi }_{y_0,y_1}(Y)$. 则 $$\hat{\delta }\circ {\pi }_1(f_1,x)={\pi }_1(f_0,x).$$

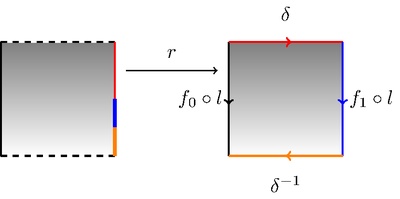
证明. 令 $\gamma$ 为 ${\pi }_1(X,x)$ 中的一个严格同伦类, 由道路 $l:[0,1]\to X$ 代表. 则复合映射 $\tau =\sigma \circ (l\times {\mathrm{I}\mathrm{d}}_{[0,1]})$ 给出了回路 $f_0\circ l$ 与回路 $f_1\circ l$ 的同伦. 今构造正方形 $[0,1]\times [0,1]$ 与商空间 $\frac{[0,1]\times [0,1]}{[0,1]\times \{0,1\}}$ 的如图 2 所示的同胚: 虚线部分要被坍缩掉, 而左侧具有某种颜色的部分要被同胚地映射到具有相同颜色的地方 (具体同胚留给读者构造).

图 2: 同伦与固定基点的同伦

记映射 $[0,1]\times [0,1]\to \frac{[0,1]\times [0,1]}{[0,1]\times \{0,1\}}\cong [0,1]\times [0,1]$ 为 $r$. 则映射 $\tau \circ r$ 就给出了想要的同伦.

$■$

系 7.4.6. 令 $f_0,f_1$ 是从带基点的拓扑空间 $(X,x)$ 到 $(Y,y)$ 的保持基点的连续映射. 如果存在一个保持基点的同伦连结 $f_0$ 与 $f_1$, 那么作为基本群 ${\pi }_1(X,x)$ 和 ${\pi }_1(Y,y)$ 之间的同态, 成立 $f_{0\ast }=f_{1\ast }$.

$■$

系 7.4.7. 若连续映射 $f$ 是从拓扑空间 $X$ 到拓扑空间 $Y$ 的一个同伦等价, 那么 $f_{\ast }:{\pi }_1(X,x)\to {\pi }_1(Y,f(x))$ 是同构.

证明. 令 $g$ 是 $f$ 的同伦逆. 令 $\delta \in {\varpi }_{x,g(f(x))}$. 则映射 $g_{\ast }\circ f_{\ast }:{\pi }_1(X,x)\to {\pi }_1(X,g(f(x)))$ 与 $\hat{\delta }$ 相等. 因此 $g_{\ast }\circ f_{\ast }$ 是同构, 故而 $f_{\ast }$ 是单同态, $g_{\ast }$ 是满同态. 更换 $f,g$ 之间的角色就证明了命题.

$■$

系 7.4.8. 若 $X$ 同伦等价于单点集合, 则 ${\pi }_1(X,x)$ 是平凡群.

$■$

自由同伦的回路

定义 7.4.9. 我们称拓扑空间 $X$ 上的两个回路 $c_0:[0,1]\to X$, $c_1:[0,1]\to X$ 是自由同伦 (freely homotopic) 的, 如果存在同伦 $$\sigma :[0,1]\times [0,1]\to X,$$满足 $\sigma (t,0)=c_0(t)$, $\sigma (t,1)=c_1(t)$, $\sigma (0,s)=\sigma (1,s)$. 即, 对任何 $s\in [0,1]$, 道路 $\sigma (t,s)$ 是回路.

通过商映射 $[0,1]\to {\mathbb{S}}^1$, 我们可以将任何回路看作从 ${\mathbb{S}}^1$ 到 $X$ 的连续映射. 若用 $o$ 代表 $0$ 在 ${\mathbb{S}}^1$ 中的像, 那么基于 $x\in X$ 的两个回路固定基点地同伦相当于它们在集合 $[({\mathbb{S}}^1,o);(X,x)]$ 中是同一个元素; 而它们自由同伦则是在说它们在集合 $[{\mathbb{S}}^1;X]$ 中是同一个元素. 在这一小段中, 我们来澄清固定基点同伦类和自由同伦类的关系.

命题 7.4.10. 令 $X$ 为道路连通的拓扑空间, $x$ 是 $X$ 上的点. 则 $X$ 上任何的回路都自由地同伦于一个基于 $x$ 的回路.

证明. 令 $c$ 为 $X$ 上的一条回路, $c(0)=y$. 令 $d$ 为从 $x$ 到 $y$ 的一条道路. 我们断言基于 $x$ 的道路 $d\ast c\ast d^{-1}$ 与 $c$ 自由同伦, 它们之间的一个同伦由 $$\sigma (s,t)=d_s\ast c\ast d_s^{-},$$给出, 这里 $d_s(t)=d(st)$. 我们留给读者验证这个同伦的连续性.

$■$

命题 7.4.11. 设 $X$ 为拓扑空间, $x$ 是 $X$ 上的点. 令 $c_0$ 和 $c_1$ 为两个基于 x 的回路. 则 $c_0$ 与 $c_1$ 自由同伦的必要且充分条件是存在 $\delta \in {\pi }_1(X,x)$, 使得 $[c_0]=\delta [c_1]{\delta }^{-1}$.

证明. 充分性已经在上一段的证明里说明了. 现在假设 $c_0$ 与 $c_1$ 通过 $\sigma :[0,1]\times [0,1]\to X$ 自由同伦. 令 $d$ 为道路 $s\mapsto \sigma (0,s)$. 根据自由同伦的定义, $s\mapsto \sigma (1,s)$ 也是道路 $d$. 再度应用图 2 所示的映射 $r$, 就得到了 $c_0$ 与 $d\ast c_1\ast d^{-}$ 之间固定基点的同伦.

$■$

系 7.4.12. 令 $X$ 为拓扑空间. 则 $[{\mathbb{S}}^1;X]$ 是单点集合的必要充分条件为 $X$ 道路连通, 并且对任何 $x\in X$, ${\pi }_1(X,x)=\{1\}$.

$■$

积空间的基本群

命题 7.4.13. 设 $(X_i,x_i{)}_{i\in I}$ 是一族带基点的拓扑空间. $X={\prod }_{i\in I}{X}_i$, 以 $x=(x_i{)}_{i\in I}$ 为基点. 则 ${\pi }_1(X,x)$ 同构于乘积群 ${\prod }_{i\in I}{\pi }_1(X_i,x_i)$.

证明. 根据乘积空间的泛性质, 给出一条 $X$ 上的道路 $c:[0,1]\to X$ 等价于给出一族道路 $c_i:[0,1]\to X_i$, 其中 $c_i(0)$ ($c_i(1)$) 为 $c(0)$ ($c(1)$) 的第 $i$ 个分量. 因此对 $X$ 上两个点 $x=(x_i)$, $y=(y_i)$, 自然的映射 ${\prod }_{i\in I}{\varpi }_{x_i,y_i}(X_i)\to {\varpi }_{x,y}(X)$ 是满射. 类似地, 给出 $X$ 上道路 $c$, $d$ 的严格同伦等价于对每个 $i\in I$ 给出 $X_i$ 上道路 $c_i$, $d_i$ 的严格同伦. 因此, 满射 ${\prod }_{i\in I}{\varpi }_{x_i,y_i}(X_i)\to {\varpi }_{x,y}(X)$ 是同构. 取 $x=y$ 就推出了本命题.

$■$

7.5球面的基本群

命题 7.5.1.

1.	去掉原点的平面 ${\mathbb{R}}^2\setminus \{0\}$ 上任意两条自由同伦的回路有相等的环绕数.
2.	回路的环绕数给出了群同构 ${\pi }_1({\mathbb{R}}^2\setminus \{0\})\to \mathbb{Z}$.

证明. 首先我们需要说明环绕数在道路的自由同伦类上是常值. 事实上, 我们来证明定义 6.4.1 中的 “接近” 与自由同伦是同一个概念. 按照那里的论证, 由于非常接近的回路可以通过线段互相形变, 接近的回路是自由同伦的. 设 $\sigma :[0,1]\times [0,1]\to {\mathbb{R}}^2\setminus \{0\}$ 为从回路 $l_0:[0,1]\to {\mathbb{R}}^2\setminus \{0\}$ 到回路 $l_1:[0,1]\to {\mathbb{R}}^2\setminus \{0\}$ 的自由同伦. 由于 $\sigma$ 连续, ${\mathbb{R}}^2\setminus \{0\}$ 的所有凸开集关于 $\sigma$ 的逆像构成了 ${\mathbf{S}}^1\times [0,1]$ 的覆盖. 根据 Lebesgue 数引理, 命题 6.2.4, 存在方形的分割 $$0=a_1<\dots <a_{n-1}<a_n=1,0=b_1<\dots <b_{n-1}<b_n=1,$$使得每个小方形 $q([a_i,a_{i+1}])\times [b_j,b_{j+1}]$ 在 $\sigma$ 下的像都落入某个 ${\mathbb{R}}^2\setminus \{0\}$ 的凸开集中. 特别地, 回路 $l_{b_j}(t)=\sigma (t,b_j)$ 与 $l_{b_{j+1}}$ 在定义 6.4.1 的意义下非常接近. 从而 $l_0$ 与 $l_1$ 接近. 这就证明了第一个断言.

第二个断言的证明. 对任何两条基点为 $(1,0)$ 的可微回路 $l_1$, $l_2$, 微积分换元公式告诉我们 ${\int }_{l_1\ast l_2}\omega ={\int }_{l_1}\omega +{\int }_{l_2}\omega$. 由于命题 6.4.2 告诉我们任何固定基点的同伦类都可以由可微映射代表, 上面的公式就说明环绕数给出了群同态.

这是一个满同态, 因为 $t\mapsto (\cos (2\pi nt),\sin (2\pi nt))$ 的环绕数是 $n$.

设 $l$ 是一个基点为 $(1,0)$ 的可微的回路, 环绕数是 $0$. 则函数 $$\theta (t)={\int }_{l{|}_{[0,t]}}\omega$$是一个从 $[0,1]$ 到 $\mathbb{R}$ 的基于 $0$ 的回路. 定义 $$\sigma (t,s)=|(1-t)l(s)+t|\cdot (\cos (s\theta (t)),\sin (s\theta (t))).$$这是一个从 $[0,1]\times [0,1]$ 到 ${\mathbb{R}}^2\setminus \{0\}$ 的连续映射, 提供了回路 $l$ 和基于 $(1,0)$ 的常值回路的严格同伦 (见公式 (6.1)). 这就证明了环绕数给出了单同态, 从而完成了命题的证明.

$■$

由于 ${\mathbb{S}}^1$ 是 ${\mathbb{R}}^2\setminus \{0\}$ 的一个形变收缩核 (见 7.1.4/3), 系 7.4.7 推出如下结论.

系 7.5.2. 圆周 ${\mathbb{S}}^1$ 的基本群同构于整数加法群 $\mathbb{Z}$.

$■$

为了计算 ${\mathbb{S}}^n$ 的基本群, 我们先证明下述结论, 它是接下来要证明的 Seifert–van Kampen 定理的特殊情形.

命题 7.5.3. 设 $U_1$, $U_2$ 为拓扑空间 $X$ 的两个道路连通, 道路单连通开集. 若 $X=U_1\cup U_2$, 且 $U_1\cap U_2$ 道路连通, 那么 $X$ 是道路连通且道路单连通的拓扑空间.

注意: 在使用这个命题时, 不能将 “开集” 换做 “闭集”. 一个反例由所谓的 “Griffiths 孪锥” 提供.

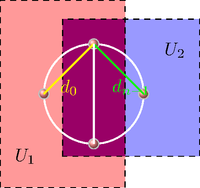
若 $n\ge 2$, 则 ${\mathbb{R}}^{n+1}$ 中的单位球面 ${\mathbb{S}}^n$ 可以由两个同胚于 ${\mathbb{R}}^n$ 的开集$$\begin{array}{rl}U& ={\mathbb{S}}^n\setminus \{(0,\dots ,0,1)\},\\ V& ={\mathbb{S}}^n\setminus \{(0,\dots ,0,-1)\}\end{array}$$覆盖, 并且 $U\cap V\cong {\mathbb{R}}^n\setminus \{0\}$ 道路连通. 根据命题 7.5.3, 我们得到如下结论.

系 7.5.4. 若 $n\ge 2$, ${\pi }_1({\mathbb{S}}^n)\cong \{1\}$.

$■$

根据命题 7.4.13, 环面 ${\mathbb{S}}^1\times {\mathbb{S}}^1$ 的基本群同构于加法群 ${\mathbb{Z}}^2$. 因此, 环面与球面不同胚.

命题 7.5.3 的证明. 令 $x\in U_1\cap U_2$. 则利用 $U_i$ 的道路连通性可知任意 $x^{\prime }\in U_i$ 都可以与 $x$ 通过道路相连. 于是 $X=U_1\cup U_2$ 是道路连通的.

令 $c:[0,1]\to X$ 为一条基于 $x\in U_1\cap U_2$ 的回路. 利用 Lebesgue 数引理 (命题 6.2.4), 存在 $[0,1]$ 的分划 $$0=a_1<a_2<\cdots <a_n=1,$$使得 $c([a_i,a_{i+1}])$ 要么完全落在 $U_1$ 中, 要么完全落在 $U_2$ 中. 令 $x_i=c(a_i)$. 令 $c_i$ 为一条从 $x$ 出发到 $x_i$ 中止的道路. 如果 $x_i\in U_1\cap U_2$, 我们要求 $c_i$ 也完全落入 $U_1\cap U_2$ 中. 令 $d_i(t)=c((1-t)a_i+t{a}_{i+1})$, 则 $$[c]=[d_0\ast \cdots \ast d_{n-1}],$$并且对任何的 $i$, 回路 $c_i\ast d_i\ast c_{i+1}^{-}$ 的像要么完全落入 $U_1$, 要么完全落入 $U_2$. 由于 $U_i$ 是道路单连通的, 它必须严格同伦于基于 $x$ 的常值道路. 同理, $d_0$ 严格同伦于 $c_1$.

图 3: 逐次取消回路

因此 $$\begin{array}{rl}[c]& =[d_0\ast d_1\ast \cdots \ast d_{n-1}]\\ & =[c_1\ast d_1\ast \cdots \ast d_{n-1}]\\ & =[c_2\ast d_2\ast \cdots \ast d_{n-1}]\\ & ⋮\\ & =[c_{n-1}\ast d_{n-1}].\end{array}$$由于 $c_{n-1}$ 与 $d_{n-1}$ 的起始点相反, 并且都落入某个道路单连通空间, 它们的乘积是严格同伦于常值道路的. 这就完成了证明.

$■$

Jordan 分离定理

定理 7.5.5. 令 $C$ 为 ${\mathbb{R}}^2$ 中同胚于 ${\mathbb{S}}^1$ 的子空间. 则 ${\mathbb{R}}^2\setminus C$ 不连通.

我们将展示的证明属于 P. H. Doyle. 下面所处理的空间都是局部道路连通的, 所以探讨连通性和道路连通性没有差别, 我们不再嘱咐读者了.

第一步, 我们将 ${\mathbb{R}}^2$ 看作 ${\mathbb{S}}^2$ 去掉一点而得到的子空间 (比如利用球极投影). 下面的命题说明, 只需证明 ${\mathbb{S}}^2\setminus C$ 是不连通的.

命题 7.5.6. ${\mathbb{S}}^2\setminus C$ 和 ${\mathbb{R}}^2\setminus C$ 的连通分支数一样多.

证明留作习题.

第二步, 选择 $P\in C$. 利用 $P$ 处球极投影, 我们可以将 $C\setminus \{P\}$ 同胚地映射成 ${\mathbb{R}}^2$ 的同胚于 $\mathbb{R}$ 的闭子空间 $A$, 于是 ${\mathbb{S}}^2\setminus C$ 同胚于 ${\mathbb{R}}^2\setminus A$. 因此, 只需证明 ${\mathbb{R}}^2$ 挖掉一个同胚于 $\mathbb{R}$ 的闭子空间之后不连通. 为此, 我们用反证法, 假设 ${\mathbb{R}}^2\setminus A$ 连通.

证明的要点是将 ${\mathbb{R}}^2$ 看作 ${\mathbb{R}}^3$ 的由 $z=0$ 定义的子空间, 并且考察 ${\mathbb{R}}^3\setminus A$ 的基本群. 我们利用两种方法来计算 ${\pi }_1({\mathbb{R}}^3\setminus A)$.

方法一: 利用命题 7.5.3 直接计算. 令$$U_{+}=\{(x,y,z)\in {\mathbb{R}}^3:z>-1\}\setminus (A\times ]-1,0]),$$以及$$U_{-}=\{(x,y,z)\in {\mathbb{R}}^3:z<1\}\setminus (A\times [0,1[).$$则 $U_{+}\cup U_{-}={\mathbb{R}}^3\setminus A$. 利用直线同伦, 可以看出 $\{(x,y,\pm 1):(x,y)\in {\mathbb{R}}^2\}$ 分别是 $U_{\pm }$ 的形变收缩核. 因此, $U_{\pm }$ 可缩. 类似地, $U_{+}\cap U_{-}$ 以 ${\mathbb{R}}^2\setminus A$ 为形变收缩核. 因此, 若 ${\mathbb{R}}^2\setminus A$ 连通, 那么 ${\mathbb{R}}^3\setminus A$ 道路单连通.

方法二: 利用 ${\mathbb{R}}^3$ 的自同胚将 $A$ 化成 “好” 的形式后直接计算. 事实上, 我们来构造一个 ${\mathbb{R}}^3$ 的自同胚 $\phi$, 使得 $\phi (A)$ 是 $z$-轴 $Z$. 如果这件事情完成了, 就有 ${\pi }_1({\mathbb{R}}^3\setminus A)={\pi }_1({\mathbb{R}}^3\setminus Z)$, 而 ${\mathbb{R}}^3\setminus Z$ 同伦等价于 ${\mathbb{S}}^1$, 故而基本群是 $\mathbb{Z}$. 这就与方法一中的计算矛盾. 从而 Jordan 的定理得证.

因此证明的最后一步就是找到上面的同胚. 固定同胚 $f:A\to \mathbb{R}$, 记它的逆映射为 $r\mapsto (u(r),v(r))$. 利用 Tietze 扩张定理, 可以把 $f$ 扩张成连续映射 $g:{\mathbb{R}}^2\to \mathbb{R}$. 定义$${\psi }_1(x,y,z)=(x,y,z+g(x,y)).$$则 ${\psi }_1$ 显然是同胚. ${\psi }_1(A)$ 与每个平面 $z=z_0$ 都只交一个点 $(u(z_0),v(z_0),z_0)$. 利用这个观察, 定义同胚$${\psi }_2(x,y,z)=(x-u(z),y-v(z),z).$$则 $\phi ={\psi }_2\circ {\psi }_1$ 即为所求.

事实上, ${\mathbb{R}}^2\setminus C$ 恰好有两个连通分支 (“Jordan 曲线定理”). 上述论证完全可以推出这个定理, 但需要借助命题 7.5.3 的升级版本: 假如 $U$, $V$ 是局部道路连通拓扑空间 $X$ 的道路单连通开集, $X=U\cup V$, 则 ${\pi }_1(X)$ 同构于 由 ${\pi }_0(U\cap V)$ 去掉一个元素后生成的自由群. 我们会在讲解一般 van Kampen 定理时处理上面的断言.

7.6箭图与广群

这一节我们介绍一些代数结构.

定义 7.6.1. 一个箭图 (quiver) 是一个四元集合 $(S,F,o,t)$, 其中 $S$ 是一个集合, 其中的元素叫做箭图的 “顶点”, $F$ 是一个集合, 其中的元素叫做箭图的 “箭头”, $o,t$ 是两个从 $F$ 到 $S$ 的映射. 对于箭头 $f$, $o(f)$ 叫做 $f$ 的起点, $t(f)$ 叫做箭头的终点. 下图描绘了一个有两个顶点, 四个箭头的箭图: 对于箭图 $C=(S,F,o,t)$, 有时用 $\mathrm{S}\mathrm{o}\mathrm{m}(C)$, $\mathrm{F}\mathrm{l}(C)$, $o_C$, $t_C$ 来分别代表 $S,F,o,t$. 对任意两个顶点 $a,b\in \mathrm{S}\mathrm{o}\mathrm{m}(C)$, 我们用记号 $C_{a,b}$ 来代表集合 $$\{f\in \mathrm{F}\mathrm{l}(C):o(f)=a,t(f)=b\}.$$

定义 7.6.2. 令 $C=(S,F,o,t)$ 为一个箭图. 令 $J$ 为 $F\times F$ 的子集, 它包含了一切偶对 $(f,g)$, 满足 $t(f)=o(g)$. $C$ 上的合成法则 (composition law) 是指一个从 $J$ 到 $F$ 的映射 $m$, 它对任何满足 $t(f)=o(g)$ 的箭头 $f,g\in F$, 指定了一个箭头 $m(f,g)\in F$.

我们称合成法则满足结合律, 如果对任意 $(f,g)\in J$, $(g,h)\in J$, 成立 $$m(m(f,g),h)=m(f,m(g,h)).$$

我们称箭头 $e_b\in C_{b,b}$ 是合成法则 $m:J\to F$ 的幺元, 如果对任何 $a$, 任何 $f\in C_{a,b}$, 任何 $g\in C_{b,a}$, 有 $m(f,e_b)=f$, $m(e_b,g)=g$.

定义 7.6.3. 一个范畴 (category) 是一个偶对 $(C,m)$, 其中 $C$ 是一个箭图, $m$ 是 $C$ 上满足结合律的合成法则, 并且对任何 $a\in \mathrm{S}\mathrm{o}\mathrm{m}(C)$, $C_{a,a}$ 中有幺元. 在一个范畴中, 我们通常将 $m(f,g)$ 记做 $f\cdot g$ 或者毗联 $fg$ (或者 $g\circ f$, 注意顺序是相反的).

一个从范畴 $C$ 到范畴 $C^{\prime }$ 的函子 (functor) 是一个偶对 $(u,v)$, 其中 $u$ 是从 $\mathrm{S}\mathrm{o}\mathrm{m}(C)$ 到 $\mathrm{S}\mathrm{o}\mathrm{m}(C^{\prime })$ 的映射, $v$ 是从 $\mathrm{F}\mathrm{l}(C)$ 到 $\mathrm{F}\mathrm{l}(C^{\prime })$ 的映射, 满足

$\diamond$	$o_{C^{\prime }}\circ v=u\circ o_C$,
$\diamond$	$t_{C^{\prime }}\circ v=u\circ t_C$,
$\diamond$	如果 $f\in C_{a,b}$, $g\in C_{b,c}$, 那么在 $C_{u(a),u(c)}^{\prime }$ 中成立等式 $$v(f\cdot g)=v(f)\cdot v(g).$$

一个广群 (groupoid, 或译为 “群胚”) 是一个范畴 $G$, 它满足如下性质: 对任意 $f\in G_{a,b}$, 存在 $g\in G_{b,a}$, 满足 $fg=e_a$, $gf=e_b$. 如果 $G$ 是一个广群, 那么对 $G$ 的顶点 $a$, 集合 $G_{a,a}$ 是一个群.

例 7.6.4 (基本广群). 令 $X$ 是拓扑空间. 令 $F={\coprod }_{x,y\in X}{\varpi }_{x,y}(X)$. 定义 $o:F\to X$ 为满足 $o({\varpi }_{x,y}(X))=x$ 的映射. 类似地, 定义 定义 $t:F\to X$ 为满足 $t({\varpi }_{x,y}(X))=y$ 的映射. 则 $\varpi (X)=(X,F,o,t)$ 构成了一个箭图. 道路的同伦类的复合给出了一个 $\varpi (X)$ 上的合成法则. 在这个合成法则下, $\varpi (X)$ 构成了一个广群, 叫做 $X$ 的基本广群 (fundamental groupoid), 或 Poincaré 广群.

例 7.6.5 (置换广群). 令 $p:X\to S$ 是集合之间的映射. 对 $a\in S$, 令 $X_a=p^{-1}(a)$; 对 $a,b\in S$, 令 $G_{a,b}=\mathcal{B}(X_a;X_b)$ 为一切从 $X_a$ 到 $X_b$ 的双射. 令 $\mathrm{S}\mathrm{o}\mathrm{m}(G)=S$, $\mathrm{F}\mathrm{l}(G)={\coprod }_{(a,b)\in S\times S}{G}_{a,b}$, $o_G(G_{a,b})=\{a\}$, $t_G(G_{a,b})=\{b\}$, 则 $G=(\mathrm{S}\mathrm{o}\mathrm{m}(G),\mathrm{F}\mathrm{l}(G),o_G,t_G)$ 是一个广群. 对于 $f\in G_{a,b}$, $g\in G_{b,c}$, 它们的合成法则由映射的复合给出: $$m(f,g)=g\circ f.$$广群 $(G,m)$ 叫做 $X$ 相对于 $p$ 的置换广群 (permutation groupoid), 通常记作 $\mathcal{B}(X,p)$.

一个广群 $G$ 在 $X$ 上相对于 $p$ 的右作用是一个广群态射 $$\mu :G\to \mathcal{B}(X,p).$$于是对于可复合的 $f,g\in \mathrm{F}\mathrm{l}(G)$, 成立 $\mu (fg)=\mu (g)\circ \mu (f)$.

7.7习题

7.7.1. 证明, 如果拓扑空间 $X$ 与 拓扑空间 $Y$ 同伦等价, $Y$ 与 拓扑空间 $Z$ 同伦等价, 那么 $X$ 与 $Z$ 同伦等价.

7.7.2. 证明 Hilbert 空间 ${\ell }^2(\mathbb{N})$ (习题 2.6.9) 的子空间 $${\mathbb{S}}^{\infty }=\left\{a\in {\ell }^2(\mathbb{N}):\sum _{n\in \mathbb{N}}|a(n){|}^2=1\right\}$$是可缩的.

7.7.3. 令 $X$ 为拓扑空间. 我们称 $X$ 的 Lyusternik–Schnirelmann 畴数 $\mathrm{c}\mathrm{a}\mathrm{t}(X)$ 为 $n$, 如果存在 $X$ 的开覆盖 $U_0,U_1,\dots ,U_n$, 其中每个包含映射 $U_i\hookrightarrow X$ 都零伦, 并且 $n$ 是最小的能够保证这样开覆盖存在的整数.

1.	拓扑空间 $X$ 的纬悬 (suspension) $\Sigma X$ 是商空间 $(X\times [0,1])/(X\times \{0,1\})$. 证明 $\mathrm{c}\mathrm{a}\mathrm{t}(\Sigma X)\le 1$, 且 $\mathrm{c}\mathrm{a}\mathrm{t}(\Sigma X)=0$ 当且仅当 $X$ 可缩.
2.	令 $X$ 为 ${\mathbb{S}}^2/\{p,q,r\}$, 其中 $p,q,r$ 是 ${\mathbb{S}}^2$ 上三个不同点. 求 $\mathrm{c}\mathrm{a}\mathrm{t}(X)$.
3.	证明 $\mathrm{c}\mathrm{a}\mathrm{t}(\mathbb{R}{\mathrm{P}}^n)\le n$. [利用一点上同调的性质可以证明, $\mathbb{R}{\mathrm{P}}^n$ 的 Lyusternik–Schnirelmann 畴数等于 $n$.]
4.	如果 $X$ 与 $Y$ 同伦等价, 则 $\mathrm{c}\mathrm{a}\mathrm{t}(X)=\mathrm{c}\mathrm{a}\mathrm{t}(Y)$.

7.7.4. 一般线性群 ${\mathrm{G}\mathrm{L}}_n(\mathbb{R})$ 同伦等价于实正交群 $\mathrm{O}(n)$; 一般线性群 ${\mathrm{G}\mathrm{L}}_n(\mathbb{C})$ 同伦等价于酉群 $\mathrm{U}(n)$.

7.7.5. 令 $C$ 为梳子空间 (例 5.6). 令 $\sigma :{\mathbb{R}}^2\to {\mathbb{R}}^2$ 为以 $(0,1)$ 为对称中心的中心对称. 证明 $C$ 可缩, 但是 $C\cup \sigma (C)$ 不可缩.

7.7.6. 下面的 (2), (3) 两款是 Bourbaki, TA III, p. 321, Exercise 1.

1.	设 $P$ 是拓扑空间 $X$ 的单点子空间. 如果 $P$ 是 $X$ 的形变收缩核, 那么存在 $P$ 的开邻域 $V$, 使得包含映射 $V\hookrightarrow X$ 是零伦的.
2.	令 $C_{\theta }$ 为 ${\mathbb{R}}^2$ 中连结 $(0,0)$ 和 $(\cos (2\pi \theta ),\sin (2\pi \theta ))$ 的线段. 证明 $\{(0,0)\}$ 是 $$C=\bigcup _{\theta \in \mathbb{Q}\cap [1/6,1/4]}{C}_{\theta }$$的形变收缩核, 但 $C$ 上任何其它点都不是 $C$ 的形变收缩核.
3.	证明 $D={\bigcup }_{n\in \mathbb{Z}}(0,n)+C$ 是可缩的, 但任何 $D$ 的点都不是 $D$ 的形变收缩核.

7.7.7. 令 $\sigma :X\times [0,1]\to X$ 为恒等映射到自己的一个同伦. 则对于任何 $X$ 上的点 $x$, 证明道路 $\delta (t)=\sigma (x,t)$ 落在 ${\pi }_1(X,x)$ 的中心里.

7.7.8 (一些空间的基本群的计算). 计算下列空间的基本群.

1.	Sierpiński 空间 (例 1.1.1/2).
2.	$\mathbb{Q}$.
3.	设 $D$ 是简约的梳子空间 (例 5.6), $P=(1,0)$ 令 $$X=D\cup (\{0\}\times [1,2])\cup ([0,1]\times \{2\})\cup (\{1\}\times [0,2]),$$赋予 ${\mathbb{R}}^2$ 的子空间拓扑. 求 ${\pi }_1(X,P)$.
4.	复射影空间 $\mathbb{C}{\mathrm{P}}^n$.

7.7.9. 令 $i:A\hookrightarrow X$ 为子空间的包含映射. 如果 $A$ 是 $X$ 的收缩核 (习题 3.8.2), 证明对任意 $a\in A$, 映射 $$i_{\ast }:{\pi }_1(A,a)\to {\pi }_1(X,a)$$是单射. 利用这个性质说明 Möbius 带的边界圆周不是 Möbius 带的收缩核.

7.7.10. 证明命题 7.5.6.

7.7.11. 对正整数 $n$, $n$ 阶正交矩阵可以看作球面 ${\mathbb{S}}^{n-1}$ 到自己的连续映射. 什么时候两个 $n$ 阶正交矩阵给出同伦的映射?

7.7.12. 这个习题致力于证明 Poincaré 的髮球定理: 任何 ${\mathbb{S}}^2$ 上的连续切向量场必然有零点.

1.	球面 ${\mathbb{S}}^2$ 上的一个连续切向量场是连续映射 $X:{\mathbb{S}}^2\to {\mathbb{R}}^3$, 满足 $X(p)\cdot p$ (向量的内积) 对任何 $p\in {\mathbb{S}}^2$ 都为零. 验证 $(x,y,z)\mapsto (-y,x,0)$ 是 ${\mathbb{S}}^2$ 上的切向量场. 找出它的零点. 在草稿纸上画一下这个向量场的模样.
2.	令 $N=(0,0,1)$, $S=(0,0,-1)$, $p_N:{\mathbb{S}}^2\setminus \{N\}\to {\mathbb{R}}_N^2$, $p_S:{\mathbb{S}}^2\setminus \{S\}\to {\mathbb{R}}_S^2$ 分别为从 $N$ 和 $S$ 出发的球极投影 (用平面 $z=0$ 来承接投影, 下标中的 $N$, $S$ 只是为了区别到达域). 定义 $\phi :{\mathbb{R}}_N^2\setminus \{(0,0)\}\to {\mathbb{R}}_S^2\setminus \{(0,0)\}$, $$\phi (x,y)=\left(\frac{x}{x^2+y^2},\frac{y}{x^2+y^2}\right).$$利用多变量微分学里学到的概念, 解释为何 ${\mathbb{S}}^2$ 上的连续切向量场等价于两个连续 (列) 向量值函数 $X_N:{\mathbb{R}}_N^2\to {\mathbb{R}}^2$, $X_S:{\mathbb{R}}_S^2\to {\mathbb{R}}^2$, 满足 $$X_S(\phi (x,y))=\left[\begin{array}{cc}\frac{y^2-x^2}{(x^2+y^2{)}^2}& \frac{-2xy}{(x^2+y^2{)}^2}\\ \frac{-2xy}{(x^2+y^2{)}^2}& \frac{x^2-y^2}{(x^2+y^2{)}^2}\end{array}\right]\cdot X_N(x,y).$$(如果没学过多变量微分学有关内容, 读者也可以用这一款的描述来定义切向量场.)
3.	令 $E$ 为球面 ${\mathbb{S}}^2$ 的赤道 (球面上坐标 $z=0$ 的点). 证明, 如果连续切向量场 $X$ 没有零点, 那么 $X_S{|}_{p_S(E)}$ 与 $X_N{|}_{p_N(E)}$ 看作映射 ${\mathbb{S}}^1\to {\mathbb{R}}^2\setminus \{0\}$ 都是零伦的.
4.	验证向量值函数 $$\left[\begin{array}{cc}\frac{y^2-x^2}{(x^2+y^2{)}^2}& \frac{-2xy}{(x^2+y^2{)}^2}\\ \frac{-2xy}{(x^2+y^2{)}^2}& \frac{x^2-y^2}{(x^2+y^2{)}^2}\end{array}\right]\cdot \left[\begin{array}{c}1\\ 0\end{array}\right]$$在 $p_S(E)$ 上的限制具有环绕数 $-2$, 从而推出 Poincaré 的定理.

脚注

1.	It is not enough, in fact, for a science to be legitimate; its utility must be incontestable. So many objects demand our attention that only the most important have the right to be considered.