10. 基本群 (III): van Kampen 定理

定理的历史 (A. Gramain, “Le théorème de Van Kampen”). Cet énoncé a été démontré en 1931 par H . SEIFERT, non pour des ouverts $U_1$ et $U_2$, mais pour des sous-complexes d’un complexe simplicial $Y$. En 1933, E. VAN KAMPEN retrouve cet énoncé comme cas particulier d’une situation plus compliquée, issue d’un pr oblème de géométrie algébrique.

10.1定理的陈述

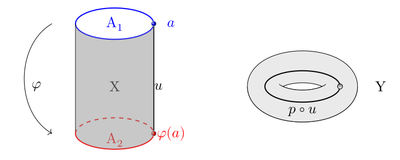
在这一小节中, 我们介绍计算基本群的一个工具, Seifert–van Kampen 定理. 我们首先固定一些记号. 令 $U_1$, $U_2$ 为拓扑空间 $X$ 的开子空间. 设:

$\diamond$	$X=U_1\cup U_2$,
$\diamond$	$U_1$, $U_2$ 道路连通, 以及
$\diamond$	$U_1\cap U_2$ 非空且道路连通.

令 $j_1:U_1\to X$, $j_2:U_2\to X$, ${\iota }_1:U_1\cap U_2\to U_1$, 与 ${\iota }_2:U_1\cap U_2\to U_2$ 为相应的包含映射.

根据基本群的 “自然性”, 下面的图表是交换的

根据自由积的泛性质, 同态 $j_{1\ast }$, $j_{2\ast }$ 给出了同态$$\rho :{\pi }_1(U_1,x_0)\ast {\pi }_1(U_2,x_0)\to {\pi }_1(X,x_0).$$它满足, 对 $i=1,2$, $\rho$ 与典则的包含同态 ${\pi }_1(U_i,x_0)\hookrightarrow {\pi }_1(U_1,x_0)\ast {\pi }_1(U_2,x_0)$ 的复合与 $j_{i\ast }$ 相等. Seifert–van Kampen 定理的第一部分断言 $\rho$ 是满同态.

由于 $j_{1\ast }\circ {\iota }_{1\ast }=j_{2\ast }\circ {\iota }_{2\ast }$, 对任何 $\gamma \in {\pi }_1(U_1\cap U_2,x_0)$, 我们有$$\rho ({\iota }_{1\ast }(\gamma ))=\rho ({\iota }_{2\ast }(\gamma )).$$换言之, 对任意 $\gamma \in {\pi }_1(U_1\cap U_2,x_0)$, ${\iota }_{1\ast }(\gamma )\cdot {\iota }_{2\ast }({\gamma }^{-1})\in \mathrm{K}\mathrm{e}\mathrm{r}(\rho )$. Seifert–van Kampen 定理的第二部分断言上述关系在自由积 ${\pi }_1(U_1,x_0)\ast {\pi }_2(U_2,x_0)$ 中生成的正规子群就是 $\mathrm{K}\mathrm{e}\mathrm{r}(\rho )$.

定理 10.1.1. 记号如上.

1.	自然同态$$\rho :{\pi }_1(U_1,x_0)\ast {\pi }_1(U_2,x_0)\to {\pi }_1(X,x_0)$$是满同态.
2.	我们有$$\mathrm{K}\mathrm{e}\mathrm{r}(\rho )=⟨⟨{\iota }_{1\ast }(\gamma )\cdot {\iota }_{2\ast }({\gamma }^{-1}):\gamma \in {\pi }_1(U_1\cap U_2,x_0)⟩⟩$$

结合两部分断言以及同态基本定理, 我们有$${\pi }_1(X,x_0)\cong \frac{{\pi }_1(U_1,x_0)\ast {\pi }_2(U_2,x_0)}{⟨⟨{\iota }_{1\ast }(\gamma )\cdot {\iota }_{2\ast }({\gamma }^{-1}):\gamma \in {\pi }_1(U_1\cap U_2,x_0)⟩⟩}.$$

系 10.1.2. 记号如上. 如果 $U_1\cap U_2$ 道路单连通, 则 ${\pi }_1(X,x_0)\cong {\pi }_1(U_1,x_0)\ast {\pi }_1(U_2,x_0)$.

由于我们关心的大多数空间 (流形, 胞腔空间) 具有良好的 “局部” 性质, 我们将在下一章对这些 “好” 空间证明定理 10.1.1.

我们可以利用泛性质重新陈述 Seifert–van Kampen 定理. 如果对某个群 $G^{\prime }$, 我们有下面的交换图那么上一段的讨论表明:

$\diamond$	存在自然同态 ${\rho }^{\prime }:{\pi }_1(U_1,x_0)\ast {\pi }_1(U_2,x_0)\to G^{\prime }$,
$\diamond$	正规子群 $⟨⟨{\iota }_{1\ast }(\gamma )\cdot {\iota }_{2\ast }({\gamma }^{-1}):\gamma \in {\pi }_1(U_1\cap U_2,x_0)⟩⟩$ 包含于 $\mathrm{K}\mathrm{e}\mathrm{r}({\rho }^{\prime })$ 中.

根据同态基本定理, 存在唯一同态$$u:{\pi }_1(X,x_0)\cong \frac{{\pi }_1(U_1,x_0)\ast {\pi }_1(U_2,x_0)}{⟨⟨{\iota }_{1\ast }(\gamma )\cdot {\iota }_{2\ast }({\gamma }^{-1}):\gamma \in {\pi }_1(U_1\cap U_2,x_0)⟩⟩}\to G^{\prime }$$满足 $u\circ \rho ={\rho }^{\prime }$. 换言之, 给定下面的图表, 存在唯一的虚箭头使得整个图都交换:

这就是 Seifert–van Kampen 利用泛性质的重述. 将上述泛性质提炼出来, 我们得到了群映射的推出 (pushout) 的概念.

定义 10.1.3. 令 $a_1:H\to G_1$, $a_2:H\to G_2$ 为群同态. 则 $G_i$ 沿着 $a_i$ 的推出, 记为 $G_1{\ast }_H{G}_2$, 是三元组 $(G,b_1:G_1\to G,b_2:G_2\to G)$, 其中 $G$ 是群, $b_i$ 是群同态. 它们满足: $b_1\circ a_1=b_2\circ a_2$, 以及下述泛性质.

(PO)	若同态 ${\varphi }_1:G_1\to G^{\prime }$ ${\varphi }_2:G_2\to G^{\prime }$ 满足 ${\varphi }_1\circ a_1={\varphi }_2\circ a_2$, 则存在唯一同态 $\varphi :G\to G^{\prime }$, 使得 ${\varphi }_i=\varphi \circ b_i$.

换言之, 下面的图表可以被唯一的虚箭头变成交换图: 无歧义时, 我们也用 $G_1{\ast }_H{G}_2$ 代表推出中的群 $G$.

定理 10.1.4 (Seifert–van Kampen 利用泛性质的重述). 记号如前, 我们有$${\pi }_1(X,x_0)\cong {\pi }_1(U_1,x_0){\ast }_{{\pi }_1(U_1\cap U_2,x_0)}{\pi }_1(U_2,x_0).$$

10.2Seifert–van Kampen 定理的简单应用

空间的一点并

考虑带基点的拓扑空间 $(X,x)$ 与 $(Y,y)$. 它们的一点并, 或楔和 (wedge sum) $(X,x)\vee (Y,y)$ 是商空间$$\frac{X⨿Y}{x\sim y}$$并以 $x$ 在其中的像为基点. 我们假设: $x$ 在 $X$ 中有一个开邻域 $U$, 且 $U$ 以 $x$ 为形变收缩核; $y$ 在 $Y$ 中有一个开邻域 $V$, 且 $V$ 以 $y$ 为形变收缩核. 在此条件下, 我们断言$${\pi }_1((X,x)\vee (Y,y))\cong {\pi }_1(X,x)\ast {\pi }_1(Y,y).$$事实上, $X\vee V$ 与 $U\vee Y$ 构成了 $X\vee Y$ 的一个开覆盖. 它们的交 $U\vee V$ 以 $x$ 的像为形变收缩核, 而这两个开集分别以 $X$ 和 $Y$ 为形变收缩核. 这些观察与系理 10.1.2 便推出了上述断言. 特别地, 若干个圆周的一点并的基本群是自由群.

安装胞腔

令 $X$ 为道路连通拓扑空间. $\phi :{\mathbb{S}}^{n-1}\to X$ 为连续映射. 令 $Y=X{⨿}_{\phi }{D}^n$ 为向空间 $X$ 沿着 $\phi$ 安装 $n$ 维胞腔得到的空间. 我们来计算 $Y$ 的基本群.

$\diamond$	如果 $n=1$, 我们有 ${\pi }_1(Y)\cong {\pi }_1(X)\ast \mathbb{Z}$ (证明留给读者, 比如这个结论可以用下一节中的 “闭版本” 的 van Kampen 定理推出).
$\diamond$	如果 $n=2$, 则 $Y$ 可以写成两个空间的并: $$Y=U\cup V,$$其中 $U$ 同胚于 $\phi$ 的映射柱, 而 $V$ 同胚于 $D^2$, $U\cap V$ 以 ${\mathbb{S}}^1$ 为形变收缩核. 应用定理 10.1.1, 我们得到$${\pi }_1(Y)\cong {\pi }_1(X)/⟨⟨{\phi }_{\ast }(\gamma )⟩⟩$$其中 $\gamma$ 是 ${\mathbb{S}}^1$ 的基本群的一个生成元.
$\diamond$	如果 $n\ge 3$, 重复上面的论证, 但使用 ${\mathbb{S}}^{n-1}$ 的道路单连通性, 我们就得到 ${\pi }_1(Y)\cong {\pi }_1(X)$.

我们用这个方法来 (再度) 计算实射影空间 $\mathbb{R}{\mathrm{P}}^n$ 的基本群. 由于对 $n\ge 3$, $\mathbb{R}{\mathrm{P}}^n$ 是累次向 $\mathbb{R}{\mathrm{P}}^2$ 安装高维胞腔得到的, 我们有 ${\pi }_1(\mathbb{R}{\mathrm{P}}^n)\cong {\pi }_1(\mathbb{R}{\mathrm{P}}^2)$. 而 $\mathbb{R}{\mathrm{P}}^2$ 是向 ${\mathbb{S}}^1$ 用 $z\mapsto z^2$ 安装二维胞腔得到的, 我们有$${\pi }_1(\mathbb{R}{\mathrm{P}}^2)\cong \mathbb{Z}/(2).$$

10.3闭版本的 van Kampen 定理

许多人 (谁) 嘲笑上述 Seifert–van Kampen 定理不足以计算圆周的基本群. 然而定理 10.1.1 只是从 van Kampen 的论文中撷取的一部分. 他的文章中还包含了所谓的 “闭的 van Kampen 定理” (以及更一般的论述). 这个版本的 van Kampen 定理可以用来计算圆周的基本群. 为了陈述它, 我们设计一下记号.

令 $A_1$ 与 $A_2$ 为道路连通拓扑空间 $X$ 的互不相交的道路连通闭子空间. 令 ${\iota }_1:A_1\to X$, ${\iota }_2:A_2\to X$ 为包含映射. 设存在包含 $A_i$ 的开集 $U_i$, 满足:

$\diamond$	$A_i$ 是 $U_i$ 的形变收缩核,
$\diamond$	$U_1\cap U_2=\varnothing$.

给定同胚 $\phi :A_1\to A_2$, 令$$Y=\frac{X}{[a\sim \phi (a),\forall a\in A_1]}$$为用 $\phi$ 粘合 $A_1,A_2$ 得到的拓扑空间.

令 $p:X\to Y$ 为商映射. 对 $a\in A_1$, 令 $u$ 为一条从 $a$ 到 $\phi (a)$ 的道路. 对 $\gamma \in {\pi }_1(A_1,a)$, 我们仍然用 $\gamma$ 来表示它在 ${\pi }_1(X,a)$, 中的像, 用 ${\gamma }^{\phi }$ 来表示回路 $u\cdot {\iota }_2{\phi }_{\ast }(\gamma )\cdot u^{-1}\in {\pi }_1(X,a)$.

定理 10.3.1. 记号如上. 我们有$${\pi }_1(Y,p(a))\cong \frac{{\pi }_1(X,a)\ast t^{\mathbb{Z}}}{N}$$($t^{\mathbb{Z}}$ 代表由 $t$ 生成的自由群), 其中 $N$ 是由一切$$t\cdot {\gamma }^{\phi }\cdot t^{-1}\cdot {\gamma }^{-1}(\gamma \in {\pi }_1(A_1,a)),$$生成的正规子群.

我们仍然只对有良好局部性质的空间证明定理 10.3.1.

下面是定理 10.3.1 的两个简单应用

1.

${\mathbb{S}}^1=[0,1]/(0\sim 1)$. 由于 $\{0\},\{1\},[0,1]$ 的基本群都是平凡的, 我们有 ${\pi }_1({\mathbb{S}}^1,o)\cong t^{\mathbb{Z}}$ 是一个文字的自由群.

2.

考虑 Klein 瓶 $U$. 它是将柱面 ${\mathbb{S}}^1\times [0,1]$ 的两个子空间 $A={\mathbb{S}}^1\times \{0\}$ 和 $B={\mathbb{S}}^1\times \{1\}$ 用恒等映射粘贴起来的. 如果 $\gamma$ 是 ${\mathbb{S}}^1$ 的基本群的生成元, 那么在 ${\mathbb{S}}^1\times [0,1]$ 中, $c:={\iota }_{A\ast }\gamma ={\iota }_{B\ast }{\gamma }^{-1}$. 因此, $${\pi }_1(U,o)\cong \frac{c^{\mathbb{Z}}\ast t^{\mathbb{Z}}}{⟨⟨t{c}^{-1}{t}^{-1}{c}^{-1}⟩⟩}$$于是 ${\pi }_1(U,o{)}^{\mathrm{a}\mathrm{b}}\cong \mathbb{Z}\oplus \mathbb{Z}/(2)$.

10.4闭曲面的基本群

闭曲面是指紧连通二维流形. 球面 ${\mathbb{S}}^2$, 环面 ${\mathbb{S}}^1\times {\mathbb{S}}^1$, 射影平面 $\mathbb{R}{\mathrm{P}}^2$, 和上面说的 Klein 瓶都是闭曲面. 它们的基本群分别是$$\{1\},\mathbb{Z}\oplus \mathbb{Z},\mathbb{Z}/(2),\frac{c^{\mathbb{Z}}\ast t^{\mathbb{Z}}}{⟨⟨t{c}^{-1}{t}^{-1}{c}^{-1}⟩⟩}$$在接下来的段落里, 我们引入一些新的曲面的例子, 并且来计算它们的基本群.

安装环柄

令 $S$ 为闭曲面. $S$ 上的一个小碟子是一个 $S$ 的闭子空间, 它是某个 $S$ 同胚于 ${\mathbb{R}}^2$ 的开集里由$$\{(x,y)\in {\mathbb{R}}^2:x^2+y^2\le 1\}.$$定义的子空间的逆像.

向 $S$ 安装环柄是这样的操作: 先挑两个互不相交的小碟子 $B_0$, $B_1$, 令 $C_0$, $C_1$ 是它们的边界圆周, 定义$$S^{\prime }=(S\setminus (B_0^{\circ }\cup B_1^{\circ })){⨿}_{C_1⨿C_2}{S}^1\times [0,1]$$其中 $S^1\times \{0\}$ 被等同于 $C_0$, $S^1\times \{1\}$ 被等同于 $C_1$. 下图是安装了两个环柄的球面的示意图 (从 Zeeman 的讲义中偷窃而来):

留给读者验证安装环柄了之后得到的拓扑空间仍然是闭曲面.

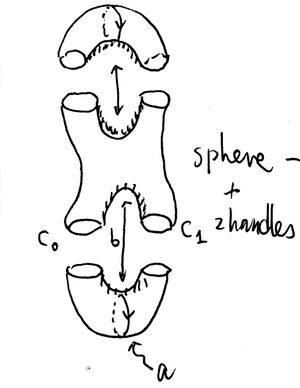
命题 10.4.1. 令 ${\mathbb{T}}_g$ 为向 ${\mathbb{S}}^2$ 安装了 $g$ 个不同环柄得到的空间. 则 ${\mathbb{T}}_g$ 的基本群有如下表现: $${\pi }_1({\mathbb{T}}_g)=⟨a_1,\dots ,a_g,b_1,\dots ,b_g\mid [a_1,b_1][a_2,b_2]\cdots [a_g,b_g]⟩.$$其中, $a_i$ 是绕着第 $i$ 个管子的圆周给出的道路同伦类, $b_i$ 是穿越了第 $i$ 个管子表面的道路同伦类, 如下图所示.

这个命题通常是利用通过曲面的平面模型和利用 “安装胞腔” 一节的结论予以证明. 我们则故意选择使用闭版本的 van Kampen 来证.

证明的梗概. 不难看出 ${\mathbb{T}}_g$ 可以如下得到: 先从球面上移走 $2g$ 个小碟子的内部, 得到 “带边” 曲面 $S_0$, 然后用同伦于 $-\mathrm{I}\mathrm{d}$ 的映射粘贴 $C_0^{(i)}$, $C_1^{(i)}$ (思考: 为什么定向被搞反了?).

则 $S_0$ 具有 $2g-1$ 个 ${\mathbb{S}}^1$ 的一点并同伦型, 并且它的基本群有如下表现: $${\pi }_1(S_0)\cong ⟨a_0^{(1)},a_1^{(1)},\dots ,a_0^{(g)},a_1^{(g)}\mid a_0^{(1)}{a}_1^{(1)}\cdots a_0^{(g)}{a}_1^{(g)}⟩.$$这里 $a_j^{(i)}$ 是绕着圆周 $C_j^{(i)}$ 按照诱导定向走一圈决定的回路. 从 $S_0$ 到 ${\mathbb{T}}_g$, 我们可以把粘合一下子全搞定, 也可以一步步来: 先用 ${\phi }_1$ 粘合 $C_0^{(1)}$, $C_1^{(1)}$, 再用 ${\phi }_2$ 粘合 $C_0^{(2)}$, $C_1^{(2)}$, 等等. 中间第 $m$ 步得到的曲面记作 $S_m$.

由于粘合映射 ${\phi }_1$ 反定向, 我们有 $(a_0^{(1)}{)}^{{\phi }_1}=(a_1^{(1)}{)}^{-1}$. 闭版本的 van Kampen 推出$${\pi }_1(S_1)=\frac{{\pi }_1(S_0)\ast b_1^{\mathbb{Z}}}{⟨⟨b_1(a_1^{(1)}{)}^{-1}{b}_1^{-1}(a_0^{(1)}{)}^{-1}⟩⟩}$$于是变量 $b_1,a_1:=a_1^{(1)}$ 可以用来代表 $a_0^{(1)}$. 在表现里我们可以把 $a_0^{(1)}$ 消去, 从而得到新的表现: $${\pi }_1(S_1)=⟨a_1,b_1,a_0^{(2)},a_1^{(2)},\dots \mid [a_1,b_1]\cdot a_0^{(2)}{a}_1^{(2)}\cdots ⟩.$$继续搞下去, 读者应该就能够发现一般规律并且结束证明了.

$■$

系 10.4.2. 对于闭曲面 ${\mathbb{T}}_g$, 有$$\frac{{\pi }_1({\mathbb{T}}_g)}{[{\pi }_1({\mathbb{T}}_g),{\pi }_1({\mathbb{T}}_g)]}\cong {\mathbb{Z}}^{2g}.$$

因此它们两两不同胚.

安装错帽

设 $S$ 是闭曲面, 则向 $S$ 安装一个错帽 (cross-cap) 是如下操作. 选择 $S$ 上小碟子 $B$. 将 $B$ 内部拿掉, 并沿着它的边界圆周 $C$ 以及 Möbius 带的外圈圆周粘贴上 Möbius 带 $M$:$$(S\setminus B^{\circ }){⨿}_{C}M.$$

命题 10.4.3. 令 ${\mathbb{U}}_h$ 是向 ${\mathbb{S}}^2$ 安装了 $h$ 个不同错帽得到的空间. 则 ${\pi }_1({\mathbb{U}}_h)$ 有如下表现: $${\pi }_1({\mathbb{U}}_h)=⟨b_1,\dots ,b_h\mid b_1^2\cdots b_h^2⟩$$

证明概要. 首先将 ${\mathbb{S}}^2$ 挖去 $h$ 个小碟子, 得到带边流形 $S_0$. $S_0$ 的基本群具有表现$$⟨a_1,\dots ,a_h\mid a_1\cdots a_h⟩,$$其中 $a_i$ 是碟子边界的圆周 $C_i$ 的按诱导定向跑的回路. 先安装第一个错帽, 得到带边曲面 $S_1$. 此时根据标准的 van Kampen 定理, 有$$S_1=\frac{{\pi }_1(S_0)\ast b_1^{\mathbb{Z}}}{⟨⟨a_1{b}_1^{-2}⟩⟩}.$$因此 $S_1$ 的基本群具有表现$$⟨b_1,a_2,\dots ,a_h\mid b_1^2{a}_2\cdots a_h⟩.$$继续安装错帽就得到了所需的结果.

$■$

系 10.4.4. 我们有$$\frac{{\pi }_1({\mathbb{U}}_h)}{[{\pi }_1({\mathbb{U}}_h),{\pi }_1({\mathbb{U}}_h)]}\cong \mathbb{Z}/(2)\oplus {\mathbb{Z}}^{h-1}.$$

特别地, ${\mathbb{U}}_h$, ${\mathbb{T}}_g$ 两两不同胚.

今后我们将会证明, 任何闭曲面要么同胚于 ${\mathbb{T}}_g$, 要么同胚于 ${\mathbb{U}}_h$.

10.5习题

10.5.1. 利用闭版本的 van Kampen 定理计算 Poincaré 第六个例子的基本群. (我们在课上用了覆盖空间的方法.) 令 ${\mathbb{T}}^2={\mathbb{R}}^2/{\mathbb{Z}}^2$ 为环面. 定义$$V_A=\frac{{\mathbb{T}}^2\times [0,1]}{(x,0)\sim (f_A(x),1)}.$$其中 $f_A:{\mathbb{T}}^2\to {\mathbb{T}}^2$ 是线性映射$$A=\left[\begin{array}{cc}\alpha & \beta \\ \gamma & \delta \end{array}\right]\in {\mathrm{S}\mathrm{L}}_2(\mathbb{Z})=\{A\in {\mathrm{M}}_2(\mathbb{Z}):\det A=1\}$$诱导的 ${\mathbb{T}}^2$ 的同胚: $$f_A([(x,y{)}^T])=[A\cdot (x,y{)}^T].\text{\hspace{1em}(∗)}$$(10.1)

1.	证明 $V_A$ 的基本群有如下表现: $$⟨t_1,t_2,g_A|\begin{array}{c}{t}_1{t}_2=t_2{t}_1,\\ g_A{t}_1{g}_A^{-1}=t_1^{\alpha }{t}_2^{\gamma },\\ g_A{t}_2{g}_A^{-1}=t_1^{\beta }{t}_2^{\delta }\end{array}⟩.$$
2.	计算 ${\pi }_1(V_A)$ 的 Abel 化. 找出两个矩阵 $A$, $A^{\prime }$, 说明 $V_A$ 不同胚于 $V_{A^{\prime }}$.

10.5.2 (Heegaard 分解的基本群). 考虑一个 “亏格” 为 $g$ (下图的 $g=2$) 的实心三维环柄 $\Sigma$. 这是一个 ${\mathbb{R}}^3$ 中的带边流形, 它的 “边界” $\partial \Sigma$ 是一个 “亏格” 为 $g$ 的 ${\mathbb{R}}^3$ 中的曲面.

1.	证明 $\Sigma$ 的基本群是 $g$ 个文字的自由群.
2.	如果 ${\Sigma }^{\prime }$ 是另一个三维环柄. 设 $\phi :\partial \Sigma \to \partial {\Sigma }^{\prime }$ 为一个同胚. 用 Seifert–van Kampen 定理解释如何计算 $V=\Sigma {⨿}_{\partial \Sigma ,\phi }{\Sigma }^{\prime }$ 的基本群.
3.	假设 $\Sigma$ 的亏格为 $1$, $\phi$ 是由 ${\mathrm{S}\mathrm{L}}_2(\mathbb{Z})$ 中元素$$\left[\begin{array}{cc}\alpha & \beta \\ \gamma & \delta \end{array}\right]$$决定的环面之间的 “线性映射”. 证明 $V$ 的基本群同构于 $\mathbb{Z}/(\gamma )$.

事实上, 任何紧三维流形都可以通过第二款的方式得到. 将三维流形拆成环柄后, 沿着边界曲面粘贴的方法叫做三维流形的 Heegaard 分解. 上述习题第三款描述了透镜空间的 Heegaard 分解.

10.5.3. 令 $f(z_0,z_1,\dots ,z_n)={\sum }_{i=1}^n{z}_i^2$.

1.	如果 $n\ge 2$, 证明 $Y=\{(z_0,\dots ,z_n)\in {\mathbb{C}}^{n+1}:f(z)=1\}$ 是道路单连通空间.
2.	证明对任何 $n\ge 2$, $H_n=\{[z_0,\dots ,z_n]\in \mathbb{C}{\mathrm{P}}^n:f(z)=0\}$ 是道路单连通空间.
3.	如果 $n\ge 2$, 证明俨开集 $U_f=\{[z_0,\dots ,z_n]\in \mathbb{C}{\mathrm{P}}^n:f(z)\ne 0\}$ 的基本群是 $\mathbb{Z}/(2)$.
4.	求 ${\mathbb{C}}^{n+1}\setminus \{z\in {\mathbb{C}}^{n+1}:f(z)=0\}$ 的基本群.

10.5.4 (Brieskorn 流形 ¹). 令 $X=\{(z_0,z_1,z_2,z_3)\in {\mathbb{C}}^4:z_0^3=z_1^2+z_2^2+z_3^2\}$. 令 $\Sigma =X\cap {\mathbb{S}}^7\subset {\mathbb{C}}^4$. 在这个习题中, 我们来证明 $\Sigma$ 为道路单连通空间.

1.	考虑群 ${\mathbb{R}}_{>0}$ 在 $X\setminus \{0\}$ 上的作用$$(r,z)\mapsto (r^{\frac{1}{3}}{z}_0,r^{\frac{1}{2}}{z}_1,r^{\frac{1}{2}}{z}_2,r^{\frac{1}{2}}{z}_3).$$证明 ${\mathbb{S}}^5$ 与任何等价类都只有一个交点. 由此说明 $\Sigma \cong X/{\mathbb{R}}_{>0}$.
2.	考虑映射$$\pi :X\setminus \{0\}\to {\mathbb{C}}^3\setminus \{0\},z\mapsto (z_1,z_2,z_3).$$证明在集合 $Y=\{z\in {\mathbb{C}}^3:z_1^2+z_2^2+z_3^2=0\}$ 之外, $\pi$ 是覆盖映射. 由于 $\pi$ 尊重显然的 ${\mathbb{C}}^3\setminus \{0\}$ 上的 ${\mathbb{R}}_{>0}$ 作用, 它诱导了商空间之间的连续映射$$p:\Sigma \to {\mathbb{S}}^5.$$
3.	令 $D={\mathbb{S}}^5\cap Y$. 证明 $p$ 诱导了覆盖映射 $\Sigma \setminus p^{-1}(D)\to {\mathbb{S}}^5\setminus D$. 通过这个映射计算 $\Sigma \setminus p^{-1}(D)$ 的基本群.
4.	描述 $D$ 在 ${\mathbb{S}}^5$ 中的开邻域. 用 Seifert–van Kampen 定理来计算 $\Sigma$ 的基本群.

由 S. Smale 所证明的广义 Poincaré 猜想断言, 任何维数 $\ge 5$ 的道路单连通 “同调球面” 都同胚于球面. 使用基本的同调的计算手段可以证明 $\Sigma$ 是同调球面. 因此 $\Sigma$ 同胚于 ${\mathbb{S}}^5$. 另一方面, $\{z\in {\mathbb{C}}^3:z_0^3=z_1^2+z_2^2+z_3^2,|z|\le 1\}$ 同胚于 $\Sigma$ 的锥, 故同胚于 $D^6$. 因此, 尽管原点是超曲面 $X$ 的 “复解析奇异点”, $X$ 作为拓扑空间仍然是六维流形. 与此相反的现象是 D. Mumford 关于复曲面的定理: 一个 “正规” 的复曲面 (实四维) 在它的复解析奇异点附近不是流形 ².

类似的计算也可以用来处理多项式 $z_0^3={\sum }_{i=1}^n{z}_i^2$ 所定义出来的空间 $X$. 当 $n=5$ 时, $X\cap {\mathbb{S}}^{11}$ 同胚于 ${\mathbb{S}}^9$, 但是它的自然微分结构不同于 ${\mathbb{S}}^9$ 的标准微分结构 (“Kervaire 9 维怪球”). 建议读者参考 F. Hirzebruch 的 Bourbaki 报告 “Singularities and exotic spheres”.

在对大量例子进行细致分析后, J. Milnor 在他的书 “Singular points of complex hypersurfaces” 中证明了更一般的定理: 复维数 $\ge 3$ 的 “超曲面奇异点” 的链环都是单连通的

1.	Brieskorn, Egbert V. (1966), “Examples of singular normal complex spaces which are topological manifolds”, Proceedings of the National Academy of Sciences, 55 (6): 1395–1397.
2.	The topology of normal singularities of an algebraic surface and a criterion for simplicity, Inst. Hautes Études Sci. Publ. Math. No. 9 (1961), 5–22.

10.5.5. 令 $F$ 为拓扑空间. ${\mathbb{S}}_{+}^n$, ${\mathbb{S}}_{-}^n$ 分别是 ${\mathbb{S}}^n$ 去掉南北极后得到的空间. 一个 ${\mathbb{S}}^n$ 上具有纤维型 $F$ 的纤维空间是一个 ${\mathbb{S}}^n$ 上的空间 $(E,p)$, 且存在同胚 ${\phi }_{\pm }:p^{-1}{\mathbb{S}}_{\pm }^n\cong {\mathbb{S}}_{\pm }^n\times F$ 满足 $p{|}_{p^{-1}{\mathbb{S}}_{\pm }^n}={\mathrm{p}\mathrm{r}}_1\circ {\phi }_{\pm }$. 令 $E_{\pm }=p^{-1}({\mathbb{S}}_{\pm }^n)$.

1.	假设 $F$ 道路连通. 若 $n\ge 3$, 计算 ${\pi }_1(E)$. 若 $n=2$, 情况如何?
2.	令 $\mathrm{S}\mathrm{O}(n)$ 为特殊正交群. 设 $n\ge 2$, 证明 $p:\mathrm{S}\mathrm{O}(n)\to {\mathbb{S}}^{n-1}$, $p(A)=A$ 的第一列将 $\mathrm{S}\mathrm{O}(n)$ 实现为 ${\mathbb{S}}^{n-1}$ 上的纤维空间. 它的纤维型是什么? 据此, 计算 $\mathrm{S}\mathrm{O}(n)$ 的基本群.
3.	考虑上一问 $n=3$ 的情况. 我们给出 Poincaré 髪球定理的又一证明. 假设 ${\mathbb{S}}^2$ 存在处处不为零的切向量场. 证明 $\mathrm{S}\mathrm{O}(3)\to {\mathbb{S}}^2$ 存在截面, 并由此导出 ${\mathbb{S}}^2\times \mathrm{S}\mathrm{O}(2)$ 同胚于 $\mathrm{S}\mathrm{O}(3)$. 这与 $\mathrm{S}\mathrm{O}(3)$ 基本群为 $\mathbb{Z}/(2)$ 矛盾.