作业: 波动方程的局部能量估计
课堂补充
A1) | (闭子空间) 是 Hilbert 空间, 是其线性子空间. 我们假设 是 中的闭集 (相对于 上由内积所定义的距离函数而言) . 证明, 对任意的 , 如果我们仍用 作为 上的内积, 那么 是 Hilbert 空间. 证明, 对于 , 不是闭子空间. |
A2) | 给定 中的函数序列 , 我们假设它们在 范数下收敛到 , 即那么, 存在子函数序列 , 使得对几乎处处的 , 我们都有 |
A3) | 证明, 中没有单位元, 即不存在 , 使得对任意的 , 都有 . |
A4) | 证明, 是 的稠密子空间. |
A5) | 举例说明 不是稠密的. |
A6) | 证明, 在 中稠密 (对 而言) . |
A7) | 假设 是 Hilbert 空间, 是线性子空间. 证明, 在 中稠密当且仅当对任意的 一定有 . |
A8) | 试证明, 是可分的. (可以参考讲义中的提示) |
A9) | (重要) 假设 并且 , 我们定义证明, 对任意的有紧支集的连续函数 , 我们都有如下的一致收敛: |
控制收敛与 Fubini 定理的复习
含参数积分的研究
B1) | 证明, 对任意的 , 如下积分是良好定义的: |
B2) | 证明, 是 的连续函数. |
B3) | 证明, 是可导的. |
B4) | 试计算 . |
B5) | 证明, 对 , 如下的积分是发散的: |
B6) | 证明, 对任意的 , 如下在 Riemann 意义下的反常积分是良好定义的: 即 存在. |
B7) | 证明, 是 的连续函数. |
B8) | 试计算 . |
Laplace 变换的基本性质
C1) | 假设 是 上定义的 Lebesgue 可积函数. 我们定义它的 Laplace 变换为: 其中 . 证明, 是 的函数. |
C2) | 证明, 对任意的 , 我们都有 |
C3) | 假设 和 是 上定义的 Lebesgue 可积函数, 我们定义它们的 “卷积” 为证明, . |
C4) | 假设 和 是 上定义的 Lebesgue 可积函数. 证明, |
Stokes 公式的应用: 波动方程的局部能量估计
假设 是 上的光滑函数, 这里空间变量 , 时间变量 . 我们假设 满足波动方程: 其中波动算子的定义如下: 我们令 , , 这样的一对函数 被称作是波动方程的初始值.
我们做如下的假设: 对任意的时间 , 对 而言有紧支集.
D1) | 我们定义波动方程的能量函数证明能量守恒定律: 对任意的时刻 , 有 | ||||||||
D2) | 对于 , 我们定义波动方程的动量函数证明动量守恒定律: 对任意的时间 , 有 | ||||||||
D3) | (解的唯一性) 假设 和 都满足波动方程以及上面的假设. 证明, 如果它们具有相同的初始值, 即 , , 那么 . | ||||||||
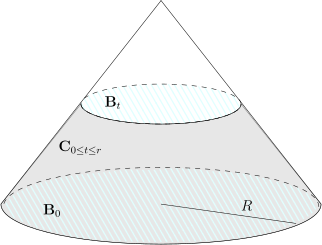
D4) | 任意给定 , 假设 . 我们在时空 中定义如下的几何对象:
给定 . 证明, 在这一点处的切空间由以下三个向量张成 (球坐标系) 作为传统的记号, 我们记 . | ||||||||
D5)** | 我们定义局部能量证明, 对任意的 , 我们都有(提示: 对 两边同时乘以 并在区域 上积分, 你需要运用 Stokes 公式来得到边界上的积分) | ||||||||
D6)* | (波方程的有限传播速度) 我们现在只假设 是光滑的. 证明, 如果 和 有紧支集, 那么对任意的时刻 , 对 有紧支集. | ||||||||
D7)* | 假设 是光滑函数并且满足非线性波动方程证明, 如果 和 有紧支集, 那么对任意的时刻 , 对 有紧支集. |
寄语. In order to solve this differential equation you look at it until a solution occurs to you.
—— George Pólya