作业: 高木贞治函数
基本习题
习题 A: 导数的定义和计算
A1) | 上配有范数 , 我们考虑映射证明, 在 处的导数存在当且仅当对每个分量函数 , 它在 处的导数都存在并且 |
A2) | 考虑函数 , 将它视作是映射利用定义证明, . 仿照课堂上的做法证明 . |
A3) | 利用上面两个问题的结论计算 和 的导数. |
A4) | 对 来验证 Faà di Bruno 公式. |
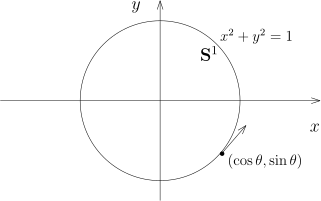
A5) | 定义映射我们用下面符号表示平面上的单位圆: 证明, 上的点可以写成 的形式, 即 . 试计算 并验证对于这个映射 ( 上取值) , Rolle 中值定理并不成立. |
A6) | 求下列函数的导数 (如果 在 不可微, 但单侧左导数或右导数存在时, 求出左导数或右导数) |
A7) | 求下列函数的 -阶导数: |
A8) | 如果函数 在点 处的导数 , 不能推出存在该点的领域 , 使得 在这个邻域上是递增的: 考虑函数 证明, 在 处导数存在且大于零, 但是对任意的 , 在 上的限制都不是单调函数. |
A9) | (重要) 是 的单位矩阵, , 计算 , 即 在 处的导数. |
A10) | 证明, (可微的) 奇函数的导数是偶函数, (可微的) 偶函数的导数是奇函数. |
A11) | 证明, Riemann 函数 在 上处处不可微. |
习题 B
B1) | 定义双曲函数:
| ||||||||||||||
B2) | 设 , , 考察函数 , 其中证明, 下述关于 的结论都成立:
|
习题 C: 无穷小量与无穷大量的阶的比较
如果函数 在 的附近 (即某个 的开邻域去掉 ) 满足 , 我们就称 是 时的无穷小量; 类似地, 如果 或者 (其注意我们用的 “或者” 这个词的含义) , 我们就称 是 时的无穷大量.
现在假设 都是 时的无穷小量并且 在 的附近不取零值, 我们现在引进记号:
• | 如果 , 我们就称 是比 高阶的无穷小, 记作 ; |
• | 如果 , 我们就称 是与 同阶的无穷小; |
• | 特别地, 如果 与 同阶并且 , 我们就称 是与 等价的无穷小, 记作 ; |
• | 如果 , 我们将这种情况记作 . |
类似地, 我们可以定义无穷大量的阶之间的比较. 这是通用的术语, 同学们可参考任一本参考书或者网络.
C1) | 假设 时, 函数 满足 . 试证明: | ||||||
C2) | 假设 是 时的无穷小, 那么
|
习题 T (思考题, 不交作业): 处处连续处处不可微的 Takagi(高木贞治) 函数, 1903
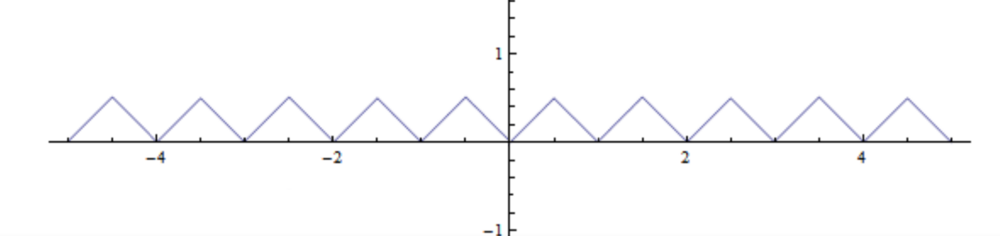
我们先在 区间上定义 接下来, 以 为周期, 我们可以将 延拓成 上的周期函数 (连续) 并且仍然将它记作 , 它的函数图像好像是锯齿一般:
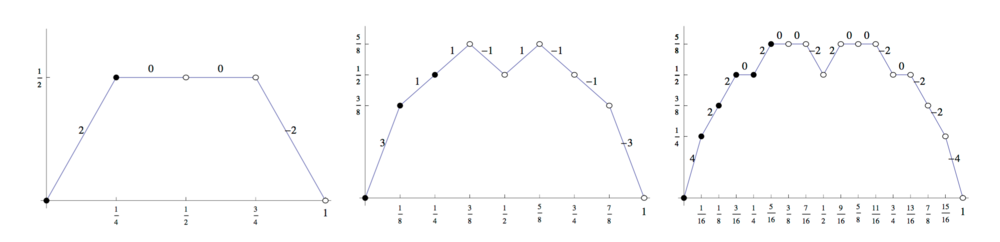
我们定义 Takagi 函数 如下: 我们实际上可以考虑部分和 . 当 时, 它们的图像如下:
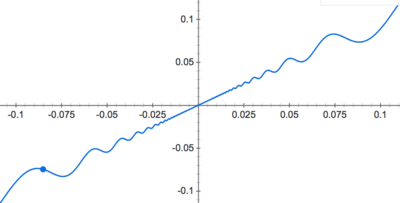
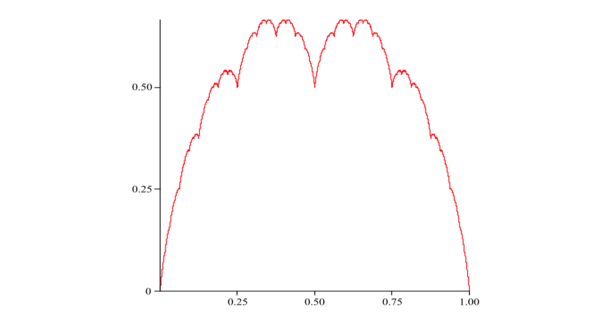
当 越来越大的时候, 它们的图像看起来逐渐地收敛:
这个习题的目标是粗略地研究 Takagi 函数的性质.
T1) | 证明, 是 上良好定义的有界连续函数. 它图像貌似: |
T2) | 对于 , 假设 是 的 -进制展开, 其中 或者 . 我们令 . 我们定义函数 , 其中 或者 . 证明, |
T3) | 对于 , 假设 是 的 -进制展开. 证明, |
T4) | 假设 , 其中 是奇数, . 令 , 其中 . 证明, 数列 不收敛. |
T5) | 是定义在非空的开区间 上实数值函数. 如果 在 处可导, 证明, 这里极限 的意义指的是任意的序列 所对应的序列都收敛. |
T6) | 是定义在非空的开区间 上实数值函数. 假设 (连续可微) , , 证明, |
T7) | 假设 , 使得对任意的正整数 , 都不是整数. 对于每个正整数 , 我们用下面的公式定义序列 和 : 其中函数 按照定义是不超过 的最大的整数 (即 的整数部分 (如果 ) ) . 证明, 对每个给定的 , 并且对每个整数 , 开区间 中不包含任何的整数和半整数. |
T8) | 假设 , 使得对任意的正整数 , 都不是整数, 我们沿用 E7) 中的符号, 证明, 数列 不收敛. |
T9) | 证明, 是 上处处连续处处不可微的函数. |
T10) | 证明, 我们有如下的函数方程: |
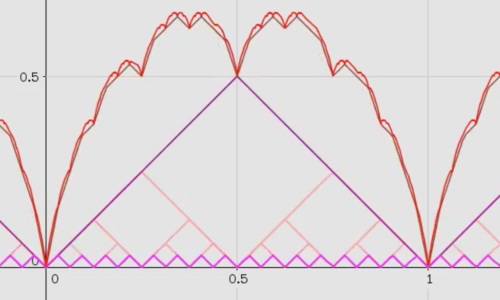
T11) | (Takagi 函数图像的自相似性) 令 是 在区间 上的函数图像. 我们定义如下四个仿射变换 : 证明, 恰好把 变成 在区间 上的图像, 其中 . |
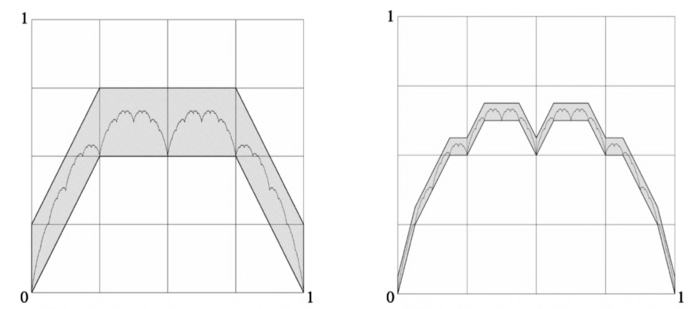
T12) | 令 是 上的闭方块. 对每个 , 我们定义 . 证明, 是平面上一列单调下降的紧集并且 . 我们有 和 的示意图: |
T13) | 证明, . |
T14) | 找一个 , 使得 . |
T15) | ( 的 Cantor 集的结构) 对于 , 假设 是 的 -进制展开, 其中 . 证明, |
T16) | 仿照 T11), 研究 和 在集合 上自相似的作用. (这是一个 Hausdorff 维数为 的集合) . |