15. 中值定理的应用

$x\mapsto \exp (xA)$ 的导数

按照导数的定义, 如果 $(V,\Vert \cdot \Vert )$ 是赋范线性空间, $f:\mathbb{R}\to V$ 是映射, 我们可以定义导数$$f^{\prime }(x_0)=\underset{x\to x_0}{\lim }\frac{f(x)-f(x_0)}{x-x_0}.$$(如果极限存在的话) 特别地, $f^{\prime }(x_0)\in V$. 我们来研究我们最爱的例子: $\exp$. 令 $V={\mathbf{M}}_n(\mathbb{R})$ 为矩阵的空间 (复数系数的矩阵的证明是一致的) , $A$ 是一个给定的 $n\times n$ 的矩阵, 考察映射$$f:\mathbb{R}\to {\mathbf{M}}_n(\mathbb{R}),x\mapsto e^{xA}.$$我们计算 $f^{\prime }(x_0)$. 按定义, 我们有$$\begin{array}{r}\frac{f(x_0+h)-f(x_0)}{h}=\frac{e^{(x_0+h)A}-e^{x_{0}A}}{h}=e^{x_{0}A}\frac{e^{hA}-1}{h},\end{array}$$其中我们用到了矩阵 $x_{0}A$ 与 $hA$ 可交换. 由此可见 (在证明 $(e^x{)}^{\prime }=e^x$ 的时候也做了同样的事情) , 只要计算 $f^{\prime }(0)$ 即可. 利用定义, 我们有$$\begin{array}{r}\frac{e^{hA}-1}{h}=\sum _{k=1}^{\infty }\frac{1}{k!}{h}^{k-1}{A}^k=A+\sum _{k=1}^{\infty }\frac{1}{(k+1)!}{h}^k{A}^{k+1}.\end{array}$$根据矩阵乘法对于范数的关系 ($\Vert A\cdot B\Vert ⩽c\Vert A\Vert \Vert B\Vert$, 其中 $\Vert \cdot \Vert$ 是任意一个指定的范数) , 我们有$$\Vert \sum _{k=1}^{\infty }\frac{1}{(k+1)!}{h}^k{A}^{k+1}\Vert ⩽h\sum _{k=1}^{\infty }\frac{1}{(k+1)!}{c}^k\Vert A{\Vert }^{k+1}⩽\frac{h}{c}{e}^{c\Vert A\Vert }.$$从而, $f^{\prime }(0)=A$. 进一步, 我们知道$$f^{\prime }(x)=A{e}^{xA}=Af(x).$$

中值定理的应用

上一次最后提到了 Lagrange 中值定理的一个推论 ¹:

推论 15.1 (常微分方程解的存在唯一性-儿童版本). $f\in C([a,b])$ 并且 $f$ 在 $(a,b)$ 上可微, 如果 $f^{\prime }(x)\equiv 0$ 并且 $f(a)=c$, 那么 $f(x)\equiv c$. 换而言之, 如下的常微分方程$$\{\begin{array}{ll}& f^{\prime }(x)=0,\\ & f{|}_{x=a}=c,\end{array}$$存在唯一的解 $f(x)=c$.

证明. 用反证法: 如果存在某个 $x_1\in (a,b)$ 使得 $f(x_1)\ne c$, 那么, 在 $[a,x_1]$ 上使用 Lagrange 中值定理, 就有 $x_0\in (a,x_1)$, 使得$$f^{\prime }(x_0)=\frac{f(x_1)-c}{x_1-a}\ne 0.$$矛盾.

$\square$

这个推论实际上对于在赋范线性空间中取值的映射也成立:

命题 15.2. 给定映射 $f\in C([a,b];V)$, $f$ 在 $(a,b)$ 上可微. 如果 $f^{\prime }(x)\equiv 0$, $f(a)=c$, 那么对任意的 $x\in [a,b]$, $f(x)=c$.

我们满足于 $V={\mathbb{R}}^n$ 是有限维的情形, 此时, $f:\mathbb{R}\to {\mathbb{R}}^n$ 可以用分量 $(f_1(x),\cdots ,f_n(x))$ 表达并且$$f^{\prime }(x)=(f_1^{\prime }(x),\cdots ,f_n^{\prime }(x))=0\iff f_k^{\prime }(x)\equiv 0,\text{任意的}k=1,\cdots ,n.$$所以, 利用 $1$ 维的情况就可以得到结论.

如果 $V$ 是无限维的赋范线性空间, 比如说 $\left(C\right([0,1]),\Vert \cdot {\Vert }_{\infty })$, 我们一方面没有 Lagrange 中值定理, 所以不能用本来的证明; 一方面想把问题约化成 $1$ 维的情况的做法不是很容易推广 (我们的确能做到这一点) . 然而, 我们不打算在这个问题上继续深入 (除非我们想仔细的研究一下微分方程理论) , 有限维的情况对我们就足够用了.

作为应用, 我们仍然回到 $\exp$ 这个例子: 考虑可微映射 $f:\mathbb{R}\to {\mathbf{M}}_n(\mathbb{R})$, 假设它满足如下的微分方程$$\{\begin{array}{ll}& f^{\prime }(x)=A\cdot f(x),\\ & f{|}_{x=0}={\mathbf{I}}_n,\end{array}$$其中, ${\mathbf{I}}_n$ 为 $n\times n$ 的矩阵. 我们知道, $x\mapsto e^{xA}$ 是这个方程的一个解. 我们现在说明, 这是唯一的解. 实际上, 我们有$$e^{-xA}(f^{\prime }-Af)=0\Rightarrow e^{-xA}{f}^{\prime }+(e^{-xA}{)}^{\prime }f=0.$$如果我们有 Leibeniz 法则的话 (两个函数相乘之后求导数的法则) , 那么就有$$(e^{-xA}f{)}^{\prime }=0.$$这是把一个表达式写成全微分的技巧. 根据唯一性的命题, 我们知道 $e^{-xA}f(x)\equiv \mathbf{I}$, 所以我们就证明了 $f(x)=e^{xA}$ (因为 $e^A{e}^{-A}={\mathbf{I}}_n$) .

回到 Leibniz 法则的问题, 如果 $f$ 和 $g$ 是 $n\times n$ 矩阵中取值的函数, 我们有$$\begin{array}{rl}(f\cdot g{)}^{\prime }(x_0)& =\underset{h\to 0}{\lim }\frac{f(x_0+h)g(x_0+h)-f(x_0)g(x_0)}{h}\\ & =\underset{h\to 0}{\lim }\frac{f(x_0+h)(g(x_0+h)-g(x_0))}{h}+\underset{h\to 0}{\lim }\frac{(f(x_0+h)-f(x_0))g(x_0)}{h}\\ & =f(x_0)g^{\prime }(x_0)+f^{\prime }(x_0)g(x_0).\end{array}$$这个证明和最基本的函数版本的证明没有任何的区别.

利用 Lagrange 中值定理, 我们可以进一步联系单调性和导数:

推论 15.3. 假设实值函数 $f\in C^0([a,b])$ 并且 $f$ 在 $(a,b)$ 上可微. 那么, 下面的两条性质是等价的:

1)	$f^{\prime }(x)⩾0$.
2)	$f(x)$ 是递增的.

特别地, 如果对任意 $x$, $f^{\prime }(x)>0$, 那么函数是严格递增的 (反之不然) .

证明. 2) $\Rightarrow$ 1) 用导数的定义即可: 由于 $f(x)$ 递增, 所以 $f(x+h)-f(x)$ 与 $h$ 的符号是一致的, 从而$$\frac{f(x+h)-f(x)}{h}⩾0.$$令 $h\to 0$ 即可.

1) $\Rightarrow$ 2) 用反证法: 如若不然, 存在 $x_1<x_2$, 使得 $f(x_1)>f(x_2)$, 根据 Lagrange 中值定理, 存在 $x_0\in [x_1,x_2]$, 使得$$f^{\prime }(x_0)=\frac{f(x_2)-f(x_1)}{x_2-x_1}<0.$$矛盾.

如果 $f^{\prime }(x)>0$, 为了说明函数是严格递增的, 我们仍然用反证法: 如若不然, 存在 $x_1<x_2$, 使得 $f(x_1)⩾f(x_2)$, 根据 Lagrange 中值定理, 存在 $x_0\in [x_1,x_2]$, 使得$$f^{\prime }(x_0)=\frac{f(x_2)-f(x_1)}{x_2-x_1}⩽0.$$矛盾.

$\square$

我们现在证明导函数的介值定理.

推论 15.4 (Darboux). 假设 $f$ 在 $[a,b]$ 上可微, $f^{\prime }(a)<f^{\prime }(b)$. 那么, 对于任意的 $c\in (f^{\prime }(a),f^{\prime }(b))$, 都存在 $x_0\in (a,b)$, 使得 $f^{\prime }(x_0)=c$.

注记. 存在在 $[a,b]$ 上可微的函数 $f$, 它的导数不一定连续 (因此不能直接使用连续函数的介值定理) : $$f(x)=\{\begin{array}{ll}{x}^2\sin (\frac{1}{x}),& x\ne 0;\\ 0,& x=0\end{array}$$很明显, 我们有$$f^{\prime }(x)=\{\begin{array}{ll}2x\sin (\frac{1}{x})-\cos (\frac{1}{x}),& x\ne 0;\\ 0,& x=0\end{array}$$我们来说明 $f^{\prime }(x)$ 在 $0$ 处不连续. 实际上, 我们考虑两个点列 $\{x_n{\}}_{n⩾1}$ 和 $\{y_n{\}}_{n⩾1}$, 其中$$x_n=\frac{1}{2n\pi },y_n=\frac{1}{(2n+1)\pi }.$$我们有 $\underset{n\to \infty }{\lim }{x}_n=\underset{n\to \infty }{\lim }{y}_n=0$, 但是, $$\underset{n\to \infty }{\lim }{f}^{\prime }(x_n)=-1,\underset{n\to \infty }{\lim }{f}^{\prime }(y_n)=1.$$

证明. 通过把 $f$ 换为 $f(x)-cx$, 我们不妨假设 $c=0$, $f^{\prime }(a)<0<f^{\prime }(b)$. 在这种假设下, $f$ 连续但是不是单调的函数 (因为导数是改变符号的) , 根据介值定理, $f$ 不能是单射. 所以, 存在 $x_1,x_2\in [a,b]$, 使得 $f(x_1)=f(x_2)$, 那么, Rolle 中值定理就给出了 $c$ 的存在性.

$\square$

另一个版本的中值定理叫做 Cauchy 中值定理, 描述了两个不同函数之间关系:

命题 15.5 (Cauchy 中值定理). 假设有实值函数 $f,g\in C([a,b])$ 并且 $f$ 和 $g$ 均在 $(a,b)$ 上可微. 假设对任意的 $x\in (a,b)$, $g^{\prime }(x)\ne 0$. 那么, 存在 $x_0\in (a,b)$, 使得$$\frac{f^{\prime }(x_0)}{g^{\prime }(x_0)}=\frac{f(b)-f(a)}{g(b)-g(a)}.$$

我们注意到, 结合 Darboux 的定理, $g^{\prime }(x)\ne 0$ 这个条件意味着 $g^{\prime }(x)$ 要么恒为正, 要么恒为负, 所以函数是严格单调的. 特别地, 这说明 $g(a)\ne g(b)$, 从而上式右边是良好定义的.

尽管这个命题可能在一些较难的习题中大显身手, 但就本身的深刻程度而言不过是 Rolle 中值定理的一个无关痛痒的推广. 然而, 我们给出两个不同的证明并且解释怎么理解这个命题. 对一个命题有 (编) 一个感性的认识在学习数学中是非常重要的.

证明.

1.

我们定义如下的函数: $$F(x)=f(x)-f(a)-\frac{f(b)-f(a)}{g(b)-g(a)}(g(x)-g(a)).$$因为 $F(b)=F(a)=0$, 所以 Rolle 中值定理可用. 这是一个技术性的证明, 想法和 Lagrange 中值定理的证明如出一辙. (很多习题册上的题目都是根据这个想法来编的, 作业中我们会见到几个例子 (比较有技巧性, 但其实没有多大意思) ) .

2.

这个证明比第一个证明复杂很多, 然而在概念的层次上要更清晰也包含了更多的理解. 首先, 我们观察到如果 $g(x)=x$, 那么这个定理就是 Lagrange 中值定理. 证明的主旨是将一般的 $g$ 的情况化为这个已知情况, 只需要微分几何中一些最朴素的想法. 利用 $g^{\prime }(x)\ne 0$, 我们知道 $g:I=[a,b]\to J=[g(a),g(b)]$ 是同胚, 即连续的双射并且逆映射也是连续的. 我们需要将 $g$ 想成用 $I$ 来重新参数化 $J=[g(a),g(b)]$. 注记. 比方说, 给定 $\mathbb{R}$ 上的区间 $J=[0,1]$, 我们假设 $\mathbb{R}$ 上用的坐标是 $y$, 那么, 我们可以用 $y$ 来表示 (参数化) $I$ 中的点. 考虑映射$$g:[0,2]\to [0,1],x\mapsto \frac{x}{2}.$$此时, 我们可以用通过 $g$ 用 $x\in [0,2]$ 来 (参数化) 描述 $J$ 中的点: $x=1$ 对应的是 $J$ 中的 $0.5$ 这个点. 我们现在认为 $J=[g(a),g(b)]$ 是基本的几何对象. 本来 $f$ 是 $I$ 上的函数, 我们可以通过上述参数化将 $f$ (通过复合) 视作是 $[g(a),g(b)]$ 上的函数: $$JIY{g}^{-1}f\circ g^{-1}f$$我们要考虑 $f(g^{-1})(y)=f\circ g^{-1}$ 这个函数. 根据 Lagrange 中值定理 (对 $f\circ g^{-1}:J\to \mathbb{R}$ 来用) , 我们有$$\frac{f\circ g^{-1}(g(a))-f\circ g^{-1}(g(b))}{g(a)-g(b)}=(f\circ g^{-1}{)}^{\prime }(c).$$不难认出, 这就是要证明的等式. 这个证明表明, Cauchy 中值定理实际上是 Lagrange 中值定理在不同的参数化下的表述 (从这个角度看, $f$ 和 $g$ 的位置不是对等的) .

$\square$

另外, 我们会问这个定理直观上说了什么 (有没有比较容易记住的方式) ? 这里可以看出向量值函数的威力: 考虑映射$$F:[a,b]\to {\mathbb{R}}^2,x\mapsto \left(\genfrac{}{}{0ex}{}{f(x)}{g(x)}\right).$$这个映射的像是 ${\mathbb{R}}^2$ 上的一条曲线段. Cauchy 中值定理说的是存在曲线上的点 $x_0$, 使得其切线方向 $F^{\prime }(x_0)$ 和两个端点的连线 $\left(\genfrac{}{}{0ex}{}{f(b)}{g(b)}\right)-\left(\genfrac{}{}{0ex}{}{f(a)}{g(a)}\right)$ 是同方向的. 在图上看起来这与 Rolle/Lagrange 中值定理的几何直观是一致的. 事实上, 我们还可以定义$$\hat{F}:[a,b]\to {\mathbf{S}}^1,x\mapsto \frac{(f^{\prime }(x),g^{\prime }(x))}{\sqrt{f^{\prime }(x{)}^2+g^{\prime }(x{)}^2}}.$$这个是切线的方向的函数, 由于 $\left(\genfrac{}{}{0ex}{}{f(b)}{g(b)}\right)-\left(\genfrac{}{}{0ex}{}{f(a)}{g(a)}\right)$ 也决定了 ${\mathbf{S}}^1$ 中的一个方向, 这个定理的叙述变得类似于这种情况下的介值定理 (${\mathbf{S}}^1$ 是 $1$ 维的) . 此时, 我们很自然地看到为什么需要研究在其它空间上取值的函数 (映射) .

三角函数的研究

由于有了导数作为新的工具, 我们可以来研究 $\sin x$ 和 $\cos x$ 的周期性了. 三角函数是解析的方式来定义的, 即用级数来定义: $$\cos x=\sum _{k=0}^{\infty }\frac{(-1{)}^k{x}^{2k}}{(2k)!},\sin x=\sum _{k=0}^{\infty }\frac{(-1{)}^k{x}^{2k+1}}{(2k+1)!}.$$它们具有周期性是一个很深刻的事实. 我们令$$F:\mathbb{R}\to {\mathbb{R}}^2,x\mapsto F(x)=\left(\genfrac{}{}{0ex}{}{\sin x}{\cos x}\right).$$用 $J$ 表示矩阵 $J=\left(\genfrac{}{}{0ex}{}{01}{-10}\right)$. 那么, 根据 $(\cos x{)}^{\prime }=-\sin x$ 和 $(\sin x{)}^{\prime }=\cos x$, 我们发现 $F$ 满足如下的微分方程$$\{\begin{array}{ll}& F^{\prime }=JF,\\ & f{|}_{x=0}=\left(\genfrac{}{}{0ex}{}{0}{1}\right).\end{array}$$我们还把 $F(x)$ 写成$$F(x)=(S(x),C(x)),S(x)=\sin (x),C(x)=\cos (x).$$

注记. 如果你采取其它方式定义 $\sin x$ 和 $\cos x$ 的话, 比如说按照中学的方式定义的 $\sin x$ 和 $\cos x$, 你应该也能证明 $\sin x$ 和 $\cos x$ 满足上述的关系, 根据解的唯一性, 我们就知道这两种定义方式是一致的.

三角函数的解析表达式没有给出它们更多的信息, 我们利用函数的微分来研究 $\cos x$ 和 $\sin x$ 在 ${\mathbb{R}}_{⩾0}$ 上的行为:

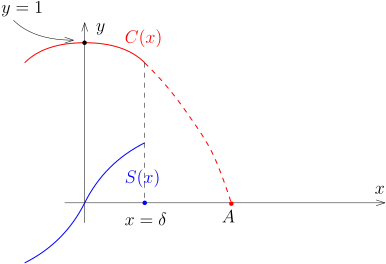
由于 $S^{\prime }(0)=C(0)=1$, 根据连续性, $S$ 在某个 $[-\delta ,\delta ]$ 上面是严格递增的 ($\delta$ 是较小的正数) . 在区间 $(0,\delta )$ 上, 由于 $C^{\prime }(x)=-S(x)<0$, 从而, $C(x)$ 是严格递减的; 在区间 $(-\delta ,0)$ 上, 由于 $S(x)<0$, 从而 $C(x)$ 是严格递增的. 这表明 $0$ 是 $C(x)$ 的一个局部最大点 (这不意外, 因为 $|C(x)|⩽1$ 且 $C(0)=1$) . 这一段推导可以用如下的图像来表示:

我们下面要证明说一定能找到一个 $A>0$, 使得在 $[0,A]$ 上, $C(x)$ 是单调递减的并且在 $A$ 处 $C(x)$ 变成了 $0$. 考虑使得 $C$ 在 $[0,A)$ 上都 $>0$ 的最大可能的 $A$.

我们先说明 $A\ne +\infty$. 如若不然, 如果 $S^{\prime }=C>0$, 所以 $S$ 是 $(0,+\infty )$ 是严格递增的函数. 在 $x=\delta$, 我们令 $s=S(\delta )>0$, 从而, 当 $x⩾\delta$ 时, $S(x)⩾s>0$. 我们考虑如下的代数变形 (此时, 如果有积分的语言的话会更自然) : $$S(x)⩾s\iff (C(x)+sx{)}^{\prime }<0.$$这是把一个表达式写成全微分的技巧. 这表明函数 $C(x)+sx$ 在 $[\delta ,\infty )$ 上递减, 所以, 对任意的 $x⩾\delta$, 由于我们假设了 $C(x)>0$, 所以我们有$$C(\delta )+s\delta ⩾C(x)+sx>sx.$$令 $x\to +\infty$, 这自然是不可能的!

此时, 上面所描述的 $A<\infty$ 存在. 根据连续性, 在 $A$ 处, 有 $C(A)=0$. 根据 $C{|}_{[0,A]}⩾0$, 我们知道 $S$ 在 $[0,A]$ 上上升, 所以 $S(A)>0$. 我们现在计算 $S(A)$ 的值. 为此, 我们证明对任意满足上述微分方程的 $S(x)$ 和 $C(x)$, 都有 $(S(x){)}^2+(C(x){)}^2\equiv 1$. 证明是利用导数判别: 一个函数是常数当且仅当它的导数恒为零. $${\left((S(x){)}^2+(C(x){)}^2\right)}^{\prime }=2S(x)S^{\prime }(x)+2C(x)C^{\prime }(x)=0.$$而 $\left((S(x){)}^2+(C(x){)}^2\right){|}_{x=0}=1$. 据此, 我们知道 $S(A)=1$.

作为上面推导的总结, 我们知道存在常数 $A$, 使得 $S(0)=0$, $S(A)=1$ 并且 $S$ 在 $[0,A]$ 上严格递增; $C(0)=1$, $C(A)=0$ 并且 $C$ 在 $[0,A]$ 上严格递减.

重复上面的推导 (请同学自己补充细节) , 我可以找到 $B>0$, 使得 $S(A)=1$, $S(A+B)=0$ 并且 $S$ 在 $[A,A+B]$ 上严格递减; $C(A)=0$, $C(A+B)=-1$ 并且 $C$ 在 $[0,A]$ 上严格递减.

我们定义 $\overline{\pi }=A+B$, 按照上面的推导, 它是 $S(x)=\sin x$ 在正实轴上第一个零点.

此时, 考虑函数 $\left(\genfrac{}{}{0ex}{}{\overline{S}(x)}{\overline{C}(x)}\right)=-\left(\genfrac{}{}{0ex}{}{S(x+\pi )}{C(x+\pi )}\right)$. 很明显, $\left(\genfrac{}{}{0ex}{}{\overline{S}}{\overline{C}}\right)$ 和 $\left(\genfrac{}{}{0ex}{}{S}{C}\right)$ 解一样的微分方程 (同样的初值) , 所以根据唯一性, 我们得到$$S(x)=\overline{S}(x)=-S(x+\overline{\pi }),C(x)=\overline{C}(x)=-C(x+\overline{\pi }).$$从而, $$S(x)=S(x+2\overline{\pi }),C(x)=C(x+2\overline{\pi }).$$这说明 $2\overline{\pi }$ 是 $S$ 和 $C$ 的周期. 另外, $S$ 在 $[0,\overline{\pi }]$ 上面为正, 在 $[\overline{\pi },2\overline{\pi }]$ 上面为负. 这表明 $2\overline{\pi }$ 是 $S$ 的最小周期; 类似地, $2\overline{\pi }$ 是 $C$ 的最小周期.

脚注

1.	^ 上传者注: 事实上讲义上并没有提到, 疑似是课堂上提到过.