凸函数的性质和 Jensen 不等式
我们给出凸函数的五种刻画:
I 是 R 上的区间, 给定 I 上定义的实值函数 f:I→R. 那么, 五个性质是等价的:
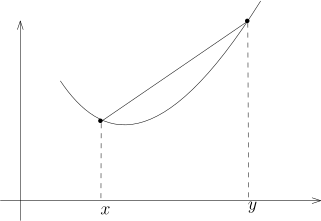
1) | 对任意的 x,y∈I, 任意的 t∈[0,1], 我们有f(tx+(1−t)y)⩽tf(x)+(1−t)f(y).从图形上来看, 任给 f 的图像上两个点, 这两个点之间的函数图像落在这两个点所连线段的下方. |
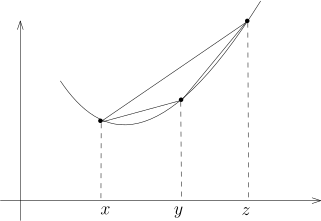
2) | 对任意的 x,y,z∈I, 如果 x<y<z, 那么y−xf(y)−f(x)⩽z−xf(z)−f(x)⩽z−yf(z)−f(y).我们可以通过函数图像形象的记忆这一串不等式: |
3) | 对任意 a∈I, 如下定义的函数I−{a}→R, x↦x−af(x)−f(a),是变量 x 的增函数. |
4) | 对任意的 x,y,z∈I, 如果 x<y<z, 那么det⎝⎛1xf(x)1yf(y)1zf(z)⎠⎞⩾0. |
5) | 集合 Γ⩾f={(x,y)∣∣x∈I,y⩾f(x)}⊂R2 (即函数图像上方的部分) 是凸集 |
如果函数 f 满足上述条件之一, 我们就称 f 是凸函数. 如果 −f 是凸函数, 我们就称 f 是凹函数.
V 是 R-线性空间, C⊂V 是子集. 如果对任意的 x,y∈C, 任意的 t∈[0,1], tx+(1−t)y∈C, 即 x 和 y 所连线段落在 C 中, 我们就称 C 是凸集.
上述对凸性的刻画本质上是几何的, 叙述中并没有涉及到函数的连续性等. 有意思的是, 凸性的几何定义可以推出函数的若干分析性质, 比如连续性、可微性之类的.
证明. 我们转一圈来证明前面四个命题之间的等价性:
1)⇒2) | 由于 y∈(x,z), 所以存在 t∈(0,1), 使得 y=tx+(1−t)z, 其中 t=x−zy−z. 所以, f(y)⩽tf(x)+(1−t)f(z)=x−zy−zf(x)+x−zx−yf(z).这个不等式等价于 2) 中的不等式 (直接计算) . |
2)⇔3) | 2) 中左侧的不等式讲的就是这个函数是递增的. |
3)⇒4) | 我们注意到det⎝⎛1xf(x)1yf(y)1zf(z)⎠⎞=(z−x)(y−x)(z−xf(z)−f(x)−y−xf(y)−f(x)).利用 3) 中的单调性, 这个值明显是非负的. |
4)⇒1) | 我们不妨设 x⩽y, 我们对下面的式子展开: det⎝⎛1xf(x)1tx+(1−t)yf(tx+(1−t)y)1yf(y)⎠⎞⩾0.这等价于(y−x)((1−t)(f(y)−f(x))−(f(tx+(1−t)y)−f(x)))⩾0.整理立得. |
最终, 我们来证明 5)⇔1) : 假设 Γ⩾f 是凸集, 那么对任意的 x,y∈I, 我们有 (x,f(x)),(y,f(y))∈Γ⩾f, 所以, 对任意的 t∈[0,1], 我们有(tx+(1−t)y,tf(x)+(1−t)f(y))∈Γ⩾f.按照 Γ⩾f 的定义, 我们有 f(tx+(1−t)y)⩽tf(x)+(1−t)f(y)).
反之, 假设 1) 成立, 任选
(x1,y1),(x2,y2)∈Γ⩾f, 按照定义
y1⩾f(x1),
y2⩾f(x2). 考虑这两个点所连线段上的任意一个点
(x,y)=t(x1,y1)+(1−t)(x2,y2), 其中
t∈[0,1]. 根据 1), 我们知道
f(x)⩽tf(x1)+(1−t)f(x2)⩽ty1+(1−t)y2=y,所以
(x,y)∈Γ⩾f.
根据等价定义中的第一条, 我们可以证明:
假设 f:I→R 是凸函数, 那么对任意的 x1,⋯,xn∈I 和任意的 t1,⋯,tn∈[0,1], 其中 t1+t2+⋯+tn=1, 我们有f(t1x1+⋯+tnxn)⩽t1f(x1)+⋯+tnf(xn).
证明. 我们对
n 进行归纳.
n=2 时, 这是定义; 假设对
n 成立, 考虑
n+1 的情形. 对任意给定的
x1,⋯,xn+1∈I,
t1,⋯,tn+1∈[0,1], 其中
t1+t2+⋯+tn+1=1, 我们有
f(t1x1+⋯+tnxn+tn+1xn+1)=f((1−tn+1)1−tn+1t1x1+⋯+tnxn+tn+1xn+1).不难看出,
1−tn+1t1x1+⋯+tnxn∈I, 此时我们用等价定义中的第一条, 就得到
f(t1x1+⋯+tnxn+tn+1xn+1)⩽(1−tn+1)f(1−tn+1t1x1+⋯+1−tn+1tnxn)+tn+1f(xn+1)⩽(1−tn+1)(1−tn+1t1f(x1)+⋯+1−tn+1tnf(xn))+tn+1f(xn+1)=t1f(x1)+⋯+tn+1f(xn+1).这就完成了证明.
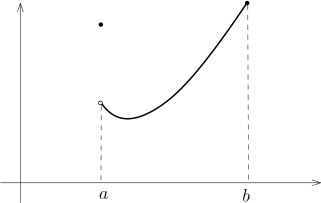
一个凸函数可以不连续, 比如说下图所示的函数
它在左端点处不连续. 然而, 这是一个凸函数可能不连续的唯一方式:
I⊂R 是区间, f:I→R 是凸函数, 我们令 I˚ 为 I 的内部 (对于 I=[a,b],[a,b),(a,b] 或 (a,b), 那么 I˚=(a,b)) , 那么
1) | f∈C(I˚). |
2) | 对任意的 x0∈I˚, f 在 x0 处的左导数 f′−(x0) 和右导数 f′+(x0) 存在. 进一步, 它们满足f′−(x0)⩽f′+(x0). |
3) | 对任意的 x,y∈I˚, 如果 x<y, 那么我们有f′−(x)⩽y−xf(y)−f(x)⩽f′+(y). |
4) | 左右导数 f′±:I˚→R 是递增的函数. |
证明. 任意选定 x0∈I˚. 存在 h1,h2>0, x0−h1,x0+h2∈I˚, 对三个点 x0−h1,x0 和 x0+h2 用凸性的第二个等价定义, 我们得到h1f(x0)−f(x0−h1)⩽h2f(x0+h2)−f(x0),根据凸性的第三个等价定义, 由于上述不等式的右边是 h2 的增函数, 令 h2→0, 我们立即得到右导数的存在性; 类似地, 如果令 h1→0, 我们就得到左右导数存在性. 既然左右导数都存在, 那么, f 自然在 I˚ 上连续.
为了证明 3), 我们先令 h2→0, 从而, h1f(x0)−f(x0−h1)⩽f′+(x0),令 x0=y, x0−h1=x, 我们就得到了 3) 中不等式的右边; 左边类似可得.
为了证明 4), 我们考虑 3) 中的不等式
f′−(x)⩽x−zf(x)−f(z)⩽z−yf(z)−f(y),其中
x<z<y, 后一个不等式是运用凸性的第三个等价定义. 再令
z→y (
z<y) 就证明了结论.
上述分析性质基本上刻画了凸函数:
假设 I 是开区间, f:I→R 是函数. 如下两个性质等价:
1) | f 是凸函数; |
2) | f 是连续函数, f 的右导数处处存在并且是增函数. |
证明. 只要说明 2)⇒1) 即可: 我们固定 I 中的三个点 x<y<z, 对任意的 t∈[y,z], 我们有 f′+(y)⩽f′+(t)⩽f′+(z). 我们定义函数g:[y,z]→R, t↦f(t)−tf′+(y).那么, 对于 t∈(y,z), g 在 t 处的右导数 g′+(t)=f′+(t)−f′+(y)⩾0. 把这个和导数的性质做类比, 我们想说明 g 是 t∈(y,z) 的增函数:
假设 g:[a,b]→R 是连续函数并且右导数在每个点处都定义. 如果对任意的 t∈(a,b), 我们都有 g′+(t)⩾0, 那么 g(a)⩽g(b).
先假设引理是成立的, 那么我们有
g(z)⩾g(y), 经过整理, 我们得到
f′+(y)⩽z−yf(z)−f(y).类似地, 我们可以证明
f′+(y)⩾y−xf(y)−f(x).从而,
y−xf(y)−f(x)⩽z−yf(z)−f(y).所以, 我们有
det⎝⎛1xf(x)1yf(y)1zf(z)⎠⎞=det⎝⎛1xf(x)0y−xf(y)−f(x)0z−yf(z)−f(y)⎠⎞⩾0.这表明
f 是凸函数.
引理的证明. (证明的重要想法: 退 ε-步海阔天空) 任意选定 ε>0, 令φε:[a,b]→R,x↦−(g(x)−g(a))−ε(x−a).此时, φε′+⩽−ε<0, 我们实质上想证明这是一个递减的函数, 如果成立的话, 那么φε(a)⩾φε(b) ⇒ 过渡的结论0⩾φε(b) ⇒ g(b)−g(a)⩾−ε(b−a).令 ε→0 就得到了要证明的结论.
我们现在直接证明上述过渡的结论. 为此, 定义 1Xε1={x∈[a,b]∣∣φε(x)⩽ε1}由于 Xε1=[a,b]∩(φε)−1((−∞,ε1]) 是闭集, 所以它的上确界 c=supXε1∈Xε1. 我们想证明 b∈X (从而, ε1⩾φε(b), 令 ε1→0, 过渡性结论就成立了) , 即要证明 c=b.
因为 φε(a)=0, 所以 a∈Xε1. 特别地, 根据 φε(x) 的连续性, 存在 δ>0, 使得 [a,a+δ)⊂Xε1. 所以 Xε1=∅ 并且 c>a.
我们用反证法证明 c=b: 如若不然, 我们假设 c<b. 先说明 φε(c)=ε1, 这因为按照定义 φε(c)⩽ε1, 如果等号不成立, 那么 φε(c)<ε1, 根据 φε(x) 的连续性, 存在比 c 略大的数使得其值仍然不超过 ε1, 这就与 c=supXε1 矛盾.
其次根据右导数的信息,
φε′+(c)⩽−ε, 利用右导数的定义, 存在
h0>0, 使得当
h∈[0,h0) 时, 我们有
hφε(c+h)−φε(c)<−21ε.从而,
φε(c+h)<ε1−21εh<ε1.这表明
[c,c+h0)⊂Xε, 这和
c 是上确界矛盾.
假设 I⊂R 是开区间, f 是 I 上二次可微的实值函数. 如下两个陈述是等价的:
这个推论是最常用的来判断凸性的工具, 因为函数二阶导数通常容易计算.
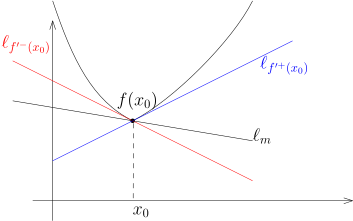
f:I→R 是区间 I 上的凸函数, x0∈I˚. 考虑 R2 上的过 (x0,f(x0)) 直线ℓm={(x,y)∈R2∣y=m(x−x0)+f(x0)},其中斜率 m∈R. 那么, ℓm 在 f 的图像之下当且仅当 f′−(x0)⩽m⩽f′+(x0).
证明. 定理的证明过程表明, 当 x>x0 时, 我们有f′+(x0)⩽x−x0f(x)−f(x0) ⇒ f(x)⩾f(x0)+(x−x0)f′+(x0).反过来, 当 x<x0 时, 我们有f(x)⩾f(x0)+(x−x0)f′−(x0).据此, 当 m⩽f′+(x0) 时, 在 x0 的右边, 该直线在 f 的图像之下; 当 m⩾f′−(x0) 时, 在 x0 的做边, 该直线在 f 的图像之下.
反之, 假设
ℓm 在
f 的图像之下, 在
x0 处的右边的时候, 我们有
f(x)⩾m(x−x0)+f(x0), 从而
f′+(x0)=x→x0+limx−x0f(x)−f(x0)⩾m.类似地, 我们可以证明另一边的不等式.
用凸函数证明常见的不等式
我们给出两个例子: Minkowski 不等式和算术-几何平均值不等式.
1) | 假设 p⩾1, 对于 x∈[0,1], 函数 f(x)=(1−xp1)p 是凸函数, 这因为f′(x)=−xp1−1(1−xp1)p−1是递增的函数 (求两次导数的表达式不是很简单) . 假设 ai,bi∈R⩾0 并且假设 ai+bi=0, 其中 i=1,2,⋯,n. 我们令xi=(ai+bi)paip, ti=k=1∑n(ak+bk)p(ai+bi)p.Jensen 不等式给出了如下所谓的 Minkowski 不等式: (k=1∑n(ak+bk)p)p1⩽(k=1∑nakp)p1+(k=1∑nbkp)p1.作为推论, 对于线性空间 V=Rn, 我们定义∥x∥p=(k=1∑nxkp)p1,其中, x=(x1,⋯,xp). 此时, Minkowski 不等式讲的是∥x∥p+∥y∥p⩾∥x+y∥p.这表明 ∥x∥p 是范数 (p=2 或者 1 我们更熟悉) . 另外, 我们还可以采取如下的范数: ∥x∥∞=k⩽nsup∣xk∣. |
2) | 函数 −logx 是 R>0 上的凸函数, 这因为(−logx)′′=x21⩾0假设 x1,⋯,xn 是正数, 根据 Jensen 不等式, 我们有−log(n1x1+⋯+n1xn)⩽−n1log(x1)−⋯−n1log(xn).这个等价于算术-几何平均值不等式: n1(x1+⋯+xn)⩾(x1⋯xn)n1. |