47. 子流形上的积分计算, Stokes 定理

Fubini 公式的一个应用

先补充 Fubini 公式的一个应用:

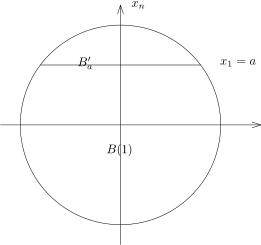
例子. 令 $c_n=m(B(1)\subset {\mathbb{R}}^n)$ 为 ${\mathbb{R}}^n$ 中单位球的体积, 我们来计算所有的 $c_n$. 对于 $n⩾1$, 我们令$$B_a^{\prime }=B(1)\cap \{x_n=a\}.$$它的半径长为 $\sqrt{1-a^2}$

此时, 我们有$$\begin{array}{rl}{c}_n& =m(B(1))={\int }_{-1}^{1}m(B_{x_n}^{\prime })d{x}_n\\ & =2{\int }_0^1(1-x_n^2{)}^{\frac{n-1}{2}}{c}_{n-1}d{x}_n\\ & =2c_{n-1}{\int }_0^{\frac{\pi }{2}}{\sin }^n\theta d\theta .\end{array}$$其中, 我们用了变元替换 $x_n=\cos \theta$. 我们注意到, $I_n={\int }_0^{\frac{\pi }{2}}{\sin }^n\theta d\theta$ 是我们上个学期研究过的 Wallis 积分, 其中, $$I_{2p}=\frac{(2p)!}{2^{2p}(p!{)}^2}\frac{\pi }{2},I_{2p+1}=\frac{2^{2p}(p!{)}^2}{(2p+1)!}.$$从而, 我们可以递归地计算 $c_n$. 特别地, 我们有$$c_{2n}=\frac{{\pi }^n}{n!}.$$根据递归公示, 我们很容易证明$$\underset{n\to \infty }{\lim }{c}_n=0.$$这说明当 $n$ 变大时, ${\mathbb{R}}^n$ 中单位球的体积趋于 $0$. 另外, 如果借助计算器的话, 我们可以很快看到 $c_5$ 是最大的.

我们上次课讲过, 如果给定函数图像 ${\Gamma }_f$, 那么它上面的积分可以用如下的公式来计算: $${\int }_{{\Gamma }_f}\phi d\sigma ={\int }_{{\mathbb{R}}^{n-1}}\phi (x,f(x))\sqrt{1+|\nabla f(x){|}^2}dx.$$

我们现在来看几个经典的例题:

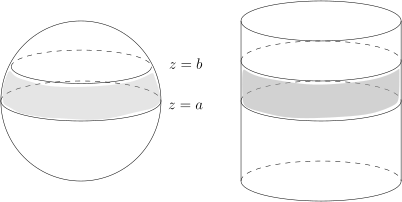
例子 (Archimedes). 考虑 ${\mathbf{S}}^2\subset {\mathbb{R}}^3$ 是标准的单位球面, 对于 $a,b\in [-1,1]$, 我们令$${\mathbf{S}}^2(a,b)=\{(x,y,z)\in {\mathbf{S}}^2|a⩽z⩽b\}.$$我们令 $\mathbf{C}$ 为与 $z$-轴平行的圆柱面, 并且这个圆柱面的直径是 $2$ (恰好可以套在 ${\mathbb{S}}^2$ 上) . 对于 $a,b\in [-1,1]$, 我们令$$\mathbf{C}(a,b)=\{(x,y,z)\in {\mathbb{R}}^3|x^2+y^2=1,a⩽z⩽b\}.$$

这是两个平行的平面在 ${\mathbf{S}}^2$ 或者 $\mathbf{C}$ 上所截出的带状区域 (图中的灰色区域) . Archimedes 的一个著名定理说, ${\mathbf{S}}^2(a,b)$ 的面积和 $\mathbf{C}(a,b)$ 的面积相等. 我们来证明这个命题.

我们不妨假设 $a=0,b>0$ (从这一点出发很容易证明 Arichmedes 的定理, 这是因为我们将看到 $\mathbf{C}(a,b)$ 的面积正比于 $b-a$) , 此时, ${\mathbf{S}}^2(a,b)$ 可以写成函数的图像: $${\mathbf{S}}^2(0,b)=\{(x,y,z)\in {\mathbb{R}}^3|z=\sqrt{1-x^2-y^2},1⩾x^2+y^2⩾1-b^2\}.$$此时, $f(x,y)=\sqrt{1-x^2-y^2}$, 所以$$d\sigma =\sqrt{1+|\nabla f(x){|}^2}dxdy=\sqrt{\frac{1}{1-x^2-y^2}}dxdy.$$所以, $$\begin{array}{rl}\sigma ({\mathbf{S}}^2(0,b))& ={\int }_{1⩾x^2+y^2⩾1-b^2}\sqrt{\frac{1}{1-x^2-y^2}}dxdy\\ & ={\int }_{\sqrt{1-b^2}}^1{\int }_0^{2\pi }\sqrt{\frac{1}{1-r^2}}rd\theta dr\\ & =2\pi {\int }_{\sqrt{1-b^2}}^1\sqrt{\frac{1}{1-r^2}}rdr\\ & =\pi {\int }_{1-b^2}^1\sqrt{\frac{1}{1-t}}dt\\ & =-2\pi \sqrt{1-t}{|}_{1-b^2}^1=2\pi b.\end{array}$$

现在计算 $\mathbf{C}(0,b)$ 的面积, 由对称性, 我们把 $x$ 看成是 $y$ 和 $z$ 的函数, 有对称性, 我们假设 $x⩾0$, 所以, 只要算如下图形的面积即可: $${\mathbf{C}}^{+}(0,b)=\{(x,y,z)\in {\mathbb{R}}^3|x=\sqrt{1-y^2},-1⩽y⩽1,0⩽z⩽b\}.$$所以, 我们有 $f(y,z)=\sqrt{1-y^2}$, 从而, $$d\sigma =\sqrt{\frac{1}{1-y^2}}dydz.$$所以, $$\begin{array}{rl}\sigma ({\mathbf{C}}^{+}(0,b))& ={\int }_{[-1,1]\times [0,b]}\sqrt{\frac{1}{1-y^2}}dydz\\ & =b{\int }_{-1}^1\sqrt{\frac{1}{1-y^2}}dy\\ & =b\pi .\end{array}$$从而, $$\sigma (\mathbf{C}(0,b))=2\sigma ({\mathbf{C}}^{+}(0,b))=\sigma ({\mathbf{S}}^2(0,b)).$$

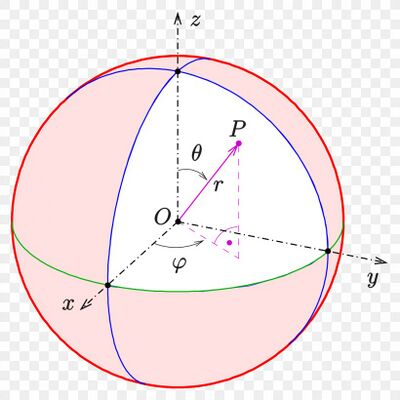
我们还可以采取参数化的形式来计算 ${\mathbf{S}}^2(a,b)$ 的面积, 比如说, 我们可以利用球面坐标系: $$\Phi :(0,\pi )\times (0,2\pi )\to {\mathbf{S}}^2,(\theta ,\phi )\mapsto (\sin (\theta )\cos (\phi ),\sin (\theta )\sin (\phi ),\cos (\theta )).$$

由于 $z=\cos \theta$, 所以 ${\mathbf{S}}^2(a,b)$ 由 $\theta \in [\arccos b,\arccos a]$ 所定义. 此时, 我们有$${}^t\mathrm{Jac}(\Phi )=\left(\begin{array}{ccc}\cos \theta \cos (\phi )& \cos \theta \sin (\phi )& -\sin \theta \\ -\sin \theta \sin (\phi )& \sin \theta \cos (\phi )& 0\end{array}\right)\Rightarrow \det G_{\Phi }={\sin }^2\theta .$$所以, $d\sigma =\sin \theta d\theta d\phi$, 从而$$\begin{array}{rl}\sigma ({\mathbf{S}}^2(0,b))& ={\int }_{(0,\pi )\times (0,2\pi )}\sin \theta d\theta d\phi \\ & =2\pi {\int }_{\arccos b}^{\arccos a}\sin \theta d\theta \\ & =2\pi (b-a).\end{array}$$

我们可以类似地计算 $\mathbf{C}(0,b)$ 的面积, 考虑参数化$$\Phi :(0,2\pi )\times (a,b)\to \sigma (\mathbf{C}(0,b)),(\theta ,s)\mapsto (\cos (\theta ),\sin (\theta ),s).$$从而, $${}^t\mathrm{Jac}(\Phi )=\left(\begin{array}{ccc}-\sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right)\Rightarrow \det G_{\Phi }=1.$$所以, $d\sigma =d\theta ds$, 从而$$\sigma (\mathbf{C}(0,b))={\int }_{(0,2\pi )\times (a,b)}d\theta ds=2\pi (b-a).$$

Stokes 公式

我们先给出 Stokes 公式的第一个证明, 其想法是把整体的公式转换为局部上的公式. 为此, 我们先证明一种特殊形式的单位分解定理, 这是一个技术性的引理.

注记 (截断函数的存在性). 我们在上个学期作业七习题 F 中 (截断函数部分) 构造了函数 $\psi (x)\in C^{\infty }(\mathbb{R})$, 使得 $\psi (x)⩾0$, 在 $[-1,1]$ 上恒为 $1$, 在 $[-2,2]$ 之外恒为零. 另外, 这个 $\psi$ 还是偶函数, 并且在 $[1,2]$ 之间是单调下降的.

我们现在来构造 ${\mathbb{R}}^n$ 上的光滑截断函数 $\phi (x)\in C^{\infty }({\mathbb{R}}^n)$, 其中$$\phi (x)=\psi (x_1^2+\cdots +x_n^2)=\psi (r^2).$$

很明显, $\phi$ 只依赖于变量 $r$, 它半径为 $2$ 的球之外恒为 $0$, 在半径为 $1$ 的球之上恒为 $1$ 并且这是一个对于半径 $r$ 递减的函数.

我们还可以构造 ${\mathbb{R}}^n$ 上的光滑截断函数 $\chi (x)\in C^{\infty }({\mathbb{R}}^n)$, 其中$$\chi (x)=\psi (x_1)\psi (x_2)\cdots \psi (x_n).$$

很明显, 这个函数是光滑的正函数, 它在一个中心在原点并且边长为 $2$ 的正方体上恒为 $1$, 在中心在原点并且边长为 $4$ 的正方体之外恒为 $0$.

我们强调, 这类函数具体构造并不重要, 我们只用上面所列举的几条性质.

我们要构造一个与格点 ${\mathbb{Z}}^n\subset {\mathbb{R}}^n$ 相容的单位分解. 为此, 首先定义 ${\mathbb{R}}^n$ 上的函数: $$F(x)=\sum _{(k_1,\cdots ,k_n)\in {\mathbb{Z}}^n}\chi (x_1+k_1,\cdots ,x_n+k_n).$$这个函数是良好定义的: 对于给定的 $x=(x_1,\cdots ,x_n)\in {\mathbb{R}}^n$, 这是一个有限和, 因为当某个 $|k_i+x_i|⩾2$ 时, $\chi (x_1+k_1,\cdots ,x_n+k_n)=0$, 所以, 有贡献的项只是 ${\mathbb{Z}}^n$ 与中心在 $x$ 处边长为 $4$ 的正方体中的格点, 这自然是一个有限集.

特别地, $F$ 是光滑函数并且以 ${\mathbb{Z}}^n$ 为周期的周期函数, 即对任意的 $(k_1,\cdots ,k_n)\in {\mathbb{Z}}^n$, 我们有$$F(x_1+k_1,\cdots ,x_n+k_n)=F(x_1,\cdots ,x_n).$$

另外, 根据 $\chi$ 的构造, 对任意的 $x$, 我们都有 $F(x)>0$. 据此, 对每个 $\mathbf{k}=(k_1,\cdots ,k_n)\in {\mathbb{Z}}^n$, 我们可以定义$$F_{\mathbf{k}}(x_1,\cdots ,x_n)=\frac{\chi (x_1-k_1,\cdots ,x_n-k_n)}{F(x)},$$我们得到了一组有紧支集 ¹的光滑函数 $F_{\mathbf{k}}$, 使得对任意的 $x\in {\mathbb{R}}^n$, 我们有$$\sum _{\mathbf{k}\in {\mathbb{Z}}^n}{F}_{\mathbf{k}}(x)=1.$$对任意的 $\mathbf{k}\in \mathbb{Z}$, $F_{\mathbf{k}}$ 在某个中心在格点上面并且边长为 $4$ 的正方体之外恒为 $0$ (本来在某个小一点的正方体上恒为 $1$ 的性质由于除以 $F$ 所以不再成立) .

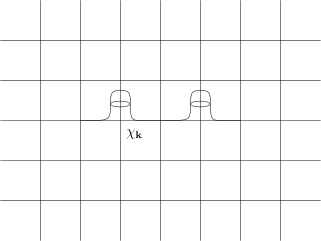
我们现在任意固定一个 (很大的) 正整数 $N⩾1$. 对每个 $\mathbf{k}\in \mathbb{Z}$, 我们定义$${\chi }_{\mathbf{k}}(x)=F_{\mathbf{k}}(2^{N+1}x).$$那么, ${\chi }_{\mathbf{k}}$ 在某个边长为 $2^{-N}$ 的正方体上恒为 $1$, 把这个正方体扩大一倍之后 (边长为 $2^{-N+1}$) , ${\chi }_{\mathbf{k}}$ 在这个大正方体之外恒为 $0$. 特别地, 这两个正方体的中心落在 $2^{-N+1}{\mathbb{Z}}^n$ 中 (这是更密的格点) . 我们自然还有$$\sum _{\mathbf{k}\in {\mathbb{Z}}^n}{\chi }_{\mathbf{k}}\equiv 1.$$综合上面的讨论, 我们得到了如下的单位分解定理, 其中, 所谓的单位分解, 指的是把 $1$ 这个单位函数分解成若干函数的和:

引理 47.1 (周期的单位分解). 对任意的 $N⩾1$, 令 ${\Gamma }_N=2^{-(N+1)}{\mathbb{Z}}^n$. 那么, 存在一族有紧支集的非负的光滑函数 $\{{\chi }_{\mathbf{k}}(x){\}}_{\mathbf{k}\in {\Gamma }_N}$, 满足如下的两个条件:

1)	对任意的 $\mathbf{k}\in {\Gamma }_N$, $\mathrm{supp}{\chi }_{\mathbf{k}}$ 落在以 $\mathbf{k}$ 为中心边长为 $2^{-N+1}$ 的正方体中;
3)	常值函数 $1$ 可以分解为: $$1=\sum _{\mathbf{k}\in {\Gamma }_N}{\chi }_{\mathbf{k}}.$$

为了证明 Stokes 定理, 我们还需要技术性的引理. 这个引理实际上大有渊源, 它和 Dirac $\delta$-函数有关, 我们会在下个学期的课程中经常用到这个引理.

引理 47.2. 假设 $\chi (x)$ 是 ${\mathbb{R}}^1$ 上的有紧支集的光滑函数, 我们假设 ${\int }_{{\mathbb{R}}^1}\chi (x)dx=1$. 那么, 对任意的连续函数 $f(x)$, 我们都有$$\underset{\epsilon \to 0^{+}}{\lim }\left({\int }_{\mathbb{R}}\frac{1}{\epsilon }\chi \left(\frac{x}{\epsilon }\right)f(x)dx\right)=f(0).$$

证明. 我们假设 $\mathrm{supp}(\chi )\subset [-M,M]$. 根据变量替换公式, 对任意的 $\epsilon >0$, 我们有$${\int }_{\mathbb{R}}\frac{1}{\epsilon }\chi \left(\frac{x}{\epsilon }\right)dx=1.$$为了证明引理所要求的极限, 我们做差: $$\begin{array}{rl}\left|{\int }_{\mathbb{R}}\frac{1}{\epsilon }\chi \left(\frac{x}{\epsilon }\right)f(x)dx-f(0)\right|& =\left|{\int }_{\mathbb{R}}\frac{1}{\epsilon }\chi \left(\frac{x}{\epsilon }\right)f(x)dx-f(0){\int }_{\mathbb{R}}\frac{1}{\epsilon }\chi \left(\frac{x}{\epsilon }\right)dx\right|\\ & =\left|{\int }_{\mathbb{R}}\frac{1}{\epsilon }\chi \left(\frac{x}{\epsilon }\right)(f(x)-f(0))dx\right|\\ & =\left|{\int }_{-\epsilon M}^{\epsilon M}\frac{1}{\epsilon }\chi \left(\frac{x}{\epsilon }\right)(f(x)-f(0))dx\right|.\end{array}$$由于 $f$ 在 $0$ 处连续, 所以对任意的 $ϵ>0$, 存在 $\delta >0$, 使得当 $|x|<\delta$ 时, $|f(x)-f(0)|<ϵ$. 所以, 当 $\epsilon <\frac{\delta }{M}$ 时, 上面的积分可以被下面的积分控制: $$\begin{array}{rl}\left|{\int }_{\mathbb{R}}\frac{1}{\epsilon }\chi \left(\frac{x}{\epsilon }\right)f(x)dx-f(0)\right|& ⩽{\int }_{-\epsilon M}^{\epsilon M}\frac{1}{\epsilon }\chi \left(\frac{x}{\epsilon }\right)ϵdx=ϵ.\end{array}$$所以, 所要证明的极限成立.

$\square$

为了能够正确地陈述与证明 Stokes 公式, 我们需要引入 ${\mathbb{R}}^n$ 中的 (有界) 带边的光滑区域 (或者 $C^1$-光滑) 的概念. 很多教科书上在 Stokes 的证明方面语焉不详, 很大程度上受制于没有正确地引入概念.

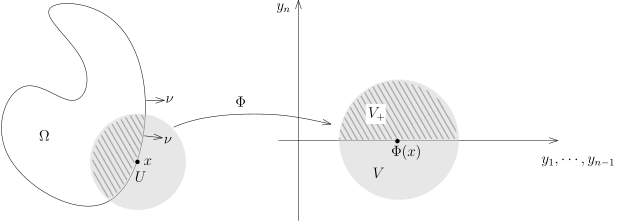
定义 47.3 (有界带边光滑区域). 给定 ${\mathbb{R}}^n$ 中的紧集 $\Omega \subset {\mathbb{R}}^n$, 我们假设对任意的 $x\in \Omega$, 如下两种情况必居其一:

1)	$x$ 是一个内点, 即存在开集 $U\subset \Omega$, 使得 $x\in U$;
2)	$x$ 是一个边界点, 即存在开集 $U\subset {\mathbb{R}}^n$, $x\in U$, 存在开集 $V\in {\mathbb{R}}^n$, 存在微分同胚 $\Phi :U\to V$, 其中 $U$ 上的坐标我们用 $x_1,\cdots ,x_n$ 表示, $V$ 上的坐标我们用 $y_1,\cdots ,y_n$ 表示使得 ∘ $\Phi (U\cap \Omega )=V_{+}=V\cap \{(y_1,\cdots ,y_n)\mid y_n⩾0\}$; ∘ $\Phi (x)$ 的 $y_n$ 坐标是 $0$.

那么, 我们把 $\Omega$ 称做是一个有界带边光滑区域. 我们总是约定 $\Omega$ 的内点的集合非空.

注记. 根据定义, 一个边界点绝对不能是内点, 因为它的任何一个领域都与 ${\Omega }^c$ 相交. 我们将 $\Omega$ 所有内点的集合记为 $\mathring{\Omega }$, 边界点的集合记作 $\partial \Omega$. 所以, $\Omega =\mathring{\Omega }\cup \partial \Omega$ 并且 $\mathring{\Omega }\cap \partial \Omega =\varnothing$.

在边界点的定义中, $\Phi$ 将边界点映射到 $V_{+}$ 的边界上, 即 ${\Phi }^{-1}(V_{+}\cap \{y_n=0\}\})\subset \partial \Omega$.

实际上, $\partial \Omega$ 是余维数为 $1$ 的光滑子流形. 证明是直截了当的: 局部上 (在上述定义中的 $U$ 中) , $x\in \partial \Omega$ 都被一个微分同胚映射成了 $V$ 中 $y_n=0$ 的点, 按照子流形的定义, 这是 $n-1$ 维的子流形.

对于 ${\mathbb{R}}^n$ 中的余维数为 $1$ 的光滑子流形 $M$, 对任意的 $x\in M$, 我们可以找到两个单位长的 (法) 向量 $\pm \nu$, 使得它们和 $T_{x}M$ 是垂直的.

引理 47.4. 假设 $\Omega$ 是一个有界带边光滑区域. 对于任意的 $p\in \partial \Omega$, 存在唯一的 $\nu (p)\in T_p{\mathbb{R}}^n={\mathbb{R}}^n$, 使得

1)	这是 $\partial \Omega$ 的单位法向量, 即 $\nu (p)\perp T_p\partial \Omega$ 并且 $|\nu (p)|=1$;
2)	这个向量指向 $\Omega$ 的外部, 即存在 $\epsilon >0$, 使得对任意的 $t\in (0,\epsilon )$, $p-t\nu (p)\in \Omega$.

我们称 $\nu (p)$ 是 $\Omega$ 在 $p\in \partial \Omega$ 处的单位外法向量.

证明. 按照定义, 存在开集 $p\in U\subset {\mathbb{R}}^n$, $V\in {\mathbb{R}}^n$ 和微分同胚 $\Phi :U\to V$, 使得 $x\in U$ 并且 $\Phi (\partial \Omega \cap U)=V\cap \{y_n=0\}$ 并且 $\Phi (U\cap \Omega )=V_{+}$. 如果我们令$$f:U\to \mathbb{R},x\mapsto f(x)={\Phi }^{\ast }{y}_n=y_n(\Phi )={\Phi }_n(x),$$其中 $\Phi (x)=({\Phi }_1(x),\cdots ,{\Phi }_n(x))$. 那么, $f$ 的零点集就定义了 $\partial \Omega$ 而且$$\Omega =\{x\in U|f(x)⩾0\}.$$此时, 我们任意选取 $\mathbf{n}(p)$, 使得 $\mathbf{n}(p)\perp T_p\partial \Omega$ 并且 $|\mathbf{n}(p)|=1$. 为了决定到底哪一个 $\pm \mathbf{n}(p)$ 是外法向量, 利用如下的性质$${\nabla }_{\mathbf{n}(p)}f(p)\ne 0.$$(否则对任意的 $v\in {\mathbb{R}}^n$, ${\nabla }_{v}f=0$, 从而 $df(p)=0$, 矛盾) 通过选取 $\mathbf{n}$ 前面的符号, 我们要求 $({\nabla }_{\nu }(p)f)(p)<0$. 此时, 对较小的 $\epsilon >0$, 对任意的 $t\in (0,\epsilon )$, 我们有$$f(p-t\nu (p))=f(p)-t\left({\nabla }_{\nu (p)}f\right)(p)+O(t^2)>0.$$这表明 $p-t\nu (p)\in \Omega$.

$\square$

注记. 假设 $\Omega$ 是一个有界带边光滑区域, 对任意的 $x\in \partial \Omega$, 我们都可以唯一地指定它的外法向量 $\nu (x)$, 所以, 我们有映射$$\nu :\partial \Omega \to {\mathbb{R}}^n,x\mapsto \nu (x).$$这实际上是光滑子流形 $\partial \Omega$ 上定义的光滑函数: 这是因为每个余 1 维子流形局部上都可以写成函数图像的形式 ², 从而我们可以用下面例子的结论.

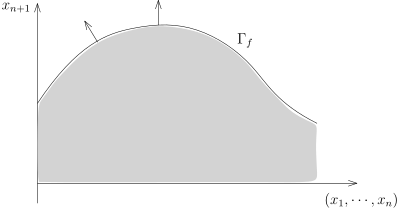
例子. 给定 ${\mathbb{R}}^n$ 上的光滑函数 $f:{\mathbb{R}}^n\to \mathbb{R}$, 我们把 $\Omega \subset {\mathbb{R}}^{n+1}$ 定义为 $f$ 的图像 ${\Gamma }_f$ 下的区域 (下面图中的灰色区域) , 即$$\Omega =\{(x,x_n)|x\in {\mathbb{R}}^n,x_n\in \mathbb{R},x_{n+1}⩽f(x)\}.$$我们计算 $\Omega$ 的单位外法向量 (我们注意到 $\Omega$ 不是有界区域, 但是这不影响我们计算法向量) .

证明. 很明显, $\partial \Omega ={\Gamma }_f$. 给定 $(x,f(x))\in \partial \Omega$, 其中 $x\in {\mathbb{R}}^n$, 我们已经计算过$$T_{(x,f(x))}\partial \Omega =\mathrm{span}\{e_1,\cdots ,e_n\},\text{其中}{e}_i=(\underset{\text{第 i 个位置处为 1，其余为 0}}{\underbrace{0,\cdots ,0,1,0,\cdots ,0}},\frac{\partial f}{\partial x_i}(x)).$$据此, 这个点处的单位外法向量必然是$$\nu =\pm \frac{1}{(1+|\nabla f{|}^2{)}^{\frac{1}{2}}}(-\nabla f,1)$$我们现在确定 $\nu$ 的符号: 考虑 $h(x_1,\cdots ,x_n)=x_{n+1}-f(x_1,\cdots ,x_n)$, 那么, $\Omega =h^{-1}((-\infty ,0])$. 为了保证 $\nu$ 是外法向量, 我们需要 ${\nabla }_{\nu }h>0$. 我们计算$${\nabla }_{\frac{(-\nabla f,1)}{(1+|\nabla f{|}^2{)}^{\frac{1}{2}}}}h=(1+|\nabla f{|}^2{)}^{\frac{1}{2}}.$$所以, $$\nu =\frac{1}{(1+|\nabla f{|}^2{)}^{\frac{1}{2}}}(-\nabla f,1).$$特别地, 此时, $\nu$ 对 $x$ 是光滑依赖的.

$\square$

我们现在叙述并证明 Stokes 公式:

定理 47.5. 假设 $\Omega$ 是一个有界带边光滑区域, $\nu (x)=({\nu }_1(x),\cdots ,{\nu }_n(x))$ 为 $\partial \Omega$ 的单位外法向量, $d\sigma$ 为 $\partial \Omega$ 上的曲面测度. 对任意的 $\phi \in C^1({\mathbb{R}}^n,\mathbb{C})$, 我们有$${\int }_{\Omega }\frac{\partial \phi }{\partial x_i}(x)dx={\int }_{\partial \Omega }\phi (x){\nu }_i(x)d\sigma .$$如果用向量值的函数来写, 我们有$${\int }_{\Omega }\nabla \phi dx={\int }_{\partial \Omega }\phi \cdot \nu d\sigma .$$

证明. 证明分为四步, 前两步是准备工作:

第一步, 把 $\partial \Omega$ 写成若干个函数图像的并.

对于每个 $x\in \partial \Omega$, 存在开集 $U_x\subset {\mathbb{R}}^n$, 使得 $x\in U_x$, $\partial \Omega \cap U_x$ 是函数的图像, 即在 $U_x$ 上, 存在 $k⩽n$, 使得 $\partial \Omega$ 形如$$\partial \Omega \cap U_x=\{(x_1,\cdots ,x_n)|x_k=f(x_1,\cdots ,x_{k-1},x_{k+1},\cdots ,x_n)\}.$$由于 $\partial \Omega$ 是紧集, 所以存在有限个 $U_{x_1},\cdots ,U_{x_m}$, 使得 $\partial \Omega =U_{x_1}\cup \cdots \cup U_{x_m}$.

特别地, 对于足够大的 $N>0$, 如果一个边长为 $2^{-N+1}$ 的正方体 $Q$ 与 $\partial \Omega$ 的交非空, 那么, 存在 $x_i$, 使得 $Q\subset U_{x_i}$. (请参考上学期第 11 次课关于 Lebesgue 数的讨论)

第二步, 函数的局部化.

首先观察到, Stokes 公式的左右两边对于 $\phi$ 都是线性的. 我们利用单位分解将 $\phi$ 限制到更小的开集上去: 对任意的 $N⩾1$, 我们有一族有紧支集的非负的光滑函数 $\{{\chi }_{\mathbf{k}}(x){\}}_{\mathbf{k}\in {\Gamma }_N}$, 其中 ${\Gamma }_N=2^{-(N+1)}{\mathbb{Z}}^n$, 使得对每个 $\mathbf{k}\in {\Gamma }_N$, $\mathrm{supp}{\chi }_{\mathbf{k}}$ 落在以 $\mathbf{k}$ 为中心边长为 $2^{-N+1}$ 的正方体中并且: $$1=\sum _{\mathbf{k}\in {\Gamma }_N}{\chi }_{\mathbf{k}}.$$从而, $$\phi =\sum _{\mathbf{k}\in {\Gamma }_N}\underset{={\phi }_{\mathbf{k}}(x)}{\underbrace{{\chi }_{\mathbf{k}}(x)\phi (x)}}.$$此时, 每个 ${\phi }_{\mathbf{k}}$ 在以 $\mathbf{k}$ 为中心边长为 $2^{-N+1}$ 的正方体之外恒为 $0$. 由于 $\Omega$ 是紧集, 所以上述支集与 $\Omega$ 相交的函数的个数是有限个, 所以, 我们只要对这些函数来证明即可. 我们仍然用 $\phi$ 表示 ${\phi }_{\mathbf{k}}$, 上面的讨论容许我们假设 $\mathrm{supp}(\phi )$ 落在一个边长为 $2^{-N+1}$ 的正方体 $Q$ 中.

第三步, 正方体 $Q$ 与边界 $\partial \Omega$ 不相交的情况: $Q\subset \mathring{\Omega }$.

此时, 由于 $\phi$ 在 $Q$ 之外恒为 $0$, 从而 $\frac{\partial \phi }{\partial x_i}$ 在 $Q$ 之外也恒为 $0$, 所以, 我们可以把积分限制到 $Q$ 上: $$\begin{array}{r}{\int }_{\Omega }\frac{\partial \phi }{\partial x_i}dx={\int }_Q\frac{\partial \phi }{\partial x_i}dx,\end{array}$$其中, $dx=d{x}_1\cdots d{x}_n$. 我们不妨假设 $Q=I_1\times I_2\times \cdots \times I_n$, 其中, $I_i=[a_i,b_i]$. 所以, 根据 Fubini 公式和 Newton-Leibniz 公式, 我们得到$$\begin{array}{rl}{\int }_Q\frac{\partial \phi }{\partial x_i}dx& ={\int }_{I_1\times \cdots \times \widehat{I_i}\times \cdots \times I_n}\left({\int }_{a_i}^{b_i}\frac{\partial \phi }{\partial x_i}d{x}_i\right)d{x}_1\cdots \widehat{d{x}_i}\cdots d{x}_n\\ & ={\int }_{I_1\times \cdots \times \widehat{I_i}\times \cdots \times I_n}\phi (x_1,\cdots ,b_i,\cdots ,x_n)-\phi (x_1,\cdots ,a_i,\cdots ,x_n)d{x}_1\cdots \widehat{d{x}_i}\cdots d{x}_n.\end{array}$$上面表达式中, 一个符号上面加上 $\hat{}$ 表示这个符号不在那里. 由于 $\phi$ 的支集在 $Q$ 中, 所以$$\phi (x_1,\cdots ,b_i,\cdots ,x_n)=\phi (x_1,\cdots ,b_i,\cdots ,x_n)=0.$$从而上面的积分为 $0$. 另外, 由于 $\frac{\partial \phi }{\partial x_i}$ 在 $\partial \Omega$ 上为 $0$, 所以此时 Stokes 公式成立.

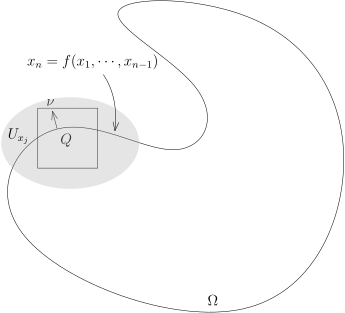
第四步, 正方体 $Q$ 与边界 $\partial \Omega$ 相交的情况: $Q\cap \mathring{\Omega }\ne \varnothing$, 此时, 我们可以假设 $Q\subset U_{x_j}$, 其中, $U_{x_j}$ 是第一步中构造的开集.

由于 $\partial \Omega \cap U_{x_j}$ 为函数的图像, 我们不妨假设$$\partial \Omega \cap U_{x_j}=\{(x_1,\cdots ,x_{n-1},x_n)|x_n=f(x_1,\cdots ,x_{n-1})\}.$$我们还假设 $\Omega$ 是函数图像下的部分, 即 $x_n⩽f(x_1,\cdots ,x_{n-1})$. 我们定义$$\rho (x_1,\cdots ,x_n)=f(x_1,\cdots ,x_{n-1})-x_n.$$并且选取函数光滑递增的单变量实函数 $\theta (x)$: $$\theta (x)=\{\begin{array}{ll}1,& x⩾1;\\ 0,& x⩽-1.\end{array}$$(函数的存在性请参考上个学期作业七习题 F) 我们知道, 当 $\epsilon \to 0$ 时, 我们有函数的逐点收敛: $$\theta \left(\frac{\rho (x)}{\epsilon }\right)⟶1_{\Omega \cap Q}.$$根据 Lebesgue 控制收敛定理, 我们有$$\begin{array}{rl}{\int }_{\Omega }-\frac{\partial \phi }{\partial x_i}(x)dx& ={\int }_Q-\frac{\partial \phi }{\partial x_i}(x)dx\\ & \stackrel{Lebesgue}{=}\underset{\epsilon \to 0}{\lim }{\int }_Q-\frac{\partial \phi }{\partial x_i}(x)\theta \left(\frac{\rho (x)}{\epsilon }\right)dx\\ & =\underset{\epsilon \to 0}{\lim }{\int }_Q\frac{1}{\epsilon }{\theta }^{\prime }\left(\frac{\rho (x)}{\epsilon }\right)\frac{\partial \rho }{\partial x_i}(x)\phi (x)dx.\end{array}$$最后一个等号我们利用 Fubini 公式可以对 $x_i$ 变量进行分部积分, 这和第三步中的计算一模一样.

为了可以利用 Newton-Leibniz 公式, 我们构造一个微分同胚 (坐标变换) 把 $\Omega \cap Q$ 变成矩形. 我们变量替换$$H:\Omega \cap Q\to {\mathbb{R}}_{-}^n=\{(y_1\cdots ,y_n)|y_n⩽0\},\left(\begin{array}{c}{x}_1\\ \cdots \\ x_{n-1}\\ x_n\end{array}\right)\mapsto \left(\begin{array}{c}{y}_1\\ \cdots \\ y_{n-1}\\ y_n\end{array}\right)=\left(\begin{array}{c}{x}_1\\ \cdots \\ x_{n-1}\\ x_n-f(x_1,\cdots ,x_{n-1})\end{array}\right).$$显然, 我们有 ${\mathbf{J}}_H\equiv 1$, 利用换元积分公式, 我们有$$\begin{array}{rl}{\int }_{\Omega }-\frac{\partial \phi }{\partial x_i}(x)dx& =\underset{\epsilon \to 0}{\lim }{\int }_Q\frac{1}{\epsilon }{\theta }^{\prime }\left(\frac{y_n}{\epsilon }\right)\left(\frac{\partial \rho }{\partial x_i}\right)(H^{-1}(y))\phi (H^{-1}(y))dy\\ & \stackrel{Fubini}{=}\underset{\epsilon \to 0}{\lim }{\int }_{I_1\times \cdots \times I_{n-1}}\left({\int }_{I_n}\frac{1}{\epsilon }{\theta }^{\prime }\left(\frac{y_n}{\epsilon }\right)\left(\frac{\partial \rho }{\partial x_i}\right)(H^{-1}(y))\phi (H^{-1}(y))d{y}_n\right)d{y}_1\cdots d{y}_{n-1}.\end{array}$$蓝色项具有特殊的形式. 注意到 ${\theta }^{\prime }(y_n)$ 这个函数的积分为 $1$, 所以, 根据我们证明的第二个技术性引理 (Dirac $\delta$-函数) , 我们就有$$\begin{array}{rl}& \underset{\epsilon \to 0}{\lim }{\int }_{I_n}\frac{1}{\epsilon }{\theta }^{\prime }\left(\frac{y_n}{\epsilon }\right)\left(\frac{\partial \rho }{\partial x_i}\right)(H^{-1}(y))\phi (H^{-1}(y))d{y}_n\\ & =\left(\frac{\partial \rho }{\partial x_i}\right)(H^{-1}(y_1,\cdots ,y_{n-1},0))\phi (H^{-1}(y_1,\cdots ,y_{n-1},0)).\end{array}$$我们注意到, $y_n=0$ 实际上就是超曲面 $\partial \Omega$. 为了书写简单, 我们令 $Q^{\prime }=I_1\times \cdots \times I_{n-1}$, $x^{\prime }=(x_1,\cdots ,x_{n1})$. 所以, 根据 Lebesgue 控制收敛定义 (交换积分和极限) , 我们有$$\begin{array}{rl}{\int }_{\Omega }-\frac{\partial \phi }{\partial x_i}(x)dx& ={\int }_{Q^{\prime }}\left(\frac{\partial \rho }{\partial x_i}\right)(H^{-1}(y_1,\cdots ,y_{n-1},0))\phi (H^{-1}(y_1,\cdots ,y_{n-1},0))d{y}_1\cdots d{y}_{n-1}\\ & ={\int }_{Q^{\prime }}\left(\frac{\partial \rho }{\partial x_i}\right)(x_1,\cdots ,x_{n-1},x_n){|}_{\rho =0}\phi (x_1,\cdots ,x_n){|}_{\rho =0}d{x}_1\cdots d{x}_{n-1}\\ & ={\int }_{Q^{\prime }}\left(\frac{\partial \rho }{\partial x_i}\right)(x^{\prime },x_n){|}_{\partial \Omega }\phi (x^{\prime },f(x^{\prime }))d{x}^{\prime }\\ & ={\int }_{Q^{\prime }}\frac{1}{\sqrt{1+|\nabla f(x^{\prime }){|}^2}}\left(\frac{\partial \rho }{\partial x_i}\right)(x^{\prime },x_n){|}_{\partial \Omega }\phi (x^{\prime },f(x^{\prime }))\sqrt{1+|\nabla f(x^{\prime }){|}^2}d{x}^{\prime }.\end{array}$$我们注意到, $\phi (x^{\prime },f(x^{\prime }))\sqrt{1+|\nabla f(x^{\prime }){|}^2}d{x}^{\prime }$ 就是 $\partial \Omega$ 的曲面测度 $d\sigma$. 另外, 根据之前的计算, $$\nu =\frac{1}{(1+|\nabla f{|}^2{)}^{\frac{1}{2}}}(-\nabla f,1),$$所以, $$\frac{1}{\sqrt{1+|\nabla f(x^{\prime }){|}^2}}\left(\frac{\partial \rho }{\partial x_i}\right)(x^{\prime },x_n){|}_{\partial \Omega }=-{\nu }_i.$$上式就可以写成$$\begin{array}{rl}{\int }_{\Omega }-\frac{\partial \phi }{\partial x_i}(x)dx& ={\int }_{\partial \Omega }-{\nu }_i\phi d\sigma .\end{array}$$这就对这种情况证明了 Stokes 公式, 从而命题得证.

$\square$

注记. 上述证明的一个和核心想法是把函数 $\phi$ 拆成支集很小的函数的和来进行证明而不是把 $\Omega$ 拆成更小的集合! 也就是说, 把 $\Omega$ 分成小块是更直观的看法, 但是为了实现这个想法, 我们应该走到函数的层次上.