导数计算的补充 先证明上次课堂上没有证明的一个重要推论:
I J R f : I → J f − 1 : J → I f f ′ ( x 0 ) = 0 f − 1 x 0 ( f − 1 ) ′ ( f ( x 0 )) = f ′ ( x 0 ) 1 .
证明. 实际上, 只要证明 f − 1 y 0 = f ( x 0 ) f − 1 f ∘ f − 1
我们不妨假设
f 是严格递增的 (因为
f 连续并且可逆, 根据介值定理,
f 是单调的) , 那么
f − 1 是连续的. 特别地, 在
J 中, 当
y → y 0 时, 我们有
f − 1 ( y ) → f − 1 ( y 0 ) . 根据介值定理, 当
y 从左边到右边遍历
[ − ε + y 0 , y 0 + ε ] 时, 令
x = f − 1 ( y ) , 从而
x 也恰好从左边到右边遍历了区间
[ x 0 − δ 1 , x 0 + δ 2 ] , 其中
x 0 − δ 1 = f − 1 ( y 0 − ε ) ,
x 0 + δ 2 = f − 1 ( y 0 + ε ) . 特别地, 在这个区间里面,
x → x 0 等价于 y → y 0 . 所以,
y → y 0 lim y − y 0 f − 1 ( y ) − f − 1 ( y 0 ) = y → y 0 lim ( f − 1 ( y ) − f − 1 ( y 0 ) y − y 0 ) − 1 = y → y 0 lim ( x − x 0 f ( x ) − f ( x 0 ) ) − 1 = x → x 0 lim ( x − x 0 f ( x ) − f ( x 0 ) ) − 1 . 上式最后一个不起眼的等号是证明的核心, 我们把
y → y 0 的信息转化为
x → x 0 的信息. 根据极限的四则运算法则, 这个极限显然存在. 特别地, 上述的证明直接给出了反函数求导的公式.
我们给出两个著名的公式:
假设 f g R n ( f ⋅ g ) ( n ) ( x ) = k = 0 ∑ n ( k n ) f ( k ) ( x ) g ( n − k ) ( x ) .
证明. 我们对
n 进行归纳. 当
n = 1 时, 这就是四则运算法则. 假设对于
n 命题成立, 那么
( f ⋅ g ) ( n + 1 ) = d x d ( f ⋅ g ) ( n ) = ( k = 0 ∑ n ( k n ) f ( k ) ( x ) g ( n − k ) ( x ) ) ′ = k = 0 ∑ n ( k n ) ( f ( k + 1 ) ( x ) g ( n − k ) ( x ) + f ( k ) ( x ) g ( n − k + 1 ) ( x ) ) = k = 0 ∑ n + 1 ( ( k − 1 n ) + ( k n ) ) f ( k ) ( x ) g ( n + 1 − k ) ( x ) = k = 0 ∑ n + 1 ( k n + 1 ) f ( k ) ( x ) g ( n + 1 − k ) ( x ) 最后一步我们利用了组合数的基本性质: 从
n + 1 个数中选取
k 个数的方式有两种可能, 如果第
n + 1 个数在这
k 个数中出现, 那么剩下的
k − 1 个数要在前
n 个数中选取, 一共有
( k − 1 n ) 种选取方式; 如果第
n + 1 个数不在这
k 个数中出现, 那么这
k 个数要在前
n 个数中选取, 一共有
( k n ) 种选取方式.
我们对于复合函数的
n 次导数也有公式:
( f ∘ g ) ( n ) ( x ) = m = 1 ∑ n ( k 1 , ⋯ , k n ) ∈ Γ m , n ∑ k 1 ! k 2 ! ⋯ k n ! n ! f ( m ) ( g ( x )) ( 1 ! g ( 1 ) ( x ) ) k 1 ( 2 ! g ( 2 ) ( x ) ) k 2 ⋯ ( n ! g ( n ) ( x ) ) k n , Γ m , n Γ m , n = { ( k 1 , ⋯ , k n ) ∣ ∣ k 1 , ⋯ , k n ∈ Z ⩾ 0 , k 1 + k 2 + ⋯ + k n = m , k 1 + 2 k 2 + ⋯ + n k n = n } .
为了对上面的公式有个直观的认识, 这次的作业里有对
n = 2 或
3 的验证, 这是练习链式法则的好例子. 由于命题证明的实质是组合数学而和分析学没有更进一步的联系, 我们略去, 请感兴趣的同学查阅互联网或者其他书籍.
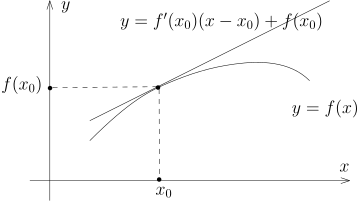
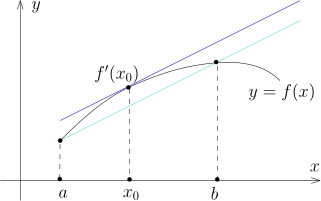
导数的直观意义与微分 用导数来研究函数的性质是数学分析中的重要课题, 在学习这一部分知识之前, 我们重新来审视一下导数的 “直观意义”:
首先, 导数的精确定义是通过公式 f ( x 0 ) = x → x 0 lim x − x 0 f ( x ) − f ( x 0 )
1)
几何的看法, 即把导数解释为函数图像的斜率.
2)
物理的若干看法: f ( t ) f
下面强调的是逼近的 解释, 我们说过这是分析学中贯穿始终的看问题的方法.
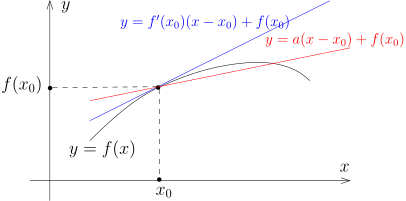
假设 f x 0 线性 映射: ℓ : R → R , h ↦ f ′ ( x 0 ) h , ℓ ( h ) = f ′ ( x 0 ) h δ ( h ) = f ( x 0 + h ) − f ( x 0 ) − f ′ ( x 0 ) h = ( f ( x 0 + h ) − f ( x 0 ) ) − ℓ ( h ) h → 0 lim h δ ( h ) = 0 h → 0 δ ( h ) = o ( 1 ) h f ( x ) − f ( x 0 ) = ℓ ( x − x 0 ) + o ( 1 ) ( x − x 0 ) , x → x 0 . o ( 1 ) ( x − x 0 ) x − x 0 x → x 0 ℓ ( x − x 0 ) f ( x ) − f ( x 0 ) f ( x ) x − x 0 ℓ ( x − x 0 ) + f ( x 0 ) x 0 f f
考虑另外线性映射 ℓ ′ ( h ) = ah ℓ ′ = ℓ f ′ ( x 0 ) = a ℓ ℓ ′ x 0 x − x 0 f ( x ) − f ( x 0 ) f ( x ) − f ( x 0 ) − ℓ ( x − x 0 ) = f ( x ) − f ( x 0 ) − ℓ ′ ( x − x 0 ) = E 1 ( h ) , 第一个误差 o ( 1 ) h , E 2 ( h ) , 第二个误差 ( f ′ ( x 0 ) − a ) h + o ( 1 ) h . h = x − x 0 h → 0 lim E 1 ( h ) E 2 ( h ) = h → 0 lim o ( 1 ) h ( f ′ ( x 0 ) − a ) h + o ( 1 ) h = ∞.
作为总结, 我们有
如果要用一个线性映射 L : R → R L ( x − x 0 ) x 0 f ( x ) − f ( x 0 ) h ↦ f ′ ( x 0 ) h 观点上的重要转变 , 如果用df ( x 0 ) : R → R , h ↦ f ′ ( x 0 ) h , df ( x 0 ) df ( x 0 ) : R → R f ′ ( x 0 ) df ( x 0 ) R T x 0 R df ( x 0 ) R T f ( x 0 ) R df ( x 0 ) : T x 0 R → T f ( x 0 ) R , h ↦ f ′ ( x 0 ) h .
当我们研究高维甚至是无限维空间 (定义域和值域都可以是任意的) 的时候, 这个新的观点 (用线性映射在一点附近来逼近一个映射) 有着非常自然的推广. 从这个观点来看, 我们将要研究的偏导数和微分之间的关系也会更明朗.
我们把上述定义的 df ( x 0 ) : T x 0 R → T f ( x 0 ) R f x 0 微分 .
在进一步探究可微函数更为精细的结构之前, 如果对比收敛和连续性部分内容, 我们很自然会问是否可以将导数的概念推广到其他的空间 (值域) ? 比如说, f : R → C f : R → R N f ( x 0 ) = x → x 0 lim x − x 0 f ( x ) − f ( x 0 ) . f : R → V 值域 V
所以, 只要 V V V
假设 ( V , ∥ ⋅ ∥ ) I ⊂ R f : R → V x 0 ∈ I x → x 0 lim x − x 0 f ( x ) − f ( x 0 ) f x 0 可导 并记此时 f ′ ( x 0 ) = x → x 0 lim x − x 0 f ( x ) − f ( x 0 ) f ′ ( x 0 ) ∈ V V
考虑 V = R n V ∥ ⋅ ∥ 2 f : R → R n , x ↦ f ( x ) = ( f 1 ( x ) , ⋯ , f n ( x )) . f x 0 f k x 0 f ′ ( x ) = ( f 1 ′ ( x ) , ⋯ , f n ′ ( x ) ) . sin x cos x e i x z ↦ i z C
另外, 我们可以按定义来计算 e i x
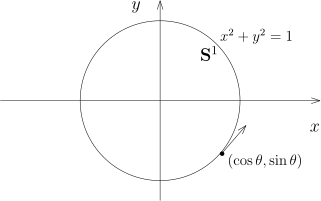
我们定义映射E : R → C = R 2 , θ ↦ ( cos θ , sin θ ) . S 1 = { ( x , y ) ∈ R 2 ∣ ∣ x 2 + y 2 = 1 } . R 2 ∥ ⋅ ∥ 2 1 单位圆 .
试证明
E ( R ) = S 1 (即单位圆上的每个点都可以写成
( sin θ , cos θ ) 的形式, 这不是显然的) . 对任意的
θ ∈ R , 试计算
E ′ ( θ ) (这一般被视为是单位圆在一点处的切向量) . 这是本次作业的一道题目, 是非常有意义的练习.
可微函数的性质 导数是局部定义的, 我们用导数研究函数的局部性质:
I ⊂ R f : I → R x 0 f ′ ( x 0 ) = 0 f ′ ( x 0 ) > 0 x 0 U = ( x 0 − ε , x 0 + ε )
1)
对任意的 x ∈ U x > x 0 f ( x ) > f ( x 0 )
2)
对任意的 x ∈ U x < x 0 f ( x ) < f ( x 0 )
如果假设 f ′ ( x 0 ) < 0
证明. 根据微分以及极限的定义, 由于
f ′ ( x 0 ) > 0 , 所以对于
δ = 2 1 f ′ ( x 0 ) , 存在
ε > 0 , 使得对任意
∣ x − x 0 ∣ < ε , 即
x ∈ U = ( x 0 − ε , x 0 + ε ) , 我们有
∣ ∣ x − x 0 f ( x ) − f ( x 0 ) − f ′ ( x 0 ) ∣ ∣ < 2 1 f ′ ( x 0 ) ⇒ x − x 0 f ( x ) − f ( x 0 ) > 2 1 f ′ ( x 0 ) > 0. 所以
f ( x ) − f ( x 0 ) 与
x − x 0 同号, 从而命题得证.
在所谓的临界情形, f ′ ( x 0 ) ⩾ 0 f x 0 f ( x 0 )
I ⊂ R f : I → R I x ∈ I f ′ ( x ) > 0 f I
在所谓的临界情形, f ′ ( x 0 ) ⩾ 0 f x 0 f ( x 0 ) x ∈ I f ′ ( x ) ⩾ 0 f I
另外, 即使 f ′ ( x 0 ) > 0 x 0 U = ( x 0 − ε , x 0 + ε ) f U
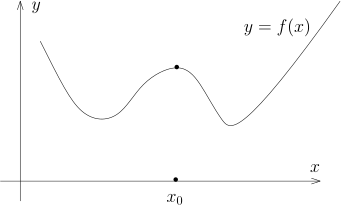
上面引理有一个重要的推论 (然而简单) , 它可以帮助我们寻找函数的最大最小值 (在非数学领域中, 这个定理是可能被应用的最多的, 比如说经济学和工程里) . 为此, 我们引入局部极大值和局部极小值的概念. 假设 f : I → R I ⊂ R x 0 ∈ I x 0 U ⊂ I f ( x 0 ) f U x 0 f 局部极大值 ; 类似地, 我们可以定义局部极小值 . x 0 f f x 0
假设 f I f x 0 ∈ I f ′ ( x 0 ) = 0 f ( x ) f ′ ( x )
证明. 如若不然, 不妨假设
f ′ ( x 0 ) > 0 , 那么
f 在
x 0 右边的附近的点的取值比
f ( x 0 ) 要大, 所以,
x 0 就不可能是局部极大值, 矛盾.
利用这个定理, 证明两个出名的定理 (在这两个定理之上有一大类有意思或者困难的习题, 然而这两个定理是一元微分学中的结果, 在高维空间没有特别有意义的推广) :
假设实值函数 f ∈ C ([ a , b ]) ( a , b ) f ( a ) = f ( b ) x 0 ∈ ( a , b ) f ′ ( x 0 ) = 0
证明. 如果
f 是常值函数, 那么不证自明. 如果
f 不是常值函数, 不妨设有
x 1 ∈ ( a , b ) , 使得
f ( x 1 ) > f ( a ) = f ( b ) . 由于连续函数在闭区间上有最大值, 我们假设
x 0 是
f ( x ) 的最大值. 所以,
f ( x 0 ) ⩾ f ( x 1 ) > f ( a ) = f ( b ) , 这表明
x 0 ∈ ( a , b ) . 另外,
x 0 自然是局部极大的, 所以
f ′ ( x 0 ) = 0 .
Rolle 中值定理对向量值的函数不成立, 比如说, 我们考虑 (先假设 π 2 π sin x cos x E : [ 0 , 2 π ] → R 2 , x ↦ ( cos x , sin x ) . E ( 0 ) = E ( 2 π ) x ∈ [ 2 , 2 π ] E ′ ( x ) = 0
假设实值函数 f ∈ C ([ a , b ]) ( a , b ) x 0 ∈ ( a , b ) f ′ ( x 0 ) = b − a f ( b ) − f ( a )
最容易记住这个定理的方式就是搞明白下面的图讲了什么样的几何意义:
证明. 考虑函数
g ( x ) = f ( x ) − b − a f ( b ) − f ( a ) ( x − a ) . 我们知道,
g ( a ) = g ( b ) 都等于
f ( a ) , 所以可以用 Rolle 中值定理, 存在
x 0 ∈ ( a , b ) , 使得
g ′ ( x 0 ) = 0 ⇔ f ′ ( x 0 ) − b − a f ( b ) − f ( a ) = 0. 命题得证.
我们证明 1 维版本的反函数定理 (由于 R 1 R n R 1 连续可微 和可微 这两个概念之间的细微 (巨大) 差别.
I ⊂ R f ∈ C 1 ( I ; R ) f ′ ( x 0 ) = 0 f x 0 C 1 -同胚 , 即存在 x 0 ( − ε + x 0 , x 0 + ε ) f ( x 0 ) ( f ( x 0 ) − δ 1 , f ( x 0 ) + δ 2 ) f ( − ε + x 0 , x 0 + ε ) f ∣ ∣ ( − ε + x 0 , x 0 + ε ) : ( − ε + x 0 , x 0 + ε ) ⟶ f ( − ε + x 0 , x 0 + ε ) = ( f ( x 0 ) − δ 1 , f ( x 0 ) + δ 2 ) f − 1 : ( f ( x 0 ) − δ 1 , f ( x 0 ) + δ 2 ) ⟶ ( − ε + x 0 , x 0 + ε )
证明. 不妨假设
f ′ ( x 0 ) > 0 . 由于
f ′ 连续, 所以存在
x 0 的邻域
U = ( − ε + x 0 , x 0 + ε ) , 使得
f ′ 在
U 上的取值都是正的 (这里用到了
f ′ 的连续性! ) . 所以,
f 是
U 上严格递增的函数. 在本次课的一开始关于关于反函数导数的结论中, 我们证明了
f : U → f ( U ) 是双射 (去掉端点) 并且
f − 1 : f ( U ) → U 是可微的. 剩下只要说明
f − 1 是连续可微的即可, 这因为
( f − 1 ) ′ ( y ) = f ′ ( f − 1 ( y )) 1 是连续函数的复合.
在上述的定理中, 如果我们进一步要求 f f ∈ C ∞ ( I ) f − 1
证明. 定理已经说明
f − 1 是可微的并且
( f − 1 ) ′ ( y ) = f ′ ( f − 1 ( y )) 1 . 根据可微函数的复合仍然可微, 所以
( f − 1 ) ′ 还可微的并且可以计算它的导数:
( ( f − 1 ) ′ ) ′ ( y ) = − ( f ′ ( f − 1 ( y )) ) 2 ( f − 1 ) ′ ( y ) f ′′ ( f − 1 ( y )) . 据此,
f − 1 的二次导数也可微. 我们可用归纳的方式继续求导, 值得注意的是分母上只有
f ′ ( f − 1 ( y )) 出现, 它永远不会是零.
反函数定理是一个纲领性的定理, 凡是用到了微积分的课程它总会出现. 定理的本意是如何正确地参数化一个几何对象, 由于在一维空间上的结构简单, 问题的解决可以依赖于一维空间的特殊性, 所以我们体会可能不深. 反函数定理在高维空间的情形会以最自然最朴素的方式登场.
另外, 这个定理已经包含了所谓的椭圆正则性 (偏微分方程中的黑话) 的雏形: 定理告诉我们, 只要知道是 C 1
处处不可微的连续函数 如果 f R f R f R f ( x ) = k = 1 ∑ ∞ a k cos ( b k π x ) .
我们要求 a ∈ ( 0 , 1 ) b ∈ Z ⩾ 1 ab > M 0 M 0
首先, 对任意固定的 N > 0 C ([ − N , N ]) C ([ − N , N ]) ∥ g ∥ ∞ = x ∈ [ − N , N ] sup ∣ g ( x ) ∣ k = 1 ∑ ∞ ∥ a k cos ( b k π x ) ∥ ∞ ⩽ k = 1 ∑ ∞ a k < ∞ , f ( x ) ∈ C ([ − N , N ]) N → ∞ f ( x ) ∈ C ( R ) f R
为了说明 f a k cos ( b k π x ) b k ( ab ) k π
任意固定 y 0 ∈ R f y 0 { y n } n ⩾ q y n → y 0 y n → y 0 lim y n − y 0 f ( y n ) − f ( y 0 )
首先, 对任意的正整数 n z n b n y 0 − z n ∈ [ 0.1 , 1.1 ) y n = b n z n y n → y 0
其次, 我们将要计算的极限拆为两项: y n − y 0 f ( y n ) − f ( y 0 ) = k = 1 ∑ ∞ a k y n − y 0 cos ( b k π y n ) − cos ( b k π y 0 ) = S 1 k = 1 ∑ n − 1 ( ab ) k b k ( y n − y 0 ) cos ( b k π y n ) − cos ( b k π y 0 ) + S 2 k = 0 ∑ ∞ a n + k y n − y 0 cos ( b n + k π y n ) − cos ( b n + k π y 0 ) S 1 ∣ S 1 ∣ ⩽ k = 1 ∑ n − 1 ( ab ) k ∣ ∣ b k ( y n − y 0 ) cos ( b k π y n ) − cos ( b k π y 0 ) ∣ ∣ ⩽ k = 1 ∑ n − 1 ( ab ) k π ∣ cos ( θ k ) ∣ ⩽ k = 1 ∑ n − 1 π ( ab ) k ⩽ π ab − 1 ( ab ) n . S 2 z k b y n cos ( b n + k π y n ) = cos ( b k π z n ) = ( − 1 ) z n . ϑ k = b k y 0 − z k ∈ [ 0.1 , 1.1 ) cos ( b n + k π y 0 ) = cos ( b n y 0 ⋅ b k π ) = cos ( b k π z n + b k π ϑ n ) = ( − 1 ) z n cos ( b k π ϑ n ) . y n − y 0 = − b n ϑ n S 2 = k = 0 ∑ ∞ ( − 1 ) z n a n + k y n − y 0 1 − cos ( b k π ϑ n ) = k = 0 ∑ ∞ ( − 1 ) z n + 1 ( ab ) n a k ϑ n 1 − cos ( b k π ϑ n ) = ( − 1 ) z n + 1 ( ab ) n k = 0 ∑ ∞ a k ϑ n 1 − cos ( b k π ϑ n ) . ϑ n > 0 ϑ k ∣ ∣ k = 0 ∑ ∞ a k ϑ n 1 − cos ( b k π ϑ n ) ∣ ∣ = k = 0 ∑ ∞ a k ϑ n 1 − cos ( b k π ϑ n ) ⩾ ϑ n 1 − cos ( π ϑ n ) ,
根据 ϑ n ∈ [ 0.1 , 1.1 ) 1 − cos ( π ϑ n ) ⩾ δ 0 δ 0 ϑ n ⩽ 1.1 ∣ ∣ k = 0 ∑ ∞ a k ϑ n 1 − cos ( b k π ϑ n ) ∣ ∣ ⩾ 1. 1 − 1 δ 0 ≥ 10 δ 0 . ∣ S 2 ∣ ⩾ 10 δ 0 ( ab ) n . ∣ S 1 + S 2 ∣ ⩾ ∣ S 2 ∣ − ∣ S 1 ∣ ⩾ ( ab ) n ( 10 δ 0 − ab − 1 π ) .
为了要求 S 1 + S 2 ab > δ 0 10 π + 1 = M 0 . n → ∞ y n → y 0 lim y n − y 0 f ( y n ) − f ( y 0 ) = + ∞