34. 隐函数定理, 子流形的判定

隐函数定理

我们假设 $\Omega \subset {\mathbb{R}}^{n+p}$ 是开集. 为了定理的叙述方便, 我们将 ${\mathbb{R}}^{n+p}$ 写成乘积结构 ${\mathbb{R}}^n\times {\mathbb{R}}^p$. 在 ${\mathbb{R}}^n$ 上面我们用坐标 $x=(x_1,\cdots ,x_n)$, 在 ${\mathbb{R}}^p$ 上面我们用坐标 $y=(y_1,\cdots ,y_p)$. 对于 $\Omega$ 上的映射／函数 $f$, 我们用 $f(x,y)$ 这样的二元函数来表示, 其中 $x\in {\mathbb{R}}^n$, $y\in {\mathbb{R}}^p$. 为了行文方便, 我们引入下面 (不标准的) 符号: 将 $y$ 固定, 我们就可以将 $f(x,y)$ 看作是 $x$ 的函数, 即$$f(\cdot ,y):{\mathbb{R}}^n\to {\mathbb{R}}^m,$$从而我们可以对 $x$ 的微分, 我们将这个微分记作 $d_{x}f(x,y)$; 类似地, 我们可以定义 $d_{y}f(x,y)$.

我们首先给出隐函数定理的经典叙述 (和证明) , 然后用子流形的语言就可以有更清晰的几何表述.

定理 34.1 (隐函数定理). 给定正整数 $n$ 和 $p$ 和非空开集 $\Omega \subset {\mathbb{R}}^n\times {\mathbb{R}}^p$, 映射 $f:\Omega \to {\mathbb{R}}^p$ 是连续可微的 ($C^1$ 的) .

假设 $(x^{\ast },y^{\ast })\in \Omega$, 使得 $f(x^{\ast },y^{\ast })=0$, 其中 $x^{\ast }\in {\mathbb{R}}^n$, $y^{\ast }\in {\mathbb{R}}^p$, $0\in {\mathbb{R}}^p$. 如果 $\left(d_{y}f\right)(x^{\ast },y^{\ast })$ 是可逆的, 即 Jacobi 矩阵 $(\frac{\partial f_i}{\partial y_j}{)}_{1⩽i,j⩽p}$ 在 $(x^{\ast },y^{\ast })$ 点是可逆的. 那么, 存在开集 $U\subset {\mathbb{R}}^n$, $x^{\ast }\in U$, 存在开集 $V\subset {\mathbb{R}}^p$, $y^{\ast }\in V$, 存在连续可微的映射 $\varphi :U\to V$, 使得对任意的点 $(x,y)\in \Omega$, 如下两条是等价的:

•	$(x,y)\in U\times V$ 并且 $f(x,y)=0$;
•	$x\in U$ 并且 $y=\varphi (x)$.

我们进一步还有 $d\varphi (x)=-(d_{y}f(x,y){)}^{-1}\circ d_{x}f(x,y)$.

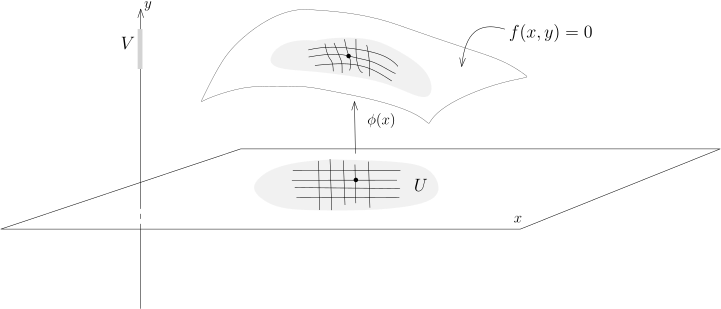
注记. " 隐 " 函数说的是方程 $f(x,y)=0$ 实际上隐含地将 $y$ 定义成 $x$ 的函数, 定理具体地将这个函数构造了出来: $y=\varphi (x)$. 当 $p=1$ 时, $f(x,y)=0$ 在空间中所定义的曲面局部上就可以表达成 $y=\varphi (x)$ 的形式, 也就是说它局部上可以看成是函数的图像, 从而是 ${\mathbb{R}}^{n+1}$ 中余 1 维的子流形, 下面的图很好的总结了这个情形:

例子. 隐函数定理的叙述乍看起来晦涩难懂. 最简单的就是如下的情形: $\Omega ={\mathbb{R}}^n\times {\mathbb{R}}^p$, $f$ 是投影映射: $$f:{\mathbb{R}}^n\times {\mathbb{R}}^p\to {\mathbb{R}}^p,(x_1,\cdots ,x_n,y_1,\cdots ,y_p)\mapsto (y_1,\cdots ,y_p).$$此时, $U={\mathbb{R}}^n$, $V={\mathbb{R}}^p$ 而$$\varphi :{\mathbb{R}}^n\to {\mathbb{R}}^p,x\mapsto 0.$$这显然满足定理的要求, 因为 $f(x,y)=0\iff y=0$. 隐函数定理本质上说只要选取适当的坐标系这是唯一的例子.

证明. 我们利用反函数定理来证明隐函数定理. 为此, 我们通过把 $f$ 的值域空间加一些维数来定义一个新的映射. 注意到, 对于 $x\in {\mathbb{R}}^n$, $f(x,y)\in {\mathbb{R}}^p$ (如果 $(x,y)$ 落在 $f$ 的定义域里的话) . 所以, 以下的映射是良好定义的: $$F:\Omega \to {\mathbb{R}}^n\times {\mathbb{R}}^p,(x,y)\mapsto F(x,y)=(x,f(x,y)).$$很明显, $F$ 是连续可微的 (因为它的每个分量都是连续可微的) . 我们可以计算 $F$ 在 $(x,y)$ 处微分, 用 Jacobi 矩阵来显然可以表达成: $$dF=\left(\begin{array}{cc}\mathrm{id}& 0\\ d_{x}f& d_{y}f\end{array}\right),$$(34.1)这是一个 $(n+p)\times (n+p)$ 的方阵. 由于 $(d_{y}f)(x^{\ast },y^{\ast })$ 可逆, 所以分块矩阵 $(dF)(x^{\ast },y^{\ast })$ 也是可逆的. 所以, 我们可以对映射 $F$ 在 $(x^{\ast },y^{\ast })$ 处用反函数定理: 存在开集 $\tilde{U}\subset \Omega$, $(x^{\ast },y^{\ast })\in \tilde{U}$, 存在开集 $\tilde{V}\subset {\mathbb{R}}^{n+p}$ 并且通过将它缩小我们可以假设它具有乘积结构 $\tilde{V}=\widetilde{V_1}\times \widetilde{V_2}$ 以及连续可微的映射 $G:\tilde{V}\to \tilde{U}$ (这是 $F$ 的逆) , 使得$$G\circ F={\mathrm{id}}_{\tilde{U}},F\circ G={\mathrm{id}}_{\tilde{V}}.$$我们可以参考下面的示意图:

我们将 $F$ 的值域 (即 $G$ 的定义域) 上的坐标用 $(x^{\prime },y^{\prime })$ 来表示. 按照分量的记法, 可以将 $G$ 写成$$G(x^{\prime },y^{\prime })=(\stackrel{\in {\mathbb{R}}^n}{\overbrace{G_1(x^{\prime },y^{\prime })}},\stackrel{\in {\mathbb{R}}^p}{\overbrace{G_2(x^{\prime },y^{\prime })}}).$$我们把反函数定理给出的两个等式用分量写出来, 就有$$\begin{array}{rl}G\circ F={\mathrm{id}}_{\tilde{U}}& \Rightarrow G_1(x,f(x,y))=x,G_2(x,f(x,y))=y;\\ F\circ G={\mathrm{id}}_{\tilde{V}}& \Rightarrow G_1(x^{\prime },y^{\prime })=x^{\prime },f(x^{\prime },G_2(x^{\prime },y^{\prime }))=y^{\prime }.\end{array}$$总结一下, 我们得到了$$\{\begin{array}{ll}& G(x^{\prime },y^{\prime })=(x^{\prime },G_2(x^{\prime },y^{\prime })),\\ & G_2(x,f(x,y))=y,\\ & f(x^{\prime },G_2(x^{\prime },y^{\prime }))=y^{\prime }.\end{array}$$按照 $F$ 和 $G$ 的定义, 对于给定的 $(x,y)\in \tilde{U}$, 我们有如下的等价关系$$f(x,y)=0\iff F(x,y)=(x,0)\iff (x,y)=F^{-1}(x,0)=G(x,0)=(x,G_2(x,0)).$$所以, 如果我们令 $\varphi (x)=G_2(x,0):V\to {\mathbb{R}}^p$, 那么, 给定的 $(x,y)\in \tilde{U}$, 我们有如下的等价关系$$f(x,y)=0\iff y=\varphi (x).$$所以, 我们可以取 $U=\tilde{U}$, $V=\widetilde{V_1}$, 这就证明了隐函数定理的主要论述.

最终, 为了计算微分, 我们对 $f(x,\varphi (x))=0$ 求微分, 即对映射$$U\to {\mathbb{R}}^p,x\mapsto f(x,\varphi (x))$$求微分. 我们得到$$d{f}_x(x,y)+d{f}_y(x,y)\cdot d\varphi (x)=0,\text{其中}y=\varphi (x).$$在 $(x^{\ast },y^{\ast })$ 的附近, $d{f}_y(x,y)$ 是可逆的, 所以 $d\varphi (x)=-(d_{y}f(x,y){)}^{-1}\circ d_{x}f(x,y)$.

$\square$

注记. 如果我们把反函数定理条件中映射改为 $C^{\infty }$ 的, 那么结论中的函数和映射也是 $C^{\infty }$, 这从反函数定理的叙述就可以看出来.

隐函数定理的子流形叙述

利用子流形这个概念, 我们可以更形象地理解隐函数定理. 反过来, 隐函数定理给出了一种非常实用的判断子流形的方法.

假设 $M\subset {\mathbb{R}}^N$ 是一个 $d$-维的子流形, 所以对任意的 $x\in M$, 存在开集 $U\subset {\mathbb{R}}^N$ 包含 $x$, ${\mathbb{R}}^n$ 中的开集 $V$ 以及微分同胚 $\phi :U\to V$ 使得$$\phi :U\cap M=V\cap ({\mathbb{R}}^d\times \{0\}),$$

我们现在沿用隐函数定理中的符号. 我们令$$M=\{(x,y)\in {\mathbb{R}}^n\times {\mathbb{R}}^p|f(x,y)=0\}.$$由于 $f(x,y)=0$ 实际上是 $p$ 个方程 (以为 $f:{\mathbb{R}}^{n+p}\to {\mathbb{R}}^p$) , 所以, 我们将上述集合是 ${\mathbb{R}}^{n+p}$ 中由 $p$ 个方程的零点集合. 如果 $f$ 的某些导数为非退化的 (参考隐函数定理的叙述) , 那么局部上这个 $M$ 可以表达成映射的图像的形式, 即对任意的 $(x,y)\in M$, 局部上都等价于 $y=\varphi (x)$. 从另外一种观点来看, $M$ 可以被 $x$ 参数化, 即给定 $x$, 就唯一地确定了 $M$ 上的一个点.

为了说明 $M$ 实际上是微分子流形, 我们需要构造一个映射 $\Phi :{\mathbb{R}}^{n+p}\to {\mathbb{R}}^{n+p}$, 使得 $\phi$ 是微分同胚 (局部上) 并且将 $M$ 映射成右边 ${\mathbb{R}}^{n+p}$ 上的由 $y_1=\cdots =y_p=0$ 所给出来的线性子空间. 这个映射就是定理证明中的 $F$: $$F(x,y)=(x,f(x,y))=(x,0),\text{其中}(x,y)\in M.$$这样, 我们就证明了 $M$ 实际上 (局部上) 是一个微分子流形.

我们把上面的讨论总结为如下的定理:

定理 34.2 (隐函数: 子流形版本). 给定正整数 $n^{\prime }$ 和 $p$ ($n=n^{\prime }+p$) 和非空开集 $\Omega \subset {\mathbb{R}}^{n^{\prime }+p}={\mathbb{R}}^n$, 映射 $f:\Omega \to {\mathbb{R}}^p$ 是光滑的. 令$$M=\{(x,y)\in {\mathbb{R}}^n\times {\mathbb{R}}^p|f(x,y)=0\}.$$假设 $(x^{\ast },y^{\ast })\in M$ 使得 Jacobi 矩阵 $(\frac{\partial f_i}{\partial y_j}{)}_{1⩽i,j⩽p}$ 在 $(x^{\ast },y^{\ast })$ 点是可逆的. 那么, 存在开集 $U\subset {\mathbb{R}}^n$ 使得 $U\cap M$ 是 ${\mathbb{R}}^n$ 中的 $n^{\prime }$ 维子流形.

这个版本有如下重要的推论:

推论 34.3 (子流形的判断准则). 假设 $f:\Omega \to {\mathbb{R}}^p$ 是光滑映射, 其中 $\Omega \subset {\mathbb{R}}^n$ 是开集, $n⩾p$. 对于 $c\in {\mathbb{R}}^p$, 我们把 $c$ 上纤维定义为的 $c$ 在 $f$ 下的逆像: $$f^{-1}(c)=\{x\in {\mathbb{R}}^{n+p}|f(x)=c\}.$$如果对任意的 $x\in f^{-1}(c)$, $\mathrm{Rank}df(x)=p$. 那么, 纤维 $f^{-1}(c)$ 是余维数为 $p$ 的子流形.

证明. 我们要在 ${\mathbb{R}}^n$ 上的选取坐标系 $x_1,\cdots ,x_n$. 根据 $\mathrm{Rank}df(x)=p$, 通过调整 $x_1,\cdots ,x_n$ 的标号, 我们可以使得后面 $p$ 个坐标 $x_{n-p+1},\cdots ,x_n$ 满足$$(\frac{\partial f_i}{\partial x_{n+1-j}}{)}_{1⩽i,j⩽p}(x)\ne 0,$$其中 $x$ 是任意选定的 $x\in f^{-c}$ 上的点. 我们选取函数 $f-c$ 并且将后 $p$ 个坐标用 $y_1,\cdots ,y_p$ 来表示, 这就化成了隐函数定理的情况. 特别地, 纤维 $f^{-c}$ 在任意一点附近都是 $p$ 维子流形, 所以 $f^{-1}(c)$ 是 $p$-维子流形.

$\square$

注记. 我们注意到定理本身的叙述不需要任何的坐标系, 而证明本身很好地解释了不依赖于坐标和选取坐标系之间的关系.

我们应该和线性代数的情况做类比: 给定 $n$ 维线性空间上的 $p$ 个齐次线性方程, 它们的公共零点是 $n-p$ 的线性子空间当且仅当这 $p$ 个线性方程的秩是 $p$.

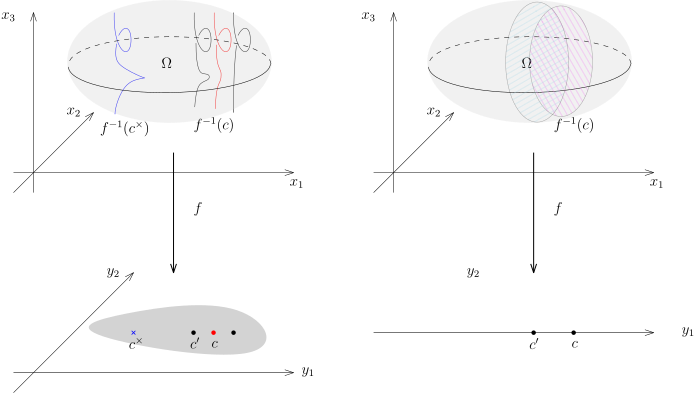
注记 (几何图像). 我们可以用下图形象地记忆并表示这个命题, 这是关于隐函数定理最干净最形象的表述:

左图代表是余维数为 $2$ 的情形. 我们假设 $f:\Omega \to f(\Omega )$, 其中 $f(\Omega )$ 是下面灰色的区域. 对于每个 $c\in \Omega$, 我们可以把它的原像想象成插在这个点上面的一个纤维. 特别地, $\Omega$ 可以被写成这些纤维的无交并: $$\Omega =\coprod _{c\in f(\Omega )}{f}^{-1}(c).$$然而, 我们需要在每个 $x\in f^{-1}(c)$ 点处要求一个非退化的条件才能保证 $f^{-1}(c)$ 是光滑的子流形. 上面的图形表示, 在 $c$ 的纤维如果满足这个非退化的条件, 那么它附近的 $c^{\prime }$ 处的纤维 $f^{-1}(c)$ 也是光滑的子流形: 实际上, 我们需要对 $f^{-1}(c)$ 限制才可以 (比如纤维是紧的) , 但是很多情况下这一点都成立, 大概的原因是 $\mathrm{Rank}df(x)=p$ 如果成立, 就在附近的一个开集上面成立. 然而, 离着 $c$ 比较远的点, 这个条件就可能退化, 比如说上面的蓝色 $c^{\times }$ 点, 它的纤维就 “打折” 了.

左图代表是余维数为 $1$ 的情形, 对于每个 $c$, 我们形象的认为纤维是 $\Omega$ 的一个 “切片”. 事实上, 为了研究高维子流形的结构, 我们经常通过这种切片化成低维数子流形的情况来研究. 在后面的课程和作业中, 我们会用这个方法研究几个重要的例子.

下面的命题是隐函数定理几何版本的逆命题: 子流形总是可以 (在局部上) 由 $\mathrm{codim}M=n-\dim M$ 个方程的零点来定义. 我们已经在第四次课的开始证明了这个结论, 为了完备起见 (也为了再次复习子流形的定义) , 我们概述一下证明.

命题 34.4. 假设 $M^d\subset {\mathbb{R}}^n$ 是 $d$ 维的子流形. 那么, 对任意的 $p\in M$, 存在开集 $U\subset {\mathbb{R}}^n$, $p\in U$ 和 $n-d$ 个光滑函数 $f_1,\cdots ,f_{n-d}\in C^{\infty }(U)$, 使得$$M^d=\{x\in U|f_1(x)=\cdots =f_{n-d}(x)=0\}.$$特别地, 映射的微分$$f:U\to {\mathbb{R}}^{n-d},x\mapsto (f_1(x),\cdots ,f_{n-d}(d))$$在每个点 $x\in M$ 处的秩都是 $n-d$.

证明. 按子流形的定义, 存在开集 $U\subset {\mathbb{R}}^n$ 包含 $p$, ${\mathbb{R}}^n$ 中的开集 $V$ 以及微分同胚 $\phi :U\to V$, 使得$$\phi :U\cap M=V\cap ({\mathbb{R}}^d\times \{0\}).$$我们用 $y_1,\cdots ,y_n$ 表示 $V$ 上的坐标函数, 那么我们选取 $f_i={\phi }^{\ast }{y}_i=y_i\circ \phi$ 即可, 其中 $i=d+1,\cdots ,n$.

$\square$

注记. 我们沿用命题中的记号, 如果令$$M^{d+k}=\{x\in U|f_1(x)=\cdots =f_{n-d-k}(x)=0\},$$那么, $M^{d+k}$ 是 $d+k$ 维的子流形 (作业中会证明) . 换句话说, 每次加上一个 $f_j(x)=0$ 的限制, 子流形的维数恰好降低 $1$ 维.

我们现在给出隐函数定理的几个应用, 首先是用来判定子流形, 现在我们只需要做一些简单的代数计算即可:

1)

${\mathbb{R}}^n$ 中的球面 ${\mathbf{S}}^{n-1}=\{x\in {\mathbb{R}}^n|x_1^2+\cdots +x_n^2=1\}$ 是一个 $n-1$ 维的子流形. 球面可以被视作是函数$$f(x_1,\cdots ,x_n)=(x_1{)}^2+(x_2{)}^2+\cdots +(x_n{)}^2-1$$的零点集. 所以, 只要验证它的微分 $df(x)$ 的秩为 $1$ 即可. 然而, 用矩阵来写$$\begin{array}{rl}df(x)& =\left(\frac{\partial f}{\partial x_1}(x),\cdots ,\frac{\partial f}{\partial x_n}(x)\right)\\ & =2(x_1,\cdots ,x_n).\end{array}$$由于在 ${\mathbf{S}}^{n-1}$ 上, $|x|=1$, 上面的向量显然非零, 所以这是光滑子流形. 这比之前我们把球面 ${\mathbf{S}}^2$ 拆成六块 (参见第三课讲义) 并且将每块写成函数的图像要方便很多.

2)

我们考虑 ${\mathbb{R}}^4={\mathbb{C}}^2$ 中的曲面$${\mathbf{T}}^2=\{(z_1,z_2)||z_1|=1,|z_2|=1\}.$$如果我们用 $(x,y,z,w)$ 作为坐标, 那么这个曲面实际上是$$f(x,y,z,w)=x^2+y^2-1,g(x,y,z,w)=z^2+w^2-1$$这两个方程的公共零点集. 我们需要计算$${\mathbb{R}}^4\to {\mathbb{R}}^2,(x,y,z,w)\mapsto (f(x,y,z,w),g(x,y,z,w)),$$的 Jacobi 矩阵并判断它的秩. 这个矩阵显然是$$\left(\begin{array}{cccc}2x& 2y& 0& 0\\ 0& 0& 2z& 2w\end{array}\right).$$由于在 ${\mathbf{T}}^2$ 上面, $x^2+y^2=1$, $z^2+w^2=1$, 所以上面这个矩阵的秩是 $2$, 从而 ${\mathbf{T}}^2$ 是 $2$ 维的子流形. 它实际上是一个环面 (甜甜圈) :

${\mathbb{R}}^3$ 中由方程定义的曲线和曲面

在经典的微积分课程中, ${\mathbb{R}}^3$ 中由一个方程或者两个方程定义的曲线和曲面是最基本的几何对象. 我们首先引入如下的定义:

定义 34.5. 假设 $M\subset {\mathbb{R}}^n$ 是子流形. 如果 $\dim M=1$, 我们就称之为 ${\mathbb{R}}^n$ 中的一条光滑曲线; 如果 $\dim M=2$, 我们就称之为 ${\mathbb{R}}^n$ 中的一个光滑曲面; 如果 $\dim M=n-1$, 我们就称之为 ${\mathbb{R}}^n$ 中的一个光滑超曲面.

注记. 这里曲线的概念和上个学期所讲的曲线略有不同: 之前是所谓的参数化曲线, 即曲线是一个映射 $\gamma :I\to {\mathbb{R}}^n$, 其中 $I\subset \mathbb{R}$ 是一个区间. 这里的曲线只是 ${\mathbb{R}}^n$ 中的一个子集, 然而根据隐函数定理的结论, 我们在局部上可以给它一个参数化.

我们关心的是如下的对象, 他们有着更特殊的要求:

引理 34.6. 假设 $f:{\mathbb{R}}^n\to \mathbb{R}$ 是光滑函数, 如果对于任意的 $x_0\in f^{-1}(0)$, $df(x_0)\ne 0$, 那么 $f^{-1}(0)$ 是超曲面. 我们把这种超曲面称为由一个方程整体定义的光滑超曲面.

我们把 (显然的) 证明留作作业. 特别地, 在 ${\mathbb{R}}^3$ 中, 我们有

引理 34.7. 假设 $f(x,y,z)$ 是 ${\mathbb{R}}^3$ 上的光滑函数, 如果对于任意满足 $f(x_0,y_0,z_0)=0$ 的点 $(x_0,y_0,z_0)$, 我们有$$\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}\right)(x_0,y_0,z_0)\ne 0,$$那么$$\{(x,y,z)\in {\mathbb{R}}^3|f(x,y,z)=0\}$$是光滑曲面. 我们把这种超曲面称为由一个方程整体定义的光滑曲面.

例子. ${\mathbb{R}}^3$ 中的柱面由如下方程$$x^2+y^2=1$$定义, 这是一个光滑曲面: 我们取 $f(x,y,z)=x^2+y^2-1$, 此时, $$\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}\right)=(2x,2y,0)\ne 0,$$

我们还有用两个方程定义的曲线:

引理 34.8. 假设 $f(x,y,z)$ 和 $g(x,y,z)$ 是 ${\mathbb{R}}^3$ 上的光滑函数, 如果对于任意同时满足 $f(x_0,y_0,z_0)=0$ 和 $g(x_0,y_0,z_0)=0$ 的点 $(x_0,y_0,z_0)$, 如果如下两个向量线性不相关: $$\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}\right)(x_0,y_0,z_0),\left(\frac{\partial g}{\partial x},\frac{\partial g}{\partial y},\frac{\partial g}{\partial z}\right)(x_0,y_0,z_0),$$那么$$\{(x,y,z)\in {\mathbb{R}}^3|f(x,y,z)=0,g(x,y,z)=0\}$$是光滑曲线. 我们把这种曲线称为由两个方程整体定义的光滑曲线.

我们把 (显然的) 证明留作作业.

在结束关于隐函数定理的几何讨论之前, 我们给出隐函数定理的一个对偶版本. 这个版本本身和隐函数是无关的, 之所以是对偶的, 是因为隐函数定理研究从 ${\mathbb{R}}^n$ 到 ${\mathbb{R}}^p$ 的映射, 其中 $n⩾p$, 其结论说映射的逆项或者纤维是子流形. 而这个定理 (证明非常简单, 只要验证定义) 研究从 ${\mathbb{R}}^n$ 到 ${\mathbb{R}}^{p^{\prime }}$ 的映射, 其中 $n⩽p$, 其结论说映射的像是子流形.

定理 34.9 (参数化子流形). $\Omega \subset {\mathbb{R}}^n$ 是开集, $f:\Omega \to {\mathbb{R}}^{n+p}$ 是光滑映射. 假设对于点 $x^{\ast }\in \Omega$, 有 $\mathrm{rank}df(x^{\ast })=n$, 那么, 存在开集 $U\subset {\mathbb{R}}^n$, $x^{\ast }\in U$, 使得 $f(U)\subset {\mathbb{R}}^{n+p}$ 是 $n$ 维的子流形.

证明. 在 $\Omega$ 上选取坐标系统 $x_1,\cdots ,x_n$, 在 ${\mathbb{R}}^{n+p}$ 上选取坐标坐标系统 $y_1,\cdots ,y_n,z_1,\cdots ,z_p$. 我们把 $f$ 用坐标分量写成$$f(x)=(f_1(x),\cdots ,f_{n+p}(x)),$$其中每个 $f_i(x)$ 都是 $\Omega$ 上的光滑函数. 由于有 $\mathrm{rank}df(x^{\ast })=n$, 通过调换 $\{x_i\}$ 坐标的指标, 我们不妨假设$$\det {\left(\frac{\partial f_i}{\partial x_j}\right)}_{i,j⩽n}(x^{\ast })\ne 0.$$我们现在考虑 $F={\pi }_y\circ f$, 其中 $\pi :{\mathbb{R}}^{n+p}\to {\mathbb{R}}^n$ 是取前 $n$ 个坐标, 即换句话说, 我们定义了 $F(x)=(f_1(x),f_2(x),\cdots ,f_n(x))$. 根据上述行列式非零的条件, $F$ 为局部微分同胚 (反函数定理) . 令 $U$ 为 $x$ 在 $\Omega$ 中的开集, $F:V\to F(U)$ 为这个微分同胚并令 $V=F(U)$. 此时, 我们考察 $f(U)\subset {\mathbb{R}}^{n+p}$. 对于 $x\in U$, 令 $y=F(x)$, $f(x)\in {\mathbb{R}}^{n+1}$ 可以写成$$\begin{array}{rl}(f_1(x),\cdots ,f_n(x);f_{n+1}(x),\cdots ,f_{n+p}(x))& =(y;f_{n+1}(x),\cdots ,f_{n+p}(x))\\ & =(y,f_{n+1}(F^{-1}(y),f_{n+2}(F^{-1}(y)),\cdots ,f_{n+p}(F^{-1}(y)).\end{array}$$所以, 它可以被视作是 $V$ 上定义的向量值函数 $y\mapsto f_{n+1}(F^{-1}(y),f_{n+2}(F^{-1}(y)),\cdots ,f_{n+p}(F^{-1}(y))$ 的图像, 这是一个用 $y$ 做为坐标来参数化的子流形 (在本次作业中证明) .

$\square$

在 ${\mathbb{R}}^3$ 还有一个经典曲面: $\mathcal{M}$öbius 带. 我们用参数的方式可以把它写作$$\mathcal{M}=\left\{(x,y,z)\in {\mathbb{R}}^3|\{\begin{array}{ll}& x=(1+r\cos \frac{\theta }{2})\cos \theta ,\\ & y=(1+r\cos \frac{\theta }{2})\sin \theta ,\\ & z=r\sin \frac{\theta }{2}\end{array}\theta \in [0,2\pi ],r\in (-1,1)\right\}.$$适当改变一下书写方式更有启发: $$(x,y,z)=(\cos \theta ,\sin \theta ,0)+(r\cos \frac{\theta }{2}\cos \theta ,r\cos \frac{\theta }{2}\sin \theta ,r\sin \frac{\theta }{2}).$$当 $r=0$ 时, 我们得到一个用 $\theta$ 来参数化的基本圆周 $(\cos \theta ,\sin \theta ,0)$. 给定 $\theta$, 就给定了这个圆周上的一个点 $(\cos \theta ,\sin \theta ,0)$. 固定这个 $\theta$, 当 $r$ 在 $(-1,1)$ 之间变化的时候, 我们就在这个点插上了一个小线段并且这个线段的方向的变化是 $\theta$ 的一半. 所以, 当 $\theta$ 从 $0$ 变化到 $2\pi$, 基本圆周上的点旅行了一周又回到了原来的点, 但是它上面所插的小线段只转动了 $180^{\circ }$.

我们下面证明一个不明显的命题, 为此, 我们先选择好的记号: 把 $r=0$ 光滑圆周写成参数形式: $$\gamma :[0,2\pi ]\to {\mathbb{R}}^3,\theta \mapsto (\cos \theta ,\sin \theta ,0).$$给定 $\theta$ 处, 我们用 $e_0$ 表示 $\gamma$ 在 $\gamma (\theta )$ 处的切方向 ${\gamma }^{\prime }(\theta )$, 即令 $e_0=(-\sin \theta ,\cos \theta ,0)$. 和 $e_0$ 垂直的方向有两个, 我们分别记作$$e_1(\theta )=(\cos \theta ,\sin \theta ,0),e_2(\theta )=(0,0,1).$$据此, 我们把 $M$ 的参数化写成: $$\mathcal{M}=\left\{(x,y,z)=(\cos \theta ,\sin \theta ,0)+r\cos \frac{\theta }{2}{e}_1(\theta )+r\sin \frac{\theta }{2}{e}_2(\theta ),\theta \in [0,2\pi ],r\in (-1,1)\right\}.$$根据刚刚证明的定理, 这是 ${\mathbb{R}}^3$ 中的一个光滑曲面 (参见本次作业) .

命题 34.10. 不存在光滑函数 $f\in C^{\infty }({\mathbb{R}}^3)$, 使得$$\mathcal{M}=\{(x,y,z)|f(x,y,z)=0\}$$且 $df(x,y,z)$ 在 $\mathcal{M}$ 上的每点处不为零, 即 $\mathcal{M}$ 不能只用一个方程零点来整体定义.

注记. 我们需要运用关于由一个方程定义的光滑曲面的特殊性质 (基于连续函数的介值定理) : 给定 $f\in C^{\infty }({\mathbb{R}}^3)$, 假设对任意的 $x\in \Omega$, $df(x)\ne 0$, $f^{-1}(0)\subset \Omega$ 是光滑子流形并且由一个方程定义. 任意选定 $x\in \Omega$, 考虑 $x$ 处的邻域 $U$ (足够小) . 由于 $df(x)\ne 0$, 我们不妨选 $v\in {\mathbb{R}}^n$, 使得$${\nabla }_{v}f(x)=df(x)(v)>0.$$从而, 在当 $\epsilon >0$ 足够小时, $p_{\pm }=x\pm \epsilon v\in U$ 并且 $f(p_{+})>0$, $f(p_{-})<0$. 我们声明, 任何一条连接 $p_{+}$ 和 $p_{-}$ 的曲线都要经过 $f^{-1}(0)$, 即对任意的连续映射 $\gamma :[0,1]\to X$, 其中起点 $\gamma (0)=p_{-}$ 和终点 $\gamma (1)=p_{+}$) , 一定存在 $t_0\in (0,1)$, 使得 $\gamma (t_0)\in f^{-1}(0)$ (等价于说 $f(\gamma (t_0))=0$) . 实际上, $f(\gamma (t))$ 为连续函数, 按照 $p_{\pm }$ 的选取方式, 我们有$$f(\gamma (0))=f(p_{-})<0,f(\gamma (1))=f(p_{+})>0,$$所以连续函数的介值定理就给出了 $t_0$.

我们现在证明关于 Möbius 带的命题:

证明. 我们给出证明的梗概, 证明的细节留给同学们在作业中完成. 如若不然, 假设 $f$ 是 $\mathcal{M}$ 的定义方程. 任选 $p=(\cos \theta ,\sin \theta ,0)\in \mathcal{M}$, 直观上 (实际上也是) 这个附近的小邻域 $U$ 被 $f$ 的图像分成了两个部分: 在一部分中, $f>0$; 在另一部分中, $f<0$. 我们选取在 $p$ 点处和整个曲面垂直的法向量$$\nu (\theta )=\cos \frac{\theta }{2}{e}_2(\theta )-\sin \frac{\theta }{2}{e}_1(\theta )$$我们考虑曲线$$\beta :[0,2\pi ]\to {\mathbb{R}}^3,(\cos \theta ,\sin \theta ,0)+\epsilon \nu (\theta ).$$我们可以适当的选取比较小的 $\epsilon$ (可正可负) , 使得 $f(\beta (0))>0$. 然而, $\gamma (2\pi )=\gamma (0)$, 曲线所对应的 $\epsilon$ 却变换了符号, 从而, $f(\beta (2\pi ))<0$. 很明显, 这条曲线与曲面 $\mathcal{M}$ 不相交, 矛盾.

$\square$