37. Hesse 矩阵与极值点, 凸函数

Hesse 矩阵与极值点的二阶导数判定

为了避免张量的概念, 我们考虑 ${\mathbb{R}}^n$ 中的开集 $\Omega$ 并假设 ${\mathbb{R}}^n$ 中已经选取坐标 $(x_1,\cdots ,x_n)$. 我们假设 $f$ 是 $\Omega$ 上至少两次连续可微的函数. 对于给定的点 $p\in \Omega$, 我们定义 $f$ 在 $p$ 处的 Hesse 矩阵为$${\nabla }^{2}f(p)=H_f(p)=\left(\frac{{\partial }^{2}f}{\partial x_i\partial x_j}(p)\right)=\left(\begin{array}{cccc}\frac{{\partial }^{2}f}{\partial x_1^2}(p)& \frac{{\partial }^{2}f}{\partial x_1\partial x_2}(p)& \cdots & \frac{{\partial }^{2}f}{\partial x_1\partial x_n}(p)\\ \frac{{\partial }^{2}f}{\partial x_2\partial x_1}(p)& \frac{{\partial }^{2}f}{\partial x_1^2}(p)& \cdot & \frac{{\partial }^{2}f}{\partial x_2\partial x_n}(p)\\ \cdots & \cdot & \cdots & \cdots \\ \frac{{\partial }^{2}f}{\partial x_n\partial x_1}(p)& \frac{{\partial }^{2}f}{\partial x_n\partial x_2}(p)& \cdots & \frac{{\partial }^{2}f}{\partial x_n^2}(p)\end{array}\right)$$根据 Clairaut-Schwarz 的定理, 这是一个对阵矩阵. 另外, 根据线性代数中所学的知识, 我们还可以将 Hesse 矩阵看成是 ${\mathbb{R}}^2$ 上的二次型: $$H_f(p):{\mathbb{R}}^n\otimes {\mathbb{R}}^n\to \mathbb{R},(v,w)\mapsto \sum _{1⩽i,j⩽n}\frac{{\partial }^{2}f}{\partial x_i\partial x_j}{v}_i{w}_j.$$我们假设在 ${\mathbb{R}}^n$ 给了内积 $⟨\cdot ,\cdot ⟩$, 使得 ${\left\{\frac{\partial }{\partial x_i}\right\}}_{i⩽n}$ 恰好是标准正交基. 那么上面的二次型还可以写成$$H_f(v,w)=⟨v,{\nabla }^{2}f(w)⟩.$$另外, 我们的 Taylor 公式在 $2$ 阶的时候可以写成$$f(x)=f(x_0)+⟨\nabla f(x_0),x-x_0⟩+\frac{1}{2}⟨x-x_0,{\nabla }^{2}f(x_0)(x-x_0)⟩+o(|x-x_0{|}^2).$$

对于实对称矩阵, 我们可以讨论它是否正定／负定. 我们简单回忆线性代数中的概念: 矩阵／二次型 ${\nabla }^{2}f$ 是正定 (半正定) 的, 指的是它满足如下条件之一:

1)	对任意的 $v\in {\mathbb{R}}^n$, $H_f(v,v)>0$ ($H_f(v,v)⩾0$) ;
2)	矩阵 ${\nabla }^{2}f$ 的特征值都是正 (非负) 的.

我们用 ${\nabla }^{2}f>0$ 和 ${\nabla }^{2}f⩾0$ 表示正定和半正定的二次型; 负定的情形类似.

命题 37.1. 给定 $f\in C^2(\Omega )$, 其中 $\Omega \subset {\mathbb{R}}^d$ 是开集, 如果 $x_0\in \Omega$ 是 $f$ 的最小值点, 那么, $\nabla f(x_0)=0$ 并且 ${\nabla }^{2}f(p_0)⩾0$ (半正定) .

证明. 首先, $\nabla f(x_0)=0$ 即 $df(x_0)=0$, 这是明显的. 为了说明 ${\nabla }^{2}f(x_0)⩾0$, 我们用反证法, 假设 ${\nabla }^{2}f$ 有一个负特征值 $\lambda <0$, 我们用 $v$ 表示相应的一个特征向量 (非零) . 考虑 $x=x_0+tv$ 并利用 Taylor 公式 (一阶导数项自动为零) : $$\begin{array}{rl}f(x)& =f(x_0)+\frac{1}{2}⟨tv,{\nabla }^{2}f(x_0)(tv)⟩+o(|x-x_0{|}^2)\\ & =f(x_0)+\lambda \times \frac{|v{|}^2{t}^2}{2}+o(t^2|v{|}^2)\end{array}$$根据 $o(|t{|}^2)$ 的定义, 存在 $\epsilon >0$, 当 $|t|<\epsilon$ 时, 我们有 $o(t^2|v{|}^2)<\frac{1}{2}|\lambda |\frac{|v{|}^2{t}^2}{2}$. 根据 $\lambda <0$, 从而$$\begin{array}{r}f(x)<f(x_0)+\lambda \times \frac{|v{|}^2{t}^2}{4}<f(x_0)\end{array}$$这与 $x_0$ 是最小值矛盾.

$\square$

这个证明可以用来证明一个接近于上述命题逆命题的命题:

命题 37.2. 给定 $f\in C^2(\Omega )$, 其中 $\Omega \subset {\mathbb{R}}^d$ 是开集, 如果 $x_0\in \Omega$ 满足 $\nabla f(x_0)=0$ 并且 ${\nabla }^{2}f(p_0)>0$ (正定) , 那么, $x_0$ 是 $f$ 的局部最小值点, 即存在开集 $U\subset \Omega$, 使得 $x_0$ 是 $f$ 在 $\Omega$ 上的最小值.

证明. 由于 ${\nabla }^{2}f(p_0)>0$, 我们令 $0<{\lambda }_1⩽{\lambda }_2⩽\cdots ⩽{\lambda }_n$ 是它的特征值, 其中 ${\lambda }_1$ 是最小的特征向量. 根据线性代数的知识, 我们可以选取相应于上述特征值的特征向量 $v_1,v_2,\cdots ,v_n$, 其中它们都是单位向量并且两两正交. 据此, 对任意的 $w\in {\mathbb{R}}^n$, 我们可以把 $x$ 写成$$w=a_1{v}_1+\cdots +a_n{v}_n,\sqrt{\sum _{i⩽n}(a_i{)}^2}=|x|.$$由于 ${\nabla }^{2}f(x_0)(w)={\lambda }_1{a}_1{v}_1+\cdots +{\lambda }_n{a}_n{v}_n$, 所以, 我们有$$|{\nabla }^{2}f(x_0)(w)|=\sqrt{\sum _{i⩽n}({\lambda }_i{a}_i{)}^2}⩾{\lambda }_1|w|.$$根据 Taylor 公式 (一阶导数项自动为零) , 我们有$$\begin{array}{rl}f(x)& =f(x_0)+\frac{1}{2}⟨x-x_0,{\nabla }^{2}f(x_0)(x-x_0)⟩+o(|x-x_0{|}^2)\\ & ⩾f(x_0)+{\lambda }_1|x-x_0{|}^2+o(|x-x_0{|}^2)\end{array}$$根据 $o(|x-x_0{|}^2)$ 的定义, 存在 $\epsilon >0$, 当 $|x-x_0|<\epsilon$ 时 (我们就选取 $U=B_{\epsilon }(x_0)$) , 我们有 $o(|x-x_0{|}^2)<\frac{1}{2}|\lambda |\frac{|x-x_0{|}^2}{2}$. 从而$$\begin{array}{r}f(x)>f(x_0)+\lambda \times \frac{|x-x_0{|}^2}{4}>f(x_0)\end{array}$$这说明 $x_0$ 是 $U$ 中的最小值点.

$\square$

二阶导数与凸函数

给定凸集 $\Omega \subset {\mathbb{R}}^n$ (即对任意的 $x,y\in \Omega$, 对任意的 $t\in [0,1]$, $tx+(1-t)y\in \Omega$) , $f:\Omega \to \mathbb{R}$ 是在凸集上定义的函数, 如果对任意的 $x,y\in \Omega$, 对任意的 $t\in [0,1]$, 都有$$f(tx+(1-t)y)⩽tf(x)+(1-t)f(y).$$我们就称 $f$ 是凸函数. (如果 $-f$ 是凸函数, 就称 $f$ 是凹函数)

另外, 如果对任意的 $x,y\in \Omega$, 对任意的 $t\in (0,1)$, 都有$$f(tx+(1-t)y)<tf(x)+(1-t)f(y).$$我们就称 $f$ 是严格凸的.

换而言之, 对于任意 $\Omega$ 中的线段, $f$ 在这个线段上的限制是 $1$ 维的凸函数. 另外, 我们可以同样地证明 Jensen 不等式 (请参见上学期第十八次课, 证明完全可以照搬) :

命题 37.3 (Jensen 不等式). 假设 $f:\Omega \to \mathbb{R}$ 是凸函数, 其中 $\Omega \subset {\mathbb{R}}^n$ 为凸集, 那么对任意的 $x_1,\cdots ,x_n\in \Omega$ 和任意的 $t_1,\cdots ,t_n\in [0,1]$, 其中 $t_1+t_2+\cdots +t_n=1$, 我们有$$f(t_1{x}_1+\cdots +t_n{x}_n)⩽t_{1}f(x_1)+\cdots +t_{n}f(x_n).$$

例子. 我们先看几个凸函数的例子 (我们总假设 $\Omega \subset {\mathbb{R}}^n$ 是凸集)

1)	$f(x)=a_1{x}_1+\cdots +a_n{x}_n+b$ 是 $\Omega$ 上的线性函数.
2)	假设 $\Vert \cdot \Vert :{\mathbb{R}}^n\to \mathbb{R}$ 是任意一个范数, 那么, 这是一个凸函数, 因为$$\Vert tx+(1-t)y\Vert ⩽\Vert tx\Vert +\Vert (1-t)y\Vert =t\Vert x\Vert +(1-t)\Vert y\Vert .$$
3)	假设 $A$ 是一个 $n\times n$ 的半正定矩阵, 那么, 二次型$$f(x)=⟨x,Ax⟩$$是凸函数. 实际上, 我们可以验证代数恒等式: $$(1-t)f(x)+tf(y)-f((1-t)x+ty)=t(1-t)f(x-y).$$右边的值是非负的.

定理 37.4 (凸函数在开集上的连续性). 假设 $\Omega \subset {\mathbb{R}}^n$ 是凸的开集, $f:\Omega \to \mathbb{R}$ 是凸函数, 那么, $f$ 是连续函数.

证明. 假设 $0\in \Omega$, 我们只要证明 $f$ 在 $0$ 处连续即可, 其余的点类似. 我们不妨假设如下的向量$$\pm e_1=(\pm 1,0,\cdots ,0),\cdots ,\pm e_n=(0,\cdots ,0,\pm 1)$$都在 $\Omega$ 中 (否则做适当的放缩即可, 或者选取 $\epsilon \pm e_i$ 来代替这些向量) . 我们注意到, 当 $r$ 足够小的时, 任意的 $|x|<r$, 如果 $x$ 在第一相限 (即坐标都是非负的) , 存在 ${\lambda }_1,\cdots ,{\lambda }_n\in [0,1)$ 使得$$x={\lambda }_1{e}_1+{\lambda }_2{e}_2+\cdots +{\lambda }_n{e}_n.$$如果 $r$ 足够小, 我们还可以要求 ${\lambda }_1+\cdots +{\lambda }_n<1$, 这是因为$${\lambda }_1+\cdots +{\lambda }_n⩽\sqrt{n({\lambda }_1^2+\cdots +{\lambda }_n^2)}=|x|\sqrt{n}.$$选定这样一个 $r$. 此时, 我们令 ${\lambda }_0=1-{\lambda }_1\cdots -{\lambda }_n$, 所以$$x={\lambda }_0\cdot 0+{\lambda }_1{e}_1+{\lambda }_2{e}_2+\cdots +{\lambda }_n{e}_n.$$根据凸函数的性质 (Jensen 不等式) , 我们就有$$\begin{array}{rl}f(x)& ⩽{\lambda }_{0}f(0)+{\lambda }_{1}f(e_1)+{\lambda }_{2}f(e_2)+\cdots +{\lambda }_{n}f(e_n)\\ & =f(0)+{\lambda }_1\left(f(e_1)-f(0)\right)+\cdots +{\lambda }_n\left(f(e_n)-f(0)\right).\end{array}$$从而, $$\begin{array}{rl}f(x)-f(0)& ⩽{\lambda }_1\left(f(e_1)-f(0)\right)+\cdots +{\lambda }_n\left(f(e_n)-f(0)\right)\\ & ⩽\sqrt{{\lambda }_1^2+\cdots +{\lambda }_n^2}\sqrt{|f(e_1)-f(0){|}^2+\cdots +|f(e_n)-f(0){|}^2}.\end{array}$$即 (对其他相限类似可以证明) $$f(x)-f(0)⩽C|x|,\text{对任意的}|x|<r.$$我们还可以用 $x,-e_1,\cdots ,-e_n$ 的凸组合来表示 $0$, 实际上, 利用 $x$ 的坐标, 我们选取$${\lambda }_0=\frac{1}{x_1+\cdots +x_n+1},{\lambda }_i={\lambda }_0{x}_i,i⩾1.$$此时, 我们有$$0={\lambda }_{0}x+{\lambda }_1(-e_1)+{\lambda }_2(-e_2)+\cdots +{\lambda }_n(-e_n).$$所以, $$\begin{array}{rl}f(0)& ⩽{\lambda }_{0}f(x)+{\lambda }_{1}f(-e_1)+{\lambda }_{2}f(-e_2)+\cdots +{\lambda }_{n}f(-e_n)\\ & ={\lambda }_0\left(f(x)+x_{1}f(-e_1)+x_{1}f(-e_2)+\cdots +x_{n}f(-e_n)\right).\end{array}$$从而, $$\begin{array}{rl}f(0)-f(x)& ⩽({\lambda }_0-1)f(x)+\underset{\text{类似前述},⩽C^{\prime }|x|}{\underbrace{{\lambda }_0\left(x_{1}f(-e_1)+x_{1}f(-e_2)+\cdots +x_{n}f(-e_n)\right)}}.\end{array}$$对于第一项, 我们有$$|({\lambda }_0-1)f(x)|⩽\frac{x_1+\cdots +x_2}{1+x_1+\cdots +x_n}|f(x)|⩽C^{\prime \prime }|x||f(x)|.$$从而, $$\begin{array}{rl}f(0)-f(x)& ⩽C^{\prime \prime }|x||f(x)|+C^{\prime }|x|\\ & ⩽C^{\prime \prime }|x||f(x)-f(0)|+C^{\prime \prime }|x||f(0)|+C^{\prime }|x|.\end{array}$$综合之前的不等式, 我们就得到$$|f(x)-f(0)|⩽C^{\prime \prime }|x||f(x)-f(0)|+C^{\prime \prime \prime \prime }|x|.$$不妨假设选取的 $|x|$ 使得 $C^{\prime \prime }|x|<0.5$, 从而, $$|f(x)-f(0)|⩽2C^{\prime \prime \prime \prime }|x|.$$这就说明了 $f(x)$ 是连续的 (实际上是局部 Lipschitz 的) .

$\square$

如果 $f$ 具有一阶导数的话, 我们可以用几何的方式 (大约是切平面) 来描述凸函数 (请参考上学期第十八次课中凸函数的五个等价定义) :

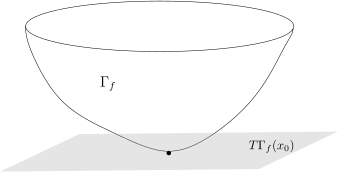
命题 37.5. 假设 $\Omega \subset {\mathbb{R}}^n$ 是凸的开集, $f:\Omega \to \mathbb{R}$ 是可微函数 (即微分 $df$ 逐点存在) , 我们用 ${\Gamma }_f$ 表示 $f$ 在 $\Omega \times \mathbb{R}\subset {\mathbb{R}}^n\times \mathbb{R}$ 中的图像: $${\Gamma }_f=\{(x,y)\in {\mathbb{R}}^n\times \mathbb{R}|x\in \Omega ,y=f(x)\}.$$该图像在 $(x_0,f(x_0))$ 处的切平面我们定义为$$T{\Gamma }_f(x_0)=\{(x_0,f(x_0))+df(x_0)(x-x_0)|x\in {\mathbb{R}}^n\}.$$那么, 如下命题是等价的:

1)	$f$ 是 $\Omega$ 上的凸函数;
2)	对任意的 $x_0\in \Omega$, 函数图像 ${\Gamma }_f$ 都在切平面 $T{\Gamma }_f(x_0)$“上方”, 即$$f(x)⩾L_{x_0}(x),$$其中 $L_{x_0}(x)=f(x_0)+df(x_0)(x-x_0)$, $x\in \Omega$.

证明. 证明分两个方向:

1)	假设 $f$ 是凸函数, 所以对任意的 $x,y\in \Omega$, 函数 $f(tx+(1-t)y)$ 是凸函数并且$$f((1-t)x+ty)⩽(1-t)f(x)+tf(y)=f(x)+t(f(y)-f(x)).$$另外, 根据 Taylor 公式以及可微性, 我们有$$f((1-t)x+ty)=f(x+t(y-x))=f(x)+tdf(x)(y-x)+o(t).$$令 $t\to 0$, 我们就得到$$df(x)(y-x)⩽f(x).$$令 $x=x_0$, $y=x$, 整理就得到 2) 中的等式.
2)	反过来, 我们假设 2) 中不等式成立, 对于给定的 $x,y\in \Omega$, $t\in [0,1]$, 我们令 $z=(1-t)x+ty$. 对 $z$ 用不等式, 我们有$$f(w)⩾f(z)+df(z)(w-z).$$令 $w=x$ 和 $w=y$, 我们得到$$\begin{array}{rl}& f(x)⩾f(z)-tdf(z)(y-x),\\ & f(y)⩾f(z)+(1-t)df(z)(y-x),.\end{array}$$将第一个不等式乘 $(1-t)$, 将第二个不等式乘 $t$, 然后相加就得到所要的结论.

我们还可以将函数限制到线段上用 1 维结论直接说明等价性, 这留给同学思考.

$\square$

如果我们的函数是二阶可微的, 类似于 $1$ 维的情况, 我们也有对凸函数的二阶导数的判定:

命题 37.6. 假设 $\Omega \subset {\mathbb{R}}^n$ 是凸的开集, $f:\Omega \to \mathbb{R}$ 是 $C^2$ 的函数, 那么, $f$ 是凸函数当且仅当 $f$ 在每个点处的 Hesse 矩阵都是半正定的. 进一步, 如果在每个点处 Hesse 矩阵都是正定的, 那么 $f$ 是严格凸的.

证明. 首先假设 $f$ 是凸函数. 我们在 $x_0$ 处将 $f$ 进行 Taylor 展开: $$\begin{array}{rl}f(x)& =\underset{L_{x_0}(x-x_0)}{\underbrace{f(x_0)+⟨\nabla f(x_0),x-x_0⟩}}+\frac{1}{2}⟨x-x_0,{\nabla }^{2}f(x_0)(x-x_0)⟩+o(|x-x_0{|}^2)\\ & ⩾L_{x_0}(x-x_0).\end{array}$$从而, 对任意的 $x\to x_0$, 我们有$$\frac{1}{2}⟨x-x_0,{\nabla }^{2}f(x_0)(x-x_0)⟩+o(|x-x_0{|}^2)⩾0.$$令 $x-x_0=tv$, $t=|x-x_0|$, 其中 $v$ 是任意的长为 $1$ 的向量, 从而$$t^2\frac{1}{2}⟨v,{\nabla }^{2}f(x_0)(v)⟩+o(t^2)⩾0\Rightarrow \frac{1}{2}⟨v,{\nabla }^{2}f(x_0)(v)⟩⩾o(1).$$令 $t\to 0$, 我们就得到了$$⟨v,{\nabla }^{2}f(x_0)(v)⟩⩾0,$$其中 $v$ 是任意的长为 $1$ 的向量, 所以 ${\nabla }^{2}f(x_0)$ 是正定的.

反过来, 我们假设在任何一点 $x_0\in \Omega$ 处, 我们有 ${\nabla }^{2}f(x_0)⩾0$. 此时, 根据 Talyor 展开公式 (Lagrange 余项) , 我们有$$\begin{array}{rl}f(x)-L_{x_0}(x-x_0)& =\frac{1}{2}⟨x-x_0,{\nabla }^{2}f(x^{\prime })(x-x_0)⟩⩾0,\end{array}$$其中 $x^{\prime }$ 位于 $x_0$ 与 $x$ 之间. 根据前面一阶导数的命题, $f$ 是凸的.

$\square$