19. Riemann 和与 Darboux 上下和

我们介绍如何利用经典的 Riemann 和以及 Darboux 上下和的观点来研究 Riemann 可积的函数. 值得强调的是, Riemann 和 (以及上节课用阶梯函数来定义积分的方式) 对于在赋范线性空间中取值的函数可以定义, 然而 Darboux 上下和只对实数值的函数可行 (原因是我们需要用到实数域上的序结构) .

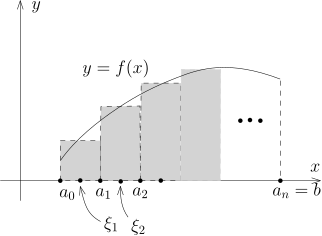
任意给定分划 $σ \in S$ , 假设 $σ = {a = a_{0} < a_{1} < \dots < x_{n} - 1 < a_{n} = b}$ , 我们在每一小段上面选取 $ξ = (ξ_{1}, \dots, ξ_{n})$ , 使得 $ξ_{i} \in [a_{i - 1}, a_{i}]$ . 为了简单起见, 我们用 $ξ$ 表示这些 $ξ_{i}$ , 用 $(σ, ξ)$ 表示给定了分划 $σ$ 并在每一段中选好 $ξ$ . 我们将 $(σ, ξ)$ 的全体记作 $S^{'} = S^{'} (I)$ .

给定函数 $f : I \to R$ 和 $(σ, ξ) \in S^{'}$ , 我们定义所谓的 Riemann 和 $S (f; σ, ξ) = (a_{1} - a_{0}) f (ξ_{1}) + (a_{2} - a_{1}) f (ξ_{2}) + \dots + (a_{n} - a_{n - 1}) f (ξ_{n}) .$

我们证明, 对于 Riemann 可积的函数

f

, 在正确的意思下, 有

∣ σ ∣ \to 0 lim S (f; σ, ξ) = \int_{a}^{b} f .

定理 19.1. 假设 $I \subset R$ 是有界闭区间, $f \in R (I)$ . 对任意的 $ε > 0$ , 存在 $δ > 0$ , 使得对任意的 $(σ, ξ) \in S^{'} (I)$ , 如果其步长 $∣ σ ∣ < δ$ , 那么 $∣ ∣ S (f; σ, ξ) - \int_{a}^{b} f ∣ ∣ < ε .$

证明. 根据 Riemann 可积的定义, 我们选定阶梯函数 $F \in E (I)$ 和 $ψ \in E (I)$ , 使得 $∣ f (x) - F (x) ∣ ⩽ ψ (x)$ 并且 $\int_{a}^{b} ψ (x) < \frac{ε}{4}$ . 我们进一步假设 $F$ 和 $ψ$ 都对应着分划 $σ_{0} = {b_{0} < b_{1} < \dots < b_{m}}$ , 即它们在每一段 $(b_{i}, b_{i + 1})$ 上的限制都是常数.

现在, 任意选取分划 $σ = {a = a_{0} < a_{1} < \dots < a_{n - 1} < a_{n} = b}$ , 我们要求 $∣ σ ∣$ 比 $σ_{0}$ 中最短区间的长度还要小. 利用积分的线性, 我们有 $∣ ∣ S (f; σ, ξ) - \int_{a}^{b} f ∣ ∣ ⩽ i = 1 \sum n ∣ ∣ \int_{a_{i - 1}}^{a_{i}} f (x) - f (ξ_{i}) ∣ ∣$ 我们想逐项地控制上面右端的的每一个积分项 $∣ ∣ \int_{a_{i - 1}}^{a_{i}} f (x) - f (ξ_{i}) ∣ ∣$ . 为此, 我们需要讨论两个分划 $σ_{0}$ 和 $σ$ 之间的相对关系. 对每个 $i$ , 我们有两种情况:

•

情形 1: $[a_{i - 1}, a_{i}]$ 中不包含 $σ_{0}$ 的任何一个分割点 $b_{k}$ .

此时, $ψ$ 和 $F$ 在 $(a_{i - 1}, a_{i})$ 都是常数. 所以, 对任意的 $x \in (a_{i - 1}, a_{i})$ 上, 我们有 $∣ f (x) - f (ξ_{i}) ∣ ⩽ ∣ f (x) - F (x) ∣ + ∣ F (x) - f (ξ_{i}) ∣ = ∣ f (x) - F (x) ∣ + ∣ F (ξ_{i}) - f (ξ_{i}) ∣ ⩽ ψ (x) + ψ (ξ_{i}) = 2∣ ψ (x) ∣.$ 所以, 我们有 $∣ ∣ \int_{a_{i - 1}}^{a_{i}} f (x) - f (ξ_{i}) ∣ ∣ ⩽ 2 \int_{a_{i - 1}}^{a_{i}} ψ .$

•

情形 2: $[a_{i - 1}, a_{i}]$ 中包含某个 $σ_{0}$ 的某一个分割点 $b_{k_{0}}$ . (我们注意到, 由于 $∣ σ ∣$ 比 $σ_{0}$ 中的最短区间的长度还小, 所以 $[a_{i - 1}, a_{i}]$ 恰好只包含 $b_{k_{0}}$ 的这一个 $σ_{0}$ 中的分割点. ) 这样的区间的个数不会超过 $2 m + 1$ 个, 因为 $σ_{0}$ 的分割点一共就 $m + 1$ 个.

此时, 我们用 $∥ f ∥_{\infty}$ 来控制 $f (x)$ , 从而有 $∣ ∣ \int_{a_{i - 1}}^{a_{i}} f (x) - f (ξ_{i}) ∣ ∣ ⩽ ∣ a_{i} - a_{i - 1} ∣∥ f ∥_{\infty} + ∣ a_{i} - a_{i - 1} ∣∣ f (ξ_{i}) ∣ ⩽ 2∣ σ ∣∥ f ∥_{\infty} .$

综合上面的讨论, 当

∣ σ ∣ < ∣ σ_{0} ∣

时, 我们有

∣ ∣ S (f; σ, ξ) - \int_{a}^{b} f ∣ ∣ ⩽ 第一种情况 2 \sum \int_{a_{i - 1}}^{a_{i}} ψ + 第二种情况 2 (2 m + 1) ∣ σ ∣∥ f ∥_{\infty} ⩽ 2 \int_{a}^{b} ψ + 2 (2 m + 1) ∣ σ ∣∥ f ∥_{\infty} ⩽ \frac{1}{2} ε + 2 (2 m + 1) ∣ σ ∣∥ f ∥_{\infty} .

由于

m

是固定的, 当

∣ σ ∣

足够小的时候, 上面的式子明显小于

ε

, 证明完毕.

$□$

注记. 我们们通常将定理写作 $∣ σ ∣ \to 0 lim S (f; σ, ξ) = \int_{a}^{b} f$ , 其中 $f \in R (I)$ . 实际上, 任意选取一个序列 ${(σ_{n}, ξ_{n})}_{n ⩾ 1} \subset S^{'} (I)$ , 上面的定理表明只要当 $∣ σ_{n} ∣ \to 0$ , 我们就有 $lim_{n \to \infty} S (f; σ_{n}, ξ_{n}) = \int_{a}^{b} f$ . 根据这个定理, 我们可以选择方便计算的 Riemann 和来计算积分. 另外, 这个定理还提供了一个很重要的观点用来计算极限: 如果某个极限过程是某个 Riemann 和取极限的话, 那么我们可以利用积分算极限 (当然, 这需要我们有足够好的手段来计算积分) .

下面来定义所谓的上积分和下积分的概念. 假设 $f : I \to R$ 是在 $R$ 中取值的有界函数, 我们要利用 $R$ 中序关系. 定义 $\overline{E_{f}} (I) \underline{E_{f}} (I) = {φ \in E (I) ∣ φ (x) ⩾ f (x)}, = {φ \in E (I) ∣ φ (x) ⩽ f (x)} .$ 由于 $f$ 是有界函数, 所以这两个集合是非空的: 假设对任意的 $x \in I$ , $- M ⩽ f (x) ⩽ M$ , 那么常值函数 $M \in \overline{E_{f}} (I)$ , 常值函数 $- M \in \underline{E_{f}} (I)$ . 据此, 我们定义 $\overline{\int_{a}^{b}} f = φ \in \overline{E_{f}} (I) in f \int_{a}^{b} φ, \underline{\int}_{a}^{b} f = φ \in \underline{E_{f}} (I) sup \int_{a}^{b} φ .$ 由于对任意的 $φ \in \overline{E_{f}} (I)$ , $φ (x) ⩾ - M$ , 所以 $\int_{a}^{b} φ ⩾ - M (b - a)$ , 这说明 $\overline{\int_{a}^{b}} f$ 是良好定义的; 类似地, $\underline{\int}_{a}^{b} f$ 也是良好定义的. 这两个式子分别被称作是有界函数 $f$ 的上积分和下积分. 按照定义, 我们有如下平凡的不等式: $\overline{\int_{a}^{b}} f ⩾ \underline{\int}_{a}^{b} f .$

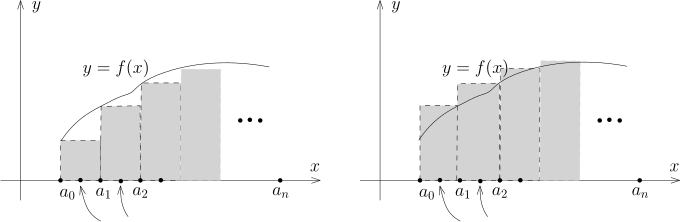
现在引入 Darboux 上下和的概念: 假设 $f : I \to R$ 是有界函数, $σ \in S (I)$ 是一个分划, 其中 $σ = {a = a_{0} < a_{1} < \dots < a_{n - 1} < a_{n} = b}$ . 根据 $f$ 有界, 对每个 $i = 1, 2, \dots, n$ , 我们令 $M_{i} = x \in [a_{i - 1}, a_{i}] sup f (x), m_{i} = x \in [a_{i - 1}, a_{i}] in f f (x),$ 据此, 可以定义 $\overline{S} (f; σ) = i = 1 \sum n (a_{i} - a_{i - 1}) M_{i}, \underline{S} (f; σ) = i = 1 \sum n (a_{i} - a_{i - 1}) m_{i} .$ 我们把这两个和式称作是有界函数 $f$ 对于分划 $σ$ 的 Darboux 上和和 Darboux 下和, 我们可以用下面的示意图来表示:

上图中, 左边代表的是 Darboux 下和, 右边代表的是 Darboux 上和. 很明显, 我们有

\overline{S} (f; σ) ⩾ \underline{S} (f; σ) .

实际上, 我们有更强的结论:

引理 19.2. 对于任意两个分划 $σ, σ^{'} \in S (I)$ , 我们有 $\underline{S} (f; σ) ⩽ \overline{S} (f; σ^{'}) .$

证明. 事实上, 我们只需要证明当

σ ≺ σ^{'}

时, 我们有

\underline{S} (f; σ) ⩽ \overline{S} (f; σ^{'}), \underline{S} (f; σ^{'}) ⩽ \overline{S} (f; σ),

即可. 我们把这个性质的证明留作作业.

$□$

另外, 当

σ ≺ σ^{'}

时, 我们有

\overline{S} (f; σ) ⩽ \overline{S} (f; σ^{'}), \underline{S} (f; σ) ⩾ \underline{S} (f; σ^{'}) .

这个的证明也是显然的.

我们定义 $\overline{D} (f) = σ \in S (I) in f \overline{S} (f; σ), \underline{D} (f) = σ \in S (I) sup \underline{S} (f; σ) .$ 下面的命题将 Darboux 上下和与上下积分联系起来:

命题 19.3. 假设 $f : I \to R$ 是有界函数, 那么 $\overline{D} (f) = \overline{\int_{a}^{b}} f, \underline{D} (f) = \underline{\int}_{a}^{b} f .$

证明. 根据对称性, 我们证明 $\underline{D} (f) = \underline{\int}_{a}^{b} f$ 即可. 证明分为两步.

•

按照定义, 对任意的 $σ$ , 我们定义函数 $ϕ ∣ ∣_{[a_{i - 1}, a_{i})} = m_{i} (1 ⩽ i ⩽ n)$ , $ϕ (b) = m_{n}$ , 从而 $ϕ \in \underline{E_{f}} (I)$ . 另外, 我们有 $\underline{S} (f; σ) = \int_{a}^{b} ϕ$ . 按照下积分的定义, 我们有 $\int_{a}^{b} ϕ ⩽ \underline{\int}_{a}^{b} f$ , 从而 $\underline{S} (f; σ) ⩽ \underline{\int}_{a}^{b} f$ . 再用 $\underline{D} (f)$ 的定义 (对 $σ$ 取上确界) , 我们得到 $\underline{D} (f) ⩽ \underline{\int}_{a}^{b} f .$

•

其次, 对任意选定的 $ε$ , 按照下极限的定义, 我们可以选取 $ψ \in \underline{E_{f}} (I)$ (其中 $σ_{0} = {b_{0} < b_{1} < \dots < b_{ℓ}}$ 是相应的分划) , 使得 $\underline{\int}_{a}^{b} f ⩽ ε + \int_{a}^{b} ψ .$ 按照定义, 我们知道 $ψ (x) ⩽ f (x)$ . 我们现在任意选取 $I$ 的分划 $σ = {a_{0} < a_{1} < \dots < a_{n}}$ , 我们想要比较 $\int_{a}^{b} ψ$ 和 $\underline{S} (f; σ)$ : $\int_{a}^{b} ψ - \underline{S} (f; σ) = i = 1 \sum n \int_{a_{i - 1}}^{a_{i}} (ψ - m_{i})$

现在有两个分划 $σ_{0}$ 和 $σ$ , 我们需要讨论它们之间的相对关系. 假设 $i$ 是固定的, 那么我们有两种情况:

∘	情形 1: $[a_{i - 1}, a_{i}]$ 中不包含 $σ_{0}$ 的任何一个分割点 $b_{k}$ . 此时, $ψ$ 在 $[a_{i - 1}, a_{i}]$ 的取值是常数. 特别地, 根据 $ψ (x) ⩽ f (x)$ , 我们知道 $ψ (x) ⩽ [a_{i - 1}, a_{i}] in f f (x) = m_{i}$ , 从而 $\int_{a_{i - 1}}^{a_{i}} (ψ (x) - m_{i}) ⩽ 0.$
∘	情形 2: $[a_{i - 1}, a_{i}]$ 中包含某个 $σ_{0}$ 的 (恰好一个, 如果我们假设 $∣ σ ∣$ 足够小) 一个分割点 $b_{k_{0}}$ . 此时, 我们用 $M = x \in I sup f (x)$ 来控制 $ψ (x)$ , 从而有 $∣ ∣ \int_{a_{i - 1}}^{a_{i}} ψ (x) - m_{i} ∣ ∣ ⩽ (a_{i} - a_{i - 1}) (M - m) ⩽ ∣ σ ∣ (M - m) .$ 其中 $m = x \in I in f f (x)$ .

综合上述两种情况, 我们得到 $\int_{a}^{b} ψ - \underline{S} (f; σ) ⩽ 第一种情况 0 + 第二种情况 2 (2 ℓ + 1) 第二种区间的个数 ∣ σ ∣ (M - m) .$ 只要取得 $∣ σ ∣$ 足够小, 我们就得到 $\int_{a}^{b} ψ ⩽ \underline{S} (f; σ) + ε ⩽ \underline{D} (f) + ε,$ 即 $\underline{\int}_{a}^{b} f ⩽ \underline{D} (f) + 2 ε .$ 令 $ε \to 0$ , 我们得到 $\underline{D} (f) ⩾ \underline{\int}_{a}^{b} f .$

命题得到了证明.

$□$

注记. 课后, 有同学讲第二步可以很简单地证明:

对任意的 $φ \in \underline{E_{f}} (I)$ , 选取与 $φ$ 相容的分划 $σ = {a_{0} < a_{1} < \dots < a_{n}}$ , 此时, 由于 $φ ∣ ∣_{(a_{i - 1}, a_{i})} \equiv φ_{i}$ 是常数并且 $φ ⩽ f$ , 所以, $φ_{i} ⩽ m_{i}$ . 据此, 我们知道 $\int_{a}^{b} φ = i = 1 \sum n φ_{i} (a_{i} - a_{i - 1}) ⩽ i = 1 \sum n (a_{i} - a_{i - 1}) m_{i} = \underline{S} (f; σ) .$ 从而, 对任意的 $φ \in \underline{E_{f}} (I)$ $\int_{a}^{b} φ ⩽ σ \in S (I) sup \underline{S} (f; σ) = \underline{D} (f) .$ 再对所有可能的 $φ$ 取上确界即可.

名字空间

视图

19. Riemann 和与 Darboux 上下和