10.6. 残差分析初步

在以上几节内容中, 我们基本上都假定了线性回归模型 (10.1.1) 能够很好地描述自变量 $x$ 与因变量 $Y$ 之间的依赖关系, 且在区间估计与假设检验问题中我们进一步假定了随机误差服从正态分布. 具体而言, 我们做出了如下 4 条假设:

1.	$x_i$ 与 $Y_i$ 之间具有近似的线性关系. 换句话说, 存在实数 ${\beta }_0,{\beta }_1$ 使得 $Y_i={\beta }_0+{\beta }_1{x}_i+{\epsilon }_i$, 其中 ${\epsilon }_i$ 为期望为 $0$ 的随机误差;
2.	每个 ${\epsilon }_i$ 均具有相同的方差 (方差齐性);
3.	${\epsilon }_i$ 之间相互独立;
4.	每个 ${\epsilon }_i$ 均服从正态分布.

但许多情况下, 除了观测到的样本值 $(x_1,y_1),\dots ,(x_n,y_n)$ 以外, 我们可能并没有足够的先验证据证实上述全部 4 条假设, 因此需要根据观测到的样本值来分析上述假设是否合理. 这种对模型假设合理性的分析通常被称为残差分析 (residual analysis), 这是因为大多数相关方法都是以残差这个量为核心的.

本节中我们对最基本也是最常用的残差分析方法进行介绍, 这些方法都是定性或半定量而非完全定量的图示方法, 但在实践中通常都能发挥重要作用. 以下均用 $(x_1,y_1),\dots ,(x_n,y_n)$ 表示一组样本的观测值, 而 ${\hat{\beta }}_0$, ${\hat{\beta }}_1$, $e_i$, ${\hat{y}}_i={\hat{\beta }}_0+{\hat{\beta }}_1{x}_i$ 等则代表相应的统计量在这组样本上的取值.

残差散点图. 残差散点图, 是指将各个 $(x_i,e_i)$ 或 $({\hat{y}}_i,e_i)$ 绘于二维坐标平面上而得到的散点图 ¹. 在前面我们已经分析过, 若样本的产生服从线性回归模型, 且 ${\hat{\beta }}_0$ 与 ${\hat{\beta }}_1$ 是 ${\beta }_0$ 与 ${\beta }_1$ 实际值的良好近似, 则可以近似认为 $e_i\approx {\epsilon }_i$. 这意味着, 在上面提到的前 3 条假设都满足的情况下, 残差散点图中的各个点应当是随机而大致均匀地分布在 $x$ 轴上下两侧、不同横坐标处的残差之间不存在明显的变化规律, 且残差上下波动的幅度在横坐标变化时近似保持一致.

图 1. 几个典型的残差散点图示例.

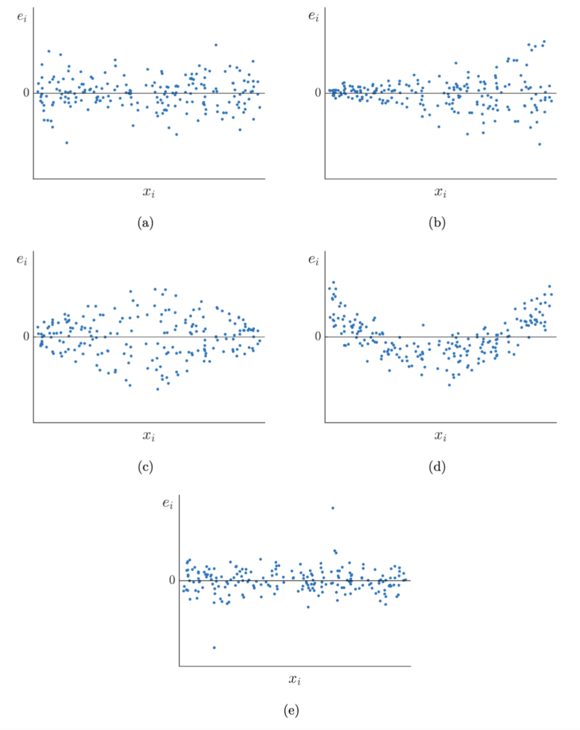
图 1 给出了几种典型的残差散点图的示例, 直观上看,

1.	图 1(b) 与 1(c) 表明随机误差 ${\epsilon }_i$ 的方差并不相同, 也就是说方差齐性的假设被破坏.
2.	图 1(d) 表明, 因变量 $x$ 与自变量 $Y$ 之间存在未被模型刻画的非线性关系.
3.	图 1(e) 则表明, 数据当中可能存在异常值, 此时需要采用其它方法对异常值等进行辨识.

而图 1(a) 所示的残差散点图则直观上看是比较正常、与线性回归模型假设无明显冲突的.

在画残差散点图之前, 我们还可以先将残差进行归一化. 由第 10.2 节第 3 小节的计算可知, 当线性回归模型假设得到满足时, 有$$\mathrm{Var}(e_i)={\sigma }^2\left(1-\frac{1}{n}-\frac{(x_i-\overline{x}{)}^2}{S_{xx}}\right),$$故我们可以令$$t_i=\frac{e_i}{\sqrt{\widehat{{\sigma }^2}\left(1-\frac{1}{n}-\frac{(x_i-\overline{x}{)}^2}{S_{xx}}\right)}},$$而后画 $(x_i,t_i),i=1,\dots ,n$ 的散点图. $t_i$ 则被称为 Studentized residual. 通常, 若样本点 $(x_i,y_i),i=1,\dots ,n$ 当中存在个别点的 $x_i$ 与 $\overline{x}$ 相差很大, 使得 $(x_i-\overline{x}{)}^2/S_{xx}$ 与 $1$ 相比不可忽略, 则这些点的残差的方差相比于其它点在理论上就是明显偏小的, 此时用 Studentized residual 的散点图进行残差分析是更加合理的.

关于残差的其它归一化方法可参考 [30] 第 4.2.2 节.

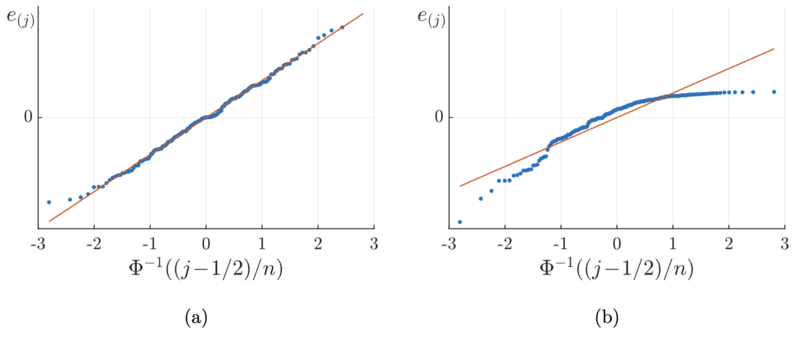
(${}^{\star }$) 正态概率图. 正态概率图是用于判断随机误差 $\epsilon$ 是否服从正态分布 $\mathcal{N}(0,{\sigma }^2)$ 的定性方法. 具体而言, 设我们已经对前 3 条假设的合理性进行了验证. 将残差 $e_1,\dots ,e_n$ 由小到大进行排序, 得到$$e_{(1)}<e_{(2)}<\cdots <e_{(n)}.$$由于 $e_i\approx {\epsilon }_i$, 当样本容量 $n$ 足够大且各个 ${\epsilon }_i$ 服从正态分布时, 应当有$$\begin{array}{rl}\Phi \left(\frac{t}{\sigma }\right)\approx & \frac{1}{n}\sum _{i=1}^n\frac{1_{\{{\epsilon }_i\le t\}}+1_{\{{\epsilon }_i<t\}}}{2}\\ \approx & \frac{1}{n}\sum _{i=1}^n\frac{1_{\{e_i\le t\}}+1_{\{e_i<t\}}}{2}\\ =& \frac{\max \{i\mid e_{(i)}\le t\}+\max \{i\mid e_{(i)}<t\}}{2n},\end{array}$$其中第一个约等号来自于用经验分布函数近似分布函数, 且加入了类似于连续性修正的步骤. 在上式中将 $t=e_{(j)}$ 代入, 即可得到$$\begin{array}{rl}\Phi \left(\frac{e_{(j)}}{\sigma }\right)\approx & \frac{\max \{i\mid e_{(i)}\le e_{(j)}\}+\max \{i\mid e_{(i)}<e_{(j)}\}}{2n}\\ =& \frac{j+(j-1)}{2n}=\frac{j-1/2}{n},\end{array}$$从而$$e_{(j)}\approx \sigma \cdot {\Phi }^{-1}\left(\frac{j-1/2}{n}\right).$$上式意味着, 在随机误差的正态性假设得到满足的情况下, 如果我们将各个点$$\left({\Phi }^{-1}\left(\frac{j-1/2}{n}\right),e_{(j)}\right),j=1,\dots ,n$$画在二维坐标平面上得到一散点图, 则这些点应落于过原点的某条直线附近, 该散点图被称为正态概率图 (normal probability plot) ²; 利用 ${\sigma }^2$ 的点估计值 $\widehat{{\sigma }^2}={SS}_{\mathrm{Res}}/(n-2)$, 我们还可以在正态概率图上作出直线 $y=\sqrt{\widehat{{\sigma }^2}}x$ 以和图上的散点进行比对. 图 2 给出了两种典型的正态概率图, 其中图 2(a) 意味着观测到的样本与随机误差的正态性假设无明显冲突, 而图 2(b) 则意味着随机误差的正态性假设很有可能是被打破的.

图 2. 几个典型的正态概率图示例.

脚注

1.	^ 对于一元线性回归, 横坐标用 $x_i$ 或 ${\hat{y}}_i$ 均可, 它们给出的散点图具有相似关系.
2.	^ 有些地方将正态概率图的横坐标取为 $e_{(j)}$ 而纵坐标取为 ${\Phi }^{-1}((j-1/2)/n)$. 此外, 在绘制正态概率图时也可用归一化残差 (如 Studentized residual $t_i$) 来代替原始残差 $e_i$.