6.2. 重要抽样分布
统计量的概率分布被称为抽样分布. 本节中我们将研究一些与正态总体相关的抽样分布, 这些抽样分布将对本讲义介绍的统计推断方法的理论分析起到重要作用.
分布 (卡方分布)
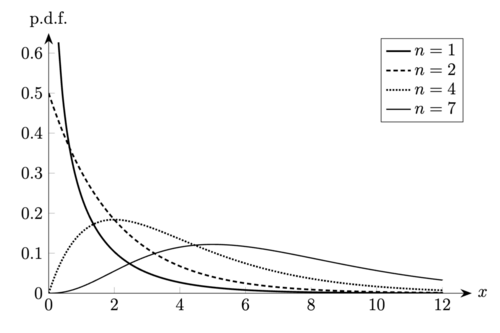
我们称随机变量 服从自由度为 的 分布 ( distribution 或 chi-squared distribution), 若 为连续型随机变量, 且其概率密度函数为其中 为一正整数. 我们用 或 来指代自由度为 的 分布, 并用 或 表示 服从自由度为 的 分布. 图 1 给出了 分布概率密度函数的典型图像.
我们马上将看到, 分布与来自正态总体的样本方差的分布直接相关. 接下来先给出 分布自身的一些性质.
命题 6.2.1. 设 服从自由度为 的 分布, 则其矩母函数为其期望为 , 方差为 .
证明. 我们有不难看出 时 不存在. 而当 时, 有其中做了换元 并利用了 函数的定义.
推论 6.2.2.
1. | 设 相互独立且各自服从自由度为 的 分布, 则 服从自由度为 的 分布. |
2. | 设 相互独立且均服从一元标准正态分布 , 则 服从自由度为 的 分布. |
证明.
1. | 我们考虑 的矩母函数, 由定理 4.3.6 可得故 服从自由度为 的 分布. |
2. |
在经过上述准备后, 我们介绍定理 6.2.3, 它给出了 分布最重要的应用场合: 刻画来自正态总体的样本方差的分布; 该定理也与下一节介绍的 分布的重要性质密切相关. 定理的证明由于牵扯到一些连续型随机向量仿射变换 (推论 4.1.10) 以及实对阵矩阵正交对角化的知识, 故作为选读内容放在第 6.3 节第 1 小节给出, 但我们鼓励学有余力的读者掌握这个证明.
定理 6.2.3. 设 为正态总体 的一组样本. 令 为其样本均值, 为其样本方差. 则
1. | 与 相互独立. |
2. | 随机变量服从自由度为 的 分布. |
分布
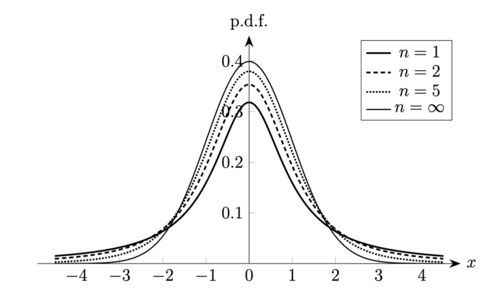
我们称随机变量 服从自由度为 的 分布 ( distribution 或 Student’s distribution 1), 若 为连续型随机变量, 且其概率密度函数为其中 为一正整数. 我们用 或 来指代自由度为 的 分布, 并用 或 表示 服从自由度为 的 分布. 图 2 给出了 分布概率密度函数的典型图像, 其中 的情形实际上考虑的是 时分布 的概率密度函数的极限; 可以证明固定 时, 有 2这说明分布 的概率密度函数在 时将逐点收敛于标准正态分布的概率密度函数.
以下定理给出了 分布的由来, 其证明作为选读内容将在第 6.3 节第 2 小节给出.
定理 6.2.4. 设 且 相互独立. 不妨设 的值域不包含 . 则随机变量服从自由度为 的 分布.
将定理 6.2.4 与定理 6.2.3 结合, 可得到如下重要推论.
推论 6.2.5. 设 为正态总体 的一组样本. 令其中 为样本均值, 为样本方差. 则统计量 服从自由度为 的 分布.
需要注意, 推论 6.2.5 当中我们必须要求 相互独立且均服从正态分布 ; 若样本 不是从正态总体中抽样得来的, 即使 非常大, 我们也不能因为中心极限定理而认为推论 6.2.5 成立.
分布
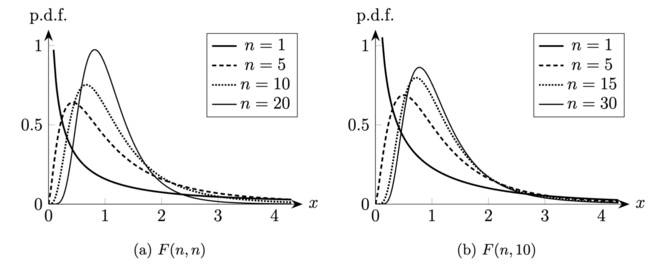
我们称随机变量 服从自由度为 的 分布 3, 若其概率密度函数为其中 均为正整数. 我们用 来指代自由度为 的 分布, 并用 表示 服从自由度为 的 分布. 图 3 给出了 分布概率密度函数的典型图像.
以下定理给出了 分布的由来, 其证明作为选读内容将在第 6.3 节第 3 小节给出.
推论 6.2.7. 设 为总体 的一组样本, 为总体 的一组样本, 且 相互独立. 令则
抽样分布的上分位数
上面三个小节给出了 分布、 分布与 分布的概率密度函数. 但对于许多数理统计问题, 更常用的其实是这些抽样分布的上分位数.
定义 6.2.8. 设 为一连续型分布的分布函数, 其概率密度函数为 . 进一步假设 在某个开区间 上严格大于 而在该开区间外等于 . 则对任意 , 我们将满足的实数 称作分布 的上 分位数 ( quantile). 换句话说, 若随机变量 的分布函数为 , 则 大于等于上 分位数的概率就等于 .
注 6.2.9. 对于更加一般的分布也可定义其上分位数, 但在本课程中, 我们只需考虑定义 6.2.8 所讨论的情形就足够了.
不难验证, 若某个分布满足定义 6.2.8 中所列出的条件, 则它的上 分位数是关于 的连续且严格单调递减的函数.
下面我们讨论几个重要分布的上分位数.
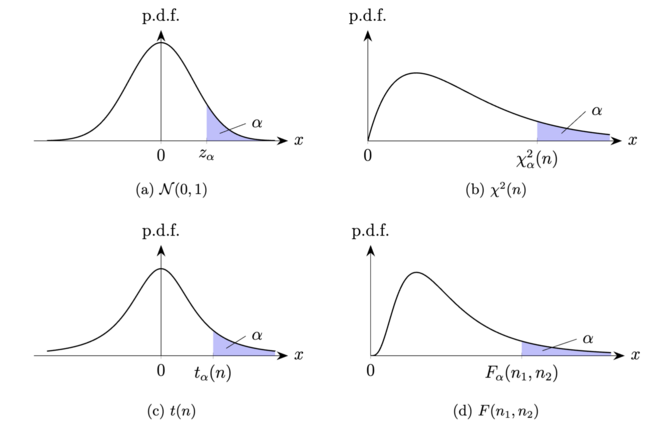
标准正态分布. 对于标准正态分布 , 我们将其上 分位数记作 , 也就是说 由如下等式给出: 若用 表示 的反函数, 则有图 4(a) 给出了 的图示. 不难看出 时 , 以及 时 . 此外, 由 可得
分布. 对于自由度为 的 分布, 我们将其上 分位数记作 . 图 4(b) 给出了 的图示. 不难看出 时 , 以及 时 . 此外, 我们通常会将 记作 .
分布. 对于自由度为 的 分布, 我们将其上 分位数记作 . 图 4(c) 给出了 的图示. 不难看出 时 , 以及 时 . 此外, 由分布 的概率密度函数的对称性, 可得经验上, 当 时, 对于常用的 的值, 我们会采用近似 , 这是因为 足够大时, 的概率密度函数 (以及分布函数) 可以被标准正态分布的概率密度函数 (以及分布函数) 很好地近似.
分布. 对于自由度为 的 分布 , 我们将其上 分位数记作 . 图 4(d) 给出了 的图示. 不难看出 时 , 以及 时 . 此外, 分布的上分位数满足如下性质: (6.2.1)这是因为 时有从而而由 分布的性质可知 , 故上式即意味着 .
需要指出的是, 以上讨论的几个分布的上 分位数通常都不能表示为 的初等函数. 我们一般是通过查表或是数值计算的方法来获取这些上 分位数的值. 表 1 列出了一些常用编程语言中用于计算上分位数的表达式.
| Python 3 | R | MATLAB | |
| norm.isf() | qnorm(1-) | norminv(1-) | |
| chi2.isf(, ) | qchisq(1-, df=) | chi2inv(1-, ) | |
| t.isf(, ) | qt(1-, df=) | tinv(1-, ) | |
| f.isf(, , ) | qf(1-, df1=, df2=) | finv(1-, , ) |
注: Python 3 中需安装库 SciPy 并加入导入语句 from scipy.stats import *
脚注
1. | ^ 这里的 Student 来自于统计学家 William Sealy Gosset 使用的一个假名, 他在 1908 年发表于 Biometrika 的论文 “The probable error of a mean” 中用 Student 来署名. 之后著名统计学家 Ronald Fisher 在其工作中将这个分布称作 “Student’s distribution”, 并用 作为相应统计量的符号, “Student’s distribution” 这个名称也就逐渐被广泛接受. |
2. | ^ 该极限可由斯特林公式出发证明. |
3. | ^ 分布又被称作 Snedecor’s distribution、the Fisher–Snedecor distribution 等. 统计学家 Ronald Fisher 于 1922 年首次给出了 分布的形式, 而统计学家 George W. Snedecor 将其用 分布命名, 以纪念 Ronald Fisher. |