4.6. 习题选编

习题 4.6.1 (柯西分布). 设随机变量 $X$ 服从 $\left]-\pi /2,\pi /2\right[$ 上的均匀分布, 令 $Y=\tan X$.

1.	证明 $Y$ 为连续型随机变量, 并求其概率密度函数. 注: 我们称 $Y$ 服从的分布为标准柯西分布 (standard Cauchy distribution).
2.	判断 $Y$ 的期望是否存在, 并给出依据.

习题 4.6.2. 设 $X$ 为一随机变量, 其分布函数为 $F(x)=\mathbb{P}(X\le x),x\in \mathbb{R}$. 若 $F$ 在 $\mathbb{R}$ 上连续且严格单调递增, 证明随机变量 $F(X)$ 服从 $\left]0,1\right[$ 上的均匀分布.

习题 4.6.3. 设 $X,Y$ 相互独立, 且 $X$ 服从参数为 $(s,\lambda )$ 的 Gamma 分布, $Y$ 服从参数为 $(t,\lambda )$ 的 Gamma 分布. 证明 $X+Y$ 服从参数为 $(s+t,\lambda )$ 的 Gamma 分布.

注: Gamma 分布的定义由例 4.1.7 当中的式 (4.1.1) 给出.

习题 4.6.4. 设随机变量 $T_1,T_2,\dots$ 相互独立且服从参数为 $\lambda$ 的指数分布. 令$$N=\max \left\{k\in {\mathbb{N}}_{+}\mid T_1+\cdots +T_k\le t\right\}.$$证明 $N$ 服从参数为 $\lambda t$ 的泊松分布.

提示: 利用 $\{N\ge k\}=\{T_1+\cdots +T_k\le t\}$ 计算 $\mathbb{P}(N\ge k)$, 而后用分部积分处理得到的定积分式.

习题 4.6.5. 设一个银行有 $m$ 个窗口, 每个窗口为单个顾客办理业务的时间服从参数为 $\lambda$ 的指数分布, 来到银行的顾客需要先叫号并排成一队, 当某个窗口空出来时, 排在队首的顾客将到该窗口办理业务. 某一天你来到该银行办理业务, 发现前面共有 $n$ 个人正在排队或正在窗口 (其中 $n\ge m$), 令 $T$ 表示你的排队时间, 试求 $T$ 的分布.

提示: 令 $N_i(t)$ 表示 $t$ 时刻第 $i$ 个窗口已接待 (包括正在接待) 的人数, 利用习题 4.6.4 的结论求出 $N_i(t)$ 的分布, 并说明 $N_1(t),\dots ,N_m(t)$ 相互独立 (不要求严格证明), 再利用 $\mathbb{P}(T>t)=\mathbb{P}(N_1(t)+\cdots +N_m(t)\le n)$.

习题 4.6.6. 设 $X,Y$ 为相互独立的连续型随机变量, 概率密度函数分别为 $f_X,f_Y$.

1.	证明随机变量 $XY$ 为连续型随机变量, 且概率密度函数为$$f_{XY}(z)={\int }_{-\infty }^{+\infty }\frac{1}{|x|}{f}_X(x)f_Y\left(\frac{z}{x}\right)\mathrm{d}x,z\in \mathbb{R}$$
2.	设 $0\notin \mathrm{Im}X$. 证明 $Y/X$ 为连续型随机变量, 且概率密度函数为$$f_{Y/X}(z)={\int }_{-\infty }^{+\infty }|x|f_X(x)f_Y(zx)\mathrm{d}x,z\in \mathbb{R}.$$

习题 4.6.7. 令 $X_1,\dots ,X_n$ 为独立同分布的随机变量且服从 $\left]0,1\right[$ 上的均匀分布, 其中 $n\ge 2$. 记$$X_{(1)}=\min \{X_1,\dots ,X_n\},X_{(n)}=\max \{X_1,\dots ,X_n\}.$$

1.	证明 $(X_{(1)},X_{(n)})$ 为二维连续型随机向量, 并求出它的联合概率密度函数. 提示: 先求出 $\mathbb{P}(X_{(1)}>u,X_{(n)}\le v),(u,v)\in {\mathbb{R}}^2$.
2.	求 $X_{(n)}-X_{(1)}$ 服从的概率分布.

习题 4.6.8. 设 $X,Y$ 为随机变量且 $\mathrm{Var}(X)>0$, $\mathrm{Var}(Y)>0$, $X$ 与 $Y$ 的相关系数记为 ${\rho }_{XY}$. 证明

1.	${\rho }_{XY}=1$ 当且仅当存在 $c>0$ 使得 $Y-\mathbb{E}[Y]=c(X-\mathbb{E}[X])$ 几乎必然成立.
2.	${\rho }_{XY}=-1$ 当且仅当存在 $c<0$ 使得 $Y-\mathbb{E}[Y]=c(X-\mathbb{E}[X])$ 几乎必然成立.

习题 4.6.9. 设 $X_1,\dots ,X_n$ 为独立同分布的随机变量, 且期望 $\mathbb{E}[X_1]$ 与方差 $\mathrm{Var}(X_1)$ 均存在. 令 $\overline{X}=\frac{1}{n}{\sum }_{i=1}^n{X}_i$. 证明对任意 $j=1,\dots ,n$, $X_j-\overline{X}$ 与 $\overline{X}$ 不相关.

习题 4.6.10 (贝叶斯公式).

1.	设 $(X,Y)$ 为离散型随机向量. 证明 $p_X(x)>0$ 时有$$p_{Y|X}\left(y|x\right)=\frac{p_{X|Y}\left(x|y\right)p_Y(y)}{{\sum }_{y^{\prime }}{p}_{X|Y}\left(x|y^{\prime }\right)p_Y(y^{\prime })}.$$
2.	设 $(X,Y)$ 为连续型随机向量. 证明 $f_X(x)>0$ 时有$$f_{Y|X}\left(y|x\right)=\frac{f_{X|Y}\left(x|y\right)f_Y(y)}{{\int }_{-\infty }^{+\infty }{f}_{X|Y}\left(x|y^{\prime }\right)f_Y(y^{\prime })\mathrm{d}{y}^{\prime }}.$$

习题 4.6.11. 设 $(X,Y)$ 为连续型随机向量, 且对任意 $(x,y)\in {\mathbb{R}}^2$ 均有 $f_{Y|X}\left(y|x\right)>0$ 及 $f_{X|Y}\left(x|y\right)>0$.

1.	证明$$f_X(x)={\left({\int }_{-\infty }^{+\infty }\frac{f_{Y|X}\left(y|x\right)}{f_{X|Y}\left(x|y\right)}\mathrm{d}y\right)}^{-1},\forall x\in \mathbb{R},$$
2.	对任意 $(x,y)\in {\mathbb{R}}^2$, 试用 $f_{X|Y}\left(x|y\right)$ 与 $f_{Y|X}\left(y|x\right)$ 表示 $f_{X,Y}(x,y)$.

习题 4.6.12. 设 $X,Y$ 为随机变量, 且 $\mathbb{E}[X]$ 存在. 证明 $\mathbb{E}\left[X|Y\right]$ 与 $X-\mathbb{E}\left[X|Y\right]$ 不相关.

习题 4.6.13. 给定随机变量 $X$ 与 $Y$, 设 $X$ 的方差存在. 证明$$\mathrm{Var}(X)=\mathbb{E}\left[\mathrm{Var}\left(X|Y\right)\right]+\mathrm{Var}\left(\mathbb{E}\left[X|Y\right]\right).$$

习题 4.6.14. 设 $X,Y$ 为相互独立的随机变量. $X$ 为离散型随机变量, 其分布列为 $p_X$; $Y$ 为连续型随机变量, 其概率密度函数为 $f_Y$. 证明 $Z=X+Y$ 为连续型随机变量, 并求出 $Z$ 的概率密度函数.

习题 4.6.15. 假设有一名工程师需要每天到机房进行设备维护. 取上午 9 点为 0 时刻, 该工程师到达机房的时刻 $Y$ 是随机的, 且服从 $\left]0,3\right[$ 上的均匀分布. 他维护设备需要花费的时间 $T$ 也是随机的, 且在 $Y=y$ 的条件下服从参数为 $\lambda (y)=1/(4-y)$ 的指数分布. 工程师完成设备维护后就离开机房.

1.	试求维护设备花费时间 $T$ 的期望与方差.
2.	试求工程师离开机房的时刻的期望.
3.	现假设工程师的一名同事每天需要去机房做实验, 同事每天到达机房的时刻服从 $\left]0,8\right[$ 上的均匀分布. 若同事到达机房时工程师仍在进行设备维护, 则工程师需要暂停他的维护工作, 等同事完成实验, 再继续维护工作. 设同事的实验所耗费的时间服从 $\left]0,1\right[$ 上的均匀分布, 且不影响工程师维护设备总共花费的时间. 试求该情形下工程师离开机房的时刻的期望.

注: 本题改编自 [5] 第四章习题 24.

习题 4.6.16. 假设有一根长度为 $1$ 的直杆, 我们用如下三种方式将这跟直杆切成三段:

1.	在直杆上均匀且独立地随机取两点, 将杆在这两点处切为三段.
2.	在直杆上均匀地随机选取一个点切成两段, 再在两段中较长的那一段上均匀地随机取一个点切开.
3.	在直杆上均匀地随机选取一个点切成两段, 再在两段中等概率地随机挑一段并将其等分.

试求上述三种情形下, 切出来的三段能够构成一个三角形的概率.

习题 4.6.17. 设连续型随机变量 $X_1,X_2$ 相互独立, 且均服从标准正态分布 $\mathcal{N}(0,1)$, 即$$f_{X_1}(x)=f_{X_2}(x)=\frac{1}{\sqrt{2\pi }}\exp \left(-\frac{x^2}{2}\right).$$

1.	任取 $z\in \mathbb{R}$, 试求随机变量$$Y_z=\frac{1}{\sqrt{1+z^2}}{X}_1+\frac{z}{\sqrt{1+z^2}}{X}_2$$的概率分布.
2.	设 $Z$ 为一离散型随机变量, 且 $X_1,X_2,Z$ 相互独立. 试求随机变量$$Y=\frac{1}{\sqrt{1+Z^2}}{X}_1+\frac{Z}{\sqrt{1+Z^2}}{X}_2$$的概率分布.
3.	设 $Z$ 为连续型随机变量, 且 $X_1,X_2,Z$ 相互独立, 试求随机变量$$Y=\frac{1}{\sqrt{1+Z^2}}{X}_1+\frac{Z}{\sqrt{1+Z^2}}{X}_2$$的概率分布. 提示: 考虑 $F_Y(y)=\mathbb{P}(Y\le y)$ 并利用全期望公式 $\mathbb{P}(Y\le y)=\mathbb{E}\left[\mathbb{E}\left[1_{\{Y\le y\}}|Z\right]\right]$.

习题 4.6.18 (Borel–Kolmogorov 悖论). 记 $S^2:=\left\{(x,y,z)\in {\mathbb{R}}^3\mid x^2+y^2+z^2=1\right\}$ 为 ${\mathbb{R}}^3$ 中球心位于原点的单位球面. 设 3 维随机向量 $(X,Y,Z)$ 满足 $(X,Y,Z)\in S^2$, 且对单位球面上任意面积可求的区域 $B\subset S^2$, 有$$\mathbb{P}((X,Y,Z)\in B)=\frac{1}{4\pi }{\iint }_B\mathrm{d}A,$$其中 $\mathrm{d}A$ 表示单位球面 $S^2$ 上的面元; 换句话说, $(X,Y,Z)$ 服从单位球面上的均匀分布.

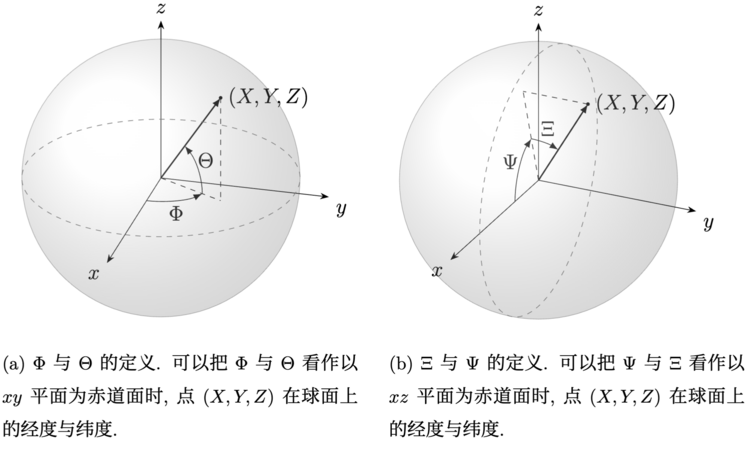
1.	令随机变量 $\Phi$ 与 $\Theta$ 表示图 1(a) 所定义的角度, 其中 $-\pi <\Phi \le \pi$, $-\pi /2\le \Theta \le \pi /2$, 且规定 $X=Y=0$ 时 $\Phi =0$. 证明 $(\Phi ,\Theta )$ 为连续型随机向量, 且它的联合概率密度函数为$$f_{\Phi ,\Theta }(\phi ,\theta )=\{\begin{array}{ll}\frac{1}{4\pi }\cos \theta ,& \text{若}-\pi <\phi \le \pi ,|\theta |\le \frac{\pi }{2},\\ 0,& \text{其他情况}.\end{array}$$
2.	现令随机变量 $\Xi$ 与 $\Psi$ 表示图 1(b) 所定义的角度, 其中 $-\pi /2\le \Xi \le \pi /2$, $-\pi <\Psi \le \pi$, 且规定 $X=Z=0$ 时 $\Psi =0$. 证明 $(\Xi ,\Psi )$ 的联合概率密度函数为$$f_{\Xi ,\Psi }(\xi ,\psi )=\{\begin{array}{ll}\frac{1}{4\pi }\cos \xi ,& \text{若}|\xi |\le \frac{\pi }{2},-\pi <\psi \le \pi ,\\ 0,& \text{其他情况}.\end{array}$$
3.	由前两小题给出的联合概率密度, 计算条件概率密度 $f_{\Phi |\Theta }\left(\phi |\theta \right)$ 以及 $f_{\Xi |\Psi }\left(\xi |\psi \right)$.
4.	证明: 对任意区间 $I\subseteq \left[-\frac{\pi }{2},\frac{\pi }{2}\right]$, 均有$$\{\Phi \in I,\Theta =0\}=\{\Xi \in I,\Psi =0\},$$但等式$${\int }_I{f}_{\Phi |\Theta }\left(\phi |0\right)\mathrm{d}\phi ={\int }_I{f}_{\Xi |\Psi }\left(\xi |0\right)\mathrm{d}\xi$$一般不成立.

图 1. 习题 4.6.18 图示.

习题 4.6.19 (Rejection sampling). 设非负函数 $f,g:\mathbb{R}\to \left[0,+\infty \right[$ 与常数 $c$ 满足

•	${\int }_{-\infty }^{+\infty }f(x)\mathrm{d}x={\int }_{-\infty }^{+\infty }g(x)\mathrm{d}x=1$;
•	$g(x)>0,\forall x\in \mathbb{R}$;
•	$\frac{f(x)}{g(x)}\le c,\forall x\in \mathbb{R}$.

现令 $U_1,Y_1,U_2,Y_2,\dots$ 为相互独立的连续型随机变量, 且每个 $U_n$ 服从 $[0,1]$ 上的均匀分布, 每个 $Y_n$ 的概率密度函数均为 $g$, 再令$$X=Y_N,\text{其中}N=\min \left\{n|U_n\le \frac{f(Y_n)}{c\cdot g(Y_n)}\right\}.$$

1.	证明 $X$ 的分布函数为$$F_X(x)=\mathbb{P}\left(Y_1\le x|U_1\le \frac{f(Y_1)}{c\cdot g(Y_1)}\right).$$
2.	证明$$\mathbb{P}\left(U_1\le \frac{f(Y_1)}{c\cdot g(Y_1)}\right)=\frac{1}{c}.$$
3.	证明$$\mathbb{P}\left(Y_1\le x,U_1\le \frac{f(Y_1)}{c\cdot g(Y_1)}\right)=\frac{1}{c}{\int }_{-\infty }^{x}f(t)\mathrm{d}t,$$从而 $X$ 的概率密度函数为 $f$.
4.	设有两个随机数生成器, 一个生成的随机数服从 $[0,1]$ 上的均匀分布, 另一个生成的随机数具有概率密度函数 $g$. 说明如何用这两个随机数生成器生成一个概率密度函数为 $f$ 的随机数.

习题 4.6.20. 设 $f:\{1,2,\dots ,n\}\to \mathbb{R}$ 为一函数, 且 $x\ne y$ 时 $f(x)\ne f(y)$. 假设我们并不知道 $f$ 在每个点的取值, 但有一个黑箱, 当我们把 $x\in \{1,\dots ,n\}$ 输入这个黑箱后, 这个黑箱会输出集合 $S_x=\left\{y\in \{1,\dots ,n\}\mid f(y)>f(x)\right\}$. 为了利用这个黑箱找出使得 $f(x)$ 取得最大值的 $x$, 我们考虑如下算法:

1.	从 $\{1,\dots ,n\}$ 中等概率地随机选一个点作为 $X_0$, 并利用黑箱得到集合 $S_{X_0}$;
2.	若 $S_{X_0}=\varnothing$ 则输出 $X_0$, 算法结束; 否则执行接下来的步骤;
3.	令 $k\leftarrow 0$;
4.	repeat
5.	$k\leftarrow k+1$;
6.	从 $S_{X_{k-1}}$ 中等概率地随机选择一个点作为 $X_k$;
7.	利用黑箱得到集合 $S_{X_k}$;
8.	until $S_{X_k}=\varnothing$
9.	输出 $X_k$.

不难看出上述算法最终的输出结果的确能使得 $f$ 取到最大值. 现令随机变量 $R$ 表示整个算法从开始到结束的过程中调用黑箱的总次数, 试求 $\mathbb{E}[R]$, 并给出 $n$ 非常大时 $\mathbb{E}[R]$ 的一个近似表达式.

注: 本题改编自 [6] 第 3.11 节习题 33.

习题 4.6.21. (${}^{\star }$) 设 $a,b$ 为给定正实数, 随机变量 $X,Y$ 相互独立, 且 $X$ 服从参数为 $(a,1)$ 的 Gamma 分布, $Y$ 服从参数为 $(b,1)$ 的 Gamma 分布. 令 $U=X+Y,V=X/(X+Y)$.

1.	证明 $U$ 与 $V$ 相互独立, 并求出它们各自的分布.
2.	证明$$\mathbb{E}\left[\frac{X}{X+Y}\right]=\frac{\mathbb{E}[X]}{\mathbb{E}[X]+\mathbb{E}[Y]}.$$

习题 4.6.22. (${}^{\star }$) 设 $X,Y$ 相互独立且均服从正态分布 $\mathcal{N}(0,1)$, 令$$U=X^2+Y^2,V=atan2(Y,X)$$(其中 $atan2(y,x)\in [0,2\pi [$ 表示坐标平面上从原点指向 $(x,y)$ 的射线与 $x$ 轴正方向之间的夹角, $x=y=0$ 时取 $atan2(y,x)=0$). 证明 $U,V$ 相互独立, 并求出 $U,V$ 各自的概率分布.

习题 4.6.23. (${}^{\star }$) 设 $\mathbf{P}\in {\mathbb{R}}^{n\times n}$ 为一实对称正定矩阵, $\mathbf{q}\in {\mathbb{R}}^n$ 为一向量, 令$$f(\mathbf{x})=\exp \left(-\frac{1}{2}{\mathbf{x}}^{\mathsf{T}}\mathbf{P}\mathbf{x}-{\mathbf{q}}^{\mathsf{T}}\mathbf{x}\right),\mathbf{x}\in {\mathbb{R}}^n.$$证明$${\int }_{{\mathbb{R}}^n}f(\mathbf{x})\mathrm{d}\mathbf{x}=\sqrt{\frac{(2\pi {)}^n}{\det \mathbf{P}}}\exp \left(\frac{1}{2}{\mathbf{q}}^{\mathsf{T}}{\mathbf{P}}^{-1}\mathbf{q}\right).$$

提示: 首先对 $-\frac{1}{2}{\mathbf{x}}^{\mathsf{T}}\mathbf{P}\mathbf{x}-{\mathbf{q}}^{\mathsf{T}}\mathbf{x}$ 配方, 将其变形为 $-\frac{1}{2}(\mathbf{x}-{\mathbf{x}}_0{)}^{\mathsf{T}}\mathbf{P}(\mathbf{x}-{\mathbf{x}}_0)+c$ 的形式, 其中 ${\mathbf{x}}_0\in {\mathbb{R}}^n$ 而 $c\in \mathbb{R}$. 再利用 $\mathbf{P}$ 的特征值分解构造矩阵 $\mathbf{B}\in {\mathbb{R}}^{n\times n}$ 使得 ${\mathbf{B}}^{\mathsf{T}}\mathbf{B}=\mathbf{P}$, 最后做换元 $\mathbf{y}=\mathbf{B}(\mathbf{x}-{\mathbf{x}}_0)$ 并利用重积分换元定理 (可参考定理 4.1.8).

习题 4.6.24. (${}^{\star }$) 设 $(X_1,X_2)\sim \mathcal{N}(\mathbf{\mu },\mathbf{\Sigma })$, 其中$$\mathbf{\mu }=\left[\begin{array}{c}{\mu }_1\\ {\mu }_2\end{array}\right],\mathbf{\Sigma }=\left[\begin{array}{cc}{\sigma }_{11}& {\sigma }_{12}\\ {\sigma }_{21}& {\sigma }_{22}\end{array}\right].$$证明给定 $X_2=x_2$ 时 $X_1$ 的条件概率密度函数为$$f_{X_1|X_2}\left(x_1|x_2\right)=c\cdot \exp \left\{-\frac{{\left[x_1-{\mu }_1-{\sigma }_{12}{\sigma }_{22}^{-1}(x_2-{\mu }_2)\right]}^2}{2({\sigma }_{11}-{\sigma }_{12}{\sigma }_{22}^{-1}{\sigma }_{21})}\right\},$$其中 $c$ 为某个 (依赖于 $x_2$ 的) 实数. 换句话说, 给定 $X_2=x_2$ 时 $X_1$ 服从正态分布 $\mathcal{N}({\mu }_1+{\sigma }_{12}{\sigma }_{22}^{-1}(x_2-{\mu }_2),{\sigma }_{11}-{\sigma }_{12}{\sigma }_{22}^{-1}{\sigma }_{21})$.

习题 4.6.25. (${}^{\star }$) 设 $\mathbf{X}=(X_1,X_2)$ 为一随机向量.

1.	证明: 若 $\mathbf{X}$ 服从二维正态分布, 且 $X_1,X_2$ 不相关, 则 $X_1,X_2$ 相互独立.
2.	证明: 设 $X_1,X_2$ 均服从一维正态分布, 且 $X_1,X_2$ 相互独立, 则 $(X_1,X_2)$ 服从二维正态分布.
3.	若 $X_1,X_2$ 均服从一维正态分布, 且 $X_1,X_2$ 不相关, 则 $X_1,X_2$ 是否一定服从二维正态分布? 是否一定相互独立? 请给出证明或构造反例.