5.5. 一些例子

QR 分解

命题 5.5.1 (可逆方阵的 QR 分解). 设 $A$ 是 $n$ 阶可逆方阵, 则存在唯一的分解$$A=QR$$其中 $Q$ 是 $n$ 阶正交方阵, $R$ 是对角元都是正数的上三角矩阵.

证明: 记 $A$ 的列向量为 $A=\left[\begin{array}{ccc}{\vec{\alpha }}_1& \cdots & {\vec{\alpha }}_n\end{array}\right]$. 由 Gram-Schmidt 正交化和归一化的过程, 我们得到一个对角元都是正数的上三角矩阵 $R$ 使得$$\left[\begin{array}{ccc}{\vec{\alpha }}_1& \cdots & {\vec{\alpha }}_n\end{array}\right]=\left[\begin{array}{ccc}{\vec{\beta }}_1& \cdots & {\vec{\beta }}_n\end{array}\right]R$$这里 $\{{\vec{\beta }}_1,\cdots ,{\vec{\beta }}_n\}$ 是标准正交基. 记 $Q=\left[\begin{array}{ccc}{\vec{\beta }}_1& \cdots & {\vec{\beta }}_n\end{array}\right]$, 则 $Q$ 是正交方阵且 $A=QR$.

下证唯一性. 假设有 $Q_1{R}_1=Q_2{R}_2$, 这里 $Q_1,Q_2$ 是正交阵, $R_1,R_2$ 是对角元都是正数的上三角矩阵. 则 $R_1{R}_2^{-1}=Q_1^{-1}{Q}_2$ 是正交阵并且是对角元都是正数的上三角矩阵$$R_1{R}_2^{-1}=\left[\begin{array}{cccc}{a}_{11}& \ast & \cdots & \ast \\ 0& a_{22}& \cdots & \ast \\ \cdots & \cdots & \cdots & \cdots \\ 0& \cdots & 0& a_{nn}\end{array}\right]a_{ii}>0$$

由列向量的标准正交性易知 $R_1{R}_2^{-1}$ 只能是对角阵, 且 $a_{ii}=1$. 即 $R_1{R}_2^{-1}=I_n$. 由此得 $R_1=R_2,Q_1=Q_2$.

$\square$

QR 分解有很多应用. 比如考虑线性方程组$$A\vec{x}=\vec{b}$$这里 $A$ 是可逆矩阵. 我们知道它有唯一解 $\vec{x}=A^{-1}\vec{b}$. 在实际应用中计算矩阵的逆 $A^{-1}$ 通常很复杂. 如果我们有矩阵的 QR 分解 $A=QR$, 则上述方程等价于$$R\vec{x}=Q^T\vec{b}$$此时 $R$ 是上三角方阵, 方程很容易求解.

更一般的, QR 分解可以推广到任意长方形矩阵.

命题 5.5.2 (QR 分解). 设 $A$ 是 $m\times n$ 实矩阵, 这里 $m\ge n$. 则存在 $m$ 阶正交阵 $Q$ 和 $m\times n$ 矩阵 $R=\left[\begin{array}{c}{R}_1\\ 0\end{array}\right]$, 其中 $R_1$ 是对角元非负的 $n$ 阶上三角矩阵, 使得$$A=QR$$

这也可以通过 Gram-Schmidt 正交化证明, 具体细节留作练习.

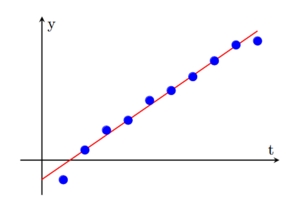
最小二乘法

最小二乘法 (Least Squares Method) 是一种优化方法, 用于拟合数据点并找到最佳的拟合曲线. 其基本目标是通过最小化拟合曲线与数据点之间的误差平方和来找到最佳的参数.

例如我们有一组数据 $(t_i,y_i)$ 如图, 希望用一个线性函数 $y=at+b$ 来拟合这组数据. 即目标是找到 $a,b$ 使得$$\left[\begin{array}{cc}{t}_1& 1\\ t_2& 1\\ ⋮& ⋮\\ t_n& 1\end{array}\right]\left[\begin{array}{c}a\\ b\end{array}\right]=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_n\end{array}\right]$$我们把待求的拟合参数记作未知变量 $\vec{x}=\left[\begin{array}{c}a\\ b\end{array}\right]$, 则上述关系变成求解线性方程组 $A\vec{x}=\vec{y}$.

然而实际上数据不可能严格落在一条直线上, 因此这个线性方程组是没有解的. 退而求其次, 我们可以寻找 $\vec{x}$ 使得如下的平方误差最小$$\underset{\vec{x}}{\min }\Vert A\vec{x}-\vec{y}{\Vert }^2\text{或}\underset{\vec{x}}{\min }\Vert A\vec{x}-\vec{y}\Vert$$从而拟合出一条相对比较符合原始数据的直线.

一般地, 给定 $m\times n$ 实矩阵 $A$ 和向量 $\vec{y}\in {\mathbb{R}}^m$, 求解$$\underset{\vec{x}\in {\mathbb{R}}^n}{\min }\Vert A\vec{x}-\vec{y}\Vert$$这一问题称为最小二乘问题. 这个问题的解 $\vec{x}$ 称为线性方程组 $A\vec{x}=\vec{y}$ 的最小二乘解.

当然如果线性方阵组 $A\vec{x}=\vec{y}$ 本身有解的话, 那么它的解自然是最小二乘解. 这个问题的核心是处理线性方阵组 $A\vec{x}=\vec{y}$ 没有解的情况. 从几何上看, 矩阵 $A$ 定义了一个线性映射$$A:{\mathbb{R}}^n\to {\mathbb{R}}^m$$令 $W\subset {\mathbb{R}}^m$ 是这个映射的象, 即所有形如 $A\vec{x}$ 的向量构成的集合. $W$ 是 ${\mathbb{R}}^m$ 的一个线性子空间. 由命题 5.2.12 我们知道$$\underset{\vec{x}\in {\mathbb{R}}^n}{\min }\Vert A\vec{x}-\vec{y}\Vert =\Vert \vec{y}-p_W(\vec{y})\Vert$$这里 $p_W(\vec{y})$ 是 $\vec{y}$ 向 $W$ 的正交投影. 因此最小二乘问题的解即为线性方程组$$A\vec{x}=p_W(\vec{y})$$的解. 由 $p_W(\vec{y})\in W$, 这个线性方程组的解存在, 其通解的自由参数个数是 $n-\mathrm{rank}A$.

命题 5.5.3. $\vec{x}$ 是线性方程组 $A\vec{x}=\vec{y}$ 的最小二乘解当且仅当$$A^{T}A\vec{x}=A^T\vec{y}$$

证明: 对任意的向量 $\vec{z}\in {\mathbb{R}}^n,\vec{c}\in {\mathbb{R}}^m$, 我们有$$⟨A\vec{z},\vec{c}⟩=(A\vec{z}{)}^T\vec{c}={\vec{z}}^T{A}^T\vec{c}$$故 $\vec{c}\in W^{\perp }$ 当且仅当 $⟨A\vec{z},\vec{c}⟩={\vec{z}}^T{A}^T\vec{c}=0$ 对所有 $\vec{z}$ 成立, 即等价于 $A^T\vec{c}=0$.

$\vec{x}$ 是最小二乘解当且仅当 $A\vec{x}=p_W(\vec{y})$, 即$$A\vec{x}-\vec{y}\in W^{\perp }$$由上述讨论这等价于$$A^T(A\vec{x}-\vec{y})=0\text{即}{A}^{T}A\vec{x}=A^T\vec{y}$$$\square$

注记. 我们也可以通过微积分的方法来证明这个结论. 考虑 $n$ 个变量的函数$$f(\vec{x})=\Vert A\vec{x}-\vec{y}{\Vert }^2$$最小二乘解即为函数 $f$ 的最小值. 另一方面, $$f(\vec{x})=(A\vec{x}-\vec{y}{)}^T(A\vec{x}-\vec{y})={\vec{x}}^T{A}^{T}A\vec{x}-2{\vec{x}}^T{A}^T\vec{y}+{\vec{y}}^T\vec{y}$$

由于 $A^{T}A$ 半正定, 这是一个凸函数, 最小值即为 $f$ 的极值. 求解极值方程$$\frac{\partial f}{\partial x_i}=0\text{即得}{A}^{T}A\vec{x}=A^T\vec{y}$$

由上述命题, 我们可以得到如下求解最小二乘问题的算法. 不妨设 $A$ 的列向量是线性无关的, 此时最小二乘法的解是唯一的. 设 $A$ 的 QR 分解为$$A=QR=Q\left[\begin{array}{c}{R}_1\\ 0\end{array}\right]=\left[\begin{array}{cc}{Q}_1& Q_2\end{array}\right]\left[\begin{array}{c}{R}_1\\ 0\end{array}\right]$$由假设, $R_1$ 是可逆 $n$ 阶上三角矩阵. 代入最小二乘解的方程 $A^{T}A\vec{x}=A^T\vec{y}$, 我们得到$$R_1^T{R}_1\vec{x}=\left[\begin{array}{cc}{R}_1^T& 0\end{array}\right]\left[\begin{array}{c}{Q}_1^T\\ Q_2^T\end{array}\right]\vec{y}=R_1^T{Q}_1^T\vec{y}$$即$$R_1\vec{x}=Q_1^T\vec{y}$$由于 $R_1$ 是上三角方阵, 这个方程组很容易求解.

广义逆

矩阵的广义逆是一种对矩阵的 “逆” 这个概念的推广. 广义逆在矩阵不可逆或者矩阵不是方阵的情况下, 提供了一种类似逆矩阵的替代方法, 广泛应用于求解线性方程组.

定义 5.5.4. 设 $A$ 是 $m\times n$ 矩阵. 如果 $n\times m$ 矩阵 $X$ 满足$$AXA=A$$则称 $X$ 为 $A$ 的一个广义逆.

矩阵的广义逆总是存在的, 而且并不唯一. 我们用符号 $A^{-}$ 来表示 $A$ 的一个广义逆. 我们考虑实矩阵的情况. 对 $A$ 作奇异值分解$$A=U\Sigma V^T$$这里 $U$ 是 $m$ 阶正交阵, $V$ 是 $n$ 阶正交阵. 则$$(U\Sigma V^T)X(U\Sigma V^T)=U\Sigma V^T\text{即}\Sigma V^{T}XU\Sigma =\Sigma$$

代入 $\Sigma =\left[\begin{array}{cc}{\Sigma }_r& 0\\ 0& 0\end{array}\right]$, 这里 ${\Sigma }_r=\mathrm{diag}({\sigma }_1,\cdots ,{\sigma }_r)$$$\left[\begin{array}{cc}{\Sigma }_r& 0\\ 0& 0\end{array}\right]V^{T}XU\left[\begin{array}{cc}{\Sigma }_r& 0\\ 0& 0\end{array}\right]=\left[\begin{array}{cc}{\Sigma }_r& 0\\ 0& 0\end{array}\right]$$得到 $X$ 的通解为$$V^{T}XU=\left[\begin{array}{cc}{\Sigma }_r^{-1}& \ast \\ & \ast \end{array}\right]\text{即}X=V\left[\begin{array}{cc}{\Sigma }_r^{-1}& \ast \\ & \ast \end{array}\right]U^T$$

因此对于 $m\times n$ 矩阵$$A=U\left[\begin{array}{cc}{\Sigma }_r& 0\\ 0& 0\end{array}\right]V^T$$它的广义逆的一般形式为 $m\times n$ 矩阵$$A^{-}=V\left[\begin{array}{cc}{\Sigma }_r^{-1}& \ast \\ & \ast \end{array}\right]U^T$$这里 $\ast$ 是任意数. 这里面有一个特别的广义逆$$V\left[\begin{array}{cc}{\Sigma }_r^{-1}& 0\\ 0& 0\end{array}\right]U^T$$称为 Moore–Penrose 逆. 我们将在 Moore–Penrose 逆 详细讨论 Moore–Penrose 逆的刻画和性质.

命题 5.5.5. 线性方程组 $A\vec{x}=\vec{b}$ 有解的充分必要条件是$$\vec{b}=A{A}^{-}\vec{b}$$这里 $A^{-}$ 是 $A$ 的任意一个广义逆. 此时 $A^{-}\vec{b}$ 是方程的一个特解.

证明: 假设 ${\vec{x}}_0$ 是线性方程组 $A\vec{x}=\vec{b}$ 的解, 则$$\vec{b}=A{\vec{x}}_0=A{A}^{-}A{\vec{x}}_0=A{A}^{-}\vec{b}$$

反之, 假设 $\vec{b}=A{A}^{-}\vec{b}$ 成立. 令 ${\vec{x}}_0=A^{-}\vec{b}$, 则$$A{\vec{x}}_0=A{A}^{-}\vec{b}=\vec{b}\text{成立}$$

$\square$

我们知道, 对于 $n$ 阶可逆方阵 $A$, 线性方阵组 $A\vec{x}=\vec{b}$ 具有唯一解$$\vec{x}=A^{-1}\vec{b}$$对于一般的 $m\times n$ 矩阵 $A$, 广义逆给出了类似的公式: 假设方阵组 $A\vec{x}=\vec{b}$ 有解, 则 $\vec{x}=A^{-}\vec{b}$ 给出了一个具体的解.

命题 5.5.6. $A$ 是 $m\times n$ 矩阵, $A^{-}$ 是 $A$ 的某个取定的广义逆. 则齐次线性方程组 $A\vec{x}=0$ 的通解为$$\vec{x}=(I_n-A^{-}A)\vec{z}$$这里 $\vec{z}$ 是任意 $n$ 维列向量. 特别地, 如果线性方程组 $A\vec{x}=\vec{b}$ 有解, 则它的通解为$$\vec{x}=A^{-}\vec{b}+(I_n-A^{-}A)\vec{z}$$

证明: 由$$A(I_n-A^{-}A)\vec{z}=(A-A{A}^{-}A)\vec{z}=0$$知对任意 $\vec{z}$, $(I_n-A^{-}A)\vec{z}$ 是齐次方程组的解.

设 ${\vec{x}}_0$ 是齐次线性方程组 $A\vec{x}=0$ 的任意一个解, 即 $A{\vec{x}}_0=0$. 取 $\vec{z}={\vec{x}}_0$, 则$${\vec{x}}_0=(I_n-A^{-}A){\vec{x}}_0=(I_n-A^{-}A)\vec{z}$$即 ${\vec{x}}_0$ 可以表达为命题要求形式.

$\square$

如果线性方程组 $A\vec{x}=\vec{b}$ 无解, 我们可以考虑它的最小二乘问题. 设 $A$ 的奇异值分解$$A=U\left[\begin{array}{cc}{\Sigma }_r& 0\\ 0& 0\end{array}\right]V^T$$我们考虑一个特殊的广义逆 (即 Moore–Penrose 逆) $$A^{-}=V\left[\begin{array}{cc}{\Sigma }_r^{-1}& 0\\ 0& 0\end{array}\right]U^T$$

这个广义逆满足$$\begin{array}{rl}{A}^{T}A{A}^{-}=& V\left[\begin{array}{cc}{\Sigma }_r& 0\\ 0& 0\end{array}\right]U^{T}U\left[\begin{array}{cc}{\Sigma }_r& 0\\ 0& 0\end{array}\right]V^{T}V\left[\begin{array}{cc}{\Sigma }_r^{-1}& 0\\ 0& 0\end{array}\right]U^T\\ =& V\left[\begin{array}{cc}{\Sigma }_r& 0\\ 0& 0\end{array}\right]U^T=A^T\end{array}$$即 $A^T(I_m-A{A}^{-})=0$. 考虑 ${\vec{x}}_0=A^{-}\vec{b}$. 对任意向量 $\vec{y}\in {\mathbb{R}}^n$$$\begin{array}{r}⟨A\vec{y},\vec{b}-A{\vec{x}}_0⟩={\vec{y}}^T{A}^T(I_m-A{A}^{-})\vec{b}=0\end{array}$$因此 $A{\vec{x}}_0$ 即为 $\vec{b}$ 向 $A$ 的像的投影. 故 ${\vec{x}}_0=A^{-}\vec{b}$ 给出了一个最小二乘解. 在 Moore–Penrose 逆 节中, 我们将说明在复线性空间中也有类似的结论.

矩阵的谱范数

定义 5.5.7. 设 $A$ 是 $m\times n$ 实矩阵, 其谱范数 $\Vert A\Vert$ 定义为:

$$\Vert A\Vert =\underset{\vec{x}\ne 0}{\max }\frac{\Vert A\vec{x}\Vert }{\Vert \vec{x}\Vert }=\underset{\Vert \vec{x}\Vert =1}{\max }\Vert A\vec{x}\Vert$$其中, $\Vert A\vec{x}\Vert$ 是 ${\mathbb{R}}^m$ 中向量 $A\vec{x}$ 的欧几里得范数, $\Vert \vec{x}\Vert$ 是 ${\mathbb{R}}^n$ 中向量 $\vec{x}$ 的欧几里得范数.

命题 5.5.8. 矩阵的谱范数满足如下基本性质:

1.	非负性: $\Vert A\Vert \ge 0$, 且 $\Vert A\Vert =0⟺A=0$
2.	齐次性: 对任意 $\alpha \in \mathbb{R}$, $\Vert \alpha A\Vert =|\alpha |\Vert A\Vert$
3.	三角不等式: $\Vert A+B\Vert \le \Vert A\Vert +\Vert B\Vert$
4.	乘积性质: $\Vert AB\Vert \le \Vert A\Vert \Vert B\Vert$
5.	若 $U,V$ 是正交方阵, 则 $\Vert UA{V}^T\Vert =\Vert A\Vert$

证明: 我们证明最后一条性质, 其他留作练习. 由于正交方阵保持欧几里得范数, 我们有$$\begin{array}{r}\Vert UA{V}^T\Vert =\underset{\vec{x}\ne 0}{\max }\frac{\Vert UA{V}^T\vec{x}\Vert }{\Vert \vec{x}\Vert }=\underset{\vec{x}\ne 0}{\max }\frac{\Vert A{V}^T\vec{x}\Vert }{\Vert V^T\vec{x}\Vert }\stackrel{\vec{y}=V^T\vec{x}}{=}\underset{\vec{y}\ne 0}{\max }\frac{\Vert A\vec{y}\Vert }{\Vert \vec{y}\Vert }=\Vert A\Vert \end{array}$$

$\square$

命题 5.5.9. 矩阵的谱范数 $\Vert A\Vert$ 等于 $A$ 的最大奇异值.

证明: 设 $A$ 的奇异值分解为 $A=U\Sigma V^T$, 则 $\Vert A\Vert =\Vert \Sigma \Vert$. 由$$\Sigma =\left[\begin{array}{cc}\left[\begin{array}{cccc}{\sigma }_1& 0& \cdots & 0\\ 0& {\sigma }_2& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots \\ 0& \cdots & 0& {\sigma }_r\end{array}\right]& 0\\ 0& 0\end{array}\right]$$得知$$\begin{array}{r}\Vert \Sigma \Vert =\underset{\vec{x}\ne 0}{\max }\frac{\Vert A\vec{x}\Vert }{\Vert \vec{x}\Vert }=\underset{\vec{x}\ne 0}{\max }\frac{\sqrt{{\sigma }_1^2{x}_1^2+\cdots +{\sigma }_r^2{x}_r^2}}{\sqrt{x_1^2+\cdots +x_n^2}}=\underset{1\le i\le r}{\max }{\sigma }_i\end{array}$$

$\square$

这个命题给出了最大奇异值的几何解释, 即线性映射$$A:{\mathbb{R}}^n\to {\mathbb{R}}^m$$把向量长度伸缩最大的倍数. 我们下面说明, 其他奇异值均有类似的几何解释.

例子 5.5.10. 考虑一个 $n$ 阶实对称方阵 $S$. 由命题 5.4.5, 存在一组标准正交基 ${\vec{\beta }}_1,\cdots ,{\vec{\beta }}_n$ 使得每个 ${\vec{\beta }}_i$ 都是 $S$ 的特征向量. 不妨设其对应的特征值 ${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_n$.

对任意向量 $\vec{x}\in {\mathbb{R}}^n$, 在这组基下的线性表达为$$\vec{x}=c_1{\vec{\beta }}_1+\cdots +c_n{\vec{\beta }}_n$$由此可得$$\frac{{\vec{x}}^{T}S\vec{x}}{{\vec{x}}^T\vec{x}}=\frac{{\lambda }_1{c}_1^2+\cdots +{\lambda }_n{c}_n^2}{c_1^2+\cdots +c_n^2}$$

易知$${\lambda }_1=\underset{\vec{x}\ne 0}{\max }\frac{{\vec{x}}^{T}S\vec{x}}{{\vec{x}}^T\vec{x}}$$类似的, 我们有$${\lambda }_i=\underset{\begin{array}{c}\vec{x}\ne 0\\ \vec{x}\in \mathrm{Span}\{{\vec{\beta }}_i,\cdots ,{\vec{\beta }}_n\}\end{array}}{\max }\frac{{\vec{x}}^{T}S\vec{x}}{{\vec{x}}^T\vec{x}}=\underset{\begin{array}{c}\vec{x}\ne 0\\ \vec{x}\in \mathrm{Span}\{{\vec{\beta }}_1,\cdots ,{\vec{\beta }}_{i-1}{\}}^{\perp }\end{array}}{\max }\frac{{\vec{x}}^{T}S\vec{x}}{{\vec{x}}^T\vec{x}}$$

设 $A$ 是 $m\times n$ 实矩阵. 我们把上述例子中的方法应用到半正定实对称方阵 $S=A^{T}A$. 设 $A$ 的奇异值为 ${\sigma }_1\ge {\sigma }_2\ge \cdots \ge {\sigma }_r>0$, 即 $A^{T}A$ 的非零特征值为 ${\sigma }_1^2\ge {\sigma }_2^2\ge \cdots \ge {\sigma }_r^2$. 设 ${\vec{\beta }}_1,\cdots ,{\vec{\beta }}_r$ 是 ${\mathbb{R}}^n$ 的标准正交基并且构成 $A^{T}A$ 的特征向量$$A^{T}A{\vec{\beta }}_i=\{\begin{array}{ll}{\sigma }_i^2{\vec{\beta }}_i& 1\le i\le r\\ 0& i>r\end{array}$$

则我们有$${\sigma }_1=\sqrt{\underset{\vec{x}\ne 0}{\max }\frac{{\vec{x}}^T{A}^{T}A\vec{x}}{{\vec{x}}^T\vec{x}}}=\underset{\vec{x}\ne 0}{\max }\frac{\Vert A\vec{x}\Vert }{\Vert \vec{x}\Vert }$$并且 ${\vec{\beta }}_1$ 达到这个最大值$${\sigma }_1=\frac{\Vert A{\vec{\beta }}_1\Vert }{\Vert {\vec{\beta }}_1\Vert }$$

然后考虑 ${\vec{\beta }}_1$ 的正交补空间, 得到次大的奇异值$${\sigma }_2=\sqrt{\underset{\begin{array}{c}\vec{x}\ne 0\\ \vec{x}\in \mathrm{Span}\{{\vec{\beta }}_1{\}}^{\perp }\end{array}}{\max }\frac{{\vec{x}}^T{A}^{T}A\vec{x}}{{\vec{x}}^T\vec{x}}}=\underset{\begin{array}{c}\vec{x}\ne 0\\ \vec{x}\in \mathrm{Span}\{{\vec{\beta }}_1{\}}^{\perp }\end{array}}{\max }\frac{\Vert A\vec{x}\Vert }{\Vert \vec{x}\Vert }$$这样我们依次得到第 $i$ 个奇异值的几何解释$${\sigma }_i=\underset{\begin{array}{c}\vec{x}\ne 0\\ \vec{x}\in \mathrm{Span}\{{\vec{\beta }}_1,\cdots ,{\vec{\beta }}_{i-1}{\}}^{\perp }\end{array}}{\max }\frac{\Vert A\vec{x}\Vert }{\Vert \vec{x}\Vert }$$

图 1. 蓝色和绿色表示奇异值方向, 黑色表示特征值方向

矩阵极限

矩阵的谱范数给出了一个描述矩阵之间 “距离” 的方法.

定义 5.5.11. 我们称一组 $m\times n$ 矩阵 $A_k$ 收敛于 $m\times n$ 矩阵 $B$, 如果$$\underset{k\to \infty }{\lim }\Vert A_k-B\Vert =0$$此时我们记$$\underset{k\to \infty }{\lim }{A}_k=B$$

命题 5.5.12. 设 $A=(a_{ij})$ 是 $m\times n$ 实矩阵. 则$$\underset{i,j}{\max }|a_{ij}|\le \Vert A\Vert \le \sum _{i,j}|a_{ij}|$$

证明: 设$$A=\left[\begin{array}{c}{{\vec{u}}_1}^T\\ ⋮\\ {{\vec{u}}_m}^T\end{array}\right]\text{这里}{\vec{u}}_k=\left[\begin{array}{c}{a}_{k1}\\ ⋮\\ a_{kn}\end{array}\right]\in {\mathbb{R}}^n$$

对任意 $\vec{x}\in {\mathbb{R}}^n$ 且 $\Vert \vec{x}\Vert =1$, 我们有$$A\vec{x}=\left[\begin{array}{c}{{\vec{u}}_1}^T\cdot \vec{x}\\ ⋮\\ {{\vec{u}}_m}^T\cdot \vec{x}\end{array}\right]=\left[\begin{array}{c}⟨{\vec{u}}_1,\vec{x}⟩\\ ⋮\\ ⟨{\vec{u}}_m,\vec{x}⟩\end{array}\right]$$由 Cauchy–Schwarz 不等式, $$\begin{array}{r}\Vert A\vec{x}\Vert \le \sum _i|⟨{\vec{u}}_i,\vec{x}⟩|\le \sum _i\Vert {\vec{u}}_i\Vert \Vert \vec{x}\Vert =\sum _i\Vert {\vec{u}}_i\Vert \le \sum _i\sum _j|a_{ij}|\end{array}$$

另一方面, 考虑 ${\mathbb{R}}^n$ 中的标准基 ${\vec{e}}_j$. 由$$A{\vec{e}}_j=\left[\begin{array}{c}{a}_{1j}\\ ⋮\\ a_{nj}\end{array}\right]$$因此对任意指标 $i,j$$$\Vert A\Vert \ge \Vert A{\vec{e}}_j\Vert \ge |a_{ij}|$$命题得证.

$\square$

这个命题说明, 矩阵极限成立$$\underset{k\to \infty }{\lim }{A}_k=B$$当且仅当 $A_k$ 的每个矩阵元都收敛到 $B$ 中对应的矩阵元.

作为一个应用, 我们考虑 $n$ 阶实方阵 $A$. 由矩阵范数的乘积性质, 我们有$$\Vert \frac{A^n}{n!}\Vert \le \frac{\Vert A{\Vert }^n}{n!}$$由于级数$$\sum _{n=0}^{\infty }\frac{\Vert A{\Vert }^n}{n!}=e^{\Vert A\Vert }$$收敛, 上述谱范数的估计可以证明矩阵级数$$\underset{N\to \infty }{\lim }\sum _{k=0}^N\frac{A^k}{k!}$$收敛. 我们把这个极限矩阵方便地记为 $e^A$$$e^A:=\sum _{k=0}^{\infty }\frac{A^k}{k!}$$

并且

$$\Vert e^A\Vert =\Vert \sum _{k=0}^{\infty }\frac{A^k}{k!}\Vert \le \sum _{k=0}^{\infty }\Vert \frac{A^k}{k!}\Vert \le \sum _{k=0}^{\infty }\frac{\Vert A{\Vert }^k}{k!}=e^{\Vert A\Vert }$$由如上级数公式容易证明, $e^A$ 是可逆矩阵, 并且它的逆是 $e^{-A}$. 即$$e^A{e}^{-A}=I_n$$指数矩阵 $e^A$ 具有和指数函数 $e^x$ 非常类似的性质.

命题 5.5.13. 设 $A,B$ 是两个相互交换的 $n$ 阶方阵, 即满足 $AB=BA$. 则$$e^A{e}^B=e^{A+B}$$

证明: $$\begin{array}{rl}{e}^{A+B}=& \sum _{n=0}^{\infty }\frac{(A+B{)}^n}{n!}\\ \stackrel{\text{利用}}{\underset{\text{AB=BA}}{=}}& \sum _{n=0}^{\infty }\frac{1}{n!}\sum _{k=0}^n\left(\genfrac{}{}{0ex}{}{n}{k}\right)A^k{B}^{n-k}\\ =& \sum _{n=0}^{\infty }\sum _{k+m=n}\frac{A^k{B}^m}{k!m!}\\ =& \left(\sum _{k=0}^{\infty }\frac{A^k}{k!}\right)\left(\sum _{m=0}^{\infty }\frac{B^m}{m!}\right)=e^A{e}^B\end{array}$$

$\square$

注记. 两个方阵如果不交换, $AB\ne BA$, 则有如下的 Baker-Campbell-Hausdorff 公式$$e^A\cdot e^B=e^{A+B+\frac{1}{2}[A,B]+\frac{1}{12}[A,[A,B]]-\frac{1}{12}[B,[A,B]]+\cdots }$$

微分方程中的应用

现在我们引入一个变量 $t$, 考虑随 $t$ 变化的矩阵$$e^{tA}=\sum _{k=0}^{\infty }\frac{t^k{A}^k}{k!}$$对矩阵等式$$\frac{d}{dt}\left(\frac{t^k{A}^k}{k!}\right)=\frac{t^{k-1}{A}^k}{(k-1)!}.$$求和, 可以得到

$$\frac{d}{dt}{e}^{tA}=A{e}^{tA}$$

对任意向量 ${\vec{y}}_0\in {\mathbb{R}}^n$, 考虑如下向量函数$$\vec{y}(t)=e^{tA}{\vec{y}}_0$$由上述讨论知$$\frac{d\vec{y}}{dt}=A{e}^{tA}{\vec{y}}_0=A\vec{y}$$并且在 $t=0$ 时有 $\vec{y}(0)=\overrightarrow{y_0}$. 因此 $\vec{y}(t)=e^{tA}{\vec{y}}_0$ 给出了如下齐次线性常微分初值问题的解$$\{\begin{array}{l}\frac{d\vec{y}}{dt}=A\vec{y}\\ \vec{y}(0)={\vec{y}}_0\end{array}$$

进一步, 我们可以考虑非齐次线性常微分方程组$$\{\begin{array}{l}\frac{d\vec{y}}{dt}=A\vec{y}+\vec{b}(t)\\ \vec{y}(0)={\vec{y}}_0\end{array}$$这里 $\vec{b}(t)=\left[\begin{array}{c}{b}_1(t)\\ ⋮\\ b_n(t)\end{array}\right]$ 是随时间变化的向量. 上述方程等价于$$\frac{d}{dt}(e^{-tA}\vec{y})=e^{-tA}\vec{b}(t)$$两边积分, 我们得到$$e^{-tA}\vec{y}-{\vec{y}}_0={\int }_0^t{e}^{-sA}\vec{b}(s)ds$$

因此$$\vec{y}=e^{tA}{\vec{y}}_0+{\int }_0^t{e}^{(t-s)A}\vec{b}(s)ds$$给出了非齐次线性常微分方程组$$\{\begin{array}{l}\frac{d\vec{y}}{dt}=A\vec{y}+\vec{b}(t)\\ \vec{y}(0)={\vec{y}}_0\end{array}$$的解.