1. 问题模型

1.1物理场景

限制性三体问题 (restricted three-body problem, R3BP) 是经典的天体力学模型, 可以用来描述许多现实存在的天体系统. 在这个问题里, 有两个质量很大的质点 $m_0,m_1$ 和一个质量很小的质点 $m_2$. R3BP 就是将 $m_2$ 视作 " 试验质点 ", 求解它在 $m_0$ 和 $m_1$ 的引力场中的运动, 而忽略它对两个大质点的作用.

Poincaré 在研究此问题时, 作出了一个著名的论断: 即便在 $m_0=m_1$ 这种简单的情形之下, 如果 $m_2$ 的速度接近逃逸速度, 那么它的运动仍旧有可能非常混乱. 他的研究事实上开启了现代动力系统理论, 也提供了混沌系统 (chaotic system) 最初的例子.

然而 Poincaré 的结论其实远远不能覆盖 R3BP 的所有令人感兴趣的情形. 现实中存在的恒星系已经可以提供许多这样的例子: 如果有一颗气态巨行星 – 例如木星 – 和若干质量极小的小行星围着恒星公转, 那么木星对这些小行星的引力摄动似乎并不会立刻破坏它们的轨道, 虽然长期来讲似乎确有这种可能.

这显然远非 Poincaré 所讨论的情形. 例如, 在太阳系中, 小行星带的半径大致为 2AU, 木星的轨道半径大致为 5AU, 而由于木星的质量仅为太阳的千分之一, 所以简单的计算立刻表明, 木星对小行星的引力相较于太阳而言是一个很小的微扰. 但 Poincaré 的结论却提示我们, 即便是一个很简单的系统的微扰, 它的稳定性也远非显而易见. 有没有什么机制能确保这种稳定性呢?

这类问题可以大致化归为平面圆型限制三体问题 (restricted circular planar three body problem, RCP3BP). 在 RCP3BP 中, 我们作出下列假定:

假定 1.1.1.

1.	质点 $m_0$ (" 恒星 ") 具有远大于 $m_1$ 和 $m_2$ 的质量;
2.	质点 $m_1\ll m_0$ (" 巨行星 ") 在 $m_0$ 的引力作用下绕它作匀速圆周运动;
3.	质点 $m_2$ (" 小行星 ") 的运动与 $m_0,m_1$ 处于同一平面 (" 黄道面 ") 内;
4.	质点 $m_2$ 受到 $m_0$ 的引力作用, 同时受到 $m_1$ 的引力摄动, 但 $m_2\ll m_1$, 所以它对 $m_0,m_1$ 的反作用被忽略;
5.	为了方便起见, 选择自然单位制, 并设总质量 $m_0+m_1=1$.

唯一需要稍微解释的是假定 3, 但这样假定的合理性可以立即从下文中看出来.

1.2运动方程

在惯性参照系下, 设三个质点在空间中的位置分别是 ${\mathbf{u}}_0,{\mathbf{u}}_1,{\mathbf{u}}_2$. 则 RCP3BP 的运动方程就是$$\begin{array}{rl}{\mathbf{u}}_0^{\prime \prime }& =-\frac{m_1({\mathbf{u}}_0-{\mathbf{u}}_1)}{|{\mathbf{u}}_0-{\mathbf{u}}_1{|}^3},\\ {\mathbf{u}}_1^{\prime \prime }& =-\frac{m_0({\mathbf{u}}_1-{\mathbf{u}}_0)}{|{\mathbf{u}}_0-{\mathbf{u}}_1{|}^3},\\ {\mathbf{u}}_2^{\prime \prime }& =-\frac{m_0({\mathbf{u}}_2-{\mathbf{u}}_0)}{|{\mathbf{u}}_2-{\mathbf{u}}_0{|}^3}-\frac{m_1({\mathbf{u}}_2-{\mathbf{u}}_1)}{|{\mathbf{u}}_2-{\mathbf{u}}_1{|}^3}.\end{array}$$(1.1)

比起一般的三体问题, 这当然是简化了很多的:

•	${\mathbf{u}}_0(t)$ 和 ${\mathbf{u}}_1(t)$ 满足的方程组不过是 Kepler 轨道的运动方程, 因此它们都可以明确地解出来, 而 ${\mathbf{u}}_2(t)$ 满足的方程因此就成了一个周期受迫振动方程;
•	如果 $m_1=0$, 那么 ${\mathbf{u}}_0(t)$ 和 ${\mathbf{u}}_2(t)$ 满足的不过是另一个 Kepler 轨道的运动方程, 由此可见 (1.1) 实为两个解耦的 Kepler 轨道的摄动, 摄动参数是 " 巨行星 " 的质量 $m_1$.

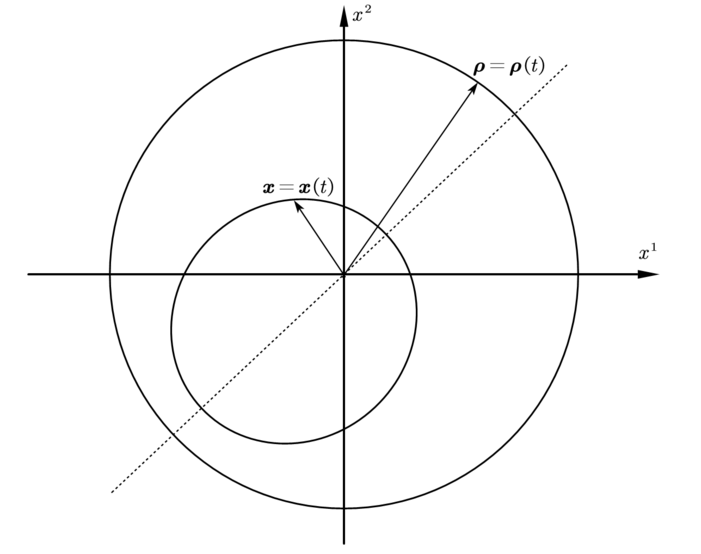
我们可以把 (1.1) 进一步化简. 引入新的向径$$\mathbf{\rho }={\mathbf{u}}_1-{\mathbf{u}}_0,\mathbf{x}={\mathbf{u}}_2-{\mathbf{u}}_0,$$它们是以 " 太阳 " $m_0$ 为参考系时测得的坐标. 这就把运动方程化成了 " 小行星 " 在日心系下的位置向量 $\mathbf{x}$ 这一个未知量的方程:$${\mathbf{x}}^{\prime \prime }=-m_0\frac{\mathbf{x}}{|\mathbf{x}{|}^3}-m_1\frac{\mathbf{\rho }}{|\mathbf{\rho }{|}^3}-m_1\frac{\mathbf{x}-\mathbf{\rho }}{|\mathbf{x}-\mathbf{\rho }{|}^3},$$(1.2)其中 $\mathbf{\rho }(t)$ 满足$${\mathbf{\rho }}^{\prime \prime }=-\frac{\mathbf{\rho }}{|\mathbf{\rho }{|}^3}.$$根据假定, 我们选取匀速圆周运动作为它的特解: $\mathbf{\rho }(t)=(\cos t,\sin t)$. 由此可以更明显地看出包含 $m_1$ 的后两项是扰动项: 如果 $m_1=0$, 则 (1.2) 不过又是单个质点引力场中的运动方程. 另外, (1.2) 显然说明如果 $\mathbf{x}$ 的初始位置和初始速度都在 $\mathbf{\rho }(t)$ 所在的平面内, 那么 $\mathbf{x}$ 将一直在这个平面内.

下图给出了系统在 $m_1=0$ 时构型空间中的轨道: 这是两个相互解耦的 Kepler 轨道, “恒星” $m_0$ 位于圆锥曲线的焦点处.

1.3Hamilton 系统

(1.2) 更可化为含时的 Hamilton 方程组, 含时的 Hamilton 函数是$$H(\mathbf{x},\mathbf{p},t)=\frac{|\mathbf{p}{|}^2}{2}-\frac{m_0}{|\mathbf{x}|}+m_1\mathbf{x}\cdot \mathbf{\rho }(t)-\frac{m_1}{|\mathbf{x}-\mathbf{\rho }(t)|}.$$为方便起见, 可以想办法把它化成自治的 Hamilton 函数. 为此只需要引入 $\tau =t$ 以及与它共轭的正则变量 $T$, 并写$$H_1(\mathbf{x},\mathbf{p},\tau ,T)=\frac{|\mathbf{p}{|}^2}{2}-\frac{m_0}{|\mathbf{x}|}+T+m_1\mathbf{x}\cdot \mathbf{\rho }(\tau )-\frac{m_1}{|\mathbf{x}-\mathbf{\rho }(\tau )|}$$(1.3)就可以了.

(1.3) 就是我们感兴趣的 Hamilton 函数. 一眼可见, 它是一个简单的 Hamilton 函数的扰动. 当 $m_1=0$ 时, 相应的 Hamilton 方程组给出 Kepler 轨道.

于是, 我们关心的问题如下:

问题 1.3.1. 如果 $m_1\ll 1$, 那么扰动的 Hamilton 函数 (1.3) 的相流是否还有比较规整的轨线?

对于现实中的太阳-木星-小行星系统来说, 在给定的单位之下, $m_1$ 大致是 $10^{-3}{m}_0\simeq 10^{-3}$, 一个典型的小行星的轨道半径 $|\mathbf{x}|\simeq |\mathbf{\rho }|/2\simeq 0.5$. 由此可见, 对于小行星的运动来说, (1.3) 的后两项代表木星引起的引力摄动, 它比起太阳的影响来讲确实是微扰.

当然, 它跟现实场景仍然有所偏差:

•	木星轨道并不是正圆, 但它的离心率只有 0.05;
•	小行星的黄道面和木星的黄道面并不一样, 但两者的夹角往往也并不很大;
•	如果小行星的形状很不规则, 而且有自转, 那么把它视为质点也是过度简化的假定.

不过, 从 (1.3) 的表达式来看, 其实最大的误差还是来自于忽略木星轨道自身的离心率. 所以, 这个模型总的来说还是基本合理的.