2. Delaunay 坐标

2.1Liouville-Arnold 定理

Hamilton 函数 (1.3) 仍然不是很方便实际操作. 即便没有微扰, Kepler 轨道的 Hamilton 函数$$H_0(\mathbf{x},\mathbf{p})=\frac{|\mathbf{p}{|}^2}{2}-\frac{m_0}{|\mathbf{x}|},(\mathbf{x},\mathbf{p})\in {\mathbb{R}}^2\setminus \{0\}\times {\mathbb{R}}^2$$(2.1)本身也并不能立刻让人看出它的可积性. 为了展示它的可积性, 需要引入作用-角变量 (action-angle variable). 在单个质点引力场的情形, 这特别被称为 Delaunay 坐标. 粗略地说, 只要系统有足够多的首次积分, 那么就可以构造作用-角变量.

在辛几何中, 经典的 Liouville-Arnold 定理说明的正是这件事:

定理 2.1.1. 设 $(M^{2n},\omega )$ 是辛流形. 假定存在 $n$ 个实值函数 $f_1,f_2,\cdots ,f_n:M\to \mathbb{R}$, 使得

•	诸 Hamilton 向量场 $X_{f_i}$ 在每一点都线性无关;
•	诸 Hamilton 向量场 $X_{f_i}$ 相互对易;
•	对于 $c\in {\mathbb{R}}^n$, 水平集 $L_c:=\{(f_1,f_2,\cdots ,f_n)=c\}$ 是连通的紧子流形.

那么每一个 $L_c$ 实际上都微分同胚于 $n$ 维环面 ${\mathbb{T}}^n$. 进一步地, 每一个 $L_c$ 都有邻域 $U$, 其上有辛微分同胚$$({\theta }_1,{\theta }_2,\cdots ,{\theta }_n,I_1,I_2,\cdots ,I_n):M\to {\mathbb{T}}^n\times \Omega \subset {\mathbb{T}}^n\times {\mathbb{R}}^n,$$使得 $\omega ={\sum }_{i=1}^{n}d{\theta }_i\wedge d{I}_i$, 而且每个 $f_i$ 都只是 $I_1,I_2,\cdots ,I_n$ 的函数.

这个局部坐标 $(\theta ,I)$ 就是作用-角变量. 定理的证明可以参考任何标准的辛几何教材. 我们可以大致勾勒一下证明的思路:

证明大意. 既然诸 Hamilton 向量场 $X_{f_i}$ 线性无关且相互对易, 可见每个 $L_c$ 都是 $n$ 维分布 $\{X_{f_i}{\}}_{i=1}^n$ 的极大积分子流形, 而且加法群 $({\mathbb{R}}^n,+)$ 按照如下方式作用在每个 $L_c$ 上: 设 ${\Phi }_i^t$ 是向量场 $X_{f_i}$ 的流, 则定义$$(t_1,\cdots ,t_n)\circ x:=({\Phi }_1^{t_1}\circ \cdots \circ {\Phi }_n^{t_n})(x).$$这些流相互对易, 所以的确给出了 $({\mathbb{R}}^n,+)$ 的作用. 利用 $L_c$ 的连通性和紧性, 可以证明每一个 $x\in L_c$ 的稳定子群实际上都是同一个, 且必定同构于 ${\mathbb{Z}}^n$. 所以 $L_c$ 只能微分同胚于环面 ${\mathbb{T}}^n$.

如果 $(t_1^0(c),\cdots ,t_n^0(c))$ 是 $x_0\in L_c$ 的稳定子群 $G_c$ 的生成元, 那么同一个水平集上的 $x$ 的角坐标就定义为$${\theta }_i(x)=\frac{2\pi t_i}{t_i^0(c)}\mathrm{mod}2\pi ,$$其中 $(t_1,\cdots ,t_n)$ 使得$$x=({\Phi }_1^{t_1}\circ \cdots \circ {\Phi }_n^{t_n})(x_0).$$与 ${\theta }_i$ 共轭的作用量坐标则是$$I_i={\int }_{{\gamma }_i}\alpha ,$$其中 ${\gamma }_i$ 是环面 $L_c\cong {\mathbb{T}}^n$ 第一奇异同调群的第 $i$ 个生成元, 而 $\alpha$ 是典则 1-形式 (即 $d\alpha$ 恰好等于辛形式 $\omega$). 由于 $d\alpha =\omega$, 而 $\omega$ 拖回到 $L_c$ 上等于零, 所以 $I_i$ 的定义并不依赖于 ${\gamma }_i$ 的代表元的选取.

$\square$

这个证明实际上也给出了计算作用-角变量 $(I,\theta )$ 的方法. 如果取一个局部 Darboux 坐标 $(q,p)$, 那么$$I_i={\int }_{{\gamma }_i}\sum _{j=1}^n{p}_{i}d{q}_i,$$而角变量

2.2Delaunay 坐标与轨道根数

回到没有摄动的 Hamilton 函数 (2.1). 显然这是一个中心对称的 Hamilton 函数, 所以在构型空间中换成极坐标会方便一些. 回忆一下, 如果 $(q,p)$ 是局部 Darboux 坐标, 而 $\chi (q)$ 是微分同胚, 那么$$\left(\begin{array}{c}q\\ p\end{array}\right)\to \left(\begin{array}{c}\chi (q)\\ {\chi }^{\prime }(q{)}^{-\mathsf{T}}p\end{array}\right)$$是辛微分同胚. 于是, 在极坐标替换之下, $$\left(\begin{array}{c}{x}^1\\ x^2\\ p_1\\ p_2\end{array}\right)={\varphi }_{\text{pc}}\left(\begin{array}{c}r\cos \phi \\ r\sin \phi \\ R\cos \phi -\Phi \sin \phi /r\\ R\sin \phi +\Phi \cos \phi /r\end{array}\right)$$就给出了一个从极坐标 $r,\phi ,R,\Phi$ 到直角坐标 $\mathbf{x},\mathbf{p}$ 的辛变换, 在极坐标下辛形式仍旧是$$d\phi \wedge d\Phi +dr\wedge dR.$$Hamilton 函数 (2.1) 变为$$H_{\mathrm{pc}}(r,\phi ,R,\Phi )=(H_0\circ {\varphi }_{\text{pc}})(r,\phi ,R,\Phi )=\frac{1}{2}\left(R^2+\frac{{\Phi }^2}{r^2}\right)-\frac{m_0}{r}.$$这里 pc 是 polar coordinate 的缩写.

显而易见, $\Phi$ 是一个守恒量, 因为 Hamilton 函数不含 $\phi$. $\Phi$ 实际上正比于质点 $m_2$ 运动的角动量 (的垂直分量). 因此我们已经找到了一个首次积分. Hamilton 函数 $H_{\text{pc}}$ 本身显然可以取为第二个首次积分. 因此, 根据 Liouville-Arnold 定理, 这个双自由度的 Hamilton 系统是完全可积的.

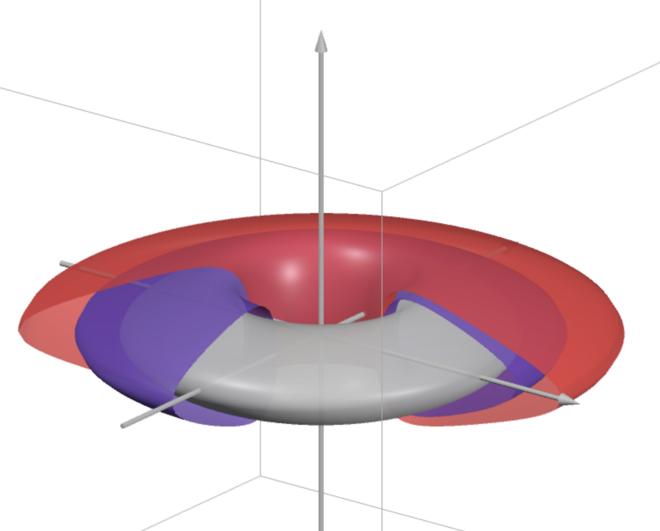
我们更可以直接算出第二个作用量变量 $I$. 系统的不变环面是 $\Phi =\text{const}.,H_{\text{pc}}=\text{const}.$. 下图给出了 $\Phi =1$ 时 $E=-0.3$ 至 $E=-0.4$ 对应的环面在 $R,x^1,x^2$ 空间中的形状.

不变环面的第一同调群的第二个生成元可以取为闭曲线$$\Phi =\text{const}.,H_{\text{pc}}=E,\phi =\text{const}.$$当然, 必须在 $E_{\min }<E<0$ 时这才是闭曲线 (对应于椭圆形的 Kepler 轨道).

因此, 作用量变量 $I$ 就是典则形式 $-\Phi d\phi -Rdr$ 沿着这条曲线的积分 (除以 $2\pi$): $$\begin{array}{rl}I& =\frac{1}{\pi }{\int }_{r_{-}(E,\Phi )}^{r_{+}(E,\Phi )}\sqrt{2E+\frac{2m_0}{r}-\frac{{\Phi }^2}{r^2}}dr\\ & =\frac{m_0}{\sqrt{-E}}-\Phi ,\end{array}$$这里 $r_{\pm }(E,\Phi )$ 是曲线与 $r$ 轴的交点.

2.3RCP3BP 作为摄动问题

最终, 扰动的 Hamilton 函数 (1.3) 化成了$$H(\ell ,g,L,G)=-\frac{1}{2L^2}-G+\epsilon F_{\epsilon }(\ell ,g,L,G).$$(2.2)如果没有摄动 ($m_1=0$), 那么质点 $m_2$ 的 Hamilton 方程是$$L^{\prime }=G^{\prime }=0,{\ell }^{\prime }=\frac{1}{L^3},g^{\prime }=-1,$$因此实际上 $L=L(0)$, $G=G(0)$, 平近点角 $\ell (t)=\ell (0)+t/L(0{)}^3$, 而夹角 $g(t)=g(0)-t$. 但鉴于近心点幅角 $\gamma =g+\tau$, 可见近心点幅角实为常数. 因此, 在没有摄动的情况下, 轨道在构型空间中是一个不动的椭圆, 而平近点角和夹角 $g$ 都随着时间匀速增加. 从相空间的角度来看, Hamilton 流锚定在了不变环面 $L=L(0),G=G(0)$ 上, 在这个环面上则是拟周期转动. 这跟我们已知的结果是吻合的.

于是, 我们终于可以真正把 RCP3BP 作为数学问题提出如下:

问题 2.3.1. 如果 $m_1>0$ 但远小于 1, 那么 Hamilton 函数 $H(\ell ,g,L,G)$ 的相流还有不变环面吗?

在这种情况下, 质点 $m_2$ 在构型空间中的运动轨迹可以近似看作缓慢转动的椭圆. 只不过 " 平近点角 " 和 " 近心点幅角 " 也只能在这个近似意义下理解了.