3. 单纯集

单纯集 (simplicial set) 是一种组合对象, 应用于数学的很多分支, 特别是同伦理论中. 这一节中, 我们介绍单纯集的概念, 并解释如何以之为模型, 来定义无穷范畴.

定义和例子

在定义单纯集之前, 我们先举几个例子, 以建立其直观.

例 3.1. 设 $X$ 是单纯复形 (也就是拓扑中定义单纯同调时考虑的复形), 其中每个单形 $\sigma$ 的顶点都带有一个排序, 使得 $\sigma$ 的每个面含入 $\sigma$ 的映射都保持顶点的排序. 记 $X_n$ 为 $X$ 的所有 $n$ 维单形 (可能退化) 的集合. 则有一列映射其中

•	每个 $X_n$ 有 $(n+1)$ 个到 $X_{n-1}$ 的映射, 分别由取 $n$ 维单形的 $(n+1)$ 个面给出, 称为面映射 (face map).
•	每个 $X_n$ 有 $(n+1)$ 个到 $X_{n+1}$ 的映射, 由 $(n+1)$ 种将 $n$ 维单形视为退化的 $(n+1)$ 维单形的方法给出, 称为退化映射 (degeneracy map).

这一结构就称为单纯集, 细节见下文.

例 3.2. 设 $X$ 是拓扑空间, 记$$\mathrm{Sing}(X{)}_n=\mathsf{T}\mathsf{o}\mathsf{p}({\Delta }^n,X),$$其中 ${\Delta }^n$ 表示拓扑中的标准 $n$ 维单形. 这就给出了单纯集 $\mathrm{Sing}(X)$, 它也具有前一个例子所述的结构. 我们回忆, 奇异同调和奇异上同调都是利用这个单纯集来定义的.

下面, 我们写下单纯集的严格定义.

定义 3.3. 标准单形范畴是如下定义的范畴 $\mathbb{\Delta }$:

•	其对象为所有形如 $[n]=\{0,\dots ,n\}$ 的集合, 其中 $n\ge 0$.
•	态射集 $\mathbb{\Delta }([m],[n])$ 由所有从 $[m]$ 到 $[n]$ 的保序映射 (即保持 $\le$ 关系的映射) 构成.

范畴 $\mathbb{\Delta }$ 也可以看成 (例 3.1 意义下) 带顶点排序的标准单形构成的范畴, 其态射为单形之间将顶点映到顶点的线性映射, 并要求保持顶点的排序.

在范畴 $\mathbb{\Delta }$ 中, 有两类特殊的态射:

•	有面映射$$d^i:[n-1]\to [n](0\le i\le n),$$定义为跳过 $[n]$ 的元素 $i$, 在其余元素上是保序双射.
•	有退化映射$$s^i:[n+1]\to [n](0\le i\le n),$$定义为将 $[n+1]$ 的元素 $i$ 和 $i+1$ 都映到 $[n]$ 的元素 $i$, 在其余元素上是保序双射.

面映射和退化映射构成了 $\mathbb{\Delta }$ 中 (不交换的) 图表不难验证, $\mathbb{\Delta }$ 中所有态射都能写成一系列面映射和退化映射的复合.

定义 3.4. 单纯集 (simplicial set) 是从 ${\mathbb{\Delta }}^{\mathrm{o}\mathrm{p}}$ 到 $\mathsf{S}\mathsf{e}\mathsf{t}$ 的函子, 即从 $\mathbb{\Delta }$ 到 $\mathsf{S}\mathsf{e}\mathsf{t}$ 的反变函子, 也即 $\mathbb{\Delta }$ 上的预层. 单纯集的范畴记为$$\mathsf{s}\mathsf{S}\mathsf{e}\mathsf{t}=\mathsf{F}\mathsf{u}\mathsf{n}({\mathbb{\Delta }}^{\mathrm{o}\mathrm{p}},\mathsf{S}\mathsf{e}\mathsf{t}).$$

更一般地, 对任何范畴 $\mathsf{C}$, 定义

•	$\mathsf{C}$ 中的单纯对象 (simplicial object) 为 ${\mathbb{\Delta }}^{\mathrm{o}\mathrm{p}}$ 到 $\mathsf{C}$ 的函子.
•	$\mathsf{C}$ 中的余单纯对象 (cosimplicial object) 为 $\mathbb{\Delta }$ 到 $\mathsf{C}$ 的函子.

设 $X$ 是单纯集. 我们记$$X_n=X([n]),$$称此集合为 $X$ 的 $n$ 维单形的集合. $\mathbb{\Delta }$ 中态射 $d^i$ 和 $s^i$ 诱导了映射$$\begin{array}{rl}{d}_i:X_n\to X_{n-1}& (0\le i\le n),\\ s_i:X_n\to X_{n+1}& (0\le i\le n),\end{array}$$分别称为 $X$ 的面映射和退化映射.

例 3.5.

•	单纯集 $\Delta [n]$ 就是标准 $n$ 维单形 (作为单纯复形) 对应的单纯集, 也即由 $[n]$ 表出的预层. 它的 $k$ 维单形对应于保序映射 $[k]\to [n]$, 这里 $[n]=\{0,1,\dots ,n\}$ 视为其顶点的标号集. 由 Yoneda 引理, 对任何单纯集 $X$, 有$$X_n\simeq \mathsf{s}\mathsf{S}\mathsf{e}\mathsf{t}(\Delta [n],X).$$
•	这样, $\Delta [-]$ 就是 $\mathsf{s}\mathsf{S}\mathsf{e}\mathsf{t}$ 中的余单纯对象, 即一个余单纯单纯集.
•	在 $\Delta [n]$ 中去掉其内部, 就得到了其边界 $\partial \Delta [n]$. 其 $k$ 维单形对应于不满的保序映射 $[k]\to [n]$.
•	单纯集 $S^n$ 定义为商单纯集 $\Delta [n]/\partial \Delta [n]$, 这里的商可以逐个维数来定义.

命题 3.6. 范畴 $\mathsf{s}\mathsf{S}\mathsf{e}\mathsf{t}$ 是完备、余完备的, 即具有所有小的极限、余极限. 这些极限、余极限可以逐个维数给出, 例如$$(X\times Y{)}_n=X_n\times Y_n.$$

证明. 留给读者.

$\square$

例如, $\Delta [1]\times \Delta [1]$ 是一个实心正方形:它有 $2$ 个非退化 $2$ 维单形, 有 $5$ 个非退化 $1$ 维单形, 总共有 $9=3\times 3=5+4$ 个 $1$ 维单形 (包括退化单形在内).

几何实现

单纯集常常被视作带有顶点排序的单纯复形. 如果忘掉顶点排序, 我们就得到一个单纯复形, 这称为单纯集的几何实现. 下面, 我们来严格地说明这一过程.

命题 3.7. 每个单纯集都能通过从 $\varnothing$ 开始, 每次沿着 $\partial \Delta [n]$ 粘上一个 $\Delta [n]$, 然后取余极限而得到.

$\square$

在范畴 $\mathsf{T}\mathsf{o}\mathsf{p}$ 中, 我们有标准 $n$ 维单形, 记作 ${\Delta }^n$. 所有这些空间构成 $\mathsf{T}\mathsf{o}\mathsf{p}$ 中一个余单纯对象 (定义 3.4) ${\Delta }^{\bullet }$. 它指定了 “$\Delta [n]$ 在 $\mathsf{T}\mathsf{o}\mathsf{p}$ 中应该长什么样子”. 通过对象 ${\Delta }^{\bullet }$, 可以定义一个函子$$|-|:\mathsf{s}\mathsf{S}\mathsf{e}\mathsf{t}\to \mathsf{T}\mathsf{o}\mathsf{p},$$它将 $\Delta [n]$ 映到 ${\Delta }^n$, 然后通过取余极限, 将这个函子定义在所有单纯集上. 这个函子就称为几何实现 (geometric realization).

并且, 函子 $|-|$ 有右伴随 $\mathrm{Sing}:\mathsf{T}\mathsf{o}\mathsf{p}\to \mathsf{s}\mathsf{S}\mathsf{e}\mathsf{t}$, 定义为$$(\mathrm{Sing}X{)}_n=\mathsf{T}\mathsf{o}\mathsf{p}({\Delta }^n,X),$$这和上文中的定义一样.

事实上, 上述情况是以下构造的特例.

构造 3.8. 设 $\mathsf{C}$ 是余完备范畴. 如果给定 $\mathsf{C}$ 中的一个余单纯对象 ${\Delta }^{\bullet }$, 我们就能知道 “$\Delta [n]$ 在 $\mathsf{C}$ 中应该长什么样子”, 从而, 与上述构造同理, 能得到一对伴随函子

在下文中, 很多有关单纯集的构造都将通过这种方式给出. 我们举一个例子.

例 3.9. 取 $\mathsf{C}=\mathsf{C}\mathsf{h}(R)$ 为 $R$-模的上链复形的范畴, 其中 $R$ 是交换环. 我们取$${\Delta }^n=(\cdots \to 0\to \underset{\begin{array}{c}\\ (-n)\end{array}}{R^{\oplus \left(\genfrac{}{}{0ex}{}{n+1}{n+1}\right)}}\to \cdots \to \underset{\begin{array}{c}\\ (-1)\end{array}}{R^{\oplus \left(\genfrac{}{}{0ex}{}{n+1}{2}\right)}}\to \underset{\begin{array}{c}\\ (0)\end{array}}{R^{\oplus (n+1)}}\to 0\to \cdots )$$为标准 $n$-单形的单纯链复形 (即用来定义单纯同调的链复形). 这样, 构造 3.8 给出了函子 $\mathsf{s}\mathsf{S}\mathsf{e}\mathsf{t}\to \mathsf{C}\mathsf{h}(R)$, 它计算单纯集的单纯同调. 复合函子$$\mathsf{T}\mathsf{o}\mathsf{p}\stackrel{\mathrm{Sing}}{\to }\mathsf{s}\mathsf{S}\mathsf{e}\mathsf{t}\to \mathsf{C}\mathsf{h}(R)$$计算拓扑空间的奇异同调.

我们回到伴随函子 $|-|⊣\mathrm{Sing}$. 下面, 我们说明, 这一对函子实际上是 Quillen 等价, 从而 $\mathsf{s}\mathsf{S}\mathsf{e}\mathsf{t}$ 与 $\mathsf{T}\mathsf{o}\mathsf{p}$ 带有等价的同伦理论.

定义 3.10. 设 $0\le i\le n$. 单纯集 ${\Lambda }_i[n]$ 定义为在 $\partial \Delta [n]$ 中去掉第 $i$ 个顶点所对的面, 而得到的单纯集, 称为 $\Delta [n]$ 的第 $i$ 个尖角 (horn).

定理 3.11. 范畴 $\mathsf{s}\mathsf{S}\mathsf{e}\mathsf{t}$ 具有标准模型结构, 描述如下:

•	$\mathsf{W}=\{\text{拓扑空间的弱同伦等价}\}$.
•	$\mathsf{C}\mathsf{o}\mathsf{f}=\{\text{单射}\}$.
•	$\mathsf{F}\mathsf{i}\mathsf{b}=\mathrm{RLP}\{{\Lambda }_i[n]\hookrightarrow \Delta [n]\mid 0\le i\le n,n>0\}$.
•	$\mathsf{F}\mathsf{i}\mathsf{b}\cap \mathsf{W}=\mathrm{RLP}\{\partial \Delta [n]\hookrightarrow \Delta [n]\mid n\ge 0\}$.

定理的证明十分繁琐, 见 [Hovey, Theorem 3.6.5].

定理 3.12. 伴随函子 $|-|⊣\mathrm{Sing}$ 是 $\mathsf{s}\mathsf{S}\mathsf{e}\mathsf{t}$ (带有标准模型结构) 与 $\mathsf{T}\mathsf{o}\mathsf{p}$ (带有 Quillen 模型结构) 之间的 Quillen 等价.

见 [Hovey, Theorem 3.6.7]. 实际上, 证明它们是 Quillen 伴随并不难, 读者可以自己完成.

用单纯集描述范畴

单纯集可以看成范畴的一种模型. 例如, 单纯集 $\Delta [2]$ 可以看成下面的图表:其中双箭头的含义是, 该 $2$ 维单形 “验证” 了上方两个箭头的复合是下方的箭头. 在普通的范畴中, 该图表也就是 $2$ 个箭头接在一起:$$\bullet ⟶\bullet ⟶\bullet .$$有的人将这个图表记作 $2$, 因为它是偏序集 $[2]=\{0,1,2\}$ 对应的范畴.

又例如, 单纯集 $\Delta [2]\times \Delta [1]$ 对应于图表

这一想法的严格含义如下.

定义 3.13. 设 $\mathsf{C}$ 是小范畴. $\mathsf{C}$ 的脉 (nerve) 是单纯集 $N(\mathsf{C})$, 其 $n$ 维单形对应于 $\mathsf{C}$ 中 $n$ 个箭头构成的序列$$\bullet ⟶\bullet ⟶\cdots ⟶\bullet .$$其第 $0$ 个、第 $n$ 个面映射分别定义为去掉第一个、最后一个箭头; 对 $0<i<n$, 其第 $i$ 个面映射定义为将第 $i$ 个、第 $i+1$ 个箭头复合起来. 其退化映射定义为在序列中插入恒同箭头.

读者可以验证, 在以上几个例子中, 单纯集确实是相应范畴的脉.

注 3.14. 事实上, 脉是构造 3.8 的又一个特例. 我们在 $\mathsf{C}\mathsf{a}\mathsf{t}$ 中考虑余单纯对象 ${\Delta }^{\bullet }$, 定义为$${\Delta }^n=\bullet ⟶\bullet ⟶\cdots ⟶\bullet ,$$其中有 $n$ 个连续的箭头. 这个余单纯对象告诉我们 “$\Delta [n]$ 在 $\mathsf{C}\mathsf{a}\mathsf{t}$ 中应该长什么样子”. 这样, 我们得到一对伴随函子其中右伴随就是上面定义的脉函子.

注 3.15. 并非所有单纯集都能看成范畴, 例如在 ${\Lambda }_1[2]$ 中, 有两个箭头, 它们不能复合.

事实上, 如果我们定义 $\mathrm{Sp}(n)\subset \Delta [n]$ 为所有顶点和所有棱 $[i,i+1]$ $(0\le i<n)$ 构成的单纯子集, 称为脊 (spine), 那么对任何单纯集 $X$, 它是某个范畴的脉, 当且仅当对任何 $n\ge 0$, 它都满足提升性质

Kan 复形与拟范畴

Kan 复形是 “看起来像拓扑空间” 的单纯集, 我们将用它来描述 $\infty$-群胚.

定义 3.16. Kan 复形 (Kan complex) 是纤维性的单纯集. 换言之, 它满足尖角填充性质, 即提升性质其中 $0\le i\le n,n>0$.

例 3.17. 单纯集 $\Delta [n]$ 在 $n\ge 1$ 时不是 Kan 复形, 因为尖角$$\begin{array}{rl}{\Lambda }_0[2]& \to \Delta [n],\\ 0,1,2& \mapsto 0,1,0\end{array}$$无法填充为一个 $\Delta [2]$. 出现这一现象的原因是, $\Delta [n]$ 作为范畴, 并不是所有态射都可逆. 通过此例也可看出, Kan 复形具有类似群胚的性质.

例 3.18. 对任何拓扑空间 $X$, 其奇异单纯集 $\mathrm{Sing}X$ 是 Kan 复形, 这一点不难证明. 因此, 对任何单纯集 $S$, 单纯集 $\mathrm{Sing}|S|$ 可以用作 $S$ 的一个纤维性替换.

如上所言, Kan 复形看起来像是带有高阶结构的群胚. 在 Kan 复形中, $1$-态射都可逆, 但只是在相差一个 $2$-态射 (即 $2$ 维单形) 的意义下可逆. 对于高阶的态射来说, 尖角填充性质保证了高阶的态射也都可逆, 但是在相差一个更高阶态射的意义下可逆. 这段话描述的正是 $\infty$-群胚的概念.

定义 3.19. $\infty$-群胚, 或者说 $(\infty ,0)$-范畴, 就定义为 Kan 复形.

例如, 对拓扑空间 $X$ 而言, Kan 复形 $\mathrm{Sing}X$ 就是 $X$ 的基本 $\infty$-群胚.

定义 3.20. 同伦型 (homotopy type) 是指 $\infty$-群胚的同伦等价类, 即 $\mathrm{Ho}(\mathsf{s}\mathsf{S}\mathsf{e}\mathsf{t})$ 中的一个同构类. 这一范畴也等价于 $\mathrm{Ho}(\mathsf{T}\mathsf{o}\mathsf{p})\simeq \mathsf{h}\mathsf{C}\mathsf{W}$, 从而同伦型也是 CW 复形的同伦等价类.

下面, 我们通过类似的方式来定义 $(\infty ,1)$-范畴. 下表列出了尖角填充对应的范畴性质, 这里我们考虑范畴的脉.

尖角	性质
${\Lambda }_0[2]$	每个态射都有左逆
${\Lambda }_1[2]$	态射可复合
${\Lambda }_2[2]$	每个态射都有右逆
${\Lambda }_0[3]$	每个态射都是满态射
${\Lambda }_1[3]$, ${\Lambda }_2[3]$	态射复合的结合律
${\Lambda }_3[3]$	每个态射都是单态射
其它	(任何范畴都满足)

作为练习, 读者可以验证表中提到的性质.

我们注意到, ${\Lambda }_0[2]$、${\Lambda }_2[2]$、${\Lambda }_0[3]$、${\Lambda }_3[3]$ 这几个尖角的填充性质并非所有范畴都满足, 但对 “内尖角” 而言, 即 ${\Lambda }_i[n]$ $(0<i<n)$, 其填充性质描述了范畴应该满足的性质.

定义 3.21. 拟范畴 (quasi-category), 或者说 $(\infty ,1)$-范畴, 是指一个单纯集, 对 $0<i<n$ 满足提升性质换言之, 内尖角都可填充.

这里的术语需要多说明一下. 拟范畴是 $(\infty ,1)$-范畴的若干种模型之一, Kan 复形是 $\infty$-群胚的若干种模型之一. 因此, 在建立无穷范畴理论的基础时, 我们总说 “拟范畴” 和 “Kan 复形”, 以保证准确性.

地图

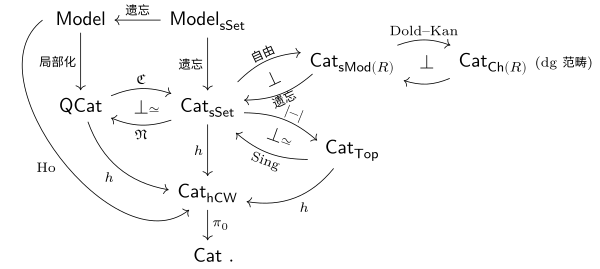
在研究 $(\infty ,1)$-范畴时, 我们将使用很多模型和工具. 现在, 我们已经完成了大部分的定义, 可以将之后的计划画成一张地图, 以便读者预览之后的内容, 也便于理清各概念的关系.

我们引入一些记号. 对幺半范畴 $\mathsf{V}$, 记 ${\mathsf{C}\mathsf{a}\mathsf{t}}_{\mathsf{V}}$ 为充实于 $\mathsf{V}$ 的范畴构成的范畴. (我们暂时忽略集合论问题, 下同.) 记 $\mathsf{M}\mathsf{o}\mathsf{d}\mathsf{e}\mathsf{l}$ 为模型范畴的范畴. 记 ${\mathsf{M}\mathsf{o}\mathsf{d}\mathsf{e}\mathsf{l}}_{\mathsf{V}}$ 为充实于 $\mathsf{V}$ 的模型范畴 (还未定义) 构成的范畴. 记 $\mathsf{Q}\mathsf{C}\mathsf{a}\mathsf{t}$ 为拟范畴的范畴 (它在下图中其实该写成 $\mathsf{s}\mathsf{S}\mathsf{e}\mathsf{t}$, 原因将在之后解释).

这个图表在某种意义下是 “交换” 的, 我们将在之后说明其细节. 所有位于 ${\mathsf{C}\mathsf{a}\mathsf{t}}_{\mathsf{h}\mathsf{C}\mathsf{W}}$ 之上的结构都能看作 $(\infty ,1)$-范畴的模型. 这些范畴中的同伦理论称为同伦相容 (homotopy coherent) 的, 而 ${\mathsf{C}\mathsf{a}\mathsf{t}}_{\mathsf{h}\mathsf{C}\mathsf{W}}$ 中的交换图仅仅只是同伦交换 (homotopy commutative) 的. 这两者的区别在于, 例如, 有的同伦交换的图表并不来自于一个真正交换的图表, 这样的图表就不是同伦相容的.

在图中还能看到, 同调代数, 也就是 dg (微分分次) 范畴的研究, 也与 $(\infty ,1)$-范畴的理论密切相关. 我们将利用这一关系, 将 $(\infty ,1)$-范畴的理论应用到同调代数上.