2. 模型范畴
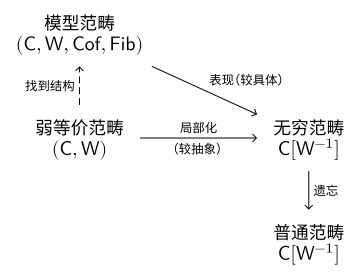
模型范畴 (model category) 是带额外结构的弱等价范畴, 这里的额外结构包括一类态射 , 称为余纤维化 (cofibration), 及一类态射 , 称为纤维化 (fibration). 这些信息将帮助我们在无穷范畴中进行具体计算. 我们回忆上一节中的图式:
模型范畴的实用性主要体现于以下两点.
• | 映射间的同伦可以被具体描述: 在局部化之后, 我们知道弱等价变成了可逆态射 (即同伦等价), 但我们并不知道哪些态射变得同伦. 但在模型范畴中, 我们能清晰地看到映射间的同伦, 也能看到同伦之间的高阶同伦, 就像在拓扑空间范畴中一样. 这样, 局部化 可以描述为模型范畴 的同伦范畴. |
• | 导出函子易于计算. 例如, 同伦极限、同伦余极限是一类重要的导出函子, 模型范畴理论提供了计算它们的方法. |
本节将介绍模型范畴的定义, 并阐明上述两点的对应理论.
定义与例子
我们回忆, 在代数拓扑中, 拓扑空间的映射 称为 Hurewicz 纤维化, 如果对任何空间 及任意实线图表存在虚线箭头使图表交换. 映射 称为 Hurewicz 余纤维化, 如果对任何空间 及任意实线图表存在虚线箭头使图表交换. 这里 是所有映射 构成的空间, 带有紧开拓扑.
定义 2.1. 设 是范畴, 是一类态射.
• | 称 中态射 对 具有右提升性质 (right lifting property), 如果对 中任意实线图表其中态射 在 中, 存在虚线箭头使图表交换. 所有具有此性质的态射 构成的类记为 . |
• | 称 中态射 对 具有左提升性质 (left lifting property), 如果对 中任意实线图表其中态射 在 中, 存在虚线箭头使图表交换. 所有具有此性质的态射 构成的类记为 . |
例如, 由定义,
作为练习, 读者可以证明 , 从而若记 , 以及 , 则 且 .
定义 2.2. 弱分解系统 (weak factorization system) 是三元组 , 其中 是范畴, 是两类态射, 使得
• | 且 . |
• | 中每个态射 都能分解为其中 且 . 并且, 我们要求这样的分解关于 具有函子性. |
例如, 记 、、 分别为闭 Hurewicz 余纤维化、Hurewicz 纤维化、同伦等价构成的类. 我们将看到, 三元组 和 都是弱分解系统.
命题 2.3. 设 是弱分解系统.
• | 和 均包含 中所有同构. |
• | 和 均关于态射复合封闭. |
• | 关于推出封闭, 关于拉回封闭. |
定义 2.4. 模型范畴 (model category) 是四元组 , 其中 是范畴, 是三类态射, 满足以下条件:
• | 完备、余完备, 也就是具有所有小极限、小余极限. |
• | 是弱等价范畴. |
• | 是弱分解系统. |
• | 是弱分解系统. |
我们引入以下术语:
• | 中态射称为弱等价 (weak equivalence). |
• | 中态射称为余纤维化 (cofibration). |
• | 中态射称为纤维化 (fibration). |
• | 中态射称为平凡余纤维化 (trivial cofibration). |
• | 中态射称为平凡纤维化 (trivial fibration). |
• | 称对象 是余纤维性 (cofibrant) 的, 如果 是余纤维化, 其中 是 的始对象. (始对象存在, 因为 余完备.) |
• | 称对象 是纤维性 (fibrant) 的, 如果 是纤维化, 其中 是 的终对象. (终对象存在, 因为 完备.) |
注意 和 两者中, 任一个都能确定另一个, 因为弱分解系统的两类态射能互相确定.
另外, 注意到余纤维化、平凡余纤维化都关于推出封闭, 而纤维化、平凡纤维化都关于拉回封闭.
我们来看一些例子. 我们将直接给出结果, 而略过证明, 因为每个例子的证明都十分繁琐. 细节可参见 [Hovey].
例 2.5. 上的 Hurewicz 模型结构由以下性质确定:
• | 是同伦等价构成的类. |
• | 是闭 Hurewicz 余纤维化构成的类. |
• | 是 Hurewicz 纤维化构成的类. |
例 2.6. 上的 Quillen 模型结构由以下性质确定:
• | 是弱同伦等价构成的类. |
• | , 也就是 Serre 纤维化构成的类. |
• | . |
• | . 特别地, 映射 是余纤维化. |
在这个模型范畴中, 所有拓扑空间都是纤维性的; 所有 CW 复形都是余纤维性的, 因为余纤维化被推出、复合、序列余极限保持.
下文中, 我们总是使用 Quillen 模型结构, 而不用 Hurewicz 模型结构.
例 2.7. 上的投射模型结构由以下性质确定:
• | 是拟同构构成的类. |
• | 是 (逐个位置) 满射构成的类. |
在这个模型范畴中, 所有上链复形都是纤维性的; 所有由投射模构成的上有界上链复形, 例如 -模的投射消解, 都是余纤维性的.
例 2.8. 上的内射模型结构由以下性质确定:
• | 是拟同构构成的类. |
• | 是 (逐个位置) 单射构成的类. |
在这个模型范畴中, 所有上链复形都是余纤维性的; 所有由内射模构成的下有界上链复形, 例如 -模的内射消解, 都是纤维性的.
在模型范畴中, 一类特殊的对象是双纤维性对象 (cofibrant-fibrant object), 也就是既余纤维性、又纤维性的对象. 它们具有类似 CW 复形或投射、内射消解的性质. 我们将看到, 这类对象具有十分良好的性质. 并且, 每个对象都弱等价于一个双纤维性对象.
构造 2.9. 设 是模型范畴, 设 . 由模型范畴的公理, 态射 可以分解为则 具有余纤维性, 且弱等价于 . 并且, 是一个函子, 称为余纤维性替换 (cofibrant replacement).
类似地, 态射 可以分解为则 具有纤维性, 且弱等价于 . 并且, 是一个函子, 称为纤维性替换 (fibrant replacement).
一般地, 任何具有上述性质的函子 (或 ) 都可以被称为余纤维性替换 (或纤维性替换).
命题 2.10. 沿用上述记号, 则 与 都具有双纤维性, 且弱等价于 .
同伦
下面, 我们来说明如何从模型范畴的公理出发, 恢复出映射间 “同伦” 的概念.
在拓扑中, 两个映射 之间的同伦由一个映射给出. 在模型范畴中, 我们通过模仿 和 的构造, 来定义同伦.
定义 2.11. 设 是模型范畴, 是一个对象.
• | 的柱对象 (cylinder object), 记作 , 是指余对角映射 的一个分解: 如果还满足 , 就称此柱对象称为好 (very good) 的. |
• | 的路径对象 (path space object), 记作 , 是指对角映射 的一个分解: 如果还满足 , 就称此路径对象称为好 (very good) 的. |
这也就是拓扑中 和 的类比. 模型范畴的公理表明, 好柱对象、好路径对象都一定存在.
定义 2.12. 设 是 中两个态射.
• | 从 到 的左同伦 (left homotopy) 是一个态射 , 使得图表交换. 此时, 称 左同伦于 . |
• | 从 到 的右同伦 (right homotopy) 是一个态射 , 使得图表交换. 此时, 称 右同伦于 . |
在拓扑中, 左同伦与右同伦是等价的. 我们将看到, 这一点对双纤维性对象成立. 不过在此之前, 我们先通过一个具体例子, 来熟悉公理化同伦论的运作方式.
例 2.13. 设 是左同伦的态射, 也是左同伦的态射. 则 与 也左同伦. 这里, 我们假设左同伦使用的柱对象都是典范的柱对象, 也就是通过模型范畴的公理分解 和 的余对角映射, 而得到的柱对象.
证明. 在拓扑中, 这件显然的事是通过考虑映射来证明的, 其中第一个映射由任意一条连接 和 的道路 所诱导.
命题 2.14. 设 是两个态射. 如果 余纤维性, 且 纤维性, 则 与 左同伦当且仅当它们右同伦. 并且, 在此情况下, 对 的任意柱对象都存在左同伦, 对 的任意路径对象都存在右同伦.
证明. 设 是 与 间的左同伦. 证明的想法是构造一个 “从 到 的映射” , 如下图所示.
我们想要将右同伦 沿着端点处的左同伦 和 进行转移. 这个想法具体写下来, 就是在图表中进行提升. 读者可以利用 余纤维性这一条件, 验证图表中提到的细节. 这样, 复合态射给出了我们想要的右同伦.
上述命题表明, 对双纤维性对象而言, 同伦具有非常好的性质. 作为练习, 读者可以证明, 在命题的条件下, 态射的同伦是等价关系. 因此, 我们可以定义态射的同伦类, 从而定义同伦范畴.
定义 2.15. 的同伦范畴 (homotopy category) 是如下定义的范畴:
• | 对象: 的双纤维性对象. |
• | 态射: 中态射的同伦类. |
不要忘记, 我们研究模型范畴的最终目的是研究局部化. 因此, 下面的结论揭示了上述定义的意义:
定理 2.16. 有范畴等价
定理的证明需要用到以下结论:
命题 2.17 (Whitehead 定理). 设 为双纤维性对象, 为态射. 则 是弱等价当且仅当它是同伦等价 (即具有同伦逆).
证明. 1. 如果 , 则 有右逆, 因为可以在图表中进行提升. 我们想证明 是 的同伦逆, 也就是证明 同伦于 . 只需在图表中提升即可.
2. 如果 , 则上述论证的对偶版本就能证明命题.
注 2.18. 我们曾提到, 只是局部化提供的第一层信息, 而完整的信息需要由一个 -范畴来描述. 事实上, 模型范畴中也能看到这些高阶的信息, 但需要通过一种称为架 (framing) 的构造. 这种构造用来模拟拓扑中的 和 , 从而在模型范畴中描述高阶的同伦. 细节可参见 [Hovey, Chapter 5].
导出函子
在同调代数中, 导出函子是一种将 Abel 范畴间的函子 变成导出范畴间的函子 的方法. 这实际上是下面构造的特例.
设 是模型范畴, 分别记 中由余纤维性对象、纤维性对象、双纤维性对象构成的满子范畴为 、、.
定义 2.19. 设有函子 , 其中 是模型范畴, 是弱等价范畴.
• | 若 保持弱等价, 则 诱导了函子称为 的全导出函子 (total derived functor). |
• | 若 保持弱等价, 则有 (相差自然同构意义下的) 交换图其中 是 的任一余纤维性替换函子. 函子 称为 的左导出函子 (left derived functor). 从而, 对任何 , 在 中有 |
• | 若 保持弱等价, 则有 (相差自然同构意义下的) 交换图其中 是 的任一纤维性替换函子. 函子 称为 的右导出函子 (right derived functor). 从而, 对任何 , 在 中有 |
例 2.20. 考虑上链复形范畴 上的投射模型结构 (例 2.7). 此时, 余纤维性替换就是取投射消解. 因此, 左导出函子与同调代数中的定义相同.
类似地, 考虑上链复形范畴 上的内射模型结构 (例 2.8). 此时, 纤维性替换就是取内射消解, 这与同调代数中定义右导出函子的方法相同.
导出伴随函子
在这一节, 我们描述一种情况, 即一对伴随函子在满足某个条件时, 两个函子都有导出函子, 并且其导出函子仍为一对伴随.
定义 2.21. 设 为模型范畴. 一对伴随函子称为 Quillen 伴随 (Quillen adjunction), 如果 保持余纤维化和平凡余纤维化.
注意, 由于提升性质, 保持余纤维化当且仅当 保持平凡纤维化, 保持平凡余纤维化当且仅当 保持纤维化.
引理 2.22 (Ken Brown). 设 是模型范畴间的函子. 如果 保持平凡余纤维化, 那么 保持弱等价.
推论 2.23. 设 是模型范畴 、 间的 Quillen 伴随. 则导出函子 、 都存在, 并且构成一对伴随
定义 2.24. 一对 Quillen 伴随 称为 Quillen 等价 (Quillen equivalence), 如果 和 是范畴等价.
Quillen 等价不一定是范畴等价, 但我们将看到, 经过局部化, Quillen 等价诱导相应的 -范畴间的范畴等价. 这是证明无穷范畴之间范畴等价的一种好用的方法.
命题 2.25. 设 是模型范畴 、 间的 Quillen 等价, 设 是余纤维性对象, 是纤维性对象. 则余单位映射和单位映射都是弱等价.