1.4. 全纯域及其性质

全纯域

因为多复变函数中 Hartogs 现象 (有些区域上的任意全纯函数都可以延拓到更大范围) 的出现, 可以自然地提问:

•	给定一个区域 $\Omega \subset {\mathbb{C}}^n$, 是否能找到一个 “最大的区域” $E(\Omega )\subset \Omega$, 使得下式成立?$$\mathcal{O}(\Omega )=\mathcal{O}(E(\Omega )){|}_{\Omega }.$$

•	如果上述 $E(\Omega )$ 存在, 它是否在全纯等价的意义下是唯一的? 它有什么性质, 如何刻画它?

事实上, $E(\Omega )$ 确实是存在的, 而且在全纯等价含义下是唯一的, 如果 $\mathcal{O}(E(\Omega ))$ 分离 $E(\Omega )$ 中的点. 然而, 这种唯一的 $E(\Omega )$ 并非 ${\mathbb{C}}^n$ 的区域, 它只是一个 $n$ 维 Stein 流形, 拥有一个映到 ${\mathbb{C}}^n$ 的局部双全纯映射. (参考 Hörmander 书第五章的 5.4 节以获取细节)

如今我们把情况限制在 $E(\Omega )$ 在 ${\mathbb{C}}^n$ 中, 且只考虑在特定的某种凸性下刻画 $E(\Omega )$ 的问题. 注意到 $E(\Omega )$ 是通过经典的解析延拓构造的, 如下的概念是自然的.

定义 1.4.1 (全纯域). 区域 $\Omega \subset {\mathbb{C}}^n$ 被称为是全纯域, 如果对于任意与 $\partial \Omega$ 有交的区域 $U\subset {\mathbb{C}}^n$, 以及 $U\cap \Omega$ 的任意连通分支 $V$, 存在 $f\in \mathcal{O}(\Omega )$ 使得 $f{|}_V$ 不存在 $U$ 上的全纯延拓.

定义 1.4.2. 设 $\Omega ⊊{\mathbb{C}}^n$ 是区域, $p\in \partial \Omega$. 函数 $f\in \mathcal{O}(\Omega )$ 被叫做是在 $p$ 点处完全奇异, 如果对于任意 $p$ 的邻域 $U\subset {\mathbb{C}}^n$, 和任意 $U\cap \Omega$ 的连通分支 $V$, $f{|}_V$ 不存在 $U$ 上的全纯延拓.

下面先举两个例子.

•	令 $\Omega =\mathbb{C}\backslash (-\infty ,0]$, $f$ 为 $\Omega$ 上的对数函数. 则 $f$ 在 $0$ 处完全奇异, 但在任意 $x\in (-\infty ,0)$ 处均非完全奇异.

•	令 $\Omega =\Delta \subset \mathbb{C}$ 为单位圆盘, 下面三个函数均在 $\partial \Delta$ 的任一点都完全奇异:

$$f(z)=\sum _{k=0}^{\infty }{z}^{k!},g(z)=\sum _{k=1}^{\infty }\frac{z^{k!}}{k^2},h(z)=\sum _{k=0}^{\infty }\frac{z^{2^k}}{2^k}.$$

为了说明一个区域 $\Omega ⊊{\mathbb{C}}^n$ 是全纯域, 只需要说明对任意 $p\in \partial \Omega$, 都能找到一个函数 $f\in \mathcal{O}(\Omega )$, 它是在 $p$ 处完全奇异的. 下一节会说明反过来也正确, 而且有更多的结论. 现在先通过上述结论判定部分全纯域.

•	任何区域 $\Omega \subset \mathbb{C}$ 都是全纯域. 如果 $\Omega =\mathbb{C}$, 结论是显然的; 否则, 对任意 $p\in \partial \Omega$, 函数 $f_p(z)=(z-p{)}^{-1}\in \mathcal{O}(\Omega )$ 在 $p$ 处是完全奇异的.

•	任何凸区域 $\Omega \subset {\mathbb{C}}^n$ 都是全纯域. 考虑 $\Omega \ne {\mathbb{C}}^n$ 的情形, 取 $p\in \partial \Omega$. 因为 $\Omega$ 是凸集, 可以取它在点 $p$ 的支撑超平面$$H=\{z\in {\mathbb{C}}^n\mid \mathrm{Re}⟨z-p,v⟩=0\},$$并令 $f_p(z)=⟨z-p,v{⟩}^{-1}$, 则 $f_p$ 在点 $p$ 完全奇异.

定义 1.4.3. 设 $\Omega \subset {\mathbb{C}}^n$ 是区域, $K\subset \subset \Omega$. 定义$${\hat{K}}_{\Omega }={\hat{K}}_{\mathcal{O}(\Omega )}=\{z\in \Omega \mid |f(z)|\le \underset{K}{\sup }|f|,\forall f\in \mathcal{O}(\Omega )\},$$称为 $K$ 在 $\Omega$ 中的全纯凸包.

注 1.4.4.

1.

${\hat{K}}_{\Omega }$ 包含于 $K$ 在 ${\mathbb{C}}^n$ 中的仿射凸包. (仿射凸包是集合中所有点的仿射组合组成的集合) 这是因为, 取 $f_v(z)=\exp ⟨z,v⟩,|v|=1$, 则有$${\hat{K}}_{\Omega }\subset \bigcap _{|v|=1}\{z\in {\mathbb{C}}^n\mid \mathrm{Re}⟨z,v⟩\le \underset{w\in K}{\sup }\mathrm{Re}⟨w,v⟩\},$$根据凸集分离定理, 右边正好就是 $K$ 在 ${\mathbb{C}}^n$ 中的仿射凸包.

2.

首先根据定义, ${\hat{K}}_{\Omega }$ 是 $\Omega$ 中的闭子集. 然而, 是否有 ${\hat{K}}_{\Omega }\subset \subset \Omega$ 则是一个问题. ∘ 如果 $n=1$, 则 ${\hat{K}}_{\Omega }$ 总是紧集. 这只需要取 $f(z)=(z-\zeta {)}^{-1},\forall \zeta \in \partial \Omega$, 然后得到 $\mathrm{dist}({\hat{K}}_{\Omega },\partial \Omega )=\mathrm{dist}(K,\partial \Omega )$. ∘ 如果 $n>1$, 则 ${\hat{K}}_{\Omega }$ 不必是紧集. 举例: 取 $\Omega ={\mathbb{C}}^n\backslash \{0\}$, 这样 $\mathcal{O}(\Omega )=\mathcal{O}({\mathbb{C}}^n)$, 且$${\widehat{(\partial {\mathbb{B}}^n)}}_{\Omega }={\bar{\mathbb{B}}}^n\backslash \{0\}.$$

定义 1.4.5 (全纯凸性). 区域 $\Omega \subset {\mathbb{C}}^n$ 被称为是全纯凸的, 如果对任意 $K\subset \subset \Omega$, ${\hat{K}}_{\Omega }$ 都是紧集.

注 1.4.6. 如果考虑实的情况, 会发现: 区域 $\Omega \subset {\mathbb{R}}^n$ 是凸的当且仅当对任意 $K\subset \subset \Omega$, 它的凸包都是紧集. 于是可以把全纯凸视为实情况中凸的类似物. 另外, 可以发现: ${\mathbb{C}}^n$ 中的凸集一定是全纯凸的, 这是因为注 1.4.4 中第二条第一点: $\mathbb{C}$ 的任何区域都是全纯凸的.

命题 1.4.7. 区域 $\Omega \subset {\mathbb{C}}^n$ 是全纯凸的当且仅当它有一个全纯凸正规穷竭, 也就是说: 存在一列紧集 $\{K_j\}$ 使得: ${\widehat{(K_j)}}_{\Omega }=K_j\subset K_{j+1}^{\circ },\forall j\ge 1$, 且 ${\bigcup }_{j=1}^{\infty }{K}_j=\Omega$.

习题. 证明命题 1.4.7.

Cartan–Thullen 定理

准备工作

现在我们的任务是叙述并证明有名的 Cartan–Thullen 定理, 它表明全纯域和 ${\mathbb{C}}^n$ 中的全纯凸域实际上是同样的东西.

令 $\Omega ⊊{\mathbb{C}}^n$ 是区域, $r\in (0,+\infty {)}^n$. 对任意 $z\in \Omega$, 定义$$\begin{array}{rl}{d}_{\Omega }^r(z)& =\sup \{\lambda >0\mid P(z,\lambda r)\subset \Omega \}\\ & =\inf \left\{\max \left\{\frac{|z_1-w_1|}{r_1},\cdots ,\frac{|z_n-w_n|}{r_n}\right\}|w\in \partial \Omega \right\}\end{array}$$接下来可以叙述并证明一个结论, 它将是我们通向 Cartan–Thullen 定理的钥匙.

引理 1.4.8. 设 $\Omega ⊊{\mathbb{C}}^n$ 是域, $K\subset \subset \Omega$, 以及 $f\in \mathcal{O}(\Omega )$. 设$$|f|\le d_{\Omega }^r\mathrm{on}K$$(1.4.1)对某个 $r\in (0,+\infty {)}^n$ 成立, 则对任意 $z\in {\hat{K}}_{\Omega }$ 和 $g\in \mathcal{O}(\Omega )$, $g$ 在点 $z$ 的 Taylor 展开式$$S_g(w)=\sum _{\alpha \in {\mathbb{N}}^n}\frac{{\partial }^{\alpha }g(z)}{\alpha !}(w-z{)}^{\alpha }$$在 $P(z,|f(z)|r)$ 中收敛.

注 1.4.9. 这个引理有一点需要注意: 对某些 $z\in {\hat{K}}_{\Omega }\backslash K$, 多圆柱 $P(z,|f(z)|r)$ 可能并不包含在 $\Omega$ 中, 而它的 (多重) 半径 $|f(z)|r$ 也与 $g\in \mathcal{O}(\Omega )\backslash \{f\}$ 无关. 总而言之, 对满足 $|f(z)|>d_{\Omega }^r(z)$ 的 $z\in {\hat{K}}_{\Omega }\backslash K$, 引理 1.4.8 同时得出另一个全纯延拓: 从 $\mathcal{O}(\Omega ){|}_{P(z,d_{\Omega }^r(z)r)}$ 到 $\mathcal{O}(\Omega ){|}_{P(z,|f(z)|r)}$(不是从 $\mathcal{O}(\Omega )$ 到 $\mathcal{O}(\Omega \cup P(z,|f(z)|r))$).

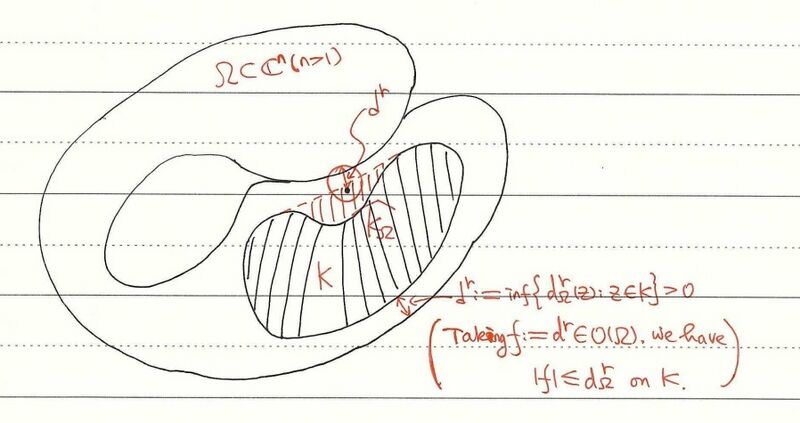
证明. 对任意 $t\in (0,1)$, 1.4.1 式表明: $$K_t:=\bigcup _{z\in K}\overline{P(z,t|f(z)|r)}\subset \subset \Omega .$$于是对任意 $g\in \mathcal{O}(\Omega )$, 有 $M_t:={\sup }_{K_t}|g|<\infty$. 类似 Cauchy 估计, 可得$$|f(z){|}^{|\alpha |}\cdot |{\partial }^{\alpha }g(z)|\le \frac{M_t\alpha !}{t^{|\alpha |}{r}^{\alpha }},\forall z\in K,\alpha \in {\mathbb{N}}^n.$$注意到 $f^{|\alpha |}{\partial }^{\alpha }g\in \mathcal{O}(\Omega )$, ${\hat{K}}_{\Omega }$ 的定义使得上面的不等式对任何 $z\in {\hat{K}}_{\Omega },\alpha \in {\mathbb{N}}^n$ 成立. 于是幂级数$$S_g(w)=\sum _{\alpha \in {\mathbb{N}}^n}\frac{{\partial }^{\alpha }g(z)}{\alpha !}(w-z{)}^{\alpha }$$在 $P(z,t|f(z)|r)$ 中收敛, $\forall t\in (0,1)$. 所以在 $P(z,|f(z)|r)$ 中也收敛.

$\square$

定义 1.4.10. 函数 $\delta :{\mathbb{C}}^n\to \mathbb{R}$ 被称为距离函数, 如果

1.	$\delta \in C({\mathbb{C}}^n)$ 且 $\delta >0\mathrm{on}{\mathbb{C}}^n\backslash \{0\}$;
2.	$\delta (\zeta z)=|\zeta |\delta (z),\forall \zeta \in \mathbb{C},z\in {\mathbb{C}}^n$.

设 $\Omega ⊊{\mathbb{C}}^n$ 是区域, $\delta$ 是距离函数. 令$${\delta }_{\Omega }(z)=\inf \{\delta (z-w)\mid w\in {\mathbb{C}}^n\backslash \Omega \},$$则不难证明

•	${\delta }_{\Omega }=0\mathrm{on}{\mathbb{C}}^n\backslash \Omega$;
•	${\delta }_{\Omega }{|}_{\Omega }=\inf \{\delta (\cdot -w)\mid w\in \partial \Omega \}>0$;
•	${\delta }_{\Omega }\in C({\mathbb{C}}^n)$.

定理 1.4.11. 设 $\Omega ⊊{\mathbb{C}}^n$ 是全纯域, $K\subset \subset \Omega$. 如果 $f\in \mathcal{O}(\Omega )$, 且$$|f|\le {\delta }_{\Omega }\mathrm{on}K,$$则$$|f|\le {\delta }_{\Omega }\mathrm{on}{\hat{K}}_{\Omega }.$$换言之, 有$$\underset{{\hat{K}}_{\Omega }}{\inf }{\delta }_{\Omega }=\underset{K}{\inf }{\delta }_{\Omega }.$$

证明. 第一步假设 $\delta$ 拥有如下的形式: $$\delta (z)=\max \left\{\frac{|z_1|}{r_1},\cdots ,\frac{|z_n|}{r_n}\right\},z\in {\mathbb{C}}^n,$$其中 $r\in (0,+\infty {)}^n$. 则 ${\delta }_{\Omega }=d_{\Omega }^r$. 根据引理 1.4.8, 对任意 $z\in {\hat{K}}_{\Omega }$ 和 $g\in \mathcal{O}(\Omega )$, $g$ 在点 $z$ 的 Taylor 展开式在 $P(z,|f(z)|r)$ 收敛. 注意到 $\Omega$ 是全纯域, 必有$$\bigcup _{z\in {\hat{K}}_{\Omega }}P(z,|f(z)|r)\subset \Omega ,$$从而 $|f|\le d_{\Omega }^r={\delta }_{\Omega }\mathrm{on}{\hat{K}}_{\Omega }$.

现在证明一般情况. 注意到$${\delta }_{\Omega }(z)=\inf \{{\delta }_v(z,\partial \Omega )\mid v\in {\mathbb{C}}^n\backslash \{0\}\},z\in \Omega ,$$其中$$\begin{array}{rl}{\delta }_v(z,\partial \Omega )& =\inf \{\delta (z-w)\mid w\in ({\mathbb{C}}^n\backslash \Omega )\cap (\{z\}+\mathbb{C}v\})\}\\ & =\sup \left\{\lambda >0|z+\zeta \frac{v}{\delta (v)}\in \Omega ,\forall \zeta \in \Delta (0,\lambda )\right\},\end{array}$$则只需证明$$|f|\le {\delta }_v(\cdot ,\partial \Omega ),\forall v\in {\mathbb{C}}^n\backslash \{0\}.$$(1.4.2)现在任取 $U\in \mathrm{U}(n)$($n$ 阶酉群), 则 $U\Omega$ 仍是全纯域, 且

•	${\widehat{(UK)}}_{U\Omega }=U{\hat{K}}_{\Omega }$;
•	${\delta }_{\Omega }\circ U^{-1}=(\delta \circ U^{-1}{)}_{U\Omega }$;
•	${\delta }_v(z,\partial \Omega )={\delta }_{Uv}(Uz,\partial (U\Omega ))$.

于是, 为了证明 1.4.2 式, 可不妨设 $v=(|v|,0,\cdots ,0)$. 对 $k\in {\mathbb{N}}^{\ast }$, 令 $v_k=(|v|,1/k,\cdots ,1/k)$, 则可以证明$$\delta (v)d_{\Omega }^{v_k}\nearrow {\delta }_v(\cdot ,\partial \Omega ),k\to \infty .$$因为 $|f|\le {\delta }_{\Omega }\mathrm{on}K$, 所以$$\max \left\{\frac{|f|}{\delta (v)d_{\Omega }^{v_k}},1\right\}\searrow 1\mathrm{on}K,k\to \infty .$$式子左边的函数都属于 $C(\Omega )$. 根据 (函数列收敛性的) Dini 定理, 对任意 $\epsilon >0$, 存在 $k\in {\mathbb{N}}^{\ast }$ 使得$$|f|\le (1+\epsilon )\delta (v)d_{\Omega }^{v_k}\mathrm{on}K.$$不等式右边是具有第一步所述形式的距离函数. 根据第一步证明的结果, 同样的不等式将在 ${\hat{K}}_{\Omega }$ 成立, 于是$$|f|\le (1+\epsilon )\delta (v)d_{\Omega }^{v_k}\le (1+\epsilon ){\delta }_v(\cdot ,\partial \Omega )\mathrm{on}{\hat{K}}_{\Omega }.$$令 $\epsilon \to 0$ 就得到 1.4.2 式.

$\square$

注 1.4.12. 1.4.1 式无法使用上述证明中类似的方法. 原因是: 序列$$\left\{\frac{|f|}{\delta (v)d_{\Omega }^{v_k}}\right\}$$的极限 $\frac{|f|}{{\delta }_v(\cdot ,\partial \Omega )}$ 并非总是连续函数, 而只是上半连续函数.

定理与证明

现在可以叙述并证明主要结论, 也就是 Cartan–Thullen 定理. 它给予全纯域一种利用全纯凸性的刻画.

定理 1.4.13 (Cartan–Thullen 定理). 设 $\Omega ⊊{\mathbb{C}}^n$ 是区域. 下面的八个断言等价:

1.	对任意 $p\in \partial \Omega$, 都存在 $f\in \mathcal{O}(\Omega )$ 在点 $p$ 完全奇异.
2.	$\Omega$ 是全纯域.
3.	对任意 $K\subset \subset \Omega$ 和 $f\in \mathcal{O}(\Omega )$, 我们有$$\underset{{\hat{K}}_{\Omega }}{\sup }\frac{|f|}{{\delta }_{\Omega }}=\underset{K}{\sup }\frac{|f|}{{\delta }_{\Omega }}$$对某个 (从而是所有的) 距离函数 $\delta$ 成立.
4.	对任意 $K\subset \subset \Omega$ , 我们有$$\underset{{\hat{K}}_{\Omega }}{\sup }{\delta }_{\Omega }=\underset{K}{\sup }{\delta }_{\Omega }$$对某个 (从而是所有的) 距离函数 $\delta$ 成立.
5.	$\Omega$ 是全纯凸的.
6.	对任意由互不相同的点组成的, 无 $\Omega$ 中极限点的序列 $\{z_j\}\subset \Omega$ 和任意序列 $\{w_j\}\subset \mathbb{C}$, 都存在 $f\in \mathcal{O}(\Omega )$ 使得$$f(z_j)=w_j,\forall j\in {\mathbb{N}}^{\ast }.$$
7.	存在 $f\in \mathcal{O}(\Omega )$ 满足性质: 对任意 $p\in \partial \Omega$ 和 $p$ 的任意连通邻域 $U\subset {\mathbb{C}}^n$, $f$ 均在 $U\cap \Omega$ 的每个连通分支中都无界.
8.	存在 $f\in \mathcal{O}(\Omega )$, 它在 $\partial \Omega$ 的每一点处都完全奇异.

证明. 在正式开始之前, 先注意到如下逻辑关系:

所以剩余工作是证明 $5\Rightarrow 6\Rightarrow 7\Rightarrow 8$.

•

$5\Rightarrow 6$: 根据命题 1.4.7, 可令 $\{K_j\}$ 为 $\Omega$ 的一个全纯凸正规穷竭, 满足$$\{z_j\}\subset \Omega \backslash K_1.$$对每个 $j\in {\mathbb{N}}^{\ast }$, 可以找到一个唯一的 $v_j\in {\mathbb{N}}^{\ast }$ 使得 $z_j\in K_{v_j+1}\backslash K_{v_j}$. 于是, 可以找到 $f_j\in \mathcal{O}(\Omega )$ 使得$$\underset{K_{v_j}}{\sup }|f_j|<1=f_j(z_j).$$令 $p_1=1$, 且 $p_j(j\ge 2)$ 是满足$$p_j(z_j)=1,p_j(z_k)=0,k=1,2,\cdots ,j-1$$c 的 ${\mathbb{C}}^n$ 上的多项式. 令$$f:=\sum _{j=1}^{\infty }{\lambda }_j{p}_j{f}_j^{m_j},$$其中 ${\lambda }_j\in \mathbb{C},m_j\in {\mathbb{N}}^{\ast }$ 是精心选择的参数, 满足: $${\lambda }_1=w_1,\underset{K_{v_1}}{\sup }|{\lambda }_1{p}_1{f}_1^{m_1}|<2^{-1},$$以及$${\lambda }_j=w_j-\sum _{k=1}^{j-1}{\lambda }_k{p}_k(z_j)f_k^{m_k}(z_j),\underset{K_{v_j}}{\sup }|{\lambda }_j{p}_j{f}_j^{m_j}|<2^{-j},\forall j\ge 2.$$注意到 $\{z_j\}$ 没有 $\Omega$ 中的极限点, 有 $v_j\to \infty ,j\to \infty$, 从而上述定义了 $f$ 的级数在 $\Omega$ 中局部一致收敛. 于是 $f\in \mathcal{O}(\Omega )$. 而且: $f(z_1)=w_1$, 以及$$f(z_j)=\sum _{k=1}^j{\lambda }_k{p}_k(z_j)f_k^{m_k}(z_j)={\lambda }_j+\sum _{k=1}^{j-1}{\lambda }_k{p}_k(z_j)f_k^{m_k}(z_j)=w_j,\forall j\ge 2.$$这就找到了要求的 $f$.

•

$6\Rightarrow 7$: 先找一个 $\Omega$ 的正规穷竭. 我们有下述断言: 存在一列递增正整数 $\{v_j\}$ 和 $\{p_j\}\subset \Omega$ 使得$$p_j\in K_{v_{j+1}}\backslash K_{v_j},\forall j\in {\mathbb{N}}^{\ast },$$且对任意 $p\in \partial \Omega$ 和它的邻域 $U$, $U\cap \Omega$ 的每个连通分支都包含序列 $\{p_j\}$ 的无限个点. 有了这条断言, 则只需要注意到 $\{p_j\}$ 是互不相同且没有 $\Omega$ 中极限点的序列, 然后取函数 $f\in \mathcal{O}(\Omega )$ 使得 $f(p_j)=j$ 即可. 下面证明这条断言. 考虑 $\Omega$ 中所有的有理点 (理解为 ${\mathbb{R}}^{2n}$ 中的有理点). 构造序列 $\{z_k\}$, 其中的每个项都是上述有理点, 且每个有理点都在序列中出现无穷多次. 令 $v_1=1,v_2=2$, 以及 $p_1\in K_2\backslash K_1$. 现在归纳构造, 设 $j\ge 2$, 且 $p_1,\cdots ,p_{j-1};v_1,\cdots ,v_j$ 已经被找到, 它们满足$$p_k\in K_{v_{k+1}}\backslash K_{v_k},k=1,\cdots ,j-1.$$令 $r_j=\mathrm{dist}(z_j,\partial \Omega )$, 则 $B_j=B(z_j,r_j)$ 不被任何 $\Omega$ 的紧子集包含. 于是, 可以取 $p_j\in B_j\backslash K_{v_j}$, 并取 $v_{j+1}$ 使得 $p_j\in K_{v_{j+1}}$. 这样就构造出了想要的序列. 现在说明我们找到的 $\{p_j\}$ 符合断言所描述的性质. 设 $p\in \partial \Omega$, $U$ 是其连通邻域, $V$ 是 $U\cap \Omega$ 的一个连通分支. 注意到 $\varnothing \ne \partial V\cap U\subset \partial \Omega$, 可以找到点 $q\in \partial V\cap U$. 现在找一个有理点 $z(q)\in V$, 它与 $q$ 足够接近, 且$$B(z(q),\mathrm{dist}(z(q),\partial \Omega ))\subset U\cap \Omega$$(从而包含于 $V$). 注意到 $z(q)$ 在 $\{z_j\}$ 中无穷多次出现, 以及 $p_j\in B_j\backslash K_{v_j}$, 所以 $V$ 包含无穷多个 $p_j$.

•

$7\Rightarrow 8$: 设 $f$ 是第七条所说的函数. 如果它不是在 $\partial \Omega$ 的每一点完全奇异的, 设 $p_0\in \partial \Omega$ 是一个反例, 则有 $p_0$ 的连通邻域 $U_0$ 和 $U_0\cap \Omega$ 的一个连通分支 $V_0$, 使得存在 $\tilde{f}\in \mathcal{O}(U_0)$, 满足$$\tilde{f}{|}_{V_0}=f{|}_{V_0}.$$注意到 $\varnothing \ne \partial V_0\cap U_0\subset \partial \Omega$, 可以找到点 $q\in \partial V_0\cap U_0\subset \partial \Omega$, 以及其连通邻域 $U$, 使得 $U\subset \subset U_0$. 则 $V_0\cap (U\cap \Omega )=V_0\cap U\ne \varnothing$. 进一步, 可以找一个 $U\cap \Omega$ 的连通分支 $V$ 使得 $V\cap V_0\ne \varnothing$. 这导致 $V\subset V_0$, 从而$$\underset{V}{\sup }|f|=\underset{V}{\sup }|\tilde{f}|\le \underset{\bar{U}}{\sup }|\tilde{f}|<\infty ,$$与第七条所述无界性矛盾.

至此证明了定理的所有部分.

$\square$

Cartan–Thullen 定理的推论

我们可以按次序给出定理 1.4.13 的如下推论.

推论 1.4.14. 令 $\{{\Omega }_{\alpha }{\}}_{\alpha \in \mathcal{A}}$ 为一族 ${\mathbb{C}}^n$ 中的全纯域. 则交集 ${\bigcap }_{\alpha \in \mathcal{A}}{\Omega }_{\alpha }$ 的内部的任何连通分支也都是全纯域.

证明. 不妨设 $\varnothing \ne {\left({\bigcap }_{\alpha \in \mathcal{A}}{\Omega }_{\alpha }\right)}^{\circ }\ne {\mathbb{C}}^n$. 设 $\Omega$ 是它的其中一个连通分支. 实际上, 只需证明$$\mathrm{dist}({\hat{K}}_{\Omega },\partial \Omega )\ge \mathrm{dist}(K,\partial \Omega ),\forall K\subset \subset \Omega .$$对任意 $K\subset \subset \Omega ,\alpha \in \mathcal{A}$, 有$$0<d:=\mathrm{dist}(K,\partial \Omega )\le \mathrm{dist}(K,\partial {\Omega }_{\alpha })=\mathrm{dist}({\hat{K}}_{{\Omega }_{\alpha }},\partial {\Omega }_{\alpha }),$$其中最后一个等号用到了定理 1.4.13. 注意到 ${\hat{K}}_{\Omega }\subset {\hat{K}}_{{\Omega }_{\alpha }}$, 有$$\mathrm{dist}({\hat{K}}_{\Omega },\partial {\Omega }_{\alpha })\ge \mathrm{dist}({\hat{K}}_{{\Omega }_{\alpha }},\partial {\Omega }_{\alpha })\ge d.$$在左边对 $\alpha \in \mathcal{A}$ 取下确界得到 $\mathrm{dist}({\hat{K}}_{\Omega },\partial \Omega )\ge d$.

$\square$

下面的结果同样也是正确的, 但一点也不基本. 在第三章它将作为 Levi 问题解的推论出现.

定理 1.4.15 (Behnke–Stein 定理). 设 $\{{\Omega }_j\}$ 是全纯域的递增序列, 则 ${\bigcup }_{j=1}^{\infty }{\Omega }_j$ 也是全纯域.

命题 1.4.16. 令 $k>1$, 以及 ${\Omega }_j\subset {\mathbb{C}}^{n_j}(j=1,\cdots ,k)$ 是全纯域, 则 ${\Omega }_1\times \cdots \times {\Omega }_k\subset {\mathbb{C}}^{n_1+\cdots +n_k}$ 也是全纯域. 特别地, 多边形域 $\Omega ={\Omega }_1\times \cdots \times {\Omega }_k,{\Omega }_j\subset \mathbb{C}$ 是全纯域.

证明. 不失一般性, 可以假设 $k=2$. 而不难验证$${\widehat{(K\times L)}}_{{\Omega }_1\times {\Omega }_2}={\hat{K}}_{{\Omega }_1}\times {\hat{L}}_{{\Omega }_2},K\subset \subset {\Omega }_1,L\subset \subset {\Omega }_2.$$$\square$

命题 1.4.17. 设 ${\Omega }_1\subset {\mathbb{C}}^n,{\Omega }_2\subset {\mathbb{C}}^m$ 是全纯域, $f\in \mathcal{O}({\Omega }_1,{\mathbb{C}}^m)$. 则 $f^{-1}({\Omega }_2)$ 的任意连通分支都是全纯域.

证明. 设 $\Omega$ 是 $f^{-1}({\Omega }_2)$ 的一个连通分支, 而 $K\subset \subset \Omega$. 注意到 ${\hat{K}}_{\Omega }$ 是有界的, 只需要说明它在 ${\mathbb{C}}^n$ 中是闭集.
注意到 ${\hat{K}}_{\Omega }\subset {\hat{K}}_{{\Omega }_1}$, 而 ${\Omega }_1$ 是全纯域, 所以 ${\hat{K}}_{{\Omega }_1}\subset \subset {\Omega }_1$. 这导致$${\hat{K}}_{\Omega }\subset \subset {\Omega }_1.$$(1.4.3)另一方面, 首先显然有 $f({\hat{K}}_{\Omega })\subset {\widehat{f(K)}}_{{\Omega }_2}$; 而 ${\Omega }_2$ 是全纯域, 且 $f(K)\subset \subset {\Omega }_2$, 故$$f({\hat{K}}_{\Omega })\subset {\widehat{f(K)}}_{{\Omega }_2}\subset \subset {\Omega }_2.$$上面二者合起来, 得到$$f(\overline{{\hat{K}}_{\Omega }})\subset {\widehat{f(K)}}_{{\Omega }_2}\subset {\Omega }_2.$$进一步, $$\overline{{\hat{K}}_{\Omega }}\subset f^{-1}({\Omega }_2)\cap \bar{\Omega }=\Omega ,$$从而由全纯凸包的定义得到 $\overline{{\hat{K}}_{\Omega }}={\hat{K}}_{\Omega }$.

$\square$

注 1.4.18. 上述证明并未完全使用 ${\Omega }_1$ 为全纯域的条件, 而只需要 1.4.3 式对任意 $K\subset \subset \Omega$ 成立, 从而, 有下面两个结果.

命题 1.4.19. 设 ${\Omega }_1\subset {\mathbb{C}}^n$ 是开集, ${\Omega }_2\subset {\mathbb{C}}^m$ 是全纯域, $f\in \mathcal{O}({\Omega }_1,{\mathbb{C}}^m)$. 则 $f^{-1}({\Omega }_2)$ 的任意的紧包含于 ${\Omega }_1$ 的连通分支都是全纯域.

命题 1.4.20. 设 $f:{\Omega }_1\to {\Omega }_2$ 是固有全纯映射 (固有映射的含义是紧集的原像是紧集), 其中 ${\Omega }_1\subset {\mathbb{C}}^n,{\Omega }_2\subset {\mathbb{C}}^m$. 如果 ${\Omega }_2$ 是全纯域, 那么 ${\Omega }_1$ 也是.

最后我们介绍一种全纯域, 它是多圆柱的推广.

定义 1.4.21 (解析多面体). 有界开集 $\Omega \subset {\mathbb{C}}^n$ 被称为是解析多面体, 如果存在 $\bar{\Omega }$ 的邻域 $U$, 以及有限个函数 $f_1,\cdots ,f_k\in \mathcal{O}(U)$, 使得$$\Omega =\{z\in U\mid |f_j(z)|<1,j=1,\cdots ,k\}$$这一组函数 $\{f_1,\cdots ,f_k\}$ 被称为 $\Omega$ 的框架.

根据命题 1.4.19, 可以知道解析多面体的的任意连通分支都是全纯域. 下面的命题则表示每个全纯域都 “几乎” 是解析多面体.

命题 1.4.22. 设 $\Omega \subset {\mathbb{C}}^n$ 是全纯域. 则存在 $\Omega$ 的正规穷竭 $\{{\bar{\Omega }}_j\}$, 其中每个 ${\Omega }_j$ 都是解析多面体, 它们的框架都是 $\mathcal{O}(\Omega )$ 中的函数.

习题. 证明命题 1.4.22.