4.3. 与整除相关的几类环

定义 4.3.1 (元素层次上的整除概念). $A$ 是整环.

给定 $a, b \in A$ , 若有 $q \in A$ , 使得 $a = q b$ , 则称 $b$ 整除 $a$ 并记作 $b ∣ a$ .

给定 $x \in A$ , 若对任意 $a, b \in A$ , $x ∣ a \cdot b$ 意味着 $x ∣ a$ 或 $x ∣ b$ , 则称 $x$ 是素元.

给定 $y \in A$ 并假设 $y \in / A^{\times}$ (对乘法不可逆) , 假设对任意 $a, b \in A$ , 若 $y = a \cdot b$ , 则 $a \in A^{\times}$ 或 $b \in A^{\times}$ , 就称 $y$ 是不可约元.

给定 $a, b \in A$ , $a, b \in A$ , 若有 $u \in A^{\times}$ , 使得 $a = u \cdot b$ , 则称 $a$ 和 $b$ 是伴随的.

注记 4.3.2. 上述概念可在理想的层次上表述:

1)	整除性: $b ∣ a \Leftrightarrow a \in (b) \Leftrightarrow (a) \subset (b)$ ;
2)	素元: $x$ 是素元等价于 $(x)$ 是素理想.

以上叙述的证明是平凡的.

注记 4.3.3. 素元是不可约的.

实际上, 给定素元 $x$ , 若 $x = ab$ , 则 $x ∣ ab$ , 从而可不妨设 $x ∣ a$ , 即存在 $a^{'}$ , 使得 $a = a^{'} x$ , 从而, $x = a^{'} b x$ . 由于 $A$ 是整环, 所以 $a^{'} b = 1$ , 即 $b \in A^{\times}$ , 从而 $x$ 是不可约的.

我们之后会举例说明: 不可约元未必是素元.

注记 4.3.4. $A$ 是主理想整环, 则素元等价于不可约元.

只要证明不可约元为素元即可. 对任意的不可约元 $x \in A$ , 考虑 $(x)$ 以及极大理想 $m \supset (x)$ . 由于 $A$ 为主理想整环, 存在 $a \in A$ , 使得 $(a) = m \supset (x)$ . 所以, 存在 $b \in A$ , 使得 $x = ab$ . 由于 $x$ 不可约, $b \in A^{\times}$ . 这样, $m = (a) = (b^{- 1} x) = (x)$ . 特别地, 由于极大理想是素理想, $(x)$ 是素理想, 从而 $x$ 是素元.

以上推理还给出了如下命题:

命题 4.3.5. 主理想整环的非零素理想是极大理想.

注记 4.3.6.

考虑域 $K$ 上的多项式环 $K [X]$ . 由于 $K [X]^{\times} = K^{\times}$ , $P (X) \in K [X]$ 是不可约元等价于传统意义上的不可约多项式. 另外, $K [X]$ 是主理想整环, 所以对任意的不可约多项式 $P$ , $(P)$ 是极大理想, 从而 $K [X] ╱ (P)$ 是域.

考虑映射的复合: $K ⟶ \subset K [X] ⟶ π K [X] ╱ (P) .$ 这是环同态, 从而是域同态. 由此可见, 我们得到域扩张令 $d = de g (P)$ , 不妨 $P = X^{d} + a_{d - 1} X^{d - 1} + \dots + a_{1} X + a_{0}$ , 其中, $a_{i} \in K$ . 那么, $π (P) = 0$ 意味着在 $K [X] ╱ (P)$ 中, 我们有 $\overline{X}^{d} = - a_{d - 1} \overline{X}^{d - 1} - \dots - a_{1} \overline{X} - a_{0},$ 其中, $\overline{X} = π (X)$ . 据此, 我们知道 $1, \overline{X}, \dots, \overline{X}^{d - 1}$ (的 $K$ -线性组合) 生成了 $K [X] ╱ P$ . 另外, $1, \overline{X}, \dots, \overline{X}^{d - 1}$ 是 $K$ -线性无关的, 因为若有 $b_{0}, \dots, b_{d - 1} \in K$ , 使得在 $K [X] ╱ (P)$ 中, $k = 0 \sum d - 1 b_{k} \overline{X}^{k} = 0$ , 则 $k = 0 \sum d - 1 b_{k} X^{k} \in Ker (π) = (P)$ , 从而, $P$ 整除 $k = 0 \sum d - 1 b_{k} X^{k}$ . 由于 $P$ 不可约且次数为 $d$ , 从而, $k = 0 \sum d - 1 b_{k} X^{k} = 0$ , 这就证明了线性无关性.

所以, $1, \overline{X}, \dots, \overline{X}^{d - 1}$ 是一组基. 特别地, $[K [X] ╱ P : K] = de g (P)$ .

定义 4.3.7 (Euclid 整环). $A$ 是整环. 若存在映射 $N : A ⟶ Z_{⩾ 0},$ 使得 $N (0) = 0$ 并对任意的 $a, b \in A$ , 存在 (不要求唯一) $q, r \in A$ 使得 $a = q b + r$ 且要么 $r = 0$ 要么 $N (r) < N (b)$ , 则称 $N$ 是 $A$ 上的范数. 如果整环 $A$ 具有范数, 则称之为 Euclid 整环.

对于上述表达式 $a = q b + r$ , 我们称 $q$ 为 $a$ 除以 $b$ 的商, 称 $r$ 为余数.

注记 4.3.8. 在 Euclid 整环 $A$ 中有辗转相除法: 对任意 $a, b \in A$ , 存在 $r_{0}, r_{1}, \dots, r_{k}$ , 使得 $r_{0} = a, r_{1} = b, r_{0} = q_{1} r_{1} + r_{2}, r_{1} = q_{2} r_{2} + r_{3}, \dots, r_{k - 1} = q_{k} r_{k} + r_{k + 1} .$ 其中, 对 $i = 1, \dots, k$ . 由于 $N (r_{i}) < N (r_{i - 1})$ 并且 $N$ 在非负整数中取值, 从而存在 $k$ , 使得 $r_{k + 1} = 0$ .

例子 4.3.9. $Z$ 是 Euclid 整环. 对 $n \in Z$ , 我们取 $N (n) = ∣ n ∣$ .

例子 4.3.10. $K$ 是域, $K [X]$ 是多项式环, 这是 Euclid 整环.

对 $P (X) \in K [X]$ , 令 $N (P) = de g (P)$ . 由于对多项式 $F, G \in K [X]$ , 我们可以做带余除法, 使得存在唯一的 $Q, R \in K [X]$ , 满足 $G (X) = Q (X) F (X) + R (X)$ 并且 $de g (R) < de g (F)$ , 这就给出了 $K [X]$ 上的范数.

命题 4.3.11. Euclid 整环是主理想整环.

证明. 对任意理想

I \subset A

, 选取

b \in I

, 使得

N (b) = a \in I - {0} min N (a)

. 根据 Euclid 整环的定义, 对任意

a \in I

, 存在

q, r \in A

使得

a = q b + r

. 那么,

r = 0

: 否则

N (r) < N (b)

, 然而

r = a - q b \in I

, 这与

b

的范数最小矛盾. 从而,

a = q b \in (b)

. 这表明,

I = (b)

为主理想.

$□$

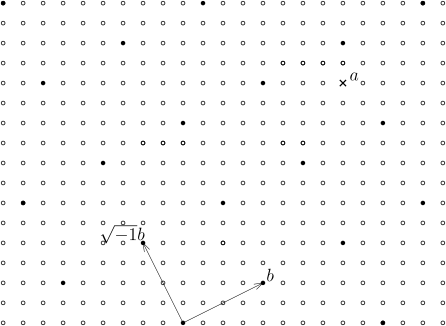
例子 4.3.12. Gauss 整数环 $Z [- 1]$ 是 Euclid 整环.

作为集合, 定义 $Z [- 1] = {a + b - 1 ∣ a, b \in Z}$ , 这是 $C$ 中整系数的格点集. 在复数的运算下, $Z [- 1]$ 是 $C$ 的子环, 从而是整环.

定义 $Z [- 1]$ 上的范数 $N : Z [- 1] ⟶ Z_{⩾ 0}, N (x + y - 1) = x^{2} + y^{2} .$ 我们还有 $N (a \cdot b) = N (a) N (b)$ .

对任意 $a = x + y - 1, b = z + w - 1 \in Z [- 1]$ , 在 $C$ 中计算其商: $\frac{a}{b} = \frac{( x z + y w ) + ( yz - x w ) - 1}{N ( b )} .$ 考虑略作修正的带余除法稍作修改: 存在 $q_{1}, q_{2} \in Z$ , $r_{1}, r_{2} \in [- \frac{1}{2} N (b), \frac{1}{2} N (b))$ , 使得 $x z + y w = q_{1} \cdot N (b) + r_{1}, yz - x w = q_{2} \cdot N (b) + r_{2} .$ 此时, $\frac{a}{b} = \frac{( x z + y w ) + ( yz - x w ) - 1}{N ( b )} = q_{1} + q_{2} - 1 + \frac{r _{1} + r _{2} - 1}{N ( b )} .$ 从而, $a = q (q_{1} + q_{2} - 1) b + r \frac{r _{1} + r _{2} - 1}{N ( b )} b = q b + r .$ 由于 $q \in Z [- 1]$ , 从而 $r \in Z [- 1]$ . 以下计算 $N (r)$ : $N (r) = N (\frac{r _{1} + r _{2} - 1}{N ( b )} b) = \frac{N ( r _{1} + r _{2} - 1 ) N ( b )}{N ( b ) ^{2}} = \frac{r _{1}^{2} + r _{2}^{2}}{N ( b )} < \frac{\frac{1}{4} N ( b ) ^{2} + \frac{1}{4} N ( b ) ^{2}}{N ( b )} < N (b) .$ 这就证明了 $N$ 为范数, 从而 $Z [- 1]$ 是 Euclid 整环.

实际上, 对于 $a, b \in Z [- 1]$ , 考虑复数 $\frac{a}{b}$ 在格点集 $Z [- 1]$ 中的位置, 那么, 存在 $q \in Z [- 1]$ , 使得 $∣ Re (q) - Re (\frac{a}{b}) ∣ < \frac{1}{2}, ∣ Im (q) - Im (\frac{a}{b}) ∣ < \frac{1}{2} .$ 特别地, $N (\frac{a}{b} - q) < \frac{1}{2}$ . 那么, 令 $r = a - q b$ . 我们就有 $N (r) = N (b) N (\frac{a}{b} - q) < \frac{1}{2} N (b) = N (b) .$

还可以几何地考虑上述带余除法: 给定 $b$ , 考虑 $C$ 上的格点集 $Γ_{(b, b)} = {n \cdot b + m \cdot - 1 b = (n + m - 1) b ∣ n, m \in Z} .$ 此时, 我们在 $Γ_{(b, b)}$ 中找一个离 $a$ 最近的格点即可 (每个格子都是正方形) .

定义 4.3.13 (唯一分解整环). $A$ 是整环. 对任意的 $a \in A - ({0} \cup A^{\times})$ , 有

1)	存在 $n ⩾ 1$ 和 $A$ 中不可约元 $p_{1}, \dots, p_{n}$ (可重复) , 使得 $a = p_{1} \dots p_{n}$ ;
2)	以上分解在伴随意义下唯一: 若 $a = q_{1} \dots q_{m}$ , $m ⩾ 1$ 且 $q_{1}, \dots, q_{m}$ 是不可约元, 则 $m = n$ 且通过调整脚标, 对任意的 $i$ , $q_{i}$ 与 $p_{i}$ 伴随.

注记 4.3.14. $Z$ 是唯一分解整环并且素因数分解在伴随意义下唯一: 比如对任意的素数 $p, q$ , 有 $p \cdot q = (- p) \cdot (- q)$ , 这里, $Z^{\times} = {1, - 1}$ .

注记 4.3.15. $K$ 是域, 多项式环 $K [X]$ 也是唯一分解整环, 这对应着多项式分解为不可约多项式的乘积.

注记 4.3.16. $A$ 是唯一分解整环, 那么, 每个 $a \in A$ 可以写成: $a = u p_{1}^{d_{1}} p_{2}^{d_{2}} \dots p_{n}^{d_{n}},$ 其中, $p_{1}, \dots, p_{d}$ 是不可约元, $u \in A^{\times}$ . 特别地, 元素之间的整除性可从分解中不可约元素的幂读出: 即对 $a = u p_{1}^{d_{1}} p_{2}^{d_{2}} \dots p_{n}^{d_{n}}, b = v p_{1}^{e_{1}} p_{2}^{e_{2}} \dots p_{n}^{e_{n}},$ 其中, $u, v \in A^{\times}$ , $p_{i}$ 为不可约元且 $d_{i}, e_{i}$ 为非负整数, $a ∣ b$ 等价于 $d_{i} ⩽ e_{i}$ , 其中 $i = 1, \dots, n$ .

注记 4.3.17. 唯一分解整环中元素为素元等价于它是不可约的.

已知素元不可约, 现在证明不可约元 $x \in A$ 是素元, 即证 $(x)$ 是素理想. 对任意 $a, b \in A, ab \in (x)$ , 即有 $c \in A$ , 使得 $ab = c x$ . 不妨设 $a, b \in / A^{\times}$ , 考虑它们的分解 $a = u p_{1} \dots p_{n}, b = v q_{1} \dots q_{m}$ , 其中, $p_{i}, q_{j}$ 为不可约元. 对 $c$ 和 $x$ 也做类似分解, 根据分解的唯一性以及 $ab = c x$ , $x$ (不可约元) 与某个 $p_{i}$ 或 $p_{j}$ 伴随, 不妨假设 $p_{1} = w x$ , 其中, $w \in A^{\times}$ , 那么 $a = u \cdot w \cdot x \cdot p_{2} \dots p_{n} \in (x) .$ 这说明 $(x)$ 是素理想.

定理 4.3.18. 主理想整环是唯一分解整环.

证明. 任选 $a \in A$ , 其中, $a \in / {0} \cup A^{\times}$ , 我们来构造 $a$ 的分解.

若 $a$ 不可约, 则 $a = a$ 为所要的分解.

否则, 有 $a = a_{1} \cdot b_{1}$ , 其中 $a_{1}, b_{1} \in / A^{\times}$ . 特别地, $(a) \subset (a_{1})$ . 若 $a_{1}, b_{1}$ 都是不可约的, 那么 $a = a_{1} \cdot b_{1}$ 为所求. 若不然, 将 $a_{1}$ 和 $b_{1}$ 分解成为乘积 $a_{2} \cdot a_{2}^{'}$ 和 $b_{2} \cdot b_{2}^{'}$ , 则有 $a = a_{2} \cdot a_{2}^{'} \cdot b_{2} \cdot b_{2}^{'}$ . 特别地, 我们有 $(a_{1}) \subset (a_{2})$ ; 然后对 $a_{2}, a_{2}^{'}, b_{2}, b_{2}^{'}$ 进行同样的讨论, 以此类推. 如果上述构造在有限步即停止, 我们就得到了 $a$ 的分解. 否则, 我们得到了无限长的主理想序列: $(a) \subset (a_{1}) \subset (a_{2}) \subset \dots \subset A,$ 并且 $(a_{i}) \neq = (a_{i + 1})$ . 令 $I = i ⩾ 1 ⋃ (a_{i})$ , 这是 $A$ 的理想. 由于对任意的 $i$ , $1 \in / (a_{i})$ , 所以 $I \neq = A$ . 根据 $A$ 是主理想整环, $I = (c)$ . 根据定义 $I$ 的构造, 存在 $k$ , 使得 $c \in (a_{k})$ , 则 $I = (a_{k})$ . 这说明该理想序列有限, 矛盾.

最终证明分解的唯一性:

a = u p_{1} \dots p_{n} = v q_{1} \dots q_{m}

是两个分解, 其中,

u, v \in A^{\times}

而

p_{i}

和

q_{j}

都是不可约元. 那么,

q_{1} \dots q_{m} \in (p_{1})

. 我们知道主理想整环中的不可约元是素元, 所以,

(p_{1})

是素理想. 从而, 存在某个

q_{j} \in (p_{1})

, 比如说

q_{1} \in (p_{1})

,

q_{1} = w p_{1}

. 由于

q_{1}

不可约, 则

w \in A^{\times}

. 从而,

u p_{2} \dots p_{n} = v w \cdot q_{2} \dots q_{m} .

如此继续下去, 唯一性是明显的.

$□$

注记 4.3.19. 我们已经证明了如下包含关系: ${Euclid 整环} \subset {主理想整环} \subset {唯一分解整环} .$ 并且在以上三种情形下某元素为素元等价于它是不可约的.

例子 4.3.20. $A = Z [- 5]$ 不是唯一分解整环.

作为集合, $Z [- 5] = {x + y - 5 ∣ x, y \in Z}$ , 它上面的运算为复数的四则运算. 特别地, 这是 $C$ 的子环.

在 $A = Z [- 5]$ 上, 我们有分解: $6 = 2 \times 3 = (1 + - 5) (1 - - 5) .$ 我们证明 $2, 3, 1 \pm - 5$ 是不可约的且它们两两不伴随. 我们考虑如下的范数映射: $N : Z [- 5] \to Z, x + y - 5 \mapsto x^{2} + 5 y^{2} .$ 对任意的 $a, b \in A$ , 我们有 $N (a \cdot b) = N (a) N (b)$ . 特别地, 如果 $a \in A^{\times}$ , 令 $b = a^{- 1}$ , 则 $N (a) N (b) = N (1) = 1.$ 由于 $N (a)$ 和 $N (b)$ 是非负整数, 所以 $N (a) = 1$ , 从而, $A^{\times} = {\pm 1}$ . 对以上计算稍加分析即可得出 $N (a) = 1 \Leftrightarrow a \in A^{\times} .$ 另外, 我们观察到 $N (2) = 4, N (3) = 9, N (1 \pm - 5) = 6$ 并且 $2, 3 \in / N (Z [- 5])$ , 所以 $2, 3, 1 \pm - 5$ 是不可约的. 另外, 不存在 $u \in A^{\times}$ , 使得 $u (1 + - 5) = 1 - - 5$ . 所以, 以上元素两两不伴随. 所以, $Z [- 5]$ 不是唯一分解整环.

例子 4.3.21 (Gauss 整数环的应用: Fermat 的定理).

我们已经证明了 $Z [- 1]$ 是 Euclid 整环, 其范数为 $N : Z [- 1] ⟶ Z_{⩾ 0}, N (x + y - 1) = x^{2} + y^{2} .$ 另外, 对任意 $a, b \in Z [- 1]$ , $N (a \cdot b) = N (a) N (b)$ . 从而, 借助范数 $N$ , 我们可以计算 $Z [- 1]^{\times}$ : $a \in Z [- 1]^{\times}$ 等价于 $N (a) = 1$ . 所以, $Z [- 1]^{\times} = {\pm 1, \pm - 1} .$ 根据 $N (a \cdot b) = N (a) N (b)$ 以及 $Z [- 1]^{\times} = N^{- 1} (1)$ , 若 $p \in Z$ 是素数, $a \in Z [- 1]$ 使得 $N (a) = p$ , 则 $a$ 是 $Z [- 1]$ 的不可约元 (等价于素元) .

我们要刻画 $Z [- 1]$ 的不可约元, 这是主理想整环, 只要刻画 $Z [- 1]$ 中素理想即可. 假设 $p \subset Z [- 1]$ 是 (非零) 素理想, $Z \subset Z [- 1]$ 是子环, 我们考虑 $p \cap Z$ 是 $Z$ 的非零素理想:

•

对任意的 $x + y - 1 \in p - {0}$ , 我们有 $x^{2} + y^{2} = (x - y - 1) (x + y - 1) \in p \cap Z$ , 从而, $p \cap Z \neq = 0$ .

•

$p \cap Z$ 是素理想.

我们对环同态环同态 $Z ↪ Z [- 1]$ 应用如下命题: ¹对任意环同态 $φ : A \to B$ , $p \subset B$ 是理想, 则 $φ^{- 1} (p) \subset A$ 也是理想并且若 $p$ 是素理想, 则 $φ^{- 1} (p)$ 亦然.

由于 $Z$ 是主理想整环, 所以存在素数 $p$ , 使得 $p \cap Z = (p)$ . 所以, 每个 $Z [- 1]$ 的素理想都与某个 $Z$ 中的素数相关联. 下面交换图概括了上述分析:

由于 $N (p) = p^{2}$ 并且 $p^{2}$ 在 $Z$ 中分解方式只有 $p^{2} = 1 \cdot p^{2} = p \cdot p$ 两种, 根据 $N (ab) = N (a) N (b)$ , 作为 $Z [- 1]$ 中的元素, 仅有两种可能:

•	第一, $p$ 在 $Z [- 1]$ 中仍不可约;
•	第二, $p$ 在 $Z [- 1]$ 中恰可写成两个不可约元之积.

我们现在判断 $(p) \subset Z [- 1]$ 是否是素理想, 这等价于研究 $Z [- 1] ╱ p Z [- 1] = Z [- 1] ╱ (p)$ 是否是整环. 通过复合映射 $Z \to Z [- 1] \to Z [- 1] ╱ p Z [- 1]$ 以及环同态的基本定理, 我们得到环同态 $F_{p} = Z ╱ p Z ⟶ Z [- 1] ╱ p Z [- 1] .$ 我们考虑环同态 $φ : F_{p} [X] ⟶ Z [- 1] ╱ p Z [- 1], P (X) \mapsto P (- 1) .$ 由于 $φ (X^{2} + 1) = 0$ , 根据环同态的基本定理, 我们得到 $ψ : F_{p} [X] ╱ (X^{2} + 1) ⟶ ≃ Z [- 1] ╱ p Z [- 1] .$ 这很明显是满射. 另外, $F_{p} [X] ╱ (X^{2} + 1)$ 有 $p^{2}$ 个元素; 通过研究 Gauss 整数对应的格点我们知道 $Z [- 1] ╱ p Z [- 1]$ 也恰有 $p^{2}$ 个元素, 所以 $φ$ 是环同构.

综合以上讨论, $(p) \subset Z [- 1]$ 是素理想等价于 $F_{p} [X] ╱ (X^{2} + 1)$ 是整环. 我们有两种可能性:

•

$X^{2} + 1$ 是 $F_{p} [X]$ 中的不可约多项式. 此时, $(X^{2} + 1) \subset F_{p} [X]$ 是素理想, 所以 $F_{p} [X] ╱ (X^{2} + 1)$ 是整环. 此时, $p$ 是 $Z [- 1]$ 的素元.

•

$X^{2} + 1$ 在 $F_{p} [X]$ 中可约. 此时必然有 $X^{2} + 1 = (X + a) (X - a)$ , 其中 $a^{2} = - 1$ 且 $a \in F_{p}$ . 这等价于 $- 1 \in F_{p}$ 是完全平方 (若 $- 1$ 不是完全平方, 该 $X^{2} + 1$ 不可约) . 另外, 理想 $(X - a)$ 与 $(X + a)$ 互素 (因为 $(X - a) + (X + a) = F_{p} [X]$ ) , 根据中国剩余定理, $F_{p} [X] ╱ (X^{2} + 1) ≃ F_{p} [X] ╱ (X + a) \times F_{p} [X] ╱ (X - 1) .$ 这不是整环 (因为 $(1, 0) \cdot (0, 1) = (0, 0)$ ) , 从而 $p$ 不是 $Z [- 1]$ 的素元.

总之, 素数 $p$ 在 $Z [- 1]$ 中不可约当且仅当 $- 1$ 不是 $Z ╱ p Z$ 中的完全平方.

这是初等数论中标准的二次剩余问题: 假设 $ξ$ 是循环群 $F_{p}^{\times}$ 的生成元, 则 $- 1 = ξ^{d}$ , 其中 $0 ⩽ d < p - 1$ . 特别地, $2 d < 2 (p - 1)$ . 由于 $ξ^{2 d} = 1$ (因为 $(- 1)^{2} = 1$ ) , 所以 $p - 1∣2 d$ . 根据 $2 d < 2 (p - 1)$ , $2 d = p - 1$ , 即 $d = \frac{p - 1}{2}$ . 我们分情况讨论:

•	$p = 2$ . 此时, $- 1 = 1 \in Z ╱ 2 Z$ 是完全平方.
•	$p \equiv 1 mod 4$ , 即 $p = 4 k + 1$ . 此时, $- 1 = ξ^{\frac{p - 1}{2}} = ξ^{2 k}$ 是完全平方.
•	$p \equiv 3 mod 4$ , 即 $p = 4 k + 3$ . 此时, $- 1 = ξ^{\frac{p - 1}{2}} = ξ^{2 k + 1}$ . 如果 $- 1 = b^{2} = ξ^{2 l}$ 是完全平方, 则 $ξ^{2 k + 1} = ξ^{2 l}$ , 即 $ξ^{2 k + 1 - 2 l} = 1$ , 从而 $p - 1 ∣ 2 k + 1 - 2 l$ . 然而 $p - 1$ 是偶数, 矛盾. 所以, $- 1$ 不是完全平方.

综上所述, 只有满足 $p \equiv 3 mod 4$ 的素数 $p$ 在 $Z [- 1]$ 中仍为不可约的.

当 $p \equiv 1 mod 4$ 时, 我们有 $p = (x + y - 1) (z + w - 1), x, y, z, w \in Z .$ 其中, $x + y - 1 ， z + w - 1$ 是 $Z [- 1]$ 中的不可约元素. 另外, 我们必然有 $N (x + y - 1) = p \Rightarrow x^{2} + y^{2} = p \Rightarrow p = (x + y - 1) (x - y - 1) .$ 根据 $Z [- 1]$ 的唯一分解, $z + w - 1 \in {\pm, \pm - 1} \cdot x - y - 1$ . 这就给出了 Fermat 的著名结果: 素数 $p$ 可写成两个完全平方数之和 $x^{2} + y^{2}$ 当且仅当 $p \equiv 1 mod 4$ . 进一步, $p = x^{2} + y^{2}$ 的写法是唯一的.

另外, 交换图表给出了 $Z [- 1]$ 中所有不可约元 (在伴随意义下) ${1 + - 1, x \pm y - 1, q ∣ ∣ q \equiv 3 mod 4 是素数; q \equiv 3 mod 4 是素数且 x^{2} + y^{2} = 1, x > 0, y > 0} .$

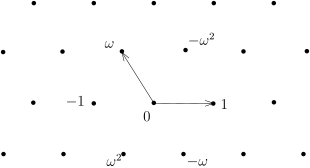
例子 4.3.22 (Eisenstein 整数环及其应用: $n = 3$ 时的 Fermat 大定理). 令 $ω = e^{\frac{2 π}{3} i}$ . 作为集合, 定义 Eisenstein 整数为 $Z [ω] = {a + bω ∣ a, b \in Z}$ , 这是 $C$ 上的正三角形的格点集:

根据 $ω^{2} + ω + 1 = 0$ , 在复数的运算下 $Z [ω]$ 是 $C$ 的子环, 从而是整环.

定义 $Z [ω]$ 上的范数 $N : : Z [ω] ⟶ Z_{⩾ 0}, N (a + bω) = ∣ a + bω ∣^{2} .$ 实际上, 我们有 $N (a + bω) = a^{2} - ab + b^{2} = \frac{1}{4} ((2 a - b)^{2} + 3 b^{2}) \in Z_{⩾ 0} .$ 在 $Z [ω]$ 中, 范数最小的非零元素为 ${\pm 1, \pm ω, \pm ω^{2}}$ , 其余非零元素的范数至少是 $3$ . 根据 $N (x \cdot y) = N (x) N (y)$ , 我们就可以断言 $Z [ω]^{\times} = {\pm 1, \pm ω, \pm ω^{2}} ≃ Z ╱ 6 Z .$ 我们现在证明 $Z [ω]$ 在范数 $N$ 下是 Euclid 整环: 注意到以每个格点为中心放置一个半径为 $1$ 的开圆盘就可以覆盖整个复平面 $C$ , 从而, 对任意的 $z \in C$ , 存在 $q \in Z [ω]$ , 使得 $∣ z - q ∣ < 1$ . 对任意的 $a, b \in Z [ω]$ , 则存在 $q \in Z [ω]$ , 使得 $∣ q - \frac{a}{b} ∣ < 1 \Leftrightarrow ∣ a - b q ∣ < ∣ b ∣.$ 令 $r = a - b q \in Z [ω]$ , 则 $a = q \cdot b + r$ 并且 $N (r) < N (b)$ . 这就证明了 $Z [ω]$ 是 Euclid 整环. ²

在 $Z [ω]$ 中, $1 - ω$ 是素元 (因为其范数为 $3$ ) . 另外, 范数为 $3$ 的元素共有 $6$ 个, 它们为 $Z [ω]^{\times} \cdot (1 - ξ)$ . 尽管 $3$ 在 $Z$ 中是素数, 但是它在 $Z [ω]$ 中可以分解: 通过 $N (3) = 9$ , 我们不难猜到 $3 = (1 - ω) (1 - \overline{ω}) = (1 - ω) (1 - ω^{2}) = u (1 - ω)^{2}, u \in Z [ω]^{\times} .$

利用 $Z [ω]$ 中的唯一分解定理, 我们来证明方程 $x^{3} + y^{3} = z^{3}$ 的整数解必然满足 $x yz = 0$ .

用反证法, 假设 $x, y, z$ 均非零. 不妨假设 $x, y, z$ 两两互素 (否则可以通过约掉公因子化为此情形) . 注意到 $x, y$ 在 $Z$ 中互素, 那么必然在 $Z [ω]$ 中互素, 因为 $(x) + (y)$ 已经包含了元素 $1$ . 由于整数的三次方除 $9$ 的余数必然是 $0$ 或 $\pm 1$ , 所以, $x, y, z$ 中必有某个数被 $3$ 整除. 通过将方程变形为 $x^{3} + (- z)^{3} = (- y)^{3}$ , 总可假设 $3 ∣ z$ . 特别地, $3 ∣ x + y$ (因为 $3 ∣ x^{3} + y^{3}$ 意味着 $x, y$ 除 $3$ 一个余数为 $1$ 而另一个余数为 $- 1$ ) . 所以, 我们只要研究如下方程的非零整数解即可: $x^{3} + y^{3} = (3^{k} z)^{3}, k ⩾ 1 且 3 ∤ z, \dots \dots (*)$ 我们可以将该方程分解为 $(x + y) (x + ω y) (x + ω^{2} y) = (3^{k} z)^{3} .$ 由于 $3 ∣ x + y$ , 所以, $1 - ω ∣ x + y$ . 由于 $x + y - (x + ω y) = (1 - ω) y$ , 所以, $1 - ω ∣ x + ω y$ ; 类似的, $1 - ω ∣ x + ω^{2} y$ . 所以, $1 - ω$ 是 $x + y, x + ω y$ 和 $x + ω^{2} y$ 的共约数. 实际上, 它还是最大公约数: 对任意的公约数 $w$ , 有 $w ∣ (x + ω y) - (x + y) = (1 - ω) y, w ∣ (x + ω y) - ω (x + y) = (1 - ω) x .$ 由于 $x$ 与 $y$ 在 $Z [ω]$ 中互素, 所以, $w ∣ 1 - ω$ . 实际上, 这个证明表明 $x + y, x + ω y$ 和 $x + ω^{2} y$ 中任两个数的最大共约数均为 $1 - ω$ .

利用 $3 = (1 - ω) (1 - ω^{2})$ 并且 $1 - ω$ 与 $1 - ω^{2}$ 伴随, 我们将 $(*)$ 写成 $(x + y) \cdot \frac{x + ω y}{1 - ω} \cdot \frac{x + ω ^{2} y}{1 - ω ^{2}} = 3^{3 k - 1} z^{3},$ 其中, 以上每一个项都是 Eisenstein 整数并且左边三项两两互素 (注意到 $(1 - ω)^{2} ∣ x + y$ , 从而, $x + ω y$ 与 $x + ω^{2} y$ 中恰含一个 $1 - ω$ 的因子) . 由于 $3 ∣ x + y$ , 根据唯一分解定理, 所以 ${x + y = 3^{3 k - 1} w^{3}, x + ω y = (a + bω)^{3},$ 其中, $a, b \in Z$ 而 $w \in Z [ω]$ . 由于 $w^{3} \in Q \subset R$ , 通过考察 $w$ 的幅角, $w$ 落在过原点 $0$ 和 $1, ω$ 或 $ω^{2}$ 的直线上. 通过对 $w$ 乘 $ω$ 或 $ω^{2}$ , 不妨假设 $w \in R$ , 从而, $w \in R \cap Z [ω] = Z$ . 所以, 我们还可要求上面式子中的 $w \in Z$ . 另外, 我们注意到 $3 ∤ w$ .

利用 $ω^{2} = - ω - 1$ , 我们计算 $x + ω y = (a + bω)^{3} = (a^{3} + 3 a^{b} - 6 a b^{2} + b^{3}) - (a^{3} + 3 a b^{2} - 6 a^{2} b + b^{3}) .$ 所以, ${x = a^{3} + 3 a^{2} b - 6 a b^{2} + b^{3}, y = - a^{3} - 3 a b^{2} + 6 a^{2} b - b^{3} .$ 从而, $3^{3 k - 1} w^{3} = x + y = 9 ab (a - b) \Leftrightarrow ab (a - b) = (3^{k - 1} w)^{3} .$ 其中, 上面式子左右两边每一项均为整数. 由于 $x, y$ 互素, 所以, $a, b$ 互素, 从而 $a, b, a - b$ 两两互素 (特别地, $a, b, a - b$ 均非零) . 考虑 $(a, b, a - b, w) \to (a - b, - b, a, - w)$ 或者 $(a, b, a - b, w) \to (b - a, - a, b, w)$ , 根据整除与互素关系, 我们不妨假设 $a = (3^{k - 1} z^{'})^{3}, b = (x^{'})^{3}, a - b = (y^{'})^{3},$ 其中, $x^{'}, y^{'}, z^{'} \in Z$ 且非零. 所以, $(x^{'})^{3} + (y^{'})^{3} = (3^{k - 1} z^{'})^{3}, 且 3 ∤ z^{'} .$ 以上, $3 ∤ z^{'}$ 是因为 $3 ∤ w$ . 与 $(*)$ 做比较, 我们总可以一直进行上述操作来降低 $k$ , 最终得到 $(*)$ 中 $k = 0$ , 这与先前讨论的 $3 ∣ x yz$ 矛盾.

1.	^ 证明请参考练习题 4.6.6, 6. 和 7.
2.	^ 同样的想法也可以用来证明 Gauss 整数环 $Z [- 1]$ 是 Euclid 整环.

名字空间

视图

4.3. 与整除相关的几类环