作业: Fourier 级数几乎处处发散的 函数
Gibbs 现象, Fourier 级数
A1) | 试构造数列 , 使得它在 上稠密却不是等分布的. |
A2) | 对任意的 , 证明, 卷积在频率空间来看就是正常的乘积: |
A3) | 是 上以 为周期的实值函数, 它在 上是有界的单调函数. 证明, 存在常数 , 使得对任意的 , 我们都有(先证明 上有界的单调函数可以被形如 的函数逼近, 其中 , ) |
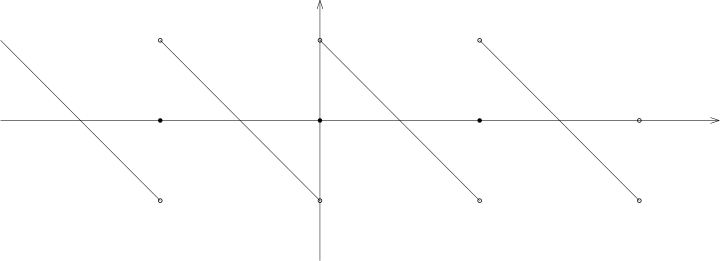
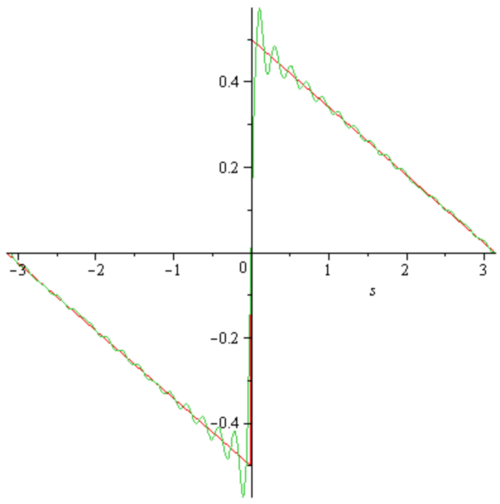
A4) | (Gibbs 现象) 我们定义墙头草形状的以 为周期的函数 , 其中, 当 时, 我们有 此时, 在间断点 处, 我们有 . 证明, 的 Fourier 级数可以写为 证明, 对于部分和 , 我们有这是分段 函数在第一类间断点处 Fourier 系数收敛的典型行为, Fourier 级数在间断点处起伏的最大值接比间断本身 () 要大 . |
A5) | 假设 , 证明, 级数是绝对收敛的. |
A6) | 我们定义级数证明, 是 上以 为周期的光滑函数. 利用证明, |
一个含参数积分的研究
B1) | 证明, 对任意的 , 如下积分是良好定义的: |
B2) | 证明, 是 的连续函数. |
B3) | 证明, 是可导的. |
B4) | 试计算 . |
B5) | 证明, 对 , 如下的积分是发散的: |
B6) | 证明, 对任意的 , 如下在 Riemann 意义下的反常积分是良好定义的: 即 存在. |
B7) | 证明, 是 的连续函数. |
B8) | 试计算 . |
Laplace 变换的基本性质
C1) | 假设 是 上定义的 Lebesgue 可积函数. 我们定义它的 Laplace 变换为: 其中 . 证明, 是 的函数. |
C2) | 证明, 对任意的 , 我们都有 |
C3) | 假设 和 是 上定义的 Lebesgue 可积函数, 我们定义它们的 “卷积” 为证明, . |
C4) | 假设 和 是 上定义的 Lebesgue 可积函数. 证明, |
Fourier 级数几乎处处发散的 -函数
注记. 1922 年, Kolmogorov (19 岁, 还在莫斯科大学读本科) 在论文 Une série de Fourier-Lebesgue divergente presque partout 中构造一个 函数, 这个函数的 Fourier 级数的部分和几乎处处是发散的. 这个问题的目的就是重现这个著名反例的构造.
先固定一个自然数 (在接下来的过程中它会变化) . 我们任意选取 个正的奇数 (我们将在接下来的过程中确定它们的大小) . 定义如下的数组, 函数和区间:
• | . 我们令 , 并且归纳地定义 . |
• | , 其中 . |
• | , 其中区间 . |
• | 对于 , 我们定义区间 . |
根据 Dirichlet 核函数的基本性质, 我们知道 Fourier 级数的部分和可以由下面的公式计算: 仿照这个形式, 我们定义
K1) | 证明, | ||||||||
K2**) | 证明, . (提示: 可以参考关于有界变差函数的 Fourier 级数的 Jordan 定理的证明过程) | ||||||||
K3*) | 证明, 我们可以归纳地选取 (足够大的) 正奇数 , 使得区间 两两不相交并且对任意的 和任意的 , 我们都有(提示: 如果 已经选择好了, 那么我们通过 的选择就可以使得 足够大) | ||||||||
K4) | 证明, Dirichlet 核函数 满足 | ||||||||
K5) | 证明, 当 的时候, 对任意的 , 我们可以将 写成并且我们有如下的控制: . | ||||||||
K6) | 证明, 对任意的 , 我们都有 | ||||||||
K7) | 证明, 对任意的 , 我们有 | ||||||||
K8) | 证明, 如果 , 对任意的 , 我们有 | ||||||||
K9) | 证明, 如果 选取的足够大, 那么如下集合的 Lebesgue 测度满足 | ||||||||
K10) | 我们定义证明, . | ||||||||
K11) | 证明, 对任意的 和 , 我们都有 | ||||||||
K12) | 证明, 存在以 为周期的函数列 , 使得
(提示: 选取 即可) | ||||||||
K13) | 证明, 存在以 为周期的函数列 , 子区间序列 , 正整数序列 以及单调上升的正数序列 , 使得
(提示: 选取上面的题目中的函数的子序列) | ||||||||
K14) | 利用上一个小题的结论, 我们构造证明, 在 中是良好定义的并且这个级数对几乎处处的 都收敛. | ||||||||
K15) | 证明, 的 Fourier 变换的部分和可以写成 | ||||||||
K16) | 证明, 对任意的 , 都存在一个 , 使得 . | ||||||||
K17) | 证明, 对任意的 , 我们都有 . | ||||||||
K18) | 证明, . (提示: 把 Dirichlet 核函数用它的最大值来控制) | ||||||||
K19) | 证明, 对几乎处处的 , 都发散. | ||||||||
K20) | 证明, . 注记. Lennart Carleson 在 1965 年证明了一个著名的定理, 这个定理完整地解决了 Lusin 猜想: 如果 , 那么 几乎处处收敛到 . 这一项工作是 Carleson 获得了 Wolf 奖和 Abel 奖的最主要贡献之一. Lusin 是 Kolmogorov 在莫斯科读大学时数学分析的老师. |
寄语. The purpose of computing is insight, not numbers.
—— Richard Hamming