分布的操作
在微积分的学习中, 我们可以对一个函数做特定的操作, 比如可以把一个函数限制到比较小的定义域上、可以对一个函数求导数、两个函数可以相乘等等. 我们现在讨论如何对分布做一些特定的操作.
分布的限制
假设 Ω′⊂Ω 是开子集, 那么, 我们可以定义限制映射Res:D′(Ω)→D′(Ω′),u↦Res(u).其中, 对于每个 φ∈D(Ω′), 它自然可以看作是 D(Ω) 中的元素, 从而, 我们可以要求⟨Res(u),φ⟩=⟨u,φ⟩.为了方便起见, 除了个别场合, 我们总是用 u 来直接表示 Res(u).
求偏导数
我们先考虑一个足够光滑的函数, 比如说, u∈C1(R). u 和 u′ 都是局部可积分的函数, 我们可以把它们视作是分布. 通过分部积分, 我们有⟨u′,φ⟩=∫Ru′(x)φ(x)dx=−∫Ru(x)φ′(x)dx=−⟨u,φ′⟩.这个计算启发我们: 对于 u∈D′(R), 我们可以用下面的等式来定义它的导数: ⟨u′,φ⟩:=−⟨u,φ′⟩.
假设 Ω⊂Rn 是有界开集, 给定 u∈D′(Ω), 对于任意的多重指标 α, 我们定义⟨∂αu,φ⟩=(−1)∣α∣⟨u,∂αφ⟩.
我们必须说明
∂αu 定义了
Ω 上的分布: 根据分布的定义, 对任意的紧集
K⊂Ω, 存在非负整数
p 和正常数
C (
p 和
C 依赖于
K) , 使得对任意的
φ∈CK∞(Ω), 都有
∣⟨∂αu,φ⟩∣=∣⟨u,∂αφ⟩∣⩽C∣β∣⩽psup∥∂β∂αφ∥L∞(K)⩽C∣γ∣⩽p+∣α∣sup∥∂γφ∥L∞(K).这表明我们对任意的分布都可以求导数, 即对任意的多重指标
α, 我们有 (连续) 线性映射:
∂α:D′(Ω)→D′(Ω).我们研究两个经典的例子:
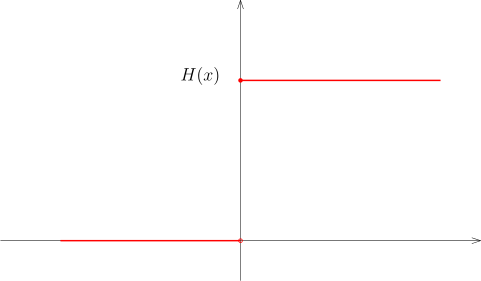
我们定义 Heaviside 函数H(x)=1x⩾0.
直观上, 这个函数在
0 之外的导数是
0, 在
0 处函数有很大的跳跃, 导数应该是无穷大. 我们证明
H(x)′=δ0.按照定义, 我们有
⟨H′(x),φ(x)⟩=−⟨H(x),φ′(x)⟩=−∫0∞φ′(x)dx=−(φ(∞)−φ(0))=φ(0)=⟨δ0,φ⟩. 我们考虑 R 上的 log 函数, 注意到log∣x∣∈Lloc1(R).我们证明, 作为分布, 有(log∣x∣)′=D′vpx1.实际上, ⟨(log∣x∣)′,φ⟩=−ε→0lim(∫−∞−εφ′log∣x∣dx+∫ε∞φ′log∣x∣dx)=ε→0lim(φ(−ε)log(ε)+∫−∞−εx1φdx−φ(ε)log(ε)+∫ε∞x1φdx).我们注意到φ(−ε)−φ(ε)=O(ε).所以, ε→0limφ(−ε)log(ε)−φ(ε)log(ε)=0.从而, ⟨(log∣x∣)′,φ⟩=ε→0lim(∫−∞−εx1φdx+∫ε∞x1φdx)=⟨vpx1,φ⟩.
我们计算 R 上的 Dirac 函数 δa 的导数, 其中 a∈R. 任给 φ∈D(R), 我们有⟨δa′,φ⟩=−⟨δa,φ′⟩=−φ′(a).
C∞(Ω)-模结构
对光滑函数 f∈C∞(Ω) 和分布 u∈D′(Ω), 我们可以定义它们的乘积 f⋅u:⟨f⋅u,φ⟩:=⟨u,fφ⟩.其中, φ 是试验函数. 由于 fφ 仍然是 D(Ω) 中的函数, 所以上面的等式是良好定义的. 为了说明 f⋅u∈D′(Ω), 要对 u 来用分布的定义: 对任意的紧集 K⊂Ω, 存在非负整数 p 和正常数 C (p 和 C 依赖于 K) , 使得对任意的 φ∈CK∞(Ω), 都有∣⟨f⋅u,φ⟩∣⩽C∣α∣⩽psup∥∂α(f⋅φ)∥L∞(K).根据 Leibniz 法则, 我们有∂α(f⋅φ)=β+γ=α∑∂βf⋅∂γφ.所以, ∣⟨f⋅u,φ⟩∣⩽C∣α∣⩽psupβ+γ=α∑∥∂βf∥L∞(K)∥∂γφ∥L∞(K)⩽新的常数 C′C∣β∣⩽p∑∥∂βf∥L∞(K)×∣γ∣⩽psup∥∂γφ∥L∞(K).这表明 f⋅u∈D′(Ω).
我们有x⋅vpx1=1.对任意的 φ∈D(R), 我们知道 xφ(x)∣∣x=0=0. 根据第一次作业题的 A6), 我们有⟨x⋅vpx1,φ⟩=⟨vpx1,xφ⟩∫Rx1⋅xφ(x)dx=∫R1⋅φ(x)dx.这就证明了命题.
分布的平移和变量替换
对于 x0∈Rn, 我们有如下的平移变换: τx0:Rn→Rn, x↦x+x0.对于局部可积的函数 f∈Lloc1(Rn), 我们可以定义 (这是一种特殊的变量替换) : (τx0f)(x):=f(x+x0).如果将 f 视为是分布, 对于试验函数 φ 而言, 我们有⟨f(⋅+x0),φ(⋅)⟩=∫Rnf(x+x0)φ(x)dx=∫Rnf(x)φ(x−x0)dx=⟨f(⋅),φ(⋅−x0)⟩=⟨f(⋅),(τ−x0φ)(⋅)⟩.对于一般的分布 u∈D′(Rn), x0∈Rn, 我们定义⟨τx0u,φ⟩:=⟨u,φ(x−x0)⟩.容易验证, τx0u 给出了一个分布. 实际上, 我们稍后在进行变量替换的时候, 也会给出这个命题的证明.
下面的命题给出了在分布意义下方向导数的另一个 (直观) 刻画:
给定分布 u∈D′(Rn), 给定向量 v=(v1,⋯,vn)∈Rn, 在分布意义下, 我们有t→0limtτtvu−u=D′j=1∑nvj∂ju.
证明. 按照定义, 我们有
⟨tτtvu−u−j=1∑nvj∂ju,φ⟩=⟨u,φttφ(x−tv)−φ(x)+j=1∑nvj∂jφ(x)⟩.根据带有积分余项的
Taylor
展开, 我们有
φt(x)=−j=1∑n∫01vj(∂jφ(x−tsv)−∂jφ(x))ds.由于
t 很小, 上述函数
φt(x) 的支撑集是紧的, 从而第一个等式的右边是良好定义的. 我们来证明在
D(Rn) 中, 上述
φt(x) 的极限是
0, 也就是说对任意的多重指标
α, 我们有
∂αφt(x)⟶L∞0: 根据 Lebesgue 控制收敛定理 (的推论, 积分与求导数可交换, 请参考上学期笔记) , 我们有
∥∂αφt(x)∥L∞=∥∥j=1∑n∫01vj(∂j∂αφ(x−tsv)−∂j∂αφ(x))ds∥∥L∞⩽∥∥j=1∑n∫01∣vj∣∣v∣∥∂∣α∣+2φ∥∞tds∥∥L∞.其中, 最后一步我们用到了 Lagrange 中值定理. 再次利用 Lebesgue 控制收敛定理, 上面的极限为
0. 命题得证.
给定 Rn 的两个开集 Ω1 和 Ω2, 我们假定Φ:Ω1→Ω2是微分同胚. 对任意一个 Ω2 上的局部可积的函数 f 和 Ω1 上的试验函数 φ, 根据换元积分公式, 我们有⟨Φ∗f,φ(x)⟩=∫Ω1f(Φ(x))φ(x)dx=∫Ω2f(y)φ(Φ−1(y))∣JΦ−1(y)∣dy=∫Ω2f(y)∣JΦ(Φ−1(y))∣φ(Φ−1(y))dy=⟨f,∣JΦ(Φ−1(y))∣φ(Φ−1(y))⟩.根据这个计算, 我们定义: Φ∗:D′(Ω2)→D′(Ω1), u↦Φ∗u.其中, 对于 u∈D′(Ω2) 和 φ∈D(Ω1), 我们定义 Φ∗u 如下: ⟨Φ∗u,φ(x)⟩:=⟨u,φ(Φ−1(y))∣JΦ−1(y)∣⟩=⟨u,∣JΦ(Φ−1(y))∣φ(Φ−1(y))⟩.为了证明 Φ∗u 的确定义了 Ω1 上的一个分布, 我们利用定义: 对任意的紧集 K⊂Ω, 存在非负整数 p 和正常数 C (p 和 C 依赖于 K) , 使得对任意的 φ∈CK∞(Ω), 都有∣⟨Φ∗u,φ⟩∣⩽C∣α∣⩽psup∥∥∂α(∣JΦ(Φ−1(y))∣φ(Φ−1(y)))∥∥L∞(K).我们需要利用链式法则多次求导数. 重要的观察是上述导数最多给出 φ 的不超过 p 次的导数的线性组合, 其中, 这些线性系数都是 Φ(y) 的不超过 p+1 阶的导数的多项式. 由于我们限制在紧集 K 上, 所以这些系数是一致有界的 (这个界可能依赖于 K) , 从而, 通过改变一下上面不等式中的常数 C, 我们最终得到∣⟨Φ∗u,φ⟩∣⩽C′∣α∣⩽psup∥∂αφ∥L∞(K).
因为在光滑函数情况下, Φ∗u 就是函数的复合, 我们还把上面的拉回映射写成u∘Φ=Φ∗u.
给定微分同胚
Φ:Ω1→Ω2, 它把
Ω2 上的 Dirac 函数拉回, 得到
Ω1 上的 Dirac 函数, 这给出了 Jacobi 行列式的一个精确的解释: 这是一点处体积的变化.
假设 x0∈Ω1, y0∈Ω2 并且 Φ(x0)=y0. 那么, 我们有Φ∗δy0=∣JΦ(x0)∣1δx0.实际上, 利用定义, 对于任意的 φ∈D(Ω1), 我们有⟨Φ∗δy0,φ(x)⟩=⟨δy0,∣JΦ(Φ−1(y))∣φ(Φ−1(y))⟩=∣JΦ(Φ−1(y0))∣φ(Φ−1(y0))=∣JΦ(x0)∣φ(x0).很明显, ∣JΦ(x0)∣φ(x0)=⟨∣JΦ(x0)∣1δx0,φ⟩.
给定微分同胚 Φ, 如果 u 是 C1 的函数, 我们可以对求导数运算运用链式法则:∂j(u∘Φ)=k=1∑n∂jΦk(x1,⋯,xn)⋅(∂ku∘Φ)(x1,⋯,xn).对于一般的分布 u, 我们实际上 (后来) 可以先用光滑函数逼近这个分布, 然后上面的链式法则在极限的情况下仍然成立.
我们现在给出一个直接的证明: 设 Ψ=Φ−1 是 Φ 的逆映射. 按照分布与一个微分同胚的复合的定义, 我们有⟨k=1∑n∂xj∂Φk⋅∂yk∂u∘Φ,φ⟩=k=1∑n⟨∂yk∂u∘Φ,∂xj∂Φk⋅φ⟩=k=1∑n⟨∂yk∂u,(∂xj∂Φk∘Ψ)(φ∘Ψ)∣JΨ∣⟩=−k=1∑n⟨u,∂yk∂[(∂xj∂Φk∘Ψ)(φ∘Ψ)∣JΨ∣]⟩另外, 对任意 g∈C0∞(Ω), 我们有0=∫Ω1∂xj∂(g∘Φ)dx=k=1∑n∫Ω1∂xj∂Φk⋅∂yk∂g∘Φdx=k=1∑n∫Ω2∂xj∂Φk∘Ψ⋅∂yk∂g⋅∣JΨ(y)∣dy=−k=1∑n∫Ω2g∂yk∂(∂xj∂Φk∘Ψ⋅∣JΨ(y)∣)dy根据 Lloc1(Ω) 到 D′(Ω) 嵌入的单射性, 上面的等式等价于说k=1∑n∂yk∂(∂xj∂Φk∘Ψ⋅∣JΨ(y)∣)=0.从而⟨k=1∑n∂xj∂Φk⋅∂yk∂u∘Φ,φ⟩=−k=1∑n⟨u,∂yk∂(φ∘Ψ)[(∂xj∂Φk∘Ψ)∣JΨ∣]⟩=−⟨u,∂xj∂φ∘Ψ∣JΨ∣⟩=−⟨u∘Φ,∂xj∂φ⟩.这就证明如下关于分布的链式法则: ∂j(Φ∗u)=k=1∑n∂jΦk⋅Φ∗((∂ku)).
关于分布的 Stokes 公式
我们用分布的语言来表述 Stokes 公式. 我们上个学期证明了:
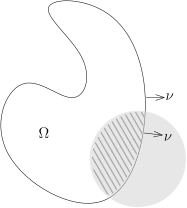
假设 Ω 是一个有界带边光滑区域, ν(x)=(ν1(x),⋯,νn(x)) 为 ∂Ω 的单位外法向量, dσ 为 ∂Ω 上的曲面测度. 对任意的 φ∈C1(Rn,C), 我们有∫Ω∂xi∂φ(x) dx=∫∂Ωφ(x)νi(x) dσ.
给定了上面 Stokes 公式中所述的
Ω, 它的边界
∂Ω 的曲面测度
dσ 在如下的意义下定义了
Rn 上一个分布:
dσ:D(Rn)→C, φ↦∫∂Ωφ(x)dσ(x).这是一个
0 阶的分布, 我们把证明的细节留给不放心的同学来验证. 类似地, 对每一个
i⩽n, 如下的公式也定义了一个分布:
νidσ:D(Rn)→C, φ↦∫∂Ωφ(x)νi(x)dσ(x).我们可以把 Stokes 公式改写成如下的形式: ⟨1Ω,∂iφ⟩=∫Rn1Ω(x)∂xi∂φ(x) dx=∫∂Ωφ(x)νi(x) dσ.所以, 用分布的语言来写, 我们有
假设 Ω 是一个有界带边光滑区域, ν(x)=(ν1(x),⋯,νn(x)) 为 ∂Ω 的单位外法向量, dσ 为 ∂Ω 上的曲面测度, 作为分布, 我们有等式∂i1Ω=D′(Rn)−νidσ.如果用向量值分布的语言 (可以望文生义地定义) 来写, 我们有∇1Ω=D′(Rn)−νdσ.
我们现在回到 1 维的情形, 此时的 Stokes 公式就是 Newton–Leibniz 公式.
对于 f(x)∈L1((a,b)), 我们定义其原函数为F(x)=∫axf(y)dy.那么, F(x) 是连续函数. 在分布的意义下, 我们有F(x)′=D′f(x).
证明. 为了证明 F 是连续的, 我们把它写成F(x)=∫[a,b]f⋅1(a,x]dμ,其中 dμ 是 Lebesgue 测度. 对任意的 xk→x, 我们知道 f⋅1(a,xk] 逐点地收敛到 f⋅1(a,x], 利用 ∣f∣ 作为控制函数, Lebesgue 控制收敛定理告诉我们k→∞limF(xk)=F(x).
我们用定义计算
F′. 对于任意的试验函数
φ∈D((a,b)), 我们有
⟨F′,φ⟩=−⟨F,φ′⟩=∫(a,b)(∫(a,b)f⋅1(a,x](y)dy)φ′(x)dx=∫∫(a,b)×(a,b)1A(x,y)f(y)φ′(x)dxdy.这里,
A={(x,y)∈(a,b)×(a,b)∣∣y⩽x} 并且我们是利用了 Fubini 定理把它化成了
2 维的积分. 再次利用 Fubini 定理, 我们先对
x 积分再对
y 积分, 就有
⟨F′,φ⟩=∫(a,b)f(y)(∫ayφ′(x)dx)dy=∫abf(y)φ(y)dy=⟨Tf,φ⟩.其中, 我们用到了
φ(a)=0 (因为
supp(φ)⊂(a,b)) . 这就是说, 在分布的意义下,
F′=f.