跳跃公式
上次课的最后利用 Fubini 定理, 我们证明了: 对于 f(x)∈L1((a,b)), 我们定义其原函数为F(x)=∫axf(y)dy.那么, F(x) 是连续函数. 在分布的意义下, 我们有F(x)′=D′f(x).
给定分布 u∈D′((a,b)), 如果在分布的意义下 u′=0, 那么, 在分布的意义下, u 为常数, 即存在 c∈C, 使得u=D′c.
证明. 我们任意选定一个 χ∈C0∞((a,b)), 使得 ∫abχ(x)dx=1. 令 c=⟨u,χ⟩.
对于任意一个试验函数
φ∈D((a,b)), 我们定义
g(x)=φ(x)−(∫−∞∞φ(y)dy)χ(x),那么, 我们有
∫Rg(x)dx=0.我们定义函数
ψ(x)=∫axg(y)dy.利用
g 的积分消失的性质, 我们容易说明 (证明支集是紧的)
ψ∈D((a,b)). 特别地, 我们可以用
ψ 作为试验函数. 由于
u′=0, 所以
0=−⟨u,ψ′⟩=−⟨u,φ(x)−(∫Rφ(y)dy)χ(x)⟩=⟨u,φ⟩−c∫Rφ(x)dx.所以,
⟨u,φ⟩=∫Rc⋅φ(x)dx=⟨c,φ⟩.这说明, 作为分布, 我们有
u=c.
综合上面的两个命题, 我们有如下的性质:
假定 f∈L1((a,b)), 那么关于分布的常微分方程u′=f在 D′((a,b)) 中所有的解均形如u=c+∫axf(y)dy,其中 c∈C 为常数.
我们现在来证明所谓的
跳跃公式:
给定连续函数 g∈C(R), 我们假设它的分布导数 g′∈Lloc1(R). 那么, 对任意的 −∞<a<b<+∞, 在分布的意义下, 我们有dxd(g(x)1(a,b)(x))=D′g′(x)1(a,b)(x)−g(b)δb+g(a)δa.
证明. 根据上一个命题, 我们有 (作为分布或者连续函数)
g(x)=g(a)+∫axg′(y)dy.按定义, 对任意的试验函数
φ, 我们还有
⟨dxd(g(x)1(a,b)(x)),φ⟩=−∫abg(x)φ′(x)dx=−g(a)∫abφ′(x)dx+∫ab[∫axg′(y)dy](−φ′(x))dx=Fubini−g(a)∫abφ′(x)dx−∫ab[∫ybφ′(x)dx]g′(y)dy=−g(a)φ(b)−φ(a)∫abφ′(x)dx−φ(b)g(b)−g(a)∫abg′(x)dx+∫abφ(y)g′(y)dy.将上面最后一行合并同类项即得.
分布与 Stokes 理论的第一个应用: Cauchy 积分公式
考虑复平面 C 上的开区域 Ω. 函数 (映射) F 在 Ω 上定义并且在 C 中取值: F:Ω→C我们假设 F 是连续可微的 (F∈C1) .
如果把 F 视作是从 Ω 到 R2 的映射, 我们通常将它写作F(z)=F(x,y)=f(x,y)+ig(x,y).我们定义微分算子:∂=∂z∂=21(∂x∂+i∂y∂).所以, ∂ 对 F 的作用为: ∂F=21(∂x∂f−∂y∂g)+2i(∂x∂g+∂y∂f).我们现在定义 F 在复解析意义下的导数 (如果极限存在的话) : F′(z0)=z→z0limz−z0F(z)−F(z0).其中, z0∈Ω 是给定的一点.
如果 F′(z) 在 Ω 上处处有定义并且是连续函数, 我们就称 F 为 Ω 上的复解析函数.
我们现在证明
函数 F:Ω→C 是复解析函数当且仅当 ∂F=0. 特别地, F(x,y)=f(x,y)+ig(x,y) 在 Ω 上是复解析的当且仅当如下的偏微分方程组在 Ω 上成立⎩⎨⎧∂x∂f−∂y∂g=0;∂x∂g+∂y∂f=0.这个方程组是所谓的 Cauchy–Riemann 方程.
证明. 假设 F 在 z0 处的复解析导数可定义, 我们令它为F′(z0)=z→z0limz−z0F(z)−F(z0)=a+bi.根据极限的定义, 当 z→z0 时, 我们有F(z)−F(z0)−F′(z0)(z−z0)=o(∣z−z0∣).把 F 看作是从 Ω 到 R2 的映射, 用映射微分的语言来写 (参考上学期第一部分内容) , 我们有F(x,y)−F(x0,y0)−(ab−ba)(x−x0y−y0)=o(∣x−x0∣+∣y−y0∣),其中 z=x+y−1, z0=x0+y0−1. 这表明矩阵 (ab−ba) 是映射 F 在 (x0,y0) 处的微分, 从而是这个映射在这个点处的 Jacobi 矩阵. 所以, (ab−ba)=Jacobi 矩阵=(∂x∂f∂x∂g∂y∂f∂y∂g).比较系数, 我们有∂x∂f=a=∂y∂g=0, ∂x∂g=b=−∂y∂f=0.所以, Cauchy–Riemann 方程成立.
反之, 上述计算表明我们只要取
F′(z0)=∂x∂f(x0,y0)+i∂x∂g(x0,y0)作为极限
z→z0limz−z0F(z)−F(z0)的取值即可.
我们现在研究 Cauchy–Riemann 方程的的基本解, 关于基本解这个概念我们后面会进一步阐明. 我们考虑在 C 上几乎处处定义的映射C−{0}, z↦z1.我们把这个复值函数就记作 z−1 或者 z1. 由于 ∣∣z1∣∣⩽r1, 其中, r 为平面上的极坐标系中的半径函数, 根据换元积分公式, 我们很容易看出z1∈Lloc1(C).
将 z1 视作是 C=R2 上的分布. 那么, 在分布的意义下, 我们有∂(πz1)=D′δ0.特别地, 对于任意的 z0∈C, 我们有∂(π(z−z0)1)=δz0.用偏微分微分方程的语言来描述, πz1 为算子 ∂ 的基本解.
在证明之前, 我们先陈述两个关于分布收敛的基本事实, 它们的证明留作作业 (请参考第 2 次作业) :
• | 假设 {fp}p⩾1 是 Ω 上的一列局部可积的函数, f∈Lloc1(Ω). 如果对任意的紧集 K⊂Ω, 我们有p→∞limfp∣∣K=L1(K)f∣∣K,那么, 作为分布, 我们有p→∞limfp=D′f. |
• | 假设 {up}p⩾1 是 Ω 上分布的序列, u∈D′(Ω). 如果p→∞limup=D′u.那么, 对任意的多重指标 α, 在分布的意义下, 我们有p→∞lim∂αup=D′∂αu. |
另外, 我们还有
• | 对于任意的 f∈C∞(Ω) 和 u∈D′(Ω), 对任意的 k⩽n, 我们有∂k(f⋅u)=D′∂kf⋅u+f⋅∂ku. |
证明也留作习题.
证明. 为此, 我们定义
fε(z)=⎩⎨⎧πz1, ∣z∣⩾ε;πε2z, ∣z∣<ε.所以,
gε(z)=fε(z)−πz1=1∣z∣<ε(z)⋅(πε2z∣z∣2−ε2).当
ε→0 时,
gε 是逐点 (几乎处处) 收敛到
0 的; 我们还可以用
π∣z∣21∣z∣⩽1(z) 作为
ε⩽1 时的控制函数. 所以, 根据 Lebesgue 控制收敛定理, 我们有
gε(z)⟶L10, ε→0.所以,
fε⟶D′πz1, ε→0.从而,
∂fε⟶D′∂(πz1), ε→0.现在我们来计算
∂fε. 我们把
fε 写作
fε(z)=πε2z⋅1∣z∣⩽ε(z)+πz1⋅1∣z∣⩾ε(z).根据分布意义下的 Stokes 公式, 我们有
∂fε(z)=πε21⋅1∣z∣⩽ε(z)−πε2z⋅dσ∣z∣=ε+πz1⋅dσ∣z∣=ε=πε21⋅1∣z∣⩽ε(z).其中, 我们用到了
∂(z)=1, ∂(z1)=0,z=0.我们把这两个计算留作习题. 我们现在对
∂fε(z)=πε211∣z∣⩽ε(z),取极限. 我们发现这就是
ε21h(ε1), h(z)=π11∣z∣⩽1(z),的极限, 其中
h∈L1(R2) 并且积分为
1. 根据我们之前已经学过的例子, 我们有
πε211∣z∣⩽ε(z)⟶D′δ0, ε→0.这就证明了引理.
这个公式是所谓的 Cauchy 积分公式在一个点处的情况. 为了叙述 Cauchy 积分公式, 我们先讨论一下复变量 (复值) 函数在曲线上的积分.
假定 γ:[0,a]→C 是一个分段光滑 (C1) 的连续曲线, 也就是说, 存在 t0=0<t1<t2<⋯<tn−1<a=tn, 使得 γ:(tk−1,tk)→C 是 C1 的. 在每段上面, 我们有s↦γ(s)=x(s)+iy(s).对于复函数 F(z), 我们定义∫γF(z)dz=k=1∑n∫tk−1tkF(γ(s))γ′(s)ds=k=1∑n(∫tk−1tkF(γ(s))x′(s)ds+i∫tk−1tkF(γ(s))y′(s)ds).我们要区分一下这个定义与我们上学期定义的曲线积分的关系. 实际上, 如果我们假设 γ′(s)=0, 有∫γF(z)dσ=∫γF(γ(s))∣γ′(s)∣ds.所以, 这里的区别在于考虑的曲线的方向: 比如说, 我们考虑另一条曲线 γ−1, 它是 γ 沿着反方向来走, 即γ−1:[0,a]→C, s↦γ(a−s).那么, ∫γF(z)dz=−∫γ−1F(z)dz.
作为例子, 我们来计算2πi1∫∣z∣=r0zkdz, k∈Z,r0>0.我们用[0,2π]→C, ϑ↦r0eiϑ,来参数化 ∣z∣=r0, 所以, 我们有2πi1∫∣z∣=r0zkdz=2πi1∫02π(r0)keikϑ(−r0sinϑ+r0icosϑ)dϑ=2π1∫02π(r0)k+1ei(kϑ+1)dϑ={1, 0, k=−1;k=−1.
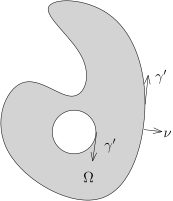
我们可以对一个复函数用 Green 公式. 假定紧集 Ω 的边界是 γ, 其中我们是按照逆时针或者顺时针来标记其方向的, 但是要求区域要在这个切向量的左手边.
我们用弧长参数来参数化边界曲线. 我们有
∫Ω∂F(z)dxdy=21∫Ω∂x∂F(z)+∂y∂(iF(z))散度形式dxdy=21∫γ(F,iF)⋅外法向量(−i)(γx′+iγy′)dσ=21∫γ(F,iF)⋅(γy′,−γx′)dσ=2i1∫γF(z)dz.我们现在来证明 Cauchy 积分公式:
假设 Ω⊂C 是开集, K⊂Ω 是有界带边区域 (特别地, K 是紧的) , 其边界 γ=∂K 是 C1 曲线 (可以有多个连通分支) . F(z) 是 Ω 上的复解析函数. 那么, 对于 z0∈K˚ (K 的内部) , 我们有F(z0)=2πi1∫γz−z0F(z)dz.
证明. 选取一个支集在
z0 附近小邻域中的试验函数
θ, 要求在
θ 在
z0 的一个邻域内恒为
1 并且
supp(θ)⊂K˚. 利用上面的 Stokes 公式, 我们有
2i1∫γz−z0(1−θ(z))F(z)dz=∫K∂((1−θ(z))z−z0F(z))dxdy.由于
supp(θ)⊂K˚, 所以
1−θ 在
γ 上恒等于
1, 从而
2i1∫γz−z0F(z)dz=∫K∂((1−θ(z))z−z0F(z))dxdy.根据 Leibniz 公式, 我们就有
2i1∫γz−z0F(z)dz=∫K−∂θ(z)z−z0F(z)dxdy+∫K(1−θ(z))≡0∂(z−z0F(z))dxdy=−⟨z−z0F(z),∂θ(z)⟩=⟨∂(z−z0F(z)),θ(z)⟩=π⟨F(z0)δz0,θ(z)⟩=πF(z0).这就给出了证明.