8.3. 两个总体下的区间估计

在某些场合下, 我们可能会面临对两个总体进行比较的问题. 例如, 为了验证一种新的食品添加剂在某个剂量下是否具有毒性, 我们可能需要进行如下形式的试验: 首先将足够多的小白鼠分成实验组和对照组, 让实验组的小白鼠按照一定剂量服用该食品添加剂, 而让对照组的小白鼠服用一定剂量的安慰剂, 随后统计并比较两组小白鼠的某项生化指标. 在这个例子中, 我们就可以用两个总体 $X_1$ 与 $X_2$ 分别代表服用食品添加剂小鼠与服用安慰剂小鼠的某项生化指标, 而实验组的检测结果即可看作是总体 $X_1$ 的一组样本 $X_{1,1},\dots ,X_{1,n_1}$, 对照组的检测结果则可看作是总体 $Y$ 的一组样本 $X_{2,1},\dots ,X_{2,n_2}$.

本节中, 我们将对一些两个总体下的区间估计问题进行介绍. 如无特别说明, 我们用 $X_1$, $X_2$ 表示两个总体, 用 $X_{k,1},\dots ,X_{k,n_k}$ 表示总体 $X_k$ 的一组样本 (其中 $k=1,2$), 且假定 $X_{1,1},\dots ,X_{1,n_1},X_{2,1},\dots ,X_{2,n_2}$ 相互独立. 此外, 用如下符号$${\overline{X}}_k=\frac{1}{n_k}\sum _{i=1}^n{X}_{k,i},S_k^2=\frac{1}{n_k-1}\sum _{i=1}^n(X_{k,i}-{\overline{X}}_k),k=1,2$$来表示两组样本 $X_{1,1},\dots ,X_{1,n_1}$ 与 $X_{2,1},\dots ,X_{2,n_2}$ 各自的样本均值和样本方差.

两个正态总体下期望之差的估计

设总体 $X_1$ 服从正态分布 $\mathcal{N}({\mu }_1,{\sigma }_1^2)$, 而总体 $X_2$ 服从正态分布 $\mathcal{N}({\mu }_2,{\sigma }_2^2)$, 我们希望对两个总体的期望的差 ${\mu }_1-{\mu }_2$ 进行区间估计. 我们根据两个总体方差信息的知晓程度, 讨论两种容易求解的情况.

两总体方差均已知的情况. 设两个总体的方差 ${\sigma }_1^2,{\sigma }_2^2$ 均已知. 我们构造枢轴量$$\frac{{\overline{X}}_1-{\overline{X}}_2-({\mu }_1-{\mu }_2)}{\sqrt{{\sigma }_1^2/n_1+{\sigma }_2^2/n_2}}.$$利用例 4.3.9 所给出的两个独立的正态随机变量线性组合后概率分布的结论, 不难验证上述枢轴量服从标准正态分布 $\mathcal{N}(0,1)$. 由此可得$${\mathbb{P}}_{{\mu }_1,{\mu }_2}\left(-z_{\alpha /2}\le \frac{{\overline{X}}_1-{\overline{X}}_2-({\mu }_1-{\mu }_2)}{\sqrt{{\sigma }_1^2/n_1+{\sigma }_2^2/n_2}}\le z_{\alpha /2}\right)=1-\alpha .$$对上式进行等价变换可得$${\mathbb{P}}_{{\mu }_1,{\mu }_2}\left(\left[{\overline{X}}_1-{\overline{X}}_2-z_{\alpha /2}\sqrt{\frac{{\sigma }_1^2}{n_1}+\frac{{\sigma }_2^2}{n_2}},{\overline{X}}_1-{\overline{X}}_2+z_{\alpha /2}\sqrt{\frac{{\sigma }_1^2}{n_1}+\frac{{\sigma }_2^2}{n_2}}\right]\ni {\mu }_1-{\mu }_2\right)=1-\alpha .$$故 ${\mu }_1-{\mu }_2$ 的一个置信水平为 $1-\alpha$ 的置信区间为$$\left[{\overline{X}}_1-{\overline{X}}_2-z_{\alpha /2}\sqrt{\frac{{\sigma }_1^2}{n_1}+\frac{{\sigma }_2^2}{n_2}},{\overline{X}}_1-{\overline{X}}_2+z_{\alpha /2}\sqrt{\frac{{\sigma }_1^2}{n_1}+\frac{{\sigma }_2^2}{n_2}}\right].$$

两总体方差未知, 但已知它们相等的情况. 设 ${\sigma }_1^2,{\sigma }_2^2$ 均未知, 但已知 ${\sigma }_1^2={\sigma }_2^2$; 习惯上我们用 ${\sigma }^2$ 来表示这两个方差共同的值. 此时我们考虑构造一个服从 $t$ 分布的枢轴量. 为此, 我们先利用定理 6.2.3 得到如下结论:

1.	${\overline{X}}_1-{\overline{X}}_2-({\mu }_1-{\mu }_2)$, $S_1^2$ 以及 $S_2^2$ 这三个随机变量相互独立;
2.	$(n_k-1)S_k^2/{\sigma }_k^2\sim {\chi }^2(n_k-1)$, 其中 $k=1,2$. 由于 ${\sigma }_1^2={\sigma }_2^2={\sigma }^2$, 这进一步意味着$$\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{{\sigma }^2}$$服从自由度为 $n_1+n_2-2$ 的 ${\chi }^2$ 分布.

而由于 ${\overline{X}}_1-{\overline{X}}_2-({\mu }_1-{\mu }_2)\sim \mathcal{N}(0,{\sigma }^2(1/n_1+1/n_2))$, 接下来我们利用定理 6.2.4, 即可看出$$\frac{\left[{\overline{X}}_1-{\overline{X}}_2-({\mu }_1-{\mu }_2)\right]/\sqrt{{\sigma }^2(1/n_1+1/n_2)}}{\sqrt{\left[(n_1-1)S_1^2+(n_2-1)S_2^2\right]/\left({\sigma }^2(n_1+n_2-2)\right)}}=\frac{{\overline{X}}_1-{\overline{X}}_2-({\mu }_1-{\mu }_2)}{\sqrt{S_p^2\left(1/n_1+1/n_2\right)}}$$(8.3.1)服从自由度为 $n_1+n_2-2$ 的 $t$ 分布, 其中我们记$$S_p^2=\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2};$$统计量 $S_p^2$ 通常被称为合并方差 (pooled variance). 故式 (8.3.1) 给出了一个枢轴量. 利用 $t$ 分布的上分位数, 可得$$\mathbb{P}\left(-t_{\alpha /2}(n_1+n_2-2)\le \frac{{\overline{X}}_1-{\overline{X}}_2-({\mu }_1-{\mu }_2)}{\sqrt{S_p^2\left(1/n_1+1/n_2\right)}}\le t_{\alpha /2}(n_1+n_2-2)\right)=1-\alpha .$$由此可算得 ${\mu }_1-{\mu }_2$ 的一个置信水平为 $1-\alpha$ 的置信区间为$$\left[{\overline{X}}_1-{\overline{X}}_2-t_{\alpha /2}(n_1+n_2-2)\sqrt{S_p^2\left(\frac{1}{n_1}+\frac{1}{n_2}\right)},{\overline{X}}_1-{\overline{X}}_2+t_{\alpha /2}(n_1+n_2-2)\sqrt{S_p^2\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}\right].$$

两个正态总体下方差之比的估计

设总体 $X_1$ 服从正态分布 $\mathcal{N}({\mu }_1,{\sigma }_1^2)$, 而总体 $X_2$ 服从正态分布 $\mathcal{N}({\mu }_2,{\sigma }_2^2)$, 其中 ${\mu }_1,{\mu }_2,{\sigma }_1,{\sigma }_2$ 均为未知参数. 我们希望对两个总体的方差之比 ${\sigma }_1^2/{\sigma }_2^2$ 进行区间估计.

既然是对方差之比进行区间估计, 那么一个自然的想法是利用关于样本方差之比的推论 6.2.6 来设计枢轴量. 由推论 6.2.6 可得, $$\frac{S_1^2/{\sigma }_1^2}{S_2^2/{\sigma }_2^2}\sim F(n_1-1,n_2-1).$$利用 $F$ 分布的上分位数, 可得 (见图 1)$$\mathbb{P}\left(F_{1-\alpha /2}(n_1-1,n_2-1)\le \frac{S_1^2/{\sigma }_1^2}{S_2^2/{\sigma }_2^2}\le F_{\alpha /2}(n_1-1,n_2-1)\right)=1-\alpha .$$对上式括号中的不等式进行等价变换, 易得 ${\sigma }_1^2/{\sigma }_2^2$ 的一个置信水平为 $1-\alpha$ 的置信区间为$$\left[\frac{S_1^2/S_2^2}{F_{\alpha /2}(n_1-1,n_2-1)},\frac{S_1^2/S_2^2}{F_{1-\alpha /2}(n_1-1,n_2-1)}\right],$$或者根据 $F$ 分布上分位数的性质 (6.2.1) 式, 也可表示为$$\left[\frac{S_1^2}{S_2^2}{F}_{1-\alpha /2}(n_2-1,n_1-1),\frac{S_1^2}{S_2^2}{F}_{\alpha /2}(n_2-1,n_1-1)\right].$$

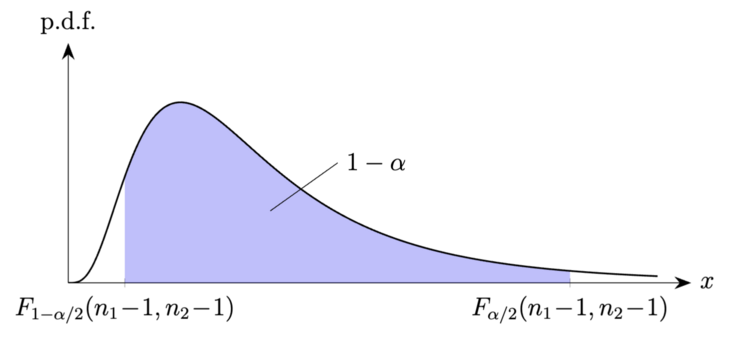图 1. 两个正态总体下, 利用枢轴量 $\frac{S_1^2/{\sigma }_1^2}{S_2^2/{\sigma }_2^2}$ 求解方差之比的置信区间.

大样本情形下两个伯努利总体比例之差的区间估计

设 $X_1$ 服从参数为 $p_1$ 的伯努利分布, 而 $X_2$ 服从参数为 $p_2$ 的伯努利分布, 其中 $p_1,p_2\in [0,1]$ 均未知. 在两个样本的容量 $n_1,n_2$ 均足够大的情形下, 我们可以利用中心极限定理, 得到$$\frac{{\overline{X}}_1-p_1}{\sqrt{p_1(1-p_1)/n_1}}\text{与}\frac{{\overline{X}}_2-p_2}{\sqrt{p_2(1-p_2)/n_2}}$$均近似服从标准正态分布 $\mathcal{N}(0,1)$, 且二者互相独立. 进一步可知$$\frac{{\overline{X}}_1-{\overline{X}}_2-(p_1-p_2)}{\sqrt{p_1(1-p_1)/n_1+p_2(1-p_2)/n_2}}$$近似服从标准正态分布 $\mathcal{N}(0,1)$. 但需要注意的是, 上式给出的随机变量并非 $X_1,\dots ,X_n$ 与 $p_1-p_2$ 的函数, 故不能把它作为对 $p_1-p_2$ 进行区间估计的枢轴变量. 为此, 我们考虑到在大样本情形下, 有如下近似成立: $$\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}\approx \sqrt{\frac{{\overline{X}}_1(1-{\overline{X}}_1)}{n_1}+\frac{{\overline{X}}_2(1-{\overline{X}}_2)}{n_2}},$$因而可以认为$$\frac{{\overline{X}}_1-{\overline{X}}_2-(p_1-p_2)}{\sqrt{{\overline{X}}_1(1-{\overline{X}}_1)/n_1+{\overline{X}}_2(1-{\overline{X}}_2)/n_2}}$$也近似服从标准正态分布, 且由于该随机变量是 $X_1,\dots ,X_n$ 与 $p_1-p_2$ 的函数, 故可以把它作为近似的枢轴量用于求解置信区间. 利用标准正态分布的分位数, 可得$$\mathbb{P}\left(-z_{\alpha /2}\le \frac{{\overline{X}}_1-{\overline{X}}_2-(p_1-p_2)}{\sqrt{{\overline{X}}_1(1-{\overline{X}}_1)/n_1+{\overline{X}}_2(1-{\overline{X}}_2)/n_2}}\le z_{\alpha /2}\right)\approx 1-\alpha .$$上式括号中的不等式可等价变形为$$\underline{\Delta }\le p_1-p_2\le \overline{\Delta },$$其中$$\begin{array}{rl}\underline{\Delta }=& {\overline{X}}_1-{\overline{X}}_2-z_{\alpha /2}\sqrt{\frac{{\overline{X}}_1(1-{\overline{X}}_1)}{n_1}+\frac{{\overline{X}}_2(1-{\overline{X}}_2)}{n_2}},\\ \overline{\Delta }=& {\overline{X}}_1-{\overline{X}}_2+z_{\alpha /2}\sqrt{\frac{{\overline{X}}_1(1-{\overline{X}}_1)}{n_1}+\frac{{\overline{X}}_2(1-{\overline{X}}_2)}{n_2}}.\end{array}$$由此可得, $p_1-p_2$ 的置信水平为 $1-\alpha$ 的置信区间可近似取为 $[\underline{\Delta },\overline{\Delta }]$.