道路连通分支 π 0 令 X ∈ Top
•
映射 γ : I → X γ ( 0 ) γ ( 1 )
•
记号 γ − 1 γ ( 1 ) γ ( 0 ) γ − 1 ( t ) = γ ( 1 − t )
•
记号 i x 0 : I → X x 0 ∈ X
图 1. 拓扑空间 X γ γ − 1
我们来定义 X x 0 ∼ x 1 ⟺ 存在从 x 0 到 x 1 的一条道路 . π 0 ( X ) = X / ∼ X
π 0 h Top Set
若 X , Y π 0 ( X ) = π 0 ( Y )
证明. 对函子
π 0 : h Top → Set 应用命题
1.19 .
道路范畴/基本群胚 令 γ : I → X γ [ γ ] = { γ ~ : I → X ∣ γ ≃ γ ~ rel ∂ I = { 0 , 1 }} .
图 2. 在一个道路类中, F : γ ≃ γ ~ rel ∂ I
[ γ ] γ
γ 1 , γ 2 : I → X γ 1 ( 1 ) = γ 2 ( 0 )
γ 2 ⋆ γ 1 ( t ) = { γ 1 ( 2 t ) γ 2 ( 2 t − 1 ) 0 ≤ t ≤ 1/2 1/2 ≤ t ≤ 1 , γ 2 ⋆ γ 1 : I → X
图 3. 道路的合成
设 f 1 , f 2 , g 1 , g 2 f i ( 1 ) = g i ( 0 ) [ f 1 ] = [ f 2 ] [ g 1 ] = [ g 2 ] [ g 1 ⋆ f 1 ] = [ g 2 ⋆ f 2 ] .
证明. 下图描述了证明, 其中
F : f 1 ≃ f 2 而
G : g 1 ≃ g 2 .
我们于是知道 ⋆ [ g ⋆ f ] : = [ g ] ⋆ [ f ] .
f , g , h : I → X f ( 1 ) = g ( 0 ) g ( 1 ) = h ( 0 ) ( [ h ] ⋆ [ g ] ) ⋆ [ f ] = [ h ] ⋆ ( [ g ] ⋆ [ f ] ) .
令 γ : I → X γ ( 0 ) = x 0 γ ( 1 ) = x 1 [ γ ] ⋆ [ i x 0 ] = [ γ ] = [ i x 1 ] ⋆ [ γ ] .
证明. 我们只证明第一个等式, 它由下图推出: □
令 X ∈ Top Π 1 ( X )
•
Obj ( Π 1 ( X )) = X
•
Hom Π 1 ( X ) ( x 0 , x 1 ) = 从 x 0 到 x 1 的道路类
•
1 x 0 = [ i x 0 ]
前面的命题推出 Π 1 ( X ) Π 1 ( X ) X 道路范畴 或基本群胚 .
群胚 所有态射可逆的小范畴称为群胚 . 所有的群胚构成一个范畴 Grpd
一个群 G G
•
Obj ( G ) = { ⋆ }
•
Hom G ( ⋆ , ⋆ ) = G
于是我们得到一个全忠实函子 Grp → Grpd
回忆 γ − 1 γ
γ : I → X γ ( 0 ) = x 0 γ ( 1 ) = x 1 [ γ ] ⋆ [ γ − 1 ] = [ 1 x 1 ] , and [ γ − 1 ] ⋆ [ γ ] = [ 1 x 0 ] . Π 1 ( X ) Π 1 ( X ) 是群胚.
证明. 令
γ u : I → X 使得
γ u ( t ) = γ ( t u ) , 其中
u ∈ I 任意. 下面的图给出同伦
γ − 1 ⋆ γ ≃ 1 x 0 的构造:
用下面的图, 为定理 2.12 γ − 1 ⋆ γ ≃ 1 x 0
令 C Π 0 ( C ) = Obj ( C ) / ∼ , A ∼ B C ∃ f : A → B Π 0 ( C ) C → Π 0 ( C ) Grpd Set Π 0 ( C ) C 道路连通的 .
令 C A ∈ Obj ( C ) Aut C ( A ) := Hom C ( A , A ) .
任意的 f : A → B Ad f : Aut C ( A ) g → Aut C ( B ) → f ∘ g ∘ f − 1 . Ad f 将 A 映到 A B g g f f − 1
这便自然定义了函子C → Grp 定义为 A ↦ Aut C ( A ) , f ↦ Ad f . Π 1 ( X ) → Grp .
令 x 0 ∈ X π 1 ( X , x 0 ) := Aut Π 1 ( X ) ( x 0 ) ( X , x 0 ) 基本群 .
X x 0 , x 1 ∈ X π 1 ( X , x 0 ) ≅ π 1 ( X , x 1 ) .
证明. 考虑上述的函子
Π 1 ( X ) → Grp . 因为
X 道路连通,
Π 1 ( X ) 是群胚, 任两点
x 0 和
x 1 在
Π 1 ( X ) 中同构. 由命题
1.19 ,
π 1 ( X , x 0 ) ≅ π 1 ( X , x 1 ) .
鉴于定理
2.17 , 在道路连通的情况下, 我们有时就简单地将
X 的基本群记为
π 1 ( X ) 而不点明基点.
令 f : X → Y Π 1 ( f ) : Π 1 ( X ) → Π 1 ( Y ) 定义为 x ↦ f ( x ) , [ γ ] ↦ [ f ∘ γ ] .
Π 1 Π 1 : Top → Grpd , X Π 1 ( X )
f , g : X → Y F : X × I → Y τ x = [ F ∣ x × I ] ∈ Hom Π 1 ( Y ) ( f ( x ) , g ( x )) , x ∈ X τ F := { τ x : x ∈ X } τ F : Π 1 ( f ) ⟹ Π 1 ( g ) .
证明. 令
r : I → X ,
r ( 0 ) = x 0 ,
r ( 1 ) = x 1 . 我们要证明在道路类的层次上, 下图交换:
合成
F ∘ ( r × I ) 给出如下的同伦:
这导出
[ g ∘ r ] ⋆ [ τ x 0 ] = [ τ x 1 ] ⋆ [ f ∘ r ] , 即证.
这个命题可以总结为如下的图表.Top Grpd X Π 1 ( X ) 同伦 F 自然变换 τ F Y Π 1 ( Y ) Π 1 f g Π 1 ( f ) Π 1 ( g )
令 f : X → Y Π 1 ( f ) : Π 1 ( X ) → Π 1 ( Y ) π 1 ( X , x 0 ) ≅ π 1 ( Y , f ( x 0 )) .
证明. 令
g : Y → X 代表
f 在
h Top 中的逆. 将
Π 1 应用到同伦
f ∘ g ≃ 1 Y 和
g ∘ f ≃ 1 X 上, 我们就找到了从
Π 1 ( f ) ∘ Π 1 ( g ) 和
Π 1 ( g ) ∘ Π 1 ( f ) 到恒同函子的自然变换. 因为
Π 1 ( X ) 和
Π 1 ( Y ) 是群胚, 这些自然变换一定是自然同构. 于是得到第一个命题. 第二个命题则是
1.26 的推论.
令 X , Y ∈ Top Π 1 ( X × Y ) ≅ Π 1 ( X ) × Π 1 ( Y ) . x 0 ∈ X , y 0 ∈ Y π 1 ( X × Y , x 0 × y 0 ) ≅ π 1 ( X , x 0 ) × π 1 ( Y , y 0 ) .
对于点 X = pt π 1 ( pt ) = 0 R n π 1 ( R n ) = 0 , ∀ n ≥ 0.
我们将在 3 6 π 1 ( S 1 ) = Z , 且 π 1 ( S n ) = 0 , ∀ n > 1.
令 T n = ( S 1 ) n n π 1 ( T n ) = Z n .
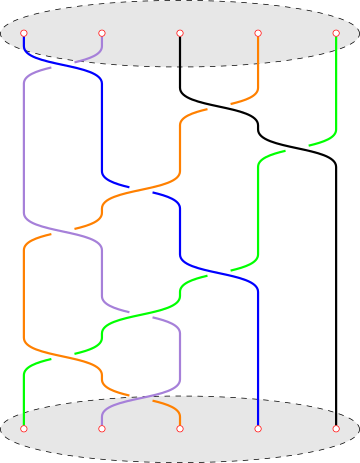
n Br n n Br n = ⟨ b 1 , … , b n − 1 ∣ b i b j b i = b j b i b j b j b i = b i b j ∀∣ j − i ∣ = 1 , ∀ ∣ j − i ∣ > 1 ⟩ .
令 X ∈ Top X n X n Conf n ( X ) := { x = ( x 1 , … , x n ) ∈ X n ∣ x i = x j , ∀ i = j } . S n Conf n ( X ) S n × Conf n ( X ) ( σ , x ) ⟶ Conf n ( X ) ⟼ σ ( x ) = ( x σ ( 1 ) , x σ ( 2 ) , … , x σ ( n ) ) . X UConf n ( X ) = Conf n ( X ) / S n .
一个经典的结果是Br n ≅ π 1 ( UConf n ( R 2 )) ≅ π 1 ( UConf n ( D 2 )) .
更进一步, 这个 (基本) 群中的元素可以这样直观地看成 R 3 n R 2 Z 1 , ⋯ , Z n n Ψ = ( ψ 1 , … , ψ n ) ψ i ψ i : [ 0 , 1 ] → R 2 × I ⊂ R 3
•
ψ i ( 0 ) = Z i × { 0 }
•
ψ i ( 1 ) = Z σ ( i ) × { 1 } σ { 1 , … , n }
•
对任意 0 ≤ t ≤ 1 { ψ 1 ( t ) , … , ψ n ( t )} R 2 × { t }
几何辫的乘法用和道路 (在基本群中) 的乘法一样的方式给出. R 3 4 b 1 b 3 b 4 b 2 − 1 b 1 b 3 b 2 − 1 b 1 b 2 − 1 .
图 4. 经典的辫子
n 英文 n th
道路范畴 • 英文 path category
基本群胚 • 英文 fundamental groupoid
群胚 • 英文 groupoid
道路连通 • 英文 path connected
基本群 • 英文 fundamental group
鞭群 • 英文 braid group